海量时空轨迹的梯形带相似聚类
2018-03-27孙卫真林秋慧赵秋香
孙卫真,林秋慧,向 勇,赵秋香
1(首都师范大学 信息工程学院 计算机科学与技术系,北京 100048) 2(清华大学 计算机科学与技术系 网络所,北京 100084) 3(山东省 济宁市第一中学 高中数学组,山东 济宁 272000)
1 引 言
由于GPS设备的逐渐普及,基于位置服务[1]的广泛应用等,位置信息的获取变得愈加便捷.毫无疑问,这些数据的汇集将是海量的、个体连续的.个体连续的位置信息数据按照采样时刻连接而成后,可以得到该运动对象的时空轨迹.海量的时空轨迹背后隐藏的信息带动了轨迹挖掘的发展,目前的应用范围涵盖了包括交通监管、人类行为、动物迁徙、自然风暴预测等等[2].因此,分析并聚类实时的海量时空轨迹数据,获取典型的轨迹模式是非常有必要的.
然而,存储开销大、计算强度高、聚类几何特征保留不完整等问题,是海量时空轨迹数据的聚类目前所面临的主要挑战[3,4].目前国内外在轨迹聚类方面的研究中,主要有以下几个方向[6]:基于数据的稀疏度、基于空间划分、基于兴趣点以及基于轨迹的几何特征等.其中,基于数据的稀疏度的方法,属于数据挖掘的通用方法[7],但时间与空间复杂度都很高,不适用于海量时空轨迹的聚类;而基于空间划分的方法,计算量相对较小,一般会结合LCSS方法并在明确的应用场景下使用[6,8];基于兴趣点划分的方法准确度较差,且在兴趣点较多的地区,轨迹的校准与划分将存在一定困难[9].而基于轨迹几何特征方法的文献则相对较少,其中,文献[10]提出了一种基于结构相似度的轨迹聚类算法,与轨迹的几何特征有一定的的相关性,但其对原始轨迹的要求较高.Lee等人[2]在2007年提出了一种新的基于几何形状的聚类拟合轨迹的方法,其方法解决了复杂轨迹之间的比较问题,但是对轨迹进行了近似描述,从而造成了轨迹的局部几何特征丢失.
此外,实时海量的时空轨迹数据的聚类分析,还需考虑聚类的存储与计算压力的问题[11],目前已有的解决时效性问题的主要方法集中在对聚类前的轨迹数据进行简化[12,13].现有的轨迹数据的简化算法主要分为两种[12]:一是局部轨迹数据简化,二是整体轨迹数据简化.局部轨迹数据的简化主要针对待处理点,综合分析并处理与邻域点间的简化关系,如距离阈值的过滤方法等[14].而整体的轨迹简化大致包括如下四种经典的算法[3]:自顶向下(Top-Down,TD)[15]、自下而上、滑动窗口、开放窗口(Opening Window,OW).其中,OW算法的窗口大小是动态调整的,该算法适用于实时的流式轨迹数据.然而经典的OW算法在特殊轨迹的处理上并不理想,其一,其简化后的轨迹保留的拐角信息点过少[12],导致减少了一些更准确的轨迹行进可能;其二,轨迹点过于密集时,其动态滑动窗口过长,从而明显增加计算量.余超等在文章[16]中提出的角度可变的滑动窗口算法,能够在转角较大的情况下保留部分拐角轨迹点.而TD算法对于处理有规律且比较直的密集轨迹点时,效率非常高,可以弥补OW算法的不足.其经典方法有道格拉斯普克(Douglas-Peucher,DP)[4,13]算法,比较常见的有针对既定路线或网格的轨迹简化[5,17].
以上的文献分析可以看出,实时海量时空轨迹聚类的首要问题是由于几何特征丢失导致的聚类不准确性[10].聚类的准确性取决于相似性度量方法,现有的轨迹间相似性度量方法主要集中在轨迹间距离上.如图1所示,轨迹1、2与轨迹1、3的欧氏距离和是相同的,即相似度一致,然而轨迹1与轨迹2的几何形状特征明显不一致,这无法达到相似性度量的准确性预期.此外,简化应当能够保留必要的轨迹数据特征,而现有的轨迹数据简化方法不能直接应用到这一场景中.因此,有必要设计一种海量时空轨迹聚类的算法,用以保留必要的轨迹几何特征,并兼顾时效性和准确性的问题.
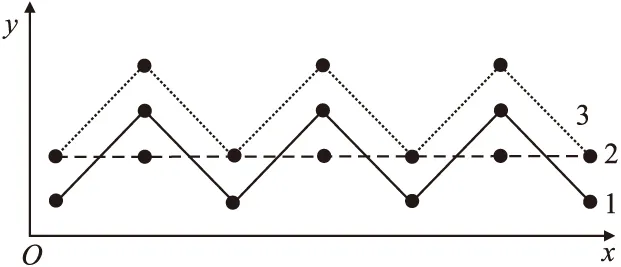
图1 欧式距离相似度不准确性Fig.1 Inaccuracy of Euclidean distance similarity
针对海量时空轨迹的聚类,本文将贯彻时效性和准确性两大原则进行阐述分析.首先,为减小计算量和存储开销,本文引入了一种综合的轨迹简化策略,不仅充分考虑了轨迹的时间和空间要素,更加入了轨迹的形状特征因素.着眼于简化后的时空轨迹数据的几何特征,在前期的工作[18]中,我们结合计算几何的方法对轨迹进行扩展,选择了计算复杂度较低的轨迹梯形带,定义了轨迹间的相似性度量方法.该方法可以在多项式时间内计算轨迹范围,并判断在不同时间跨度上的轨迹间相似性,在此基础上,本文提出了海量时空轨迹的梯形带相似聚类算法.该方法利用线性线段落在轨迹形成的梯形范围内长度和本身长度的比值定义相似,在充分考虑轨迹几何特征的条件下,能够较为快速地获取时空轨迹的有效聚类结果.最后,经海量真实时空轨迹数据测试集(北京市2010年04月06日出租车数据)测试,本文方法能快速并合理保留细节特征地进行轨迹数据简化,准确有效地聚类同类轨迹并获取合理的轨迹模式.
2 轨迹相似性度量
相似性度量作为轨迹聚类的标准,给出的定义越契合实际,轨迹聚类的效果也越好.此前的工作中,为减小计算量,采用梯形带的方式简化了时空轨迹带[18].众所周知,聚类后的轨迹簇一般是分区域的,那些区域可大可小,形状不一.分在一个簇中的轨迹定义为相似的,相对于簇而言,这些轨迹是细小的.将轨迹簇类比于时空轨迹的梯形带,那么相似于该梯形带的轨迹也是细小的.因此,如图2所示,假设存在一个轨迹梯形带,令其他的轨迹均与轨迹带的中心轨迹进行相似度匹配,即可得到有效的轨迹聚类,其直观的度量标准为落在轨迹带中轨迹长度与轨迹原长度的比值.
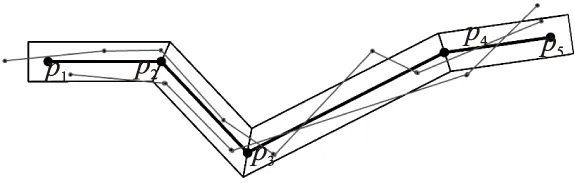
图2 轨迹的梯形带扩展及相似性示意Fig.2 Trapezoidal belt of trajectory and similarity diagram
经过以上论证,为更准确的描述轨迹间相似性,本文将在已有研究的基础上,增加轨迹的几何特征因素,提出如下的轨迹相似性度量模型.
2.1 时空轨迹的定义
运动对象的时空轨迹是由一系列采样点,按照采样时刻的顺序连接而成的.传统的轨迹描述方法[19]主要利用二维空间坐标,其缺点是,轨迹分类局限性较大,且无法非常准确地描述一条轨迹.为提高轨迹聚类的有效性,参考文献[20]的做法,利用运动物体的特定编号、空间坐标、速度、方向等信息共同描述一条轨迹.
定义1.时空轨迹:一条时空轨迹可以表示为
Tr={(id,pi)|pi=(xi,yi,ti,vi,di),i=1,2,…,n}
(1)
其中,id表示轨迹Tr的特定编号,也即唯一标识,pi表示轨迹的第个采样点,n表示轨迹的采样点个数,(xi,yi)表示第i个采样点的二维空间坐标,(ti,vi,di)分别表示轨迹Tr在第i个采样点位置的时间信息、速度信息和方向信息.
定义2.原始轨迹:原始数据经过实时预处理后,按轨迹编号形成了一条条连续的轨迹.
(2)
定义3.轨迹模式:代表一组轨迹,初始聚类时,取原始轨迹中的一条经准确简化而成.在类中轨迹达到一定量时,拟合这类轨迹并简化,得到新的更合理的轨迹模式.

(3)
其中simiID为与该轨迹模式相似的原始轨迹的相似度similarity与oriID对的集合,初始为Ø.
2.2 时空轨迹梯形带
定义4.时空轨迹梯形带:表示如下

(4)
2.3 轨迹相交判断
避免完全不可能相交的两轨迹段进行轨迹相似计算,能够有效减少计算量,通过判定构成轨迹段的基于坐标系的最小矩形是否相交,能够粗略地判定轨迹段是否相交.
定义5.相交粗判:设有两点(xn,yn)、(xn+!,yn+1),则两点构成的基于坐标系的最小矩形为R,可以表示成R((xmin,ymin),(xmax,ymax)),其中(xmin,ymin)是R左下角点,(xmax,ymax)是的右上角点.


(5)

2.4 轨迹相交长度
1978年,Cyrus&Beck[21]提出了一种判断直线与凸多边形相交测试的算法—Cyrus&Beck裁剪算法(以下简称CB算法),其算法的复杂度为O(n).如图3所示,除重合外,线段与多边形相交主要有以下4种情况.
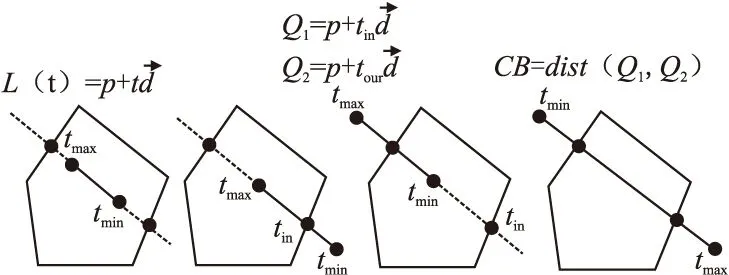
图3 CB算法求解相交长度Fig.3 CB algorithm for intersection length
本文采用了增加重合情况的算法,用以计算轨迹段与梯形带的相似长度.

LenCB(Apexi,pjpj+1)
(6)
2.5 轨迹的相似性计算
为衡量时空轨迹的几何相似性,在判定轨迹段与轨迹带的相交情况后,利用轨迹段落在轨迹带中的长度与轨迹段自身原长的比值,可以描述为轨迹的几何相似性.
定义7.基于梯形带的轨迹相似性:原始轨迹Tro与轨迹模式Trm产生的梯形带Tp进行匹配,有轨迹段RIi-j=1.说明两者可能相交,并可能产生轨迹段相似长度.则轨迹Tro与Trm的扩展梯形带Tp的基于梯形带的轨迹相似度(Trapezoidal Belt Based Similarity, TBST)可以表示为:
(7)
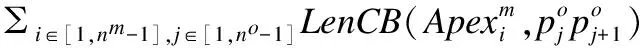
3 轨迹间的相似聚类算法
为实时处理海量真实的时空轨迹数据,通过对数据进行预处理,完成了清洁可用数据的获取.为了保证实时海量时空轨迹聚类的时效性和准确性,针对轨迹数据存在大量密集点和直线轨迹点等特征,提出了海量时空轨迹的梯形带相似聚类算法(Feature Preserved-Trapezoidal Belt,FP-TB),它包含2个阶段.其一是综合的特征保留简化算法,它在保证能够保留轨迹几何特征的条件下,尽可能地进行数据存储量的压缩,并以不增加时间开销为目的.其二是时空轨迹的梯形带相似聚类算法,它在更优的时间内获取更具价值的轨迹模式.下面将进行更为具体的描述.
3.1 必要的轨迹简化策略
基于海量实时时空轨迹的时效性和准确性的需求,本文在前述内容的基础上,为较快压缩数据量、保留细节特征时尽量减少锐角并快速处理较长的密集轨迹点,在轨迹数据简化方面,制定整体轨迹数据简化为主,局部轨迹数据简化为辅的综合轨迹压缩算法,以达到快速并合理保留轨迹特征地进行轨迹数据压缩.
其中,局部邻域点简化(Neighborhood Points Compression,NPC)的核心思想在于,综合分析待处理点与邻域点,较快压缩数据量.而整体轨迹数据简化的算法又包含有两种,一种是带锐角限制的开窗算法(Angle Limited Opening Window,ALOW),用于整体的动态简化并保留一些较为特殊的轨迹局部特征;另一种是针对拥有大量较为笔直的轨迹点,利用DP算法直接进行轨迹简化.实时动态简化以NPC算法为第一道关卡,ALOW算法为主要的简化方法,在点阈值达到一定程度时再触发DP算法,三者相辅相成.以下是详细的算法描述.
算法1.综合的特征保留简化算法(Feature Preserved Simplification,FP).
输入:原始轨迹Tro,局部简化阈值SUBSIMPTHR,整体简化阈值SIMPTHR,长直轨迹点阈值PTTHR
输出:简化后的轨迹Trosimp
算法步骤:
1)initialize(SUBSIMPTHR,SIMPTHR,PTTHR);//初始简化阈值
2)copyInfo(Tro,Trosimp)//复制轨迹基本信息到简化轨迹中
3)addp1toTrosimp//将轨迹起始点放入简化轨迹中
4)for(next= 1;next≤n;next++){
5)for(i= 1;i≤n-next;i++){ //NPC算法
6)if(Dist(pnext,pnext+i)>SUBSIMPTHR){
7) delete {pnext+1,pnext+i-1} fromTro;
8)break;
9) }
10) }
11) countDP = 0;//用于触发DP算法的flag
12)for(j= 1;j≤n-next-i;j++){//ALOW算法
13) LPDist=
Dist(Line(pnext,pnext+i+j),pnext+i+K),K∈[0,j);
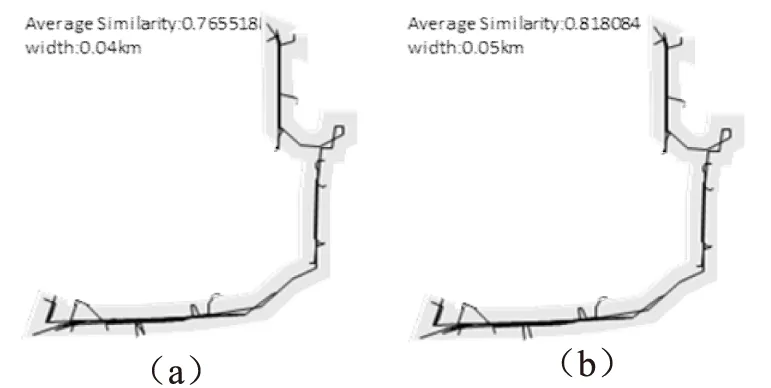
14)if(LPDist 15) countDP++; 16)else{ 17) Kmax=MAX(LPDist);//当有距离超过SIMPTHR时,选择距离最大的浮动点 18)Qobt=FIRSTAngle(∠pbeforepnextpnext+i+Q>90°) ‖MAXAngle(∠pbeforepnextpnext+i+Q>90°), Q∈[Kmax,0] //注意向前浮动 19) addpnext+i+QobttoTrosimp;//浮动点放入简化轨迹 20)next=next+i+Qobt,countDP=0; 21) } 22)if(countDP ≥PTTHR){ 23) //超过轨迹点阈值PTTHR,触发DP算法. 24) addpnext+i+jtoTrosimp; 25) dpLine(pnext,pnext+i+j); 26) countDP=0,next=next+i+j; 27) } 28) } 29)} 30)returnTrosimp; 算法1是一个特征保留的轨迹简化算法,它首先选择从待简化的原始轨迹Tro中,取第一个点作为简化轨迹Trosimp的起始点,其后续进入的每一个点,均先与前一个简化后的点进行NPC算法,再按照如下的ALOW算法简化轨迹段. 前一条简化后的轨迹段末端点作为起始点,从该点开始处理后面连续的n(n>=3)个点,第n个点设为浮动点:过起始点和浮动点做一条直线,分别计算中间n-2个点到直线的距离LPDist,若所有距离均小于距离阈值,则下一个数据点设为浮动点,计数;否则,选取与直线距离最大的点作为浮动点,进行“浮动点前移”:从该浮动点向前到起始点的下一点,依次作为浮动点计算三个点之间的夹角,利用函数FIRSTAngle选取浮动点,该浮动点是第一个和起始点间的轨迹段与前一条轨迹段成钝角的点,将该浮动点加入到简化轨迹Trosimp中,并成为下一个起始点;若所有两轨迹段间的夹角都不大于90°,则利用函数MAXAngle选取与前一条轨迹段成最大角的浮动点加入到简化轨迹Trosimp中,作为下一次循环的起始点. 当在ALOW算法简化过程中的计数超过阈值时,触发DP算法函数dpLine,将所有当前未处理的点取出,并将首尾两点存入简化轨迹Trosimp中,连接这两点,计算中间所有点到该线的距离,若超过阈值,则将距离最大的点存入Trosimp中;连接首尾两点,得到两条直线,重复前述步骤,直到所有点到直线的距离均不超过阈值为止. 该算法得到的简化轨迹,通过NPC算法减小了OW算法的繁复计算压力,利用DP算法的优势缓解了OW算法在处理长直轨迹点时的计算压力,锐角特性的加入,则使得最终得到的简化轨迹保留了一定的细节特征,能有效地应用于实际场景中,同时为后续的聚类分析减小了较大的工作量. 本文的相似性度量标准,基于轨迹的几何特征,在扩展简化后的轨迹模式Trm为梯形带后,采用原始轨迹Tro落在轨迹模式Trm中的轨迹相似长度和,与原始轨迹Tro的长度比值来进行定义.这种方法,弥补了欧氏距离对轨迹几何特征的忽略,解决了采用多边形重合面积比定义相似性的不稳定问题.基于此,轨迹便能够得到较好的聚类,并能够得到更能代表聚类轨迹特征的轨迹模式.具体算法如下: 算法2.海量时空轨迹的梯形带相似聚类算法(Trapezoidal Belt Based Clustering,TB). 输入:原始轨迹集合I={Troi,i=1,2,…,k},其中原始轨迹为实时增加的;轨迹模式集合Q={Trmi,i=1,2,…,s},初始为空集Ø,随聚类的进行而增长;相关参数:轨迹带宽度WIDTH,相似度阈值SIMILARTHR 输出:轨迹模式类集合Q 算法步骤: 1)initialize(WIDTH,SIMILARTHR);//初始梯形带宽度、相似度阈值 2)Q=Ø;//初始化轨迹模式类集合Q为空集 3)for(eachTrokin theI){ //遍历集合的原始轨迹 4)if(Q==Ø){ 5) createNewTrm(Tro,Trm);//生成第一条轨迹模式Trm 6) addTrmtoQ;//将Trm加入到轨迹模式类集合Q中 7) } 8)else{ 9) similarflag=false; 10)for(eachTrmsin theQ){ //遍历集合Q的轨迹模式 11) creatApex(Trms,WIDTH);//依据轨迹带宽度生成轨迹模式梯形带 13)if(TBBS>SIMILARTHR){ 14) add(TBBS,ido)tosimiID;//维护当前Trm的simiID 15) similarflag=true; 16) } 17) } 18)if(similarflag ==false){ 19) createNewTrm(Tro,Trm); 20) addTrmtoQ;//将Trm加入到轨迹模式类集合Q中 21) } 22) } 23)} 算法2在初始时,初始化轨迹模式集合Q为空集,相关参数的梯形带宽度WIDTH和相似度阈值SIMILARTHR.对所有在原始轨迹集合I中的所有原始轨迹,与所有在轨迹模式集合Q中的每一条轨迹模式进行相似度计算.首先生成简化后的轨迹模式梯形带,采用前述的相似性度量模型,计算两轨迹间的相似度TBBS的值.继而判断当相似度的值大于相似度阈值SIMILARTHR时,认为该原始轨迹Tro与当前Trm相似,维护当前Trm的simiID集合,从而达到聚类效果.最后,若当前轨迹模式集合Q中没有任何一条轨迹模式Trm与该原始轨迹Tro相似的话,依据该原始轨迹Tro生成一条轨迹模式Trm并参与后续计算. 从此处可以看出,轨迹模式所含数据点越多,则轨迹模式段越多,轨迹模式所对应的梯形带中所含梯形越多,这样,计算原始轨迹在梯形带内的长度时,计算量就会越大,所以,轨迹模式是简化后的轨迹,而且,简化后的轨迹做轨迹模式与原始轨迹计算的相似度和未简化前的轨迹做轨迹模式与原始轨迹计算相似度,两者相似度相差不大,而前者的计算量则较后者大大减小了. 在给出具体算法的基础上,分析算法的时间复杂度是很有必要的.通过时间复杂度的分析,能够进一步的改进和优化算法的结构,以达到更加实时高效的目的. 算法1是一个综合特征保留的轨迹简化算法,为了追求最好的效率,可能需要反复执行,反复对轨迹点进行简化,进而减少轨迹点的数量,对m条轨迹,其执行次数为O(m).对每个被保留的轨迹点而言,需要在其他剩余的轨迹点中,寻找下一个被保留点,候选的轨迹点共有O(n)个.因此,每次执行的算法时间复杂度最差为O(n2),最好的情况为O(log2n),其中n表示轨迹集合中轨迹的数量. 算法2是海量时空轨迹的梯形带相似聚类算法,针对算法1产生的轨迹集合形成的原始轨迹,其轨迹的平均长度为O(n-1),对于每个轨迹点,需要在m条轨迹模式中进行相似度拟合,因此,算法2的时间复杂度为O(n-1)O(m). 其中,算法2由于原始轨迹的个数是实时增加的,其执行的效率主要取决于在聚类过程中形成的轨迹模式条数,当轨迹模式较少,其执行效率较高,反之,执行效率降低.目前本算法对待轨迹模式的增加主要取决于轨迹间相似度的阈值,后续将会基于此进行有效的改进. 以上分析可知,本文提出的FP-TB算法,在计算轨迹相似性时,增加了特征保留的轨迹点简化,减少了大量的轨迹点,其对较为笔直和密集轨迹点的简化大大提高了轨迹的简化执行效率,利用这些简化后的轨迹点进行相似度计算,充分减少了计算量.增加的轨迹几何形状的因素,则使得本算法所得的轨迹聚类结果更加准确. 在实验部分,采用真实数据扩展的数据集对算法的可用性进行分析.其中真实数据集为2010年04月06日的30382520条北京市出租车数据,通过过滤得到较为清洁的数据,并在此基础上利用空车与重车标志位分割轨迹,共得到可用轨迹35380条.使用该数据集的优势在于,它包含大量的轨迹信息,包括轨迹的速度、角度、时间、位置信息、轨迹标识、类别信息等,并且这些轨迹信息都是真实的,其轨迹出现的情况均为真实应用环境的情形,能够验证本文所述方法的真实有效性. 实验的硬件环境为:服务器端Ubuntu 14.04,内存2.00GB,数据库端为Windows 7系统,安装Oracle DB 11g,算法实现代码为C++,并均在服务器终端进行测试运行. 4.1.1 轨迹简化算法的几何特征保留情况 本文提出的特征保留的轨迹简化算法FP,其主要目标是在不影响轨迹简化速率的基础下,尽可能多的保留原始轨迹的有效特征.以较小的空间开销,保留更多的轨迹特征,其轨迹的可用性越高,反之亦然.在该算法中,有三个阈值需要确定,其中仅有SIMPTHR阈值是与简化效果密切相关的距离阈值. 由于其距离阈值所针对的点均为地图上的点,而就中国的情况而言,纬度范围从3°51′N至53°33′N,跨度较大,因此不适合在任意纬度指定固定的阈值.为了获取更为合理的阈值,在指定阈值时,以千米km为单位,指定阈值为αkm,则不同纬度的纬度阈值由以下公式(8)换算得到: (8) 下面的实验结果展现了在不同α值决定的SIMPTHR阈值下,本文算法FP与OW算法所得的简化轨迹的对比结果. 图4-图6中虚线均代表原始轨迹,共17个点,左图的实线为OW算法简化后的轨迹,右图实线则是本文算法FP简化后的轨迹.如图5所示,在本文的算法中,在保留了原始轨迹中的第8个点之后,若利用OW算法则下一个点为第10个点(即左图算法中保留的第6个点),由于第8个点和前一个被保留点所成的线段与第8、10个点所成的线段夹角为锐角,本文的算法利用“浮动点前移”,到第9个点(即右图中保留的第7个点),使得两者之间的夹角不是锐角.利用OW算法简化后的轨迹均含有1个锐角,而本文算法FP简化后的轨迹则不含锐角,且简化结果较为稳定. 图4 值为0.01km时OW与FP的简化效果Fig.4 Simplified results of OW and FP at α=0.01km 图5 值为0.02km时OW与FP的简化效果Fig.5 Simplified results of OW and FP at α=0.02km 图6 值为0.03km时OW与FP的简化效果Fig.6 Simplified results of OW and FP at α=0.03km 纵向比较图4、图5、图6可知,随着α值为0.01km、0.02km、0.03km,OW算法仅在值较小时才能保留原始轨迹的几何特征,而本文的算法FP,则能够在较大范围内均保持简化后的原始轨迹不失真.因此,本文算法FP较OW算法在实际应用中更为广泛. 4.1.2 执行时间比较 本文所使用的真实的出租车数据集中,存在个体连续的大量密集点、较长时间的直线行驶和部分大型立交桥的转弯行驶轨迹点,因此该简化算法主要基于以上的数据特征进行.描述的是,在使用α=0.02km时,OW、ALOW以及本文所述的FP简化算法,在压缩率及执行时间方面的表现.其中,简化的总点数W为3651685个点,形成了35380条原始轨迹. 结合上述实验一及表1数据可以得到,本文的综合特征保留算法FP的简化较OW算法能够保留更多原始轨迹的特征点,约多了6.75%.由于压缩率数值越大,压缩后的轨迹点所需的存储空间也越大,而本文算法FP较OW算法的整体压缩率增加了2.01%,存储空间开销随之增大,但这一比例属于存储的可接受范围.而对比ALOW算法,本文算法FP保留的轨迹点总数约少了2.36%,整体压缩率减少了0.77%.这一差异性是由于NPC及DP算法的简化造成的,而在执行时间减少诸多的情况下,这一情况基本可以忽略. 表1 各简化算法的压缩率及执行时间Table 1 Compression rate and execution time of each algorithm 通过观察表1可以发现,同等实验条件下,纯粹的ALOW算法由于其时间复杂性较OW算法高,其运行时间较OW算法高出约13%.对于海量的轨迹数据而言,时间上的开销是较难容忍的,因此需要对ALOW算法做进一步的改进.同样地,从上表也可以看出,本文的FP算法较OW算法的运行时间缩短了约25.82%,较纯粹的ALOW算法的执行时间缩短了约34.17%.这主要是因为NPC和DP算法有效地简化和压缩了这些增长的密集点和长直点,减小了ALOW以及OW算法的窗口,迭代次数随之减少,执行的时间自然减少.以上数据结果说明,增加了NPC算法和DP算法来进行执行效率上的改进结果是卓有成效的,达到了缩短执行时间的目的.因此本文提供的FP算法是有效的,且更为高效的. 4.2.1 梯形带宽度width对轨迹间相似的影响 本文提出的海量时空轨迹的梯形带相似聚类算法FP-TB中,阈值width是影响轨迹间相似判断的主要因素.下面是实验获取的某一类轨迹模式聚类的实验结果,展现了在不同的width取值下,本文算法FP-TB在同一类轨迹中,其平均相似度的变化. 图7 不同width下同类轨迹的平均相似度Fig.7 Average similarity of similar trajectories under different width 其中灰色底带表示轨迹模式,黑色线条表示与之相似的原始轨迹,阈值width是影响梯形带的半带宽. 图7(a)显示的是width=0.04km时,直线型轨迹的其中一类所有相似轨迹与轨迹模式的相似度平均值,其相似度平均值显示为0.765518.图7(b)显示的是width=0.05km时,直线型轨迹的其中一类所有相似轨迹与轨迹模式的相似度平均值,其相似度平均值显示为0.818084. 根据以上的实验结果,横向比较图7(a)与图7(b)不难得出,随着梯形半带宽width值的增大,其聚类的轨迹相似度平均值也随之增大,这说明类中的原始轨迹与轨迹模式的相似度也是增大的.这是符合前文所述相似性度量的结果,因此本文提供的FP-TB算法的相似性度量模型是行之有效的,且能准确有效的进行各类轨迹的聚类. 4.2.2 轨迹聚类结果及执行时间的比较分析 本文所用的真实出租车数据集,具有几何走势明显的特征,对于这类轨迹,其主要目标是尽可能保证轨迹聚类的准确性,并挖掘出有价值的轨迹模式信息.本文从35380条原始轨迹中进行挖掘,其获取的轨迹模式较多,下面将举例给出直线型轨迹模式和环型轨迹模式的聚类结果,以验证聚类的有效性,其梯形带宽度width=0.05km,轨迹的相似度阈值SIMILARTHR=0.65. 图8 不同类型的轨迹聚类结果Fig.8 Clustering results of different types of trajectories 图8显示的是根据本文所给的相似性度量模型,对原始轨迹集合进行聚类后所得的不同类型的轨迹模式.图8(a)显示的是简单的直线型轨迹模式,其基本呈直线走势,表明了所有与该直线型轨迹模式相似的原始轨迹的平均相似度为0.716002.参照北京市地图可以发现,该轨迹模式表示去往首都机场的机场线路径,说明在一天内,出租车去往首都机场的出行频次是较高的.图8(b)显示的则是环型轨迹模式,其走势为闭合的环线,图中表明所有与该环型轨迹模式相似的原始轨迹的平均相似度为0.770505.该轨迹模式表示由西便门桥、右安门桥、左安门桥、东便门桥所形成的环线,并去往双井桥附近.该区域有较多办公大楼,属于出租车司机的长期巡客区域,而双井附近有较多居民区,因此这一路线也是出租车经常会走的路线.这些轨迹模式均符合北京市的实际交通路况,说明本文的相似性度量模型对于各类轨迹模式均是有效的,而环型轨迹中保留的部分拐角信息,则是出于几何特征保留的考虑,由此可见,该聚类结果具备准确性. 此外,为定量比较聚类结果的执行时间,做了如下的几组实验来验证.其中轨迹模式A、B分别是轨迹模式A′、B′简化后的轨迹,与之聚类的原始轨迹为简化后的35380条出租车轨迹. 通过3.3的算法分析可知,本文所述的FP-TB算法其执行效率主要取决于轨迹模式的条数和单条轨迹模式的段数,其中轨迹模式条数主要由原始轨迹数据集决定.由表2可以看出,相同的轨迹在简化前后聚类所得的原始轨迹集合相差不大,其平均相似度的差别亦不大.而简化后的轨迹聚类时间大约都减少了50%,其中轨迹模式A较轨迹模式A′的聚类执行时间减少了52.2732%,轨迹模式B较轨迹模式B′的聚类执行时间减少了59.5798%. 表2 FP-TB算法与仅TB的聚类方法的执行时间比较Table 2 Comparison of the execution time between FP-TB and TB clustering method 综合在真实数据集上的实验测试可以发现,本文提出的FP-TB算法可用性较高,并在考虑到轨迹几何特征后,能够在不影响执行时间的情况下保留重要的原始轨迹特征.在此基础上,通过提出的相似性度量模型,计算原始轨迹落在轨迹模式梯形带内的长度总和与原始轨迹线段的长度和之比定义相似性,对原始轨迹进行准确聚类,这一聚类方法能够有效地对包括直线型与环型交叉等各类轨迹进行聚类,且执行时间较不经过处理直接进行聚类的方法快了近50%.因此,本文提出的FP-TB聚类算法是行之有效的. 本文在分析了海量时空轨迹数据的空间和时间特性后,考虑到已有的聚类算法在计算轨迹相似性时忽略了轨迹的几何特征对聚类结果的影响,导致获取的轨迹模式的部分重要细节特征失真的问题,针对出租车数据特征进行的轨迹挖掘,提出了FP-TB算法.第一阶段的FP算法从存储效率和保留简化后的细节特征出发,制定了整体简化为主,局部简化为辅的轨迹简化方案.第二阶段的TB算法,增加轨迹几何特征的影响因素,提出了一种新的相似性度量模型.并以此为主要依据并通过一定的相似度阈值准确筛选和挖掘相似的时空轨迹簇,进行海量时空轨迹的聚类分析.通过真实轨迹数据集上的实验可以看出,本文算法在保留更多的轨迹原始特征的情况下,能够准确有效地聚类同类轨迹以获取典型的出租车行驶轨迹;而对不同类的轨迹,其执行效率均有不同程度的提升,因此具有更高的实际意义. 在未来的研究工作中,我们将考虑在聚类过程中轨迹模式的局部增删与轨迹模式本身的动态调整,以获取更切合实际的轨迹模式,减小计算开销. [1] Gruteser M,Grunwald D.Anonymous usage of location-based services through spatial and temporal cloaking[C].Proceedings of the 1st International Conference on Mobile Systems,Applications and Services,ACM,2003:31-42. [2] Lee J G,Han J,Whang K Y.Trajectory clustering:a partition-and-group framework[C].ACM SIGMOD International Conference on Management of Data,ACM,2007:593-604. [3] Keogh E,Chu S,Hart D,et al.An online algorithm for segmenting time series[C].Data Mining,ICDM 2001,Proceedings IEEE International Conference on.IEEE,2001:289-296. [4] Meratnia N,Rolf A.Spatiotemporal compression techniques for moving point objects[C].International Conference on Extending Database Technology,Springer Berlin Heidelberg,2004:765-782. [5] Muckell J,Hwang J H,Lawson C T,et al.Algorithms for compressing GPS trajectory data:an empirical evaluation[C].Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems,ACM,2010:402-405. [6] Su H,Zheng K,Wang H,et al.Calibrating trajectory data for similarity-based analysis[C].Proceedings of the 2013 ACM SIGMOD International Conference on Management of Data,ACM,2013:833-844. [7] Simoudis E,Livezey B K,Kerber R G.Method for generating predictive models in a computer system:U.S.Patent 5,692,107[P].1997-11-25. [8] Su H,Zheng K,Huang J,et al.Calibrating trajectory data for spatio-temporal similarity analysis[J].The VLDB Journal,2015,24(1):93-116. [9] Fu Z,Hu W,Tan T.Similarity based vehicle trajectory clustering and anomaly detection[C].Image Processing,2005.ICIP,IEEE International Conference on.IEEE,2005,2:II-602. [10] Yuan Guan,Xia Shi-xiong,Zhang Lei,et al.Trajectory clustering algorithm based on structural similarity[J].Journal on Communications,2011,32(9):103-110. [11] Thuraisingham B,Khan L,Clifton C,et al.Dependable real-time data mining[C].Eighth IEEE International Symposium on Object-Oriented Real-Time Distributed Computing,IEEE Computer Society,2005:158-165. [12] Chen Y,Jiang K,Zheng Y,et al.Trajectory simplification method for location-based social networking services[C].Proceedings of the 2009 International Workshop on Location Based Social Networks,ACM,2009:33-40. [13] Douglas D H,Peucker T K.Algorithms for the reduction of the number of points required to represent a digitized line or its caricature[J].Cartographica:The International Journal for Geographic Information and Geovisualization,1973,10(2):112-122. [14] Tobler W R.Numerical map generalization,and notes on the analysis of geographical distributions[M].Department of Geography,University of Michigan,1966. [15] Hershberger J E,Snoeyink J.Speeding up the douglas-peucker line-simplification algorithm[M].University of British Columbia,Department of Computer Science,1992. [16] Yu Chao,Guo Qing,Xie Wen-jun,et al.A method of fast geomagnetic matching based on orientation alterable sliding window[J].Computer Simulation,2015,32(3):86-89. [17] Yu J,Chen G,Zhang X,et al.An improved Douglas-peucker algorithm aimed at simplifying natural shoreline into direction-line[C].Geoinformatics(GEOINFORMATICS),2013 21st International Conference on.IEEE,2013:1-5. [18] Zhao Qiu-xiang.Trajectory clustering algorithm based on trapezoid belt similarity measure[D].Beijing:Graduate School of Beijing Normal University,2015. [19] Hwang J R,Kang H Y,Li K J.Spatio-temporal similarity analysis between trajectories on road networks[C].International Conference on Conceptual Modeling,Springer Berlin Heidelberg,2005:280-289. [20] Hu Hong-yu.Research on methods for traffic event recognition based on video processing[D].Changchun:Jilin University,2010. [21] Cyrus M,Beck J.Generalized two-and three-dimensional clipping[J].Computers & Graphics,1978,3(1):23-28. 附中文参考文献: [10] 袁 冠,夏士雄,张 磊,等.基于结构相似度的轨迹聚类算法[J].通信学报,2011,32(9):103-110. [16] 余 超,郭 庆,谢文俊,等.地磁导航基于方向可变滑动窗口快速匹配方法[J].计算机仿真,2015,32(3):86-89. [18] 赵秋香.基于梯形带相似性度量的轨迹聚类算法[D].北京:北京师范大学,2015. [20] 胡宏宇.基于视频处理的交通事件识别方法研究[D].长春:吉林大学,2010.3.2 海量时空轨迹的梯形带相似聚类
3.3 算法时间复杂性分析
4 测试与性能分析
4.1 轨迹简化的实验结果

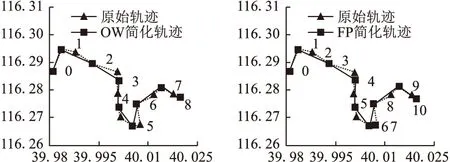
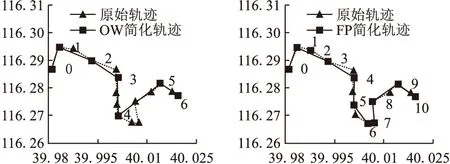

4.2 轨迹聚类的实验结果


5 结束语
