基于改进自适应无迹卡尔曼滤波的锂电池SOC估计＊

张周灿 谢长君 曹夏令 费亚龙 李小龙

（武汉理工大学，武汉 430070）

1 前言

电池荷电状态（State Of Charge，SOC）估计是电池管理系统的核心问题之一，而电池荷电状态受充放电电流、环境温度、循环次数等各种因素的影响，导致锂电池SOC值很难被直接测量。常用的SOC估计方法有以下几种：安时积分法[1]算法简单、易行、精度较高，但存在累计误差；开路电压法由于需要长时间静置，不适宜在线估计；神经网络算法[2]虽然精度高，但结构复杂，需要训练大量的数据。扩展卡尔曼滤波算法[3]（Extended Kalman Filter，EKF）是在电池荷电状态估计中广泛使用的算法之一，但其依赖精确的数学模型。在非线性处理上，其将非线性部分进行一阶泰勒展开，忽略了高阶项。因此在非线性很强情况下，容易使估算值严重偏离真实值。

无迹卡尔曼滤波（UKF）算法[4]、自适应卡尔曼滤波（AKF）算法[5，6]是当前的研究热点。但UKF算法应用前提是要精确获得系统过程噪声和观测噪声的统计特性，较为不便。AKF算法在线估计过程噪声和测量噪声的协方差矩阵，可提高系统状态的估计效果，但非线性较强时，滤波效果并不好。在两者基础上的自适应无迹卡尔曼滤波（AUKF）算法[7，8]结合概率统计知识，采用概率分布的思路处理非线性问题，是极具发展前景的非线性估计算法。本文将采用基于UT变换（Unscented Transformation，也称无迹变换）的自适应无迹卡尔曼滤波算法，基于锂电池2阶RC模型，对锂电池SOC进行估计。该算法是在传统UKF算法的基础上引入衰减因子与自适应调节因子，能够有效减少系统噪声的影响，提高算法滤波的稳定性。

2 锂电池状态模型的建立

文中选用磷酸铁锂电池进行试验。考虑到模型的准确度和计算复杂度，选择2阶RC电路模型作为锂电池SOC估计模型，电路模型如图1所示。2阶RC模型对电池的3种特性（欧姆极化、电化学极化和浓差极化）分别进行建模。模型中Uoc表示开路电压；Vo代表电池的端电压；Re是欧姆内阻；Rs与Cs环路描述电池电化学极化效应；Rs与Cp环路模拟电池内部的浓差极化效应；u为端电流。

根据图1所示电路图，以SOC、两电容上的电压Us、Up为状态变量，端电流u为输入变量，端电压Vo为输出变量。

图1 2阶RC等效电路模型

由基尔霍夫定律建立图1所示等效电路的状态空间模型并离散化，得到其离散状态空间模型：

u(k)为输入变量；T是系统采样周期。

3 开路电压与SOC关系的整定试验

为得到开路电压与SOC的关系，本试验采用中航锂电公司生产的额定容量为40A·h的磷酸铁锂电池，开路输出电压（标称电压）为3.2V。建立的试验测试装置主要由电源、采集板、显示器、锂电池、放电装置、霍尔电流传感器等组成。通过调节放电装置，使锂电池进行恒流放电试验。具体测试流程如下：先采用专用充电机将电池充满电，直至电池SOC为1（充满电状态），然后静置12h；在常温下，将电池的SOC值从1到0进行10等分的恒流脉冲放电试验，每次脉冲放电试验结束后将电池静置4h，并记录此时电池的开路电压值。脉冲放电电流为0.2C。

由上述试验数据可得开路电压Uoc与电池SOC的关系曲线如图2所示。由5阶曲线拟合可得它们之间的函数关系式如公式（2）所示：

图2 开路电压与SOC的关系

4 锂电池状态模型的参数辨识

本文采用递推最小二乘法来离线辨识锂电池模型参数，根据图1电池模型等效电路原理图，得到如下参数辨识原理式：

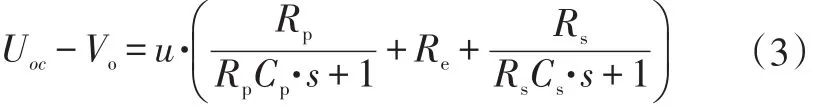
经过双线性变换处理得到如下方程式：

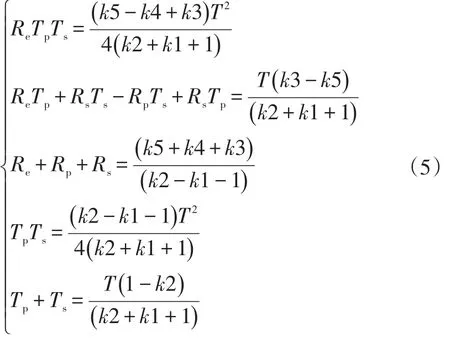
其中，T为采样周期，取状态变量：

得到最小二乘形式：

其中，e(k)是误差函数。最小二乘法递推计算公式如下：

初始值：θ(0)设置为0，协方差矩阵初始值P(0)=aI，a为很大的正数，I为5阶单位矩阵。

利用递推最小二乘法公式(7)估计出模型参数，然后采用公式(5)反推出模型的电容、电阻值：

5 基于AUKF的锂电池SOC估计

UKF算法本质上是通过线性插值方法，对非线性模型进行的高精度变换。当非线性程度较小时，可以削弱非线性误差的影响。其缺点是在非线性程度较强时，协方差更新时容易出现负定矩阵的情况。另外，UKF算法受初始值影响较大，系统噪声较为明显。在数据采集过程中噪声统计特性未知，会导致卡尔曼滤波法的估计精度降低，甚至会引起发散，导致滤波结果不稳定产生较大的误差。为了提高系统精度需要在传统UKF算法基础上加以改进。

5.1 UKF算法简介

按照卡尔曼的递推公式，根据新数据和前一状态的估计值，再借助系统本身的状态转移方程，得出当前时刻的状态估计值。锂电池的非线性系统离散状态空间方程为：

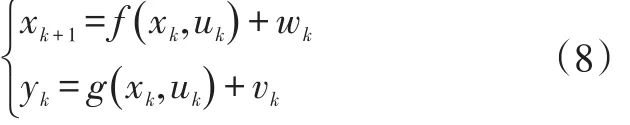
式中，f为非线性状态方程；g为非线性观测方程；Wk、Vk为随机变量x与观测变量y的高斯白噪声，其方差矩阵分别为 Qw和 Rv：

初始化X0=(SOC0，0，0 )设置为状态变量初始值，其方差估计P0：

根据状态变量的统计量xk-1及其协方差，状态变量的维数L=3；基于UT变换的自适应卡尔曼滤波估计锂电池SOC的算法步骤如下：

a.计算采样点

采用Sigma点对称采样策略，得到x点的Sigma点集，以及其对应的均值加权值和方差的加权值：

b.时间更新

根据状态方程式(1)计算状态更新:

计算预测状态值:

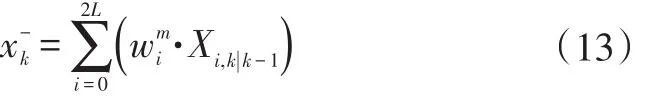
计算状态预测值的协方差:

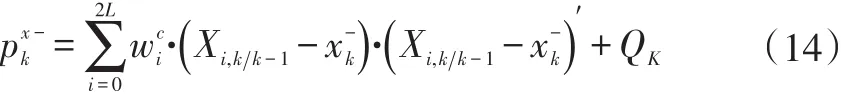
根据方程式(1)测量更新：

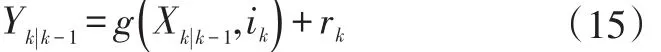
计算预测测量值：

计算测量估计yk的协方差：

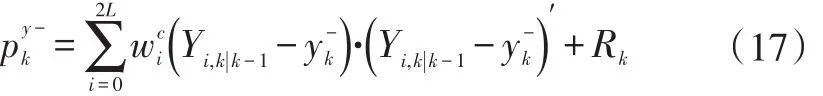
计算Xkk-1与Ykk-1的协方差：

c.测量更新

计算卡尔曼增益矩阵：

更新状态：

更新误差协方差：

5.2 AUKF算法

为了在非线性程度较强时能够有效提高电池SOC估算精度，降低初始值和系统噪声对滤波结果的影响，提高算法滤波的稳定性。在传统UKF算法基础上引入衰减因子与自适应调节因子，组成带有衰减记忆效应的无迹卡尔曼滤波器。由于系统噪声也会影响到滤波结果，因此引入自适应调节因子调节相关的协方差矩阵，在一定程度上可改变其在滤波过程的作用。

5.2.1 衰减因子

在UKF算法的基础之上引入衰减因子，组成带有衰减记忆效应的无迹卡尔曼滤波器。这种算法与传统UKF算法的主要不同之处是在公式（14）的基础上增加了衰减因子S，使得公式（14）转换成公式（22）：

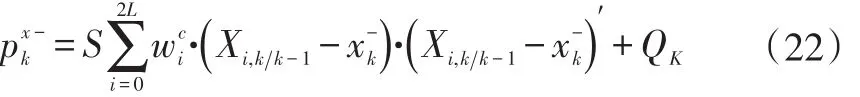
仿真结果表明，引入衰减因子后的算法带有衰减记忆效应，并且衰减因子S的选取对滤波结果有较大影响，滤波精度随着S的增大而减少，有时甚至会引起滤波发散。因此为有效提升滤波效果、提高系统稳定性，还需引入自适应调节因子。

5.2.2 自适应调节因子

传统UKF算法受初始值影响较大，此外，系统噪声同样也会影响滤波结果。因此，为了减少这些影响，自适应调节相关的协方差矩阵，可以在一定程度上改变其在滤波过程的作用。

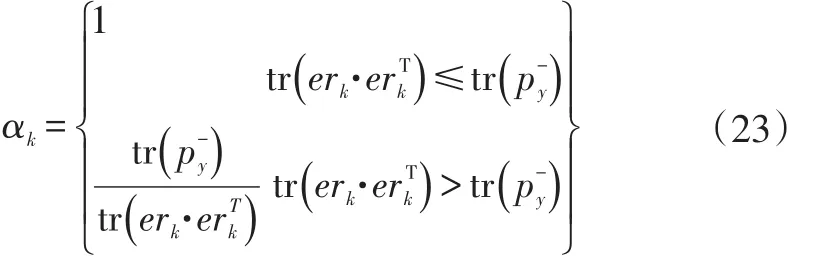
对协方差矩阵公式（17）、式（18）、式（21）进行修正得到：

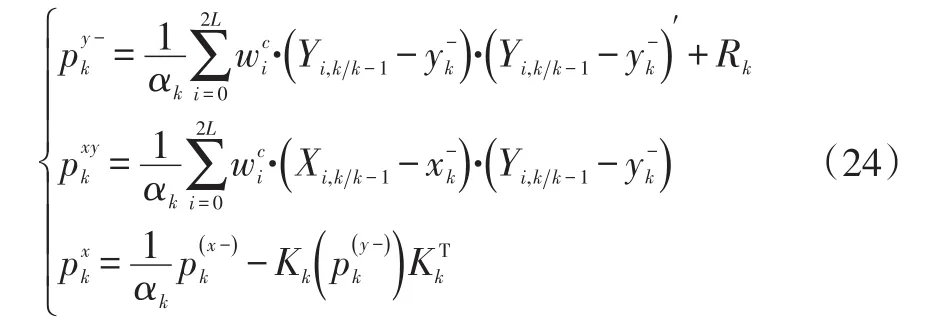
当UKF算法初始值存在误差或系统存在异常扰动时，自适应因子αk＜1，此时模型预测信息对最终滤波解的贡献小；当预测信息异常时，会很大，此时自适应因子接近于0，预测完全不起作用。下面通过具体工况试验验证引入衰减因子与自适应调节因子之后AUKF算法的优越性。

6 试验验证与结果分析

通过不同初始值情况下恒流放电工况试验，得到AUKF算法对SOC估计及误差曲线。在恒流脉冲充放电工况、美国城市循环工况（Urban Dynamometer Driv-ing Schedule，UDDS）两种工况试验下验证AUKF算法在传统UKF算法基础上引入衰减因子和自适应调节因子之后对滤波结果、SOC状态估计与估计误差的影响。

6.1 恒流放电工况试验

为了验证该算法不依赖初始值，对额定容量为单节40Ah的锂电池进行恒流充放电试验，试验环境温度为常温，放电累计时间为200s。放电试验前，对电池进行12h的充分静置，根据开路电压与电池SOC的对应关系获取初始SOC值。在试验过程中，实时采集电压电流值，采样频率为10次/s，对单体电池进行0.2C的恒流放电试验。通过测量得知，电池开路电压初始值为3.137V，电池SOC值为0.912，作为安时积分法的初始SOC值。

为验证SOC估算算法不依赖初始值的特性，假设SOC初始值偏离实际值，分别设定为0.8、0.6、0.96。采用AUKF算法来估计SOC值，并与安时积分法获得的参考值进行比较。试验数据曲线如图3、图4所示。从图3可知，不同的SOC初始值，基于AUKF算法均能快速收敛到参考值附近。从图4所示不同初始值下的估计误差曲线可知，在误差曲线后期，它们的估计误差均能保持在（-0.80%，0.80%）之间。由此可得，AUKF算法对初始值不敏感，且收敛速度较快。

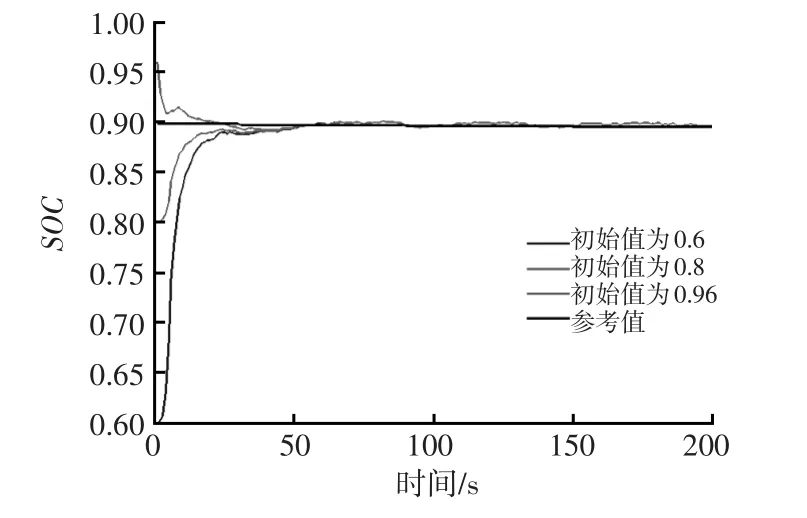
图3 不同SOC初始值下AUKF算法对锂电池SOC估计曲线

6.2 恒流脉冲充放电工况试验

为验证动态工况下算法的跟踪能力，选取自定义恒流脉冲充放电工况试验，电流工况数据如图5所示，负数代表放电，正数代表充电。分别采用安时积分、UKF算法与AUKF算法估算的SOC值曲线如图6所示，UKF和AUKF的估算误差曲线如图7所示。从图6中可知，这两种算法均能很好地跟踪SOC参考值的变化。从图7中可知，在初始阶段，基于AUKF算法的估计曲线更快收敛到参考值附近，且在后期，AUKF的误差比UKF的误差要小。两者均能保持在（-0.80%，0.80%），而传统UKF算法的误差最大会达到2%。

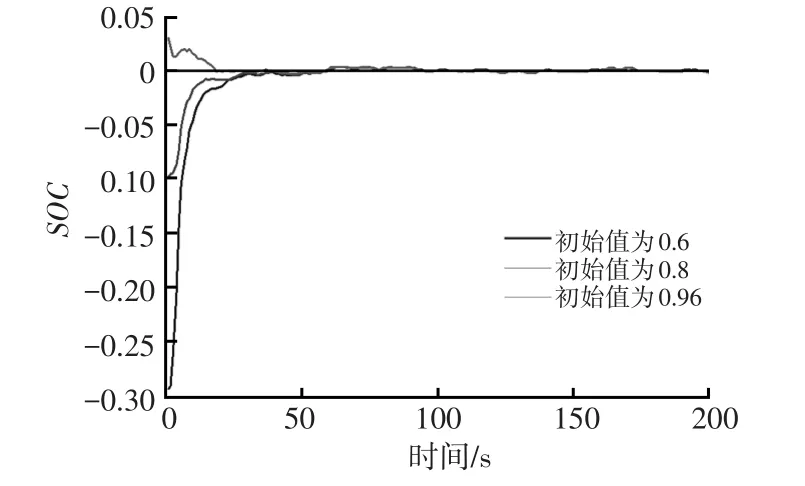
图4 不同SOC初始值下AUKF算法对锂电池SOC估计误差曲线

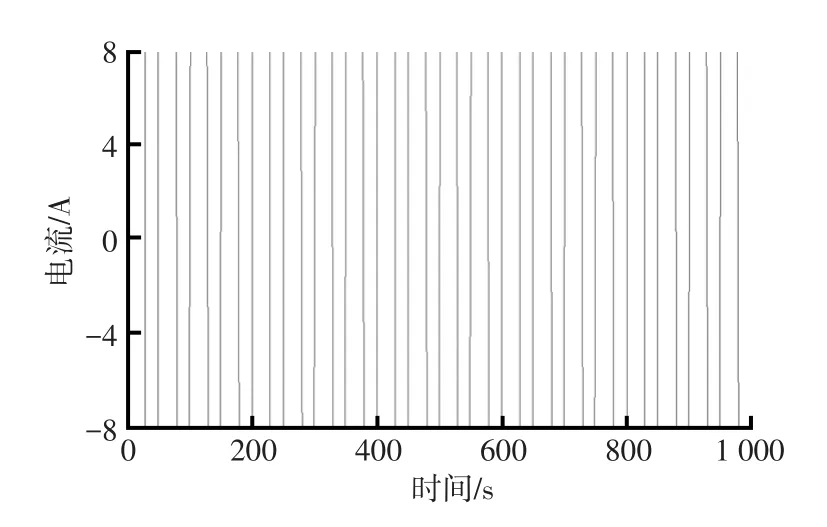
图5 恒流脉冲充放电电流工况数据

图6 恒流脉冲充放电的锂电池SOC估计

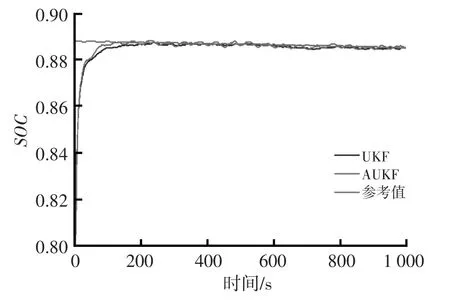
图7 恒流脉冲充放电的锂电池SOC估计误差

6.3 美国城市循环（UDDS）工况试验

为更好说明动态工况下算法的跟踪能力，选取美国城市循环工况（UDDS）验证试验。实时电压电流值的采样频率为10次/s。电流工况数据如图8所示，负数代表放电，正数代表充电。同样分别采用安时积分、UKF算法与AUKF算法估算的SOC值曲线如图9所示，UKF和AUKF的估算误差曲线如图10所示。

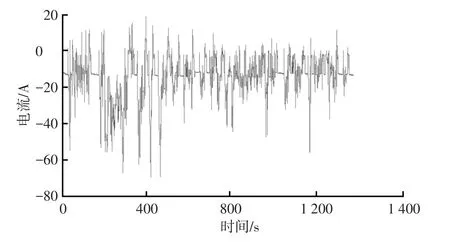
图8 UDDS工况下电流变化曲线

图9 UDDS工况下锂电池SOC值估计

图10 UDDS工况下锂电池SOC估计误差

仿真曲线表明，在UDDS与恒流脉冲充放电两种动态工况下AUKF曲线更加接近参考曲线，AUKF算法估算锂电池SOC的波动性较小。此工况验证试验结果与自定义恒流脉冲充放电工况试验结果相符。引入衰减因子与自适应调节因子之后的AUKF算法估算锂电池SOC的波动性比传统UKF算法小，系统噪声更低，自适应能力更强。

7 结束语

锂电池SOC值的在线估计是当前研究的热点和难点问题。文中提出了在UKF算法基础上引入衰减因子和自适应调节因子的AUKF算法，在上述多种动态实时工况中进行了对锂电池SOC估计的试验。试验结果证明，相比传统UKF算法，本文提出的基于AUKF算法对锂电池SOC估计具有更高精度及更好的跟踪性，提高了算法对初始值和系统噪声的鲁棒性，验证了AUKF算法在电池SOC估计方面实用性强、精度高和收敛快等优点。

[1]李申飞，易菊兰，琚小明.电池电量精确测量方法的研究与实现[J].计算机工程与应用，2009，45(17)：244-248.

[2]刘征宇，杨俊斌，张庆，等.基于QPSO-BP神经网络的锂电池SOC预测[J].电子测量与仪器学报，2013，27(3)：224-228.

[3]郭孔辉，付皓，丁海涛.基于扩展卡尔曼滤波的汽车质心侧偏角估计[J].汽车技术，2009(4)：1-3.

[4]沈艳霞，周园.基于无损卡尔曼滤波的锂离子电池组SOC估计[J].电源技术，2014，38(5)：828-831.

[5]张頔，马彦，柏庆文.基于自适应卡尔曼滤波的锂离子电池SOC估计[J].汽车技术，2011(8)：42-45.

[6]刘和平，许巧巧，胡银全，等.自适应卡尔曼滤波法磷酸铁锂动力电池剩余容量估计[J].重庆大学学报：自然科学版，2014，37(1)：68-74.

[7]魏克新，陈峭岩.基于自适应无迹卡尔曼滤波算法的锂离子动力电池状态估计[J].中国电机工程学报，2014，34(3)：445-452.

[8]胡志坤，刘斌，林勇，等.电池SOC的自适应平方根无迹卡尔曼滤波估计算法[J].电机与控制学报，2014，18(4)：111-116.