基于改进人工势场法的智能车辆超车路径规划研究＊

王树凤 张钧鑫 刘宗锋

（山东科技大学，青岛 266590）

1 前言

国内道路交通事故统计表明，由驾驶员自身造成的事故占总数的74%[1]，世界各国都试图通过智能车辆替代驾驶员完成驾驶任务，解决交通安全问题。其中，路径规划作为智能车辆研究的关键技术受到了广泛关注，而超车换道作为最基本的驾驶行为，是其重点和热点。

人工势场法作为机器人领域的常用路径规划算法，与A*启发式搜索法、遗传算法、蚁群算法、模糊算法等算法相比，算法简明、实时性良好、道路轨迹圆滑[2-4]，但其应用对象为机器人，未考虑车辆动力学、道路等约束条件，且易使被控对象陷入局部最小点。针对其应用到车辆实际路径规划，修彩靖等[5]提出在引力点函数中考虑道路约束和车辆约束，但该理论只针对简单的避障行为，没有考虑车辆具体驾驶行为；曹昊天等[6]提出在障碍车前、后添加引导势场的方法，建立弹性绳模型，实现超车换道，但该模型没有考虑车辆超车换道因素，换道结束后车辆不能及时回到原道路中心；翼杰等[7]构建了实际道路交通环境下的动态三维虚拟危险势场模型，但该模型只考虑了静态障碍物道路工况下的车辆避障驾驶；谭宝成[8]提出了优化人工势场圆形虚拟力场作用域模型，但该模型并没有考虑车辆动力学约束。

以上研究大多未考虑驾驶员的超车换道行为，对超车换道约束的考虑也不全面。本文以双车道车辆超车换道为研究对象，首先分析了驾驶员超车换道行为，考虑车辆动力学和道路等条件的约束，建立车辆超车换道最小安全距离模型，依据超车行为约束条件，提出障碍物斥力场的椭圆形作用域，引入基于前车工况的斥力系数、斥力调节因子和局部虚拟目标点，对传统人工势场法路径规划模型进行改进。在Simulink中搭建CarSim车辆模型和模型预测控制（Model Predictive Control，MPC）模型联合仿真平台，进行了超车换道轨迹跟踪验证。

2 双车道车辆超车模型

2.1 超车驾驶行为分析

为更好地规划智能车辆的超车轨迹，使之与驾驶员超车行为一致，需要分析驾驶员超车换道行为的特点，并将之融合到智能车辆超车换道的路径规划中。

车辆在双车道的道路上行驶时，如果前方车辆速度较低，影响通行效率，驾驶员产生超车需求。基于驾驶员的实际超车行为，对超车行为的产生到超车过程结束各车辆运动位置关系进行描述，如图1所示，超车车辆记为M1，被超障碍车辆记为M2，其他障碍车辆记为M3，超车行为过程如下：

a. 超车准备阶段：M1的速度大于前方车辆M2的速度，且相邻车道有安全的换道空间。

b. 超车过渡阶段：从行车道换至超车道，保证换道过程中具有安全的换道空间，即不与障碍车辆相撞，并且保证车辆安全稳定地换道。

c. 超车阶段：M1在超车道行驶一段距离，保证其超过M25～8m[9]。

d. 超车过渡阶段：从超车道换到行车道，保证换道过程中不与障碍车辆相撞，并保证车辆安全稳定。

e. 超车结束阶段：M1与M2之间保持安全车距。

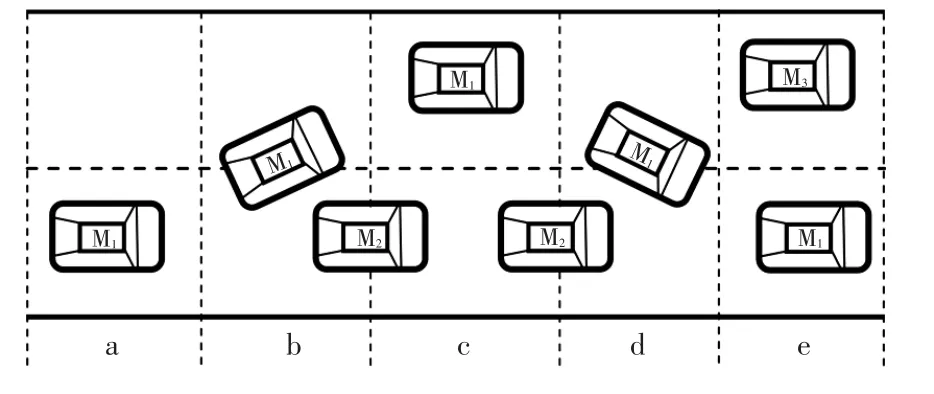
图1 超车过程车辆位置关系

2.2 安全换道空间的确定

从前文分析可知，换道过渡阶段最为复杂，安全换道空间的确定是成功换道的关键，不仅要保证不与障碍车辆相撞，还要满足车辆动力学、道路等条件的约束。

2.2.1 最小纵向安全避障距离

超车车辆M1在行驶过程中，当因前方车辆M2速度低而采取超车换道行为时，两者可能发生的碰撞为斜向碰撞，其临界状态如图2所示。C点为临界碰撞点，此时纵向距离D为最小纵向安全距离Dmin，如果两车在C点没有发生碰撞，则不会再发生碰撞。

保证两车不发生碰撞的条件[10]为：

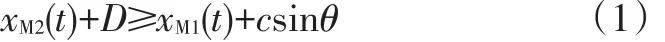
式中，xM1(t)、xM2(t)分别为车辆M1、M2经过时间t的纵向位移；c为车辆M1的宽度；θ为t时刻车辆M1车身与车道线之间的夹角；t∈[t0，tc+tadj]为时间；t0为车辆M1换道的初始时刻，可将其设为0；tadj为车辆M1在施加横向加速度前的调整时间；tc为车辆M1从施加横向加速度时刻至其到达碰撞临界点之间的时间。

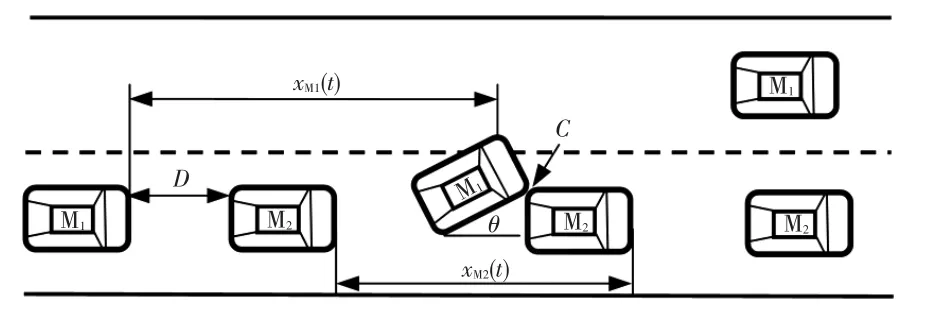
图2 车辆换道避障示意

进而由式（1）得到保障M1不与M2发生任何形式碰撞的最小纵向安全间距为：

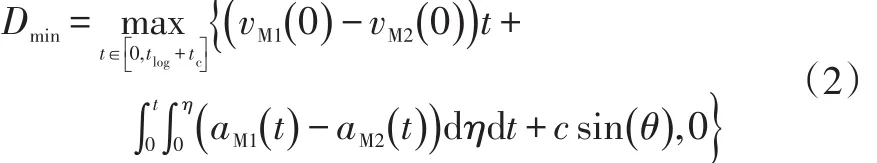
式中，vM1(0)、vM2(0)分别为换道开始时车辆M1和M2的纵向速度；aM1(t)、aM2(t)分别为换道过程中车辆M1和M2在t时刻的纵向加速度；η为时间。

由式（2）可知，影响最小纵向安全距离的参数较多，但因实际换道过程时间短，本文对超车换道过程作如下假设：超车换道过程中智能车辆以恒定纵向速度行驶；超车过程中前方车辆始终以恒定速度在车道中心线处行驶；超车道上其他车辆对超车换道没有影响。

2.2.2 换道超车约束条件

车辆路径规划不同于机器人控制，基于人工势场法所得到的车辆超车换道轨迹除具有障碍物的空间轨迹约束之外，还应具有道路条件的几何约束、车辆换道的安全距离约束和车辆自身的动力学约束。而车辆自身动力学约束非常复杂，如车辆位置连续要求轨迹曲线是连续的，横摆角连续要求轨迹曲线是一阶连续，而加速度约束则要求轨迹曲线二阶连续。为简化车辆动力学约束，本文设定车辆的运行工况均为匀速行驶。由此可得：

a.车辆轨迹约束：保证车辆之间不发生碰撞且不超出车道，即

特别地，当超车车辆M1处于超车道时：

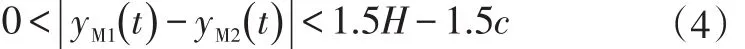
b. 车辆动力学约束：保证车辆安全、平稳地进行超车换道，即

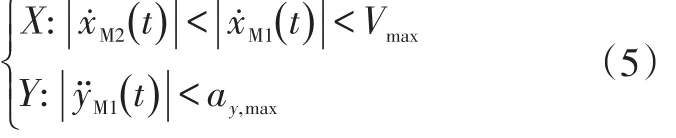
式中，yM1、yM2分别为M1、M2质心处横向位移；ay，max为车辆最大侧向加速度；Vmax为道路限速；H为目标车道与原车道几何中线间距；d为智能车辆与前车初始纵向距离。

文献[11]将变道过程中的车辆侧向加速度量化，考虑稳定性，约定侧向加速度小于限制级别，即ay≤0.67μg。其中，μ为路面附着系数，g为重力加速度。

3 基于人工势场法的超车路径规划

为使规划出的轨迹更贴合实际，结合上述超车行为分析理论，对传统人工势场法路径规划模型进行改进。

3.1 传统人工势场法

人工势场法是一种虚拟力方法，根据电荷间相互作用规律理论演变而来。其基本思想是，在被控对象运动环境中人为建立势场，其中障碍物为斥力场，目标点为引力场，分别对被控对象产生斥力和引力，引力和斥力构成的合力控制被控对象的运动方向，如图3所示。其中：

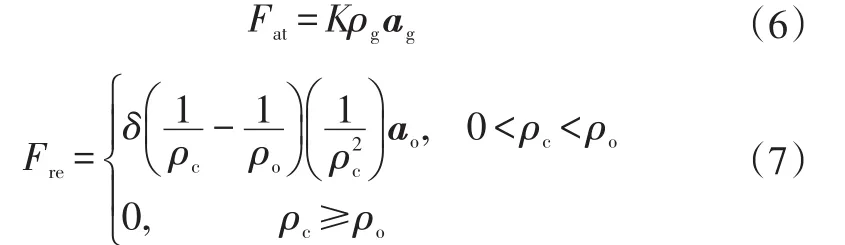
式中，Fat为目标点对被控对象的引力；Fre为障碍物对被控对象的斥力；k为引力增益系数；δ为斥力增益系数；ρc为被控对象与障碍物间的距离；ρg为被控对象与目标点间的距离；ρo为障碍物的作用距离；ao为被控对象指向障碍物的单位向量；ag为被控对象指向目标点的单位向量。

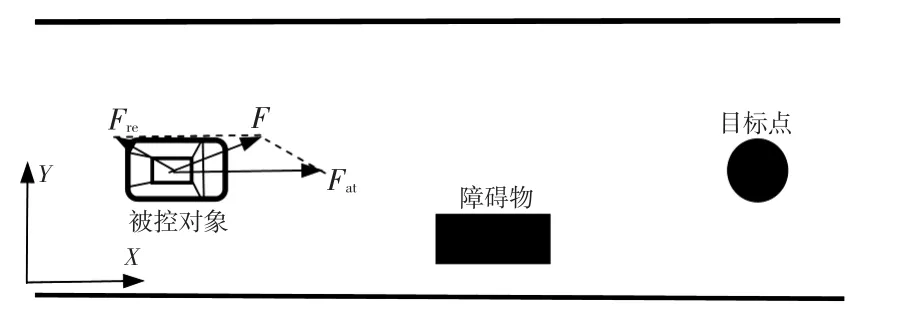
图3 被控对象在人工势场中的受力

3.2 改进的人工势场法

3.2.1 障碍物的作用范围

在传统人工势场法中，障碍物虚拟斥力场的作用范围为圆形区域，作用半径过大或过小得到的规划路径都不符合人类驾驶习惯，也给其他车辆安全行驶带来隐患[7]。

但是在实际超车过程中，由于道路条件所限，以及车辆纵向、横向速度的不同，纵向行驶速度及距离大，侧向速度及距离小，故将障碍物斥力场的范围进行了改进：纵向（X方向）势场作用距离变大，使智能车辆提前修正方向，进行避障；横向（Y方向）势场作用距离变小，使智能车辆迅速驶出避障区域。重新划分后的势场作用域成为椭圆形，如图4所示。在X、Y轴方向上，设定障碍物虚拟势场作用的距离分别为A和B。

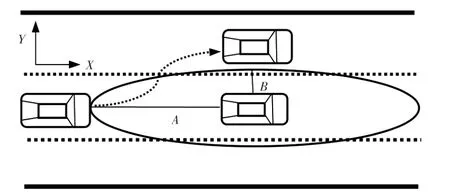
图4 改进人工势场模型

a.椭圆作用域长轴A的确定

由理论分析可知，智能车辆与障碍车辆之间存在最小纵向安全距离，该安全距离与车辆的速度密切相关。但不同障碍物的危险程度不同，如危险品车辆等，碰撞结果造成的危害大、损失多，其安全距离应该增大，故不同类别的障碍物应有不同的避障安全距离。所以，基于不同类别障碍物的危险度，对避障距离A进行修正，即

式中，ζ为障碍物危险级别系数，取值范围为1～1.6。

b.椭圆作用域短轴B的确定

由图4可以看出，在遵守交通规则的前提下，障碍车辆应该在车道内行驶。而根据实际驾驶经验可得，智能车辆在Y轴方向上的避障距离应该等于障碍车辆边缘（靠近超车道一边）到车道线的距离。为使超车行为更加安全，在避撞距离基础上增加安全因子，以车辆行驶在车道中间为例，椭圆作用域短轴B的修正公式为：

式中，§=1.2为安全因子。

3.2.2 斥力函数的改进

传统人工势场斥力函数只考虑车辆与障碍物之间的距离，但在车辆实际行驶中，障碍物的危险程度不仅与两车之间的距离相关，还与障碍车辆的速度、质量、类别等密切相关。一般来说，速度越快、质量越大，则危险越大，且危险品车辆的危害程度要高于普通车辆。基于上述实际情况，本文通过定义斥力系数以及引入斥力调节因子和前车速度来改进传统斥力函数模型。

a. 斥力函数系数δ的确定

实际驾驶中，驾驶员随前车危险程度不同作出不同的驾驶行为。为使智能车辆超车换道行为更人性化，前车危险程度应随其质量和类别变化。在人工势场中，前车危险程度可通过斥力函数系数δ体现在智能车辆上：

式中，M为前车的质量；G为调节基数，防止斥力系数过大；e为自然常数；p为前车类型，其数值可根据危险程度进行设定，并用指数函数进行放大。

b. 斥力调节因子ρg的引入

传统人工势场模型中，控制对象受到的斥力大于引力且方向在一条线上或者受到的引力和斥力不在一条直线上，但是其夹角接近180°时，将陷入局部最小点。为此，在传统斥力场中引入调节因子ρg，使被控对象在局部最小点引力增大、斥力减小，从而解决传统人工势场中被控对象陷入局部最小点的问题[5]。

而文献[12]提出速度势场，在传统斥力函数模型中引入了速度元素。本文基于该斥力函数模型，结合上述分析对传统斥力函数进行改进，如：

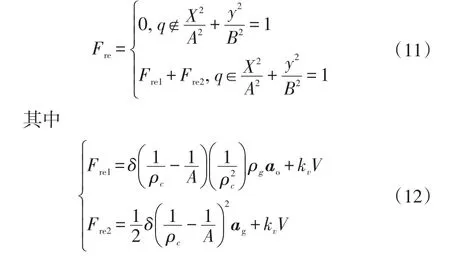
式中，q为被控对象的空间位置；kv为速度势场斥力系数；V为前车的速度。

3.2.3 虚拟局部目标点

文献[8]提出，在满足车辆动力学约束的条件下，超车过程中两车并行的距离为5～8m。基于上述理论，本文提出局部目标点理论，即智能车辆在避障时，系统在车道上生成虚拟局部目标点（见图5），牵引车辆驶向安全区域，并使车辆生成的规划轨迹贴合实际驾驶轨迹。

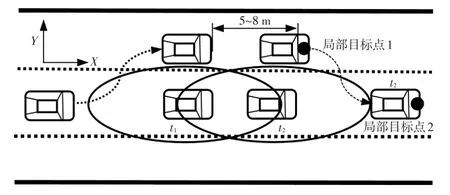
图5 局部目标点的选取

图5中（t1、t2为不同时刻），局部虚拟目标点1的纵向位置与障碍物t1时刻的纵向位置的距离为5～8m，横向位置在无障碍物路道的中央，局部虚拟目标点2的纵向位置相对于障碍物的纵向距离为（A+L），横向位置在障碍物路道的中央，其中，L为车辆长度。

改进的人工势场算法考虑了超车驾驶行为，其在改进的椭圆势场作用域的基础上，引入基于前车运行工况的斥力函数系数、斥力调节因子和建立虚拟局部目标点，使智能车辆在障碍车辆和虚拟目标点合力作用下进行小角度平稳的超车路径规划，更符合实际超车情况。

4 路径跟踪控制仿真

为验证改进人工势场法规划的超车路径是否合理，使用MPC算法[13]跟踪规划路径。在CarSim中建立车辆模型，具体参数如表1所示。利用MATLAB编写路径规划和跟踪控制模块，将在Simulink中建立的MPC控制器与CarSim中的车辆模型以及仿真环境连接起来，构成仿真平台，如图6所示。

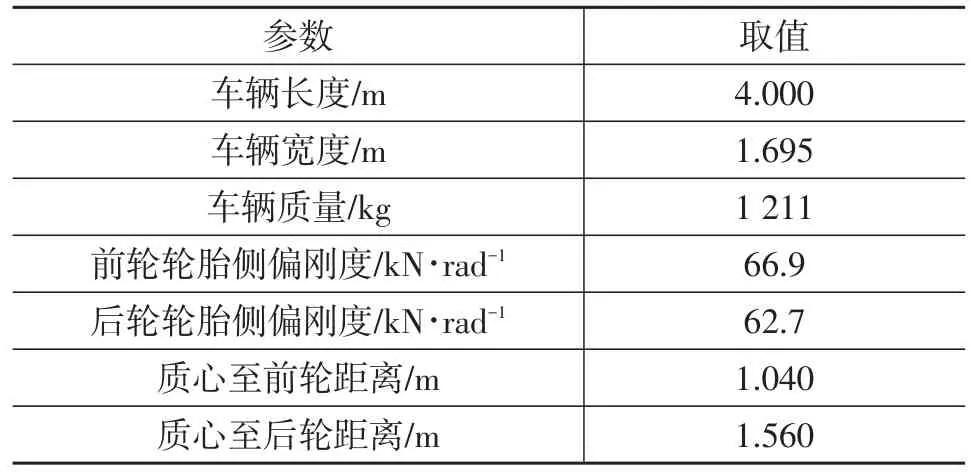
表1 汽车模型参数

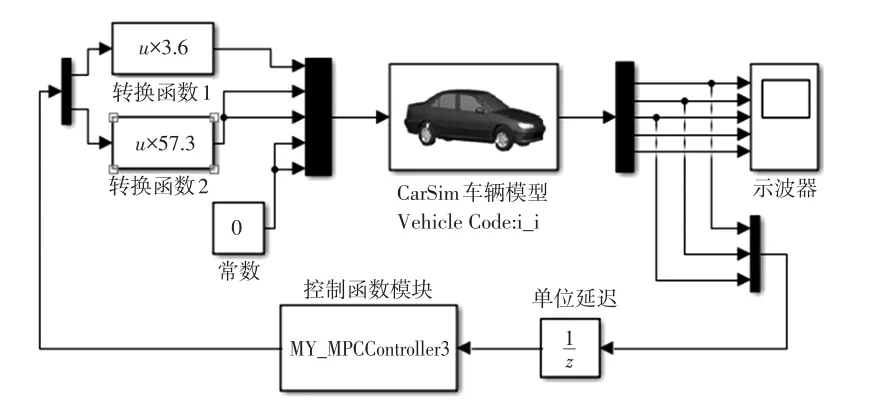
图6 联合仿真平台Simulink框图

本文设定运行路况为双车道路况，智能车辆与障碍车的速度分别为72km/h、50km/h，车道宽度为3.5m，路面附着系数μ=0.75，取ζ=1.5。依据图1所示的超车过程中的不同阶段，对超车轨迹进行跟踪控制。部分动态仿真结果如图7所示。图7a为超车准备阶段，障碍车辆与智能车辆之间的距离较小，此时智能车辆开始侧向偏移，准备换道另一个车道；图7b为超车过渡阶段，智能车辆从行车道换到超车道，从轨迹上可以看出，智能车辆能够平稳地换道，没有撞到障碍车辆；图7c为超车阶段，智能车辆在超车道行驶一段距离，超过障碍车辆；图7d为从超车道换到行车道的过渡阶段，与图7b相似，智能车辆能够平稳换道，没有撞到障碍车辆；图7e为超车结束阶段，智能车辆超过障碍车辆并回到行车道，完成超车行为。

图8所示为智能车辆在超车过程中的参数变化曲线，由图8可以看出，智能车辆在超车过程中车辆角度变化较小，车辆最大转角为1.5°，最大侧向加速度为2.94m/s2＜0.67μg，满足车辆的运动学和动力学约束。

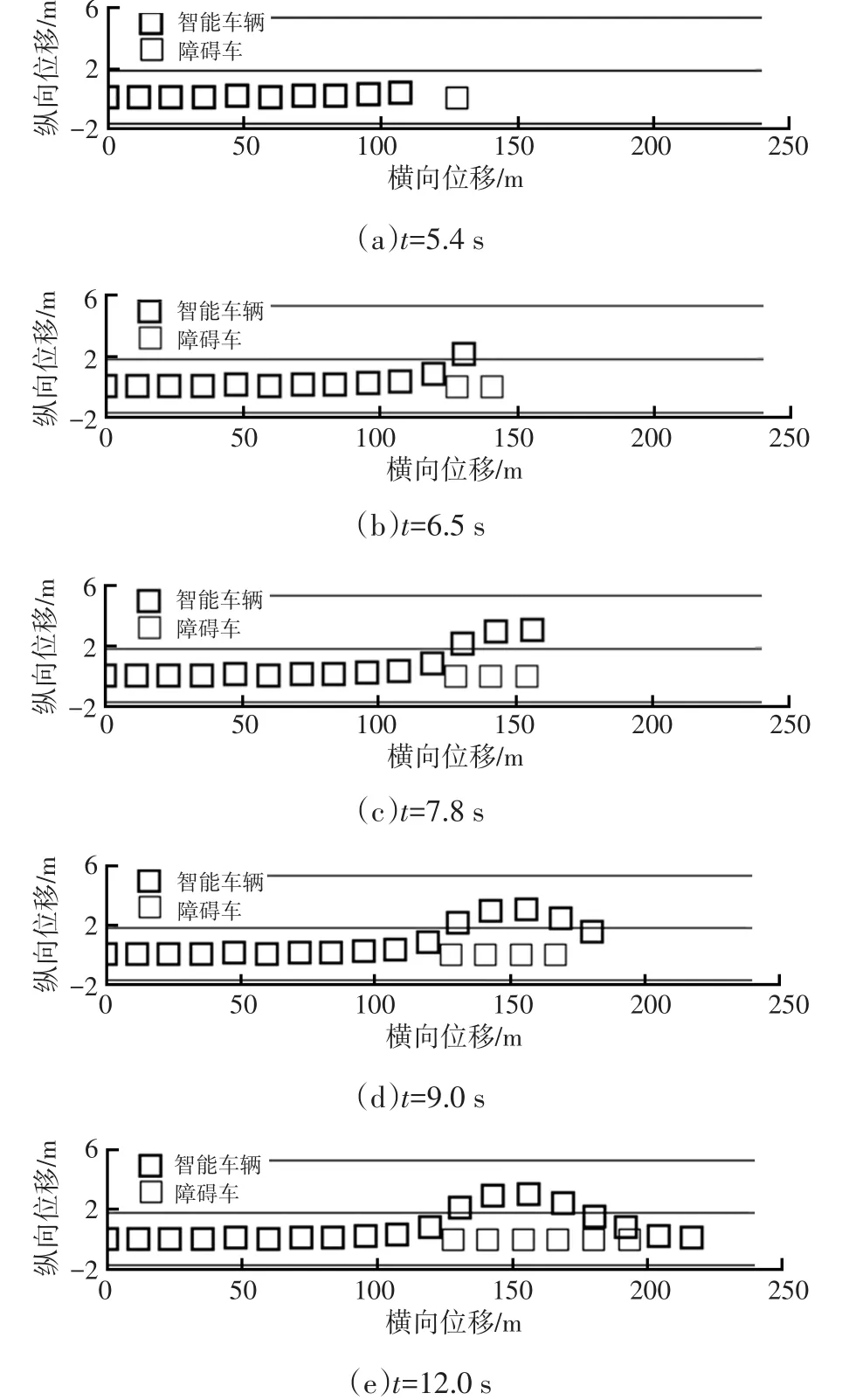
图7 车辆超车过程中的路径规划

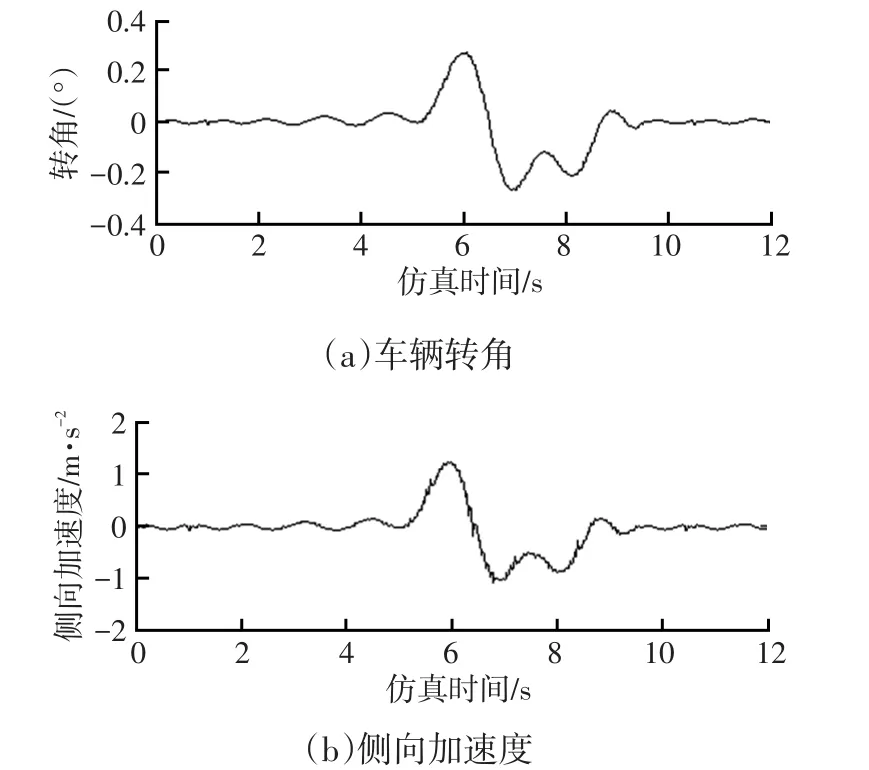
图8 智能车辆超车过程中参数的变化

从以上结果分析可知，改进人工势场法规划的超车路径与驾驶员超车换道结果一致，符合智能车辆超车需求，满足车辆动力学约束与道路约束，达到预期目标。

5 结束语

本文以智能车辆超车换道行为为研究对象，分析驾驶员的超车行为，建立了最小纵向安全距离和超车安全约束模型，并依据上述理论对传统人工势场法进行改进，提出了障碍物斥力场的椭圆形作用域、局部虚拟目标点，改进了斥力函数模型，建立了智能车辆超车路径规划模型。车辆动力学联合仿真验证结果表明，采用改进的人工势场模型使智能车辆安全稳定地超车换道，超车行为更加贴合实际。

在此基础上，后续研究基于驾驶模拟器等方法验证算法的实时性和有效性，进一步研究车辆协同条件下的路径规划与控制问题。

[1]付笛.基于驾驶员与道路环境因素的驾驶行为差错数学分析[D].吉林：吉林大学，2013：16.

[2] Gregory D，Michael J.Computational Principles of Mobile Robotics[M].Cambridge：Cambridge University Press，2000.

[3]罗乾又，张华，解兴哲.改进人工势场法在机器人路径规划中的应用[J].计算机工程与设计，2011，32（4）：1411-1415.

[4]于振中，闫继宏.改进人工势场法的移动机器人路径规划[J].哈尔滨工业大学学报，2011，43（1）：50-55.

[5]修彩靖，陈慧.基于改进人工势场的智能车辆局部路径规划的研究[J].汽车工程，2013，35（9）：53-56.

[6]曹昊天，宋晓琳，黄江.基于弹性绳理论的自主车辆防碰撞的路径规划[J].汽车工程，2014，36（10）：1230-1236.

[7]冀杰，彭和，迟文俊，等.基于危险势能场的车辆避障驾驶行为决策分析[C].2015中国汽车工程学会年会论文集（Volume2），2015：509-512.

[8]谭宝成，崔佳超.改进人工势场法在无人车避障中的应用[J].西安工业大学学报，2014，34（12）：1007-1011.

[9]游峰.智能车辆自动换道与自动超车控制方法的研究[D].吉林：吉林大学，2005：65.

[10]游峰，张荣辉，王海玮，等.基于纵向安全距离的超车安全预警模型[J].华南理工大学学报（自然科学版），2013，41（8）：93-98.

[11]刘存星，魏民祥，顾亮.车辆紧急变道避撞安全距离建模与仿真研究[J].机械设计与制造，2016（2）：17-20.

[12]郭达.智能车避障路径动态规划和车体控制研究[D].西安：长安大学，2015：32.

[13]龚建伟，姜岩，徐威.智能车辆模型预测控制[M].北京：北京理工大学出版社，2014.