CAPM模型在股票市场的实证分析

俞剑楠

【摘要】CAPM模型（Capital Asset Pricing Model）是当代金融市场价格理论的基石，收益率与风险的关系、均衡定价过程是其主要研究内容。伴随着我国股票市场的蓬勃发展，CAPM模型得到了越来越广泛的使用，在进行资产估值、成本预算和资源配置时的重要性日益突出。而股票市场中，银行股分量吃重，因此本文随机选取了8家代表性银行股，对其2015-2016年间的交易数据进行实证分析，采用时间序列检验法，意在测验单因素CAPM模型是否有效。

【关键词】资本资产定价模型；β系数；时间序列检验；有效性；实证分析

一、CAPM模型综述

Markowit首创了资产组合理论，他运用均值一方差行为模型，把理性投资者的投资决策看成是在相同风险前提下追求效用最大化的过程，并说明单个市场主体可以采用多元投资降低风险。以此为理论支柱，William Sharpe、John Lintner、Jack Treynor等人于20世纪六、七十年代提出了CAPM模型。该模型接受了Markowit模型的假设条件，并克服了Markowit理论仅限于刻画单个市场主体投资决策的局限性，说明的是整个市场的全部微观主体投资的情况，对收益率与风险的关系、均衡定价进行了论证，又名标准CAPM模型。该模型的提出使得Markowit资产组合理论得到了更为完整的表述，同时也吸引了一大批经济学家的注意，由此开始了一场金融界的革命。

标准CAPM模型计算公式为：

E（ri）=rf+βim（E（rm）-rf）。

E（ri）——资产i的预期收益率，E（rm）——市场组合的预期回报率；rf——无风险收益率；βim——资产i的β系数，βim=Cov（ri，rm）Var（rm），它衡量的是系统风险，E（rm）-rf——市场风险溢价。

在标准CAPM模型提出之后，又涌现出诸多学者对其进行了扩展，影响比较大的有：Black（1972）发现标准CAPM模型关于无风险利率的假设在现实经济生活中难以实现，继而取消了无风险借贷假设，而将公式中的无风险利率rf以零β的资产收益来代替，创立了所谓的零β的CAPM模型；Michael·Brennan认为税负对资产定价具有不可或缺的影响，将税负的调整引入CAPM模型，使得该模型更符合投资者的心理偏好；迈耶（1972）则提出，并非所有资产都可以根据投资者的意愿迅速交易以使其投资组合实现自身效用最大化，不可交易资产的存在也应考虑到资本资产定价模型当中去，由此确定了更为精确的CAPM模型计算公式。

和西方学者多年来乐此不疲地改进并检验CAPM模型的有效性相似，随着我国股票市场对国民经济的影响力日益提升，国内的专家学者对CAPM模型是否适用于中国股市同样兴趣浓厚。然而，和西方学者普遍接受CAPM的适用性截然相反，2010年以前国内学者的实证研究大部分倾向于否认CAPM模型的有效性，具有代表性的有：施东辉（1996）提出，就上海股市的特征而言，通过多元化投资降低风险收效甚微，其系统风险与预期收益的关系与CAPM模型相悖：杨朝军、刑靖（1998）认为上海股市股票定价没有充分契合CAPM模型，其他因素也会影响股票定价；陈小悦，孙爱军（2000）分析了94-98年共49個月的数据，得出β值不足以解释中国股市的平均收益的结论。这很大程度上是因为中国股市1989年才开始试点，21世纪以前股票市场还很不成熟。不过，近几年我国股市日趋完善，以前的实证研究可能并不符合股市的新变化，因此本文选取了2015年1月到2016年12月的股票历史数据，试图利用最新的趋势再次对CAPM模型进行检验，以期得出不同的结果。

二、数据选取

截至2017年末，中国上市银行股票已达39支，包括25支A股和14支中资H股，银行板块股票占比越来越重，其收益情况对整个股票市场举足轻重，以银行板块为例来对股票市场进行CAPM的实证分析是合理有效的。本文在2017年总市值排名前15的上市银行股票中随机选取了8支股票，分别为工行、建行、农行、招行、交行、中行、民生银行以及中信银行。中国报告大厅的统计数据显示，这8家银行2017年的股票总市值约为74074.72亿元，占整个银行股总市值绝大部分。同时，这八家银行上市时间长，各方面指数比较稳定，且交易数据来源丰富，即使是最晚上市的农业银行，其历史数据也可以追溯到2010年，可以充分提取。并且，这些银行资产规模、经营绩效等各方面因素各有差别，满足了样本多样性的要求。综合而言，上述八家银行比较具有代表性，其数据能够大体上反应整个银行板块股票的情况。

三、模型建立与回归分析

为了进行统计检验，应当将标准CAPM模型（本身为事前模型）转化为事后模型，这样才能将历史数据引入模型进行计算。本模型采用时间序列检验方法，验证的是仅以β值为解释变量的单因素CAPM模型在银行板块的有效性。

进行时间序列检验，学界普遍采用的是BJS方法，即由Fischer·Black、Jenson、Myron·Scholes对CAPM模型进行实证分析时采用的方法。首先将数据分为3个时间区间，2015-01到2015-08，2015-09到2016-04，以及2016-05至2016-12。划定区间后，先后估计单只股票的β值和股票组合的贝塔值，步骤如下。

（一）单只股票B系数的估计

事后CAPM模型的公式不同于标准CAPM模型，可表达为：

rit-rf=αi+βi（rmt-rf）+εi

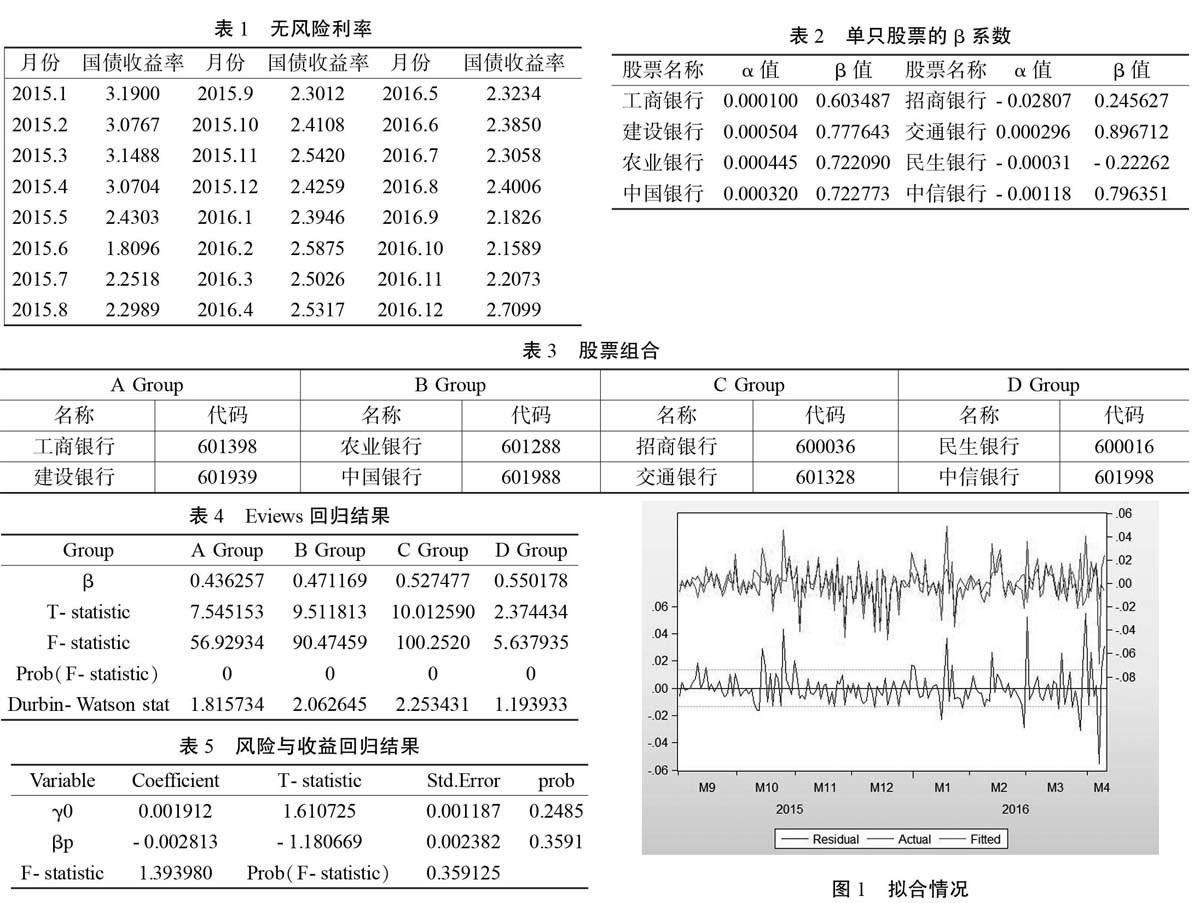
此步骤中的数据均取自2015年1～8月。公式中，rit、rmt是股票i以及市场组合在t日的收益率，且rit=t日收盘价-（t-1）日收盘价（t-1）日收盘价，当日收盘价以及上日收盘价则来源于网易财经的历史交易数据，市场组合的收益率用上证指数在t日的收益率表示；εi是估计残差，且E（εi）=0；采用一年期国债收益率作为无风险利率rf，详见表1（数据由中国货币网获得，收益率数据均为百分数）；αi和βi为模型参数，需要通过该公式计算出来，表2即为Eviews9.0得出的单只股票的β系数。

为简化分析，将三个时间区间内无风险利率看成是不变的常数，其数值由考察时间内一年期国债的平均日收益率求得。根据上表，可得2015至2016年一年期国债的平均收益率为2.3603%，换算成日收益率为0.0065%，即为本模型确定的无风险利率。

（二）组合β系数的估计

由于计算得到的单只股票的p值的差距较小，故不按照p值进行分组，而是按照总市值的高低将八只银行股分为4组，具体分组情况如下：

股票组合β值的计算公式：rpt-rf=αp+βp（rmt-rf）+εp

式中，rpt即股票组合在t日的收益率，按照一般投资者的习惯，分配在投资组合中每种股票的投资额相等，所以rpt等于两支股票日收益率的均值，由2016-09至2016-04的样本数据得到；αp、βp为组合的待估计参数，印同样为估计残差。

选定显著性水平5%、置信水平95%，查表知t的临界值为1.9867，根据表4，所有组合的t>1.9867，即所有组合都通过了t检验。而F检验的P值均为0，说明所有组合的日收益率与β值之间线性关系显著，可继续进行下一步的检验。

（三）风险与收益关系的检验

按照检验公式：rp=γ0+γ1βp+εp再次运用Eviews9.0进行横截面分析，rp即股票组合在2016-05到2016-12的平均日收益率，βp仍为组合β值，γ0、γ1为参数。回归结果及拟合情况如下。

由表5，γ0>0，这与现实情况相符，因为无风险利率是大于0的，但是，γ1<0，表示风险与收益反方向变动，这显然与现实的投资情况截然相反，γ0、γ1的T检验的P值均大于0.05，即在95%的置信水平上T检验并不显著：F检验的P值也远超0.05，没有通过该检验。而且图一表明，该模型的拟合程度很低，拟合系数远远低于1，β值不能完全解释收益率，这证明，仅将p值作为收益率的解释變量的单因素CAPM模型不适用于中国股市。

四、结论分析

本文利用八家上市银行股2015至2016年的历史交易数据，采用BJS方法进行时间序列检验，得出CAPM模型不适用于中国股市的结论。一方面，本文采用的单因素CAPM模型自身具有局限性，它仅用B值来解释投资收益率，而忽略了公司规模和结构、债务偿还能力、风险指标等众多因素；另一方面，本文仅选取了八只股票两年的数据，还要剔除节假日、双休日，样本容量小，误差较大，CAPM模型的适用性低也就不难理解。但最为重要的原因是[6]，中国股市规模小、监管乏力、投资者缺乏科学的投资观念，不满足CAPM模型苛刻的前提条件，与西方国家股市比较而言是一个不成熟、非有效市场。要想使CAPM模型更有效地运用于中国股市，最根本的出路是大力发展股票市场，使之更趋完善。