基于磁致伸缩机理的锚杆无损检测系统设计

2018-03-26孙晨光王明明孙晓云

中国矿业 2018年3期

孙晨光，王明明,孙晓云

(石家庄铁道大学电气与电子工程学院，河北石家庄 050043)

在锚杆的无损检测中，磁致伸缩导波技术因其单端激励、传播距离远、100%横截面检测、非接触性等特点在长距离大范围结构的无损检测和健康监测中显示出良好的应用前景[1-4]。作为电磁超声检测系统中核心部分——磁致伸缩换能器，由于其换能效率低，制约了电磁超声的工程应用。接收端输出电压有时会低到微伏级,而且其对周围环境灵敏度高，信号常常淹没在其他噪声之中，很难分辨。电磁超声检测频率通常在30 k～150 kHz之间，而负载往往是由线圈构成，会带有一定的感抗，使得电路严重不匹配。为了增大传输效率，必须进行阻抗匹配，即线圈和功率放大器之间负载满足共轭关系[5]；而接收端电压信号太微弱导致采集不到有效信息，所以在接收端和信号采集之间加上前置放大电路，可以有效提高信噪比。

武新军等[6]设计了一种非接触式磁致伸缩导波管道无损检测系统，详细阐述了系统的组成部分，实验验证了该系统不仅可以用于管道中，也可用于其他带包覆层细长构件。刘素贞等[7]按照电抗元件网络可准确实现调谐和变阻的特性，结合二进制的组合方式，设计出可以匹配多种频率线圈的电抗网络。该匹配网络能在0.5～5 MHz宽频率范围内有效提高电源的输出效率，提升电磁加载的信噪比及转换效率，为电磁超声的后续研究奠定基础。刘素贞等[8]根据电磁干扰问题设计了消除电磁干扰的硬件电路，构建了具有高速、高共模抑制比、高输入阻抗以及低噪等特点的复合仪表放大器。马洁腾等[9]为了超声导波技术能更好的应用于支护锚杆的检测，采用理论分析和实验室测试的方法对锚固和自由锚杆中的高频纵向导波传播规律进行了研究，从而得到了激发的最佳频率和频率与能量变化的关系。

因此，本文设计了一套基于磁致伸缩机理的锚杆无损检测系统，如图1所示。

图1 系统框图

该系统可有效地检测到信噪比高的导波信号。高斯信号可有效的提高激励线圈的效果；T型阻抗匹配模块的设计既可以升阻又可以降阻，达到了全覆盖；前置放大模块可以放大信号，滤除噪声，提高信噪比。通过仿真和实验的研究，验证了该系统的实用性和有效性。

1 电磁超声激励单元

电磁超声激励单元的主要功能是利用锚杆的磁致伸缩效应，由磁致伸缩传感器在锚杆上激励超声导波[10]。该系统主要由信号发生器、功率放大器、阻抗匹配网络、磁致伸缩激励换能器等组成。

1.1 信号发生器

信号发生器使用泰克公司生产的AFG3052C任意波发生器。磁致伸缩超声导波要求应用窄带脉冲信号进行激励，实验中采用高斯脉冲信号，可以使得能量集中，减少导波模式数，降低信号检测的难度。此外高斯信号的变化比较平稳，有利于功率放大器进行放大,进而提供脉冲大功率激励信号。信号经过功率放大器后加载在激励传感器，就可以在锚杆中激发出磁致伸缩导波脉冲。

1.2 功率放大器

由信号发生器发出的高斯信号无驱动线圈激励导波的能力，须要经过放大器的放大,才能加载到激励传感器上实现超声导波的激励。由于磁致伸缩导波检测使用的频率范围一般为30 k～150 kHz，瞬间功率达到上千瓦，所以一般的功放无法满足要求。本实验使用AETechron 7224功率放大器，它提供了非常低的噪声和快速摆率，并可以安全地驱动电感性负载。该放大器不同于一般的50 Ω输出阻抗放大器，该放大器分为高电压、中模式、高电流三个档位；每个档位对应不同的输出阻抗。在使用该功率放大器前应对其进行阻抗匹配以保护功率放大器和得到最优放大效果。

1.3 阻抗匹配模块

阻抗匹配模块主要有τ型、反τ型、T型和π型四大类[11-12]。对于所需负载小于本身负载的电路，要选用升阻型(τ型)，其原理图如图2所示。而对于所需负载小于本身负载的电路，要选用降阻型(反τ型)阻抗匹配网络，其原理图如图3所示。X1、X2、X3为阻抗匹配的电抗元件，Req为负载的电阻值，Xeq为负载的电抗值。若负载为感性负载，匹配元件即为电容。

不论是τ型电路还是反τ型电路，从阻值较大的一侧思考(不论是负载阻抗还是输出阻抗)，需要先并联电纳以降低该阻抗实部模值，再串联电抗。即在不进一步改变实部大小的前提下，消除先前并联的电纳对虚部的影响，实现匹配。

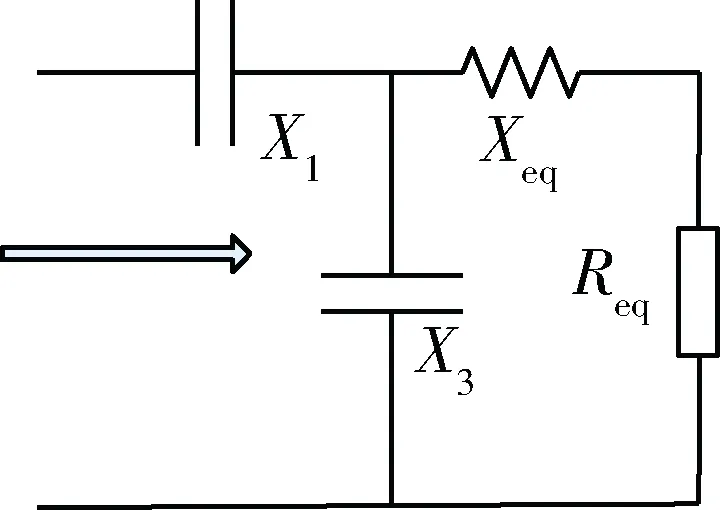
图2 τ型网络

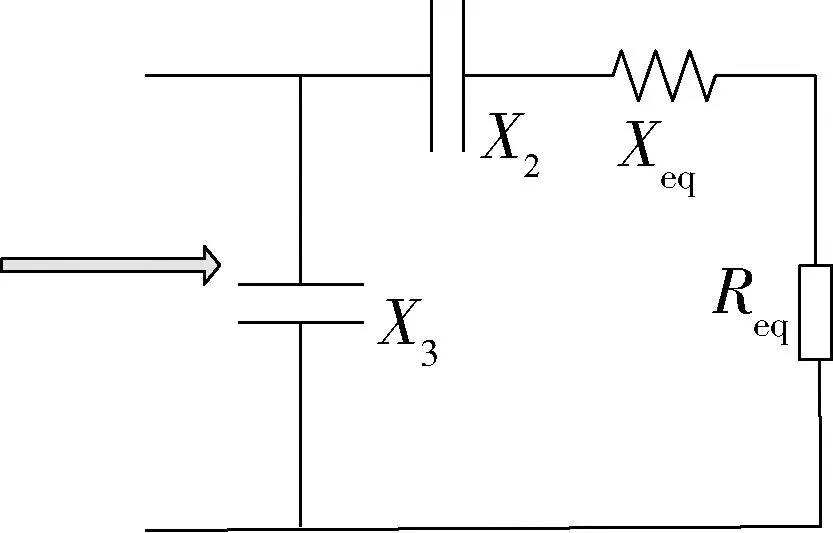
图3 反τ型网络

所使用的功率放大器有高电压、中模式、高电流三个档位，不同的档位对应不同的输出阻抗。当为高电压模式时，功率放大器所需要匹配的电阻较大；当为高电流模式时，其所需要匹配的电阻较小；当为中模式时，其所需要匹配的电阻介于两者之间。为了满足使用要求，既能达到升阻效果又能达到降阻效果，本文设计一种T型阻抗匹配网络，如图4所示。当S1断开、S2闭合时，其为升阻网络电路；当S1闭合、S2断开时，其为降阻网络电路。

使用Smih圆图法[13]来简化计算，以升阻型网络为例进行计算。特性阻抗为20 Ω，负载的电阻和电感分别为0.9 Ω、0.13 mH，频率为40 kHz。画图轨迹如图5所示。标记1为负载值，经过串联电容到标记2，电容大小为139.6 nF，再并联电容到标记3，并联电容大小为913 nF，标记3即为特性阻抗20 Ω。

1.4 磁致伸缩换能器

对于锚杆的检测要采用纵向导波模态[14]。纵向模态导波是以存在径向和轴向位移分量为特征的轴对称波，其条件是周向位移为零，且轴向和径向位移与角度无关，此时横截面上径向位移的平均值为零，轴向位移的平均值不为零。为了在锚杆中激励出纵向导波，这就要求交变磁场和偏置磁场的磁场方向均平行于锚杆的轴线方向,且均匀分布于锚杆周向。激励换能器激励线圈采用直径为0.51 mm漆包线缠绕而成，偏置磁场使用钕铁硼永磁铁。

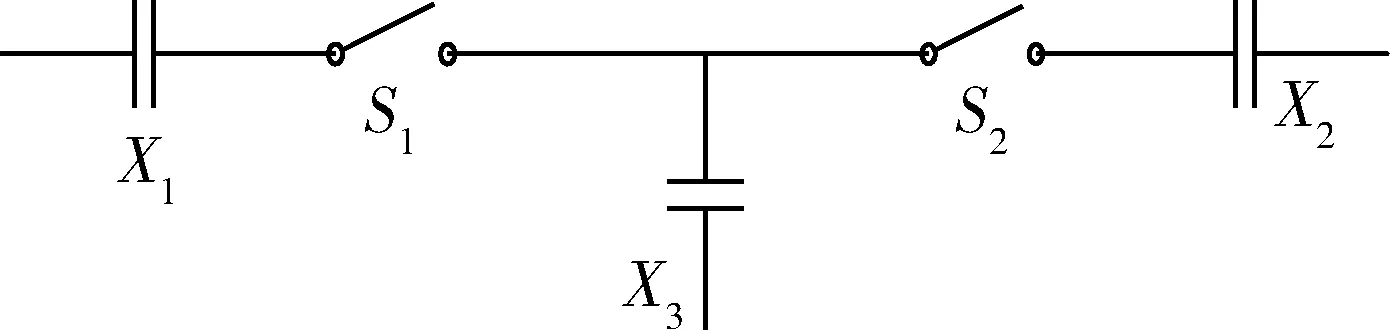
图4 T型网络

2 电磁超声接收单元

导波接收单元的主要功能是利用铁磁体的磁致

伸缩逆效应,由磁致伸缩传感器接收锚杆中激励超声导波，该系统主要由磁致伸缩接收传感器、前置放大模块、信号采集等组成。磁致伸缩接收换能器结构同激励端，线圈使用直径0.21 mm的漆包线缠绕而成。

2.1 前置放大模块

前置放大电路原理图如图6所示。

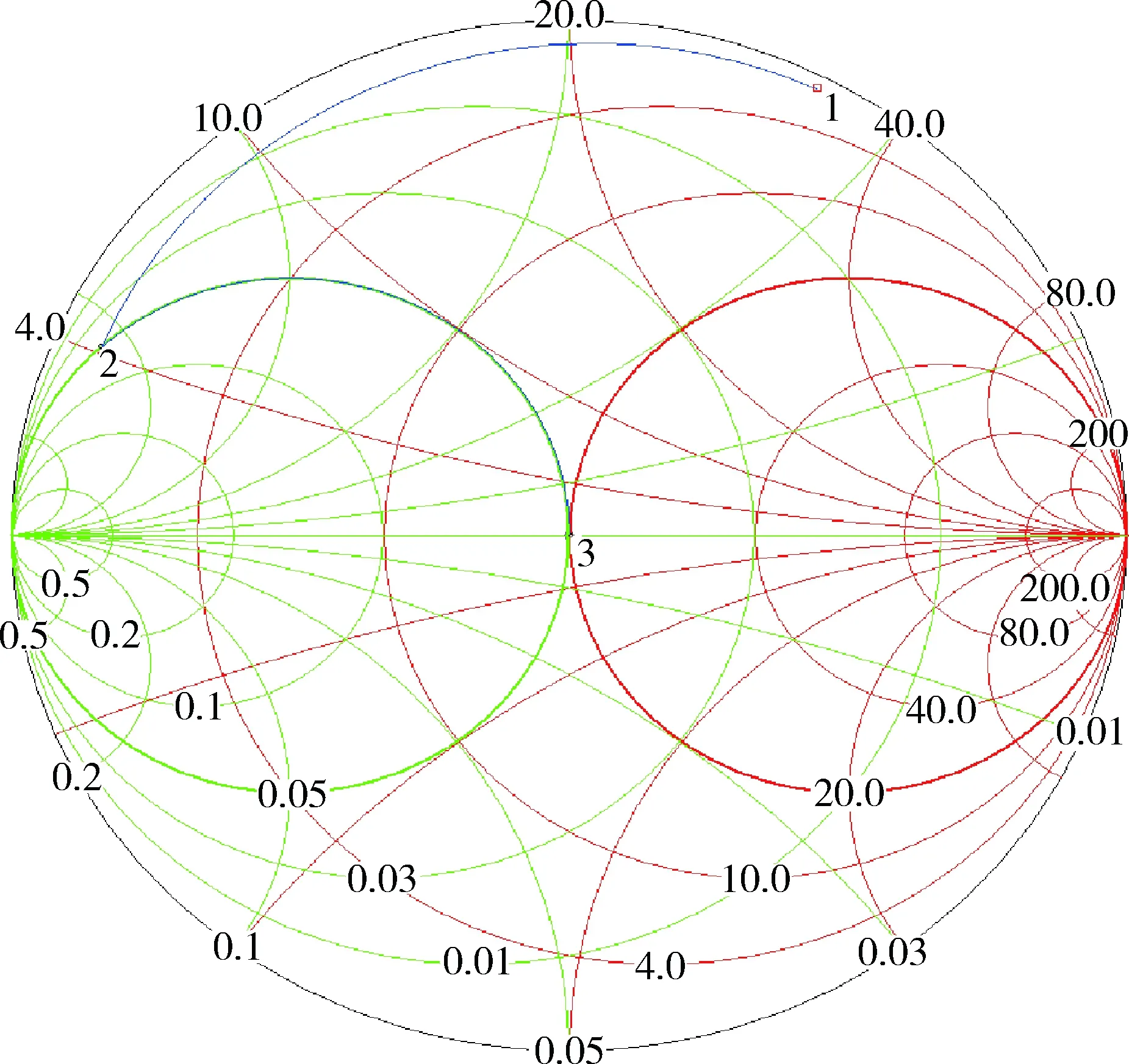
图5 Smith圆图轨迹

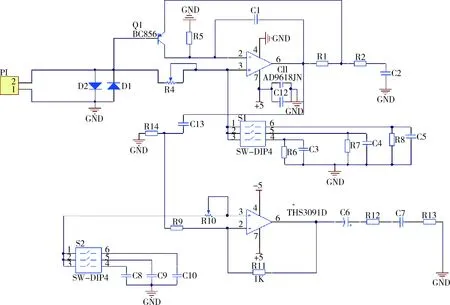
图6 前置放大电路

功率放大器在放大信号时产生强烈的电磁干扰，因此在放大电路的输入端，加入了限幅电路。该电路由两个一对二极管 D1、D2 反向并联组成。当检测信号经过限幅电路时不会有明显的衰减，而发射电路的高压电磁干扰会被二极管直接短接，有效地保证了接收电路的安全性。

第一级放大使用三极管作为输入器件，以集成运放作为第二级放大，输出加以高通滤波，同时配以电阻和电容实现外围补充，使得通频带内增益的性稳定和输入阻抗都较高，而输出阻抗较低；使用三极管结构替代一般的集成运放，使得电路结构简单，成本低，稳定性方面与双运放放大电路相当；采用滤波电阻R6和滤波电容C3等并联接入第二级级联的放大器的正向端与地之间，进一步除去干扰信号，使滤波效果更理想；电阻R5与C1串联接电阻R1的连接关系，可提高级联放大器的相位裕度、展宽频带，从而可实现宽带宽的稳定放大增益。在集成运放芯片电源处加C11、C12起到去耦的作用。

为了能够针对30 k～150 kHz范围内的不同频率信号产生满足要求的移相角度，本文通过拨码开关来选择不同电容值的电容，以实现在不同频率段内的相位偏移，再通过调节R10即可实现所需要的移相角度。然而，在这里电容的选择显得至关重要，因为它不仅影响着电路的移相角度，还影响着电路能否保持输出信号幅值保持基本不变。其上一级电路相当于一个信号源，而信号源会有内阻，即上一级电路的输出阻抗。R10和C8等串联形成的阻抗即为移相电路的输入阻抗，当不需要移相时R10=0，因此1/2πfC8不能太小。

2.2 信号采集

由于经过放大后的信号也是毫伏级的，还是很微弱，所以要使用灵敏度高的采集卡。本实验所使用的是东华测试的DH5923N系列的采集系统。该采集卡灵敏度高，既可以采集加速度信号也可以采集电压信号。而且其上位机软件界面友好，自带简单滤波效果，方便快捷。

3 检测系统仿真

3.1 阻抗匹配模块仿真

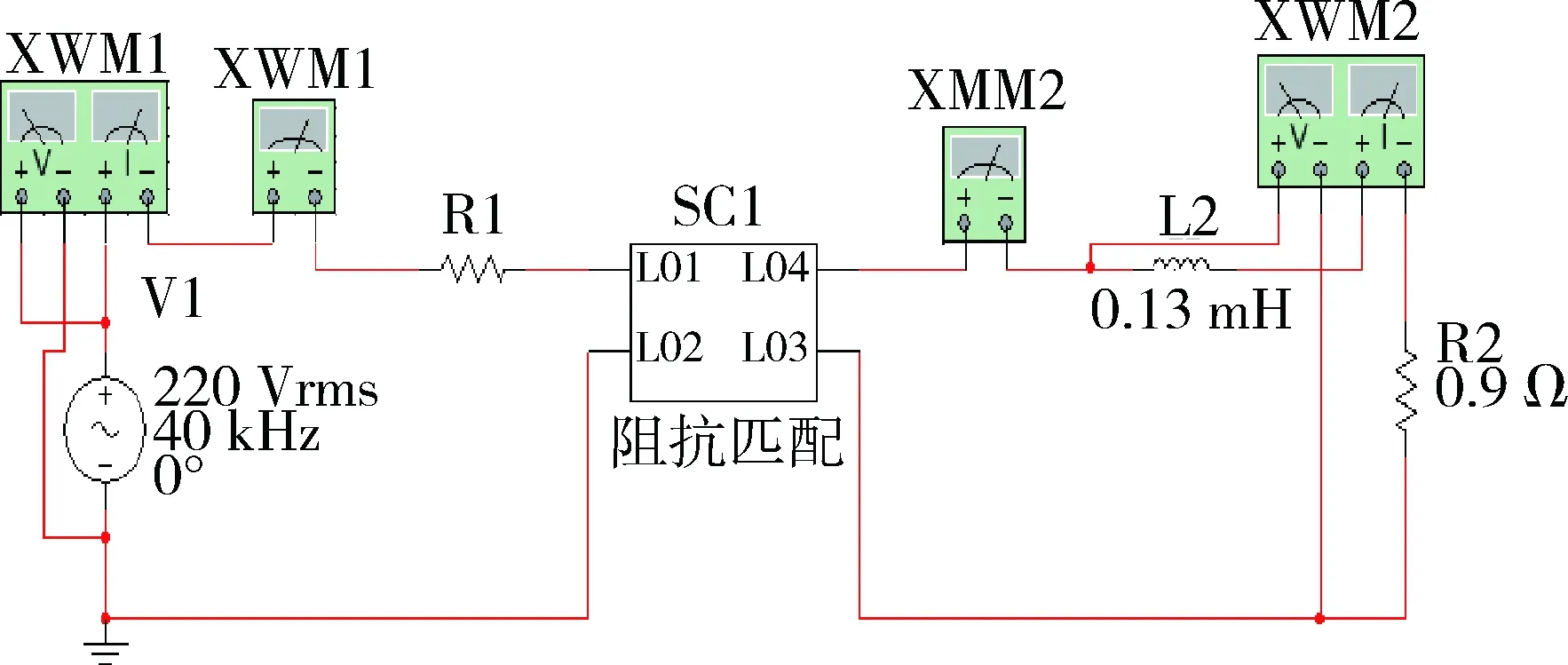
图7 阻抗匹配仿真电路

使用Multisim14进行仿真验证。采用激励为40 kHz交流信号，线圈的电阻和电感分别为0.9 Ω和0.13 mH。分别以升阻20 Ω和降阻0.3 Ω为例进行仿真，仿真如图7所示。图7中Leq和Req分别是激励线圈的电阻和电感值，R1为其等效阻抗值，SC1为其阻抗匹配网络电路。为了方便观察，仿真中加入了探针，可以实时观测其电压和电流值。使用交流分析仿真，观测升阻型和降阻型等效阻抗的变化值，其结果如表1和表2所示。表1为等效阻抗为20 Ω时的仿真结果，表2为等效阻抗为0.3 Ω时的仿真结果。

当R1为20 Ω时，作为升阻型阻抗匹配可以有功率传输效率最大处，其仿真结果如表3所示。有匹配时电流明显增大，功率传输效率也由4.31%增大到43.02%。

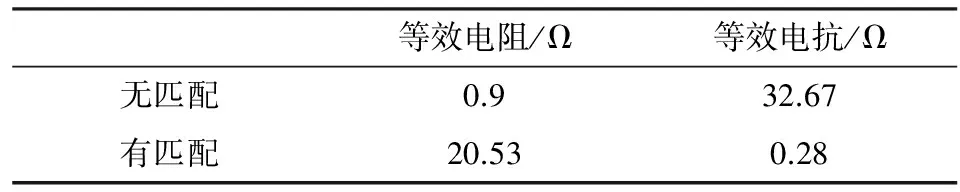
表1 有、无阻抗匹配下的电阻和电抗值对比(20 Ω)

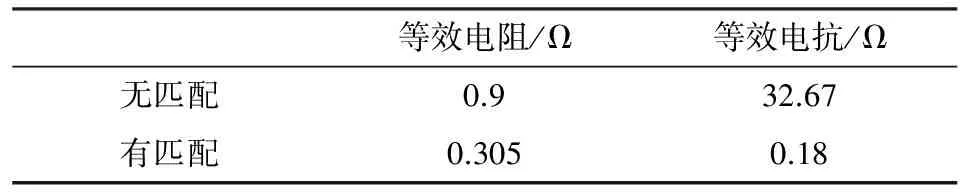
表2 有、无阻抗匹配下的电阻和电抗值(0.3 Ω)

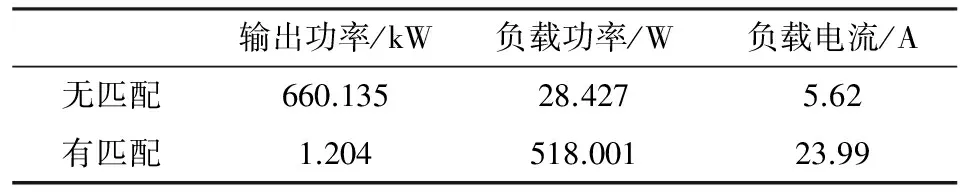
表3 有、无阻抗匹配电流和功率的对比

3.2 前置放大模块仿真

仿真选择频率为40 kHz，峰值为20 mV的信号源。放大电路采用的是BC856晶体管和AD9618集成芯片，可有效降低噪声，放大微弱信号。仿真电路图与原理图一样。图8是频率在40 kHz时改变增益选择所得到放大倍数的仿真图。图9是频率在40 kHz时改变增益选择所得到相位角的仿真图。图10为不改变相位角时的波形图。图11为改变相位角时的波形图。

图8(a)放大倍数：G=1 542/19.676≈78.37；图8(b)放大倍数：G=1 393/19.933≈69.88；图8(c)放大倍数：G=2 155/19.749≈109.12。

仿真结果可以得出：前置放大电路对信号实现的正向放大，相频特性较好；能够实现毫伏信号的放大，放大性能稳定。由计算结果可知在40 kHz时候，放大倍数分别约为78倍、70倍、109倍，且信号也基本上没有失真现象，满足设计要求。

在实际应用中，往往因器件老化或电路中电容或者电感等不准确等因素的影响，造成相位偏移。为此，本文在放大电路后增加了等幅移相调节模块，调整滑动变阻器，使相位值达到最大，结果见图9。

由图9(a)可以得出，在40 kHz输入信号的情况下，S2开关4关闭5、6打开，调节光标到x=40 kHz,可以得到移相角度为0.047°，即该通道不改变相位；同理可得其他两种情况，S2开关5关闭4、6打开、S2开关6关闭4、5，相位角为-94.948°和-178.268°。通过改变滑动变阻器使得相位在0.047～-94.948°和0.046～-178.268°之间改变，从而避免使得相位偏移所导致的计算误差。

图10和图11可以看出通过调节电位器阻值使相位发生了改变，但幅值几乎不变，且不失真。所以一个幅值不变，相位可变的前置放大电路设计满足要求。

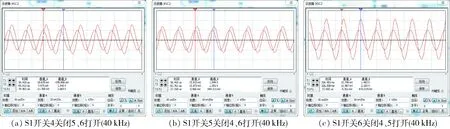
图8 改变增益选择所得到放大倍数

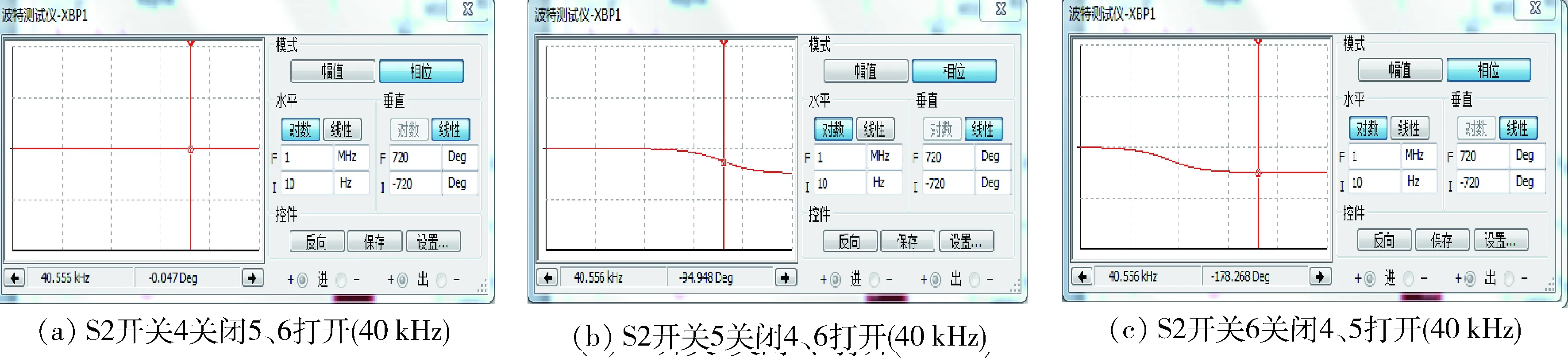
图9 改变增益选择开关所得到相位角

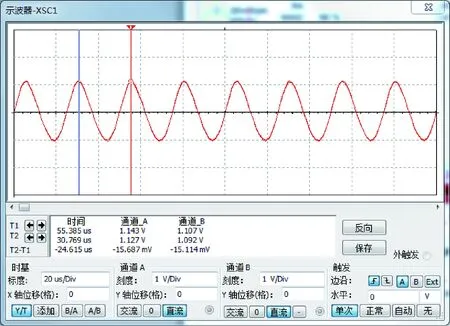
图10 不改变相位角

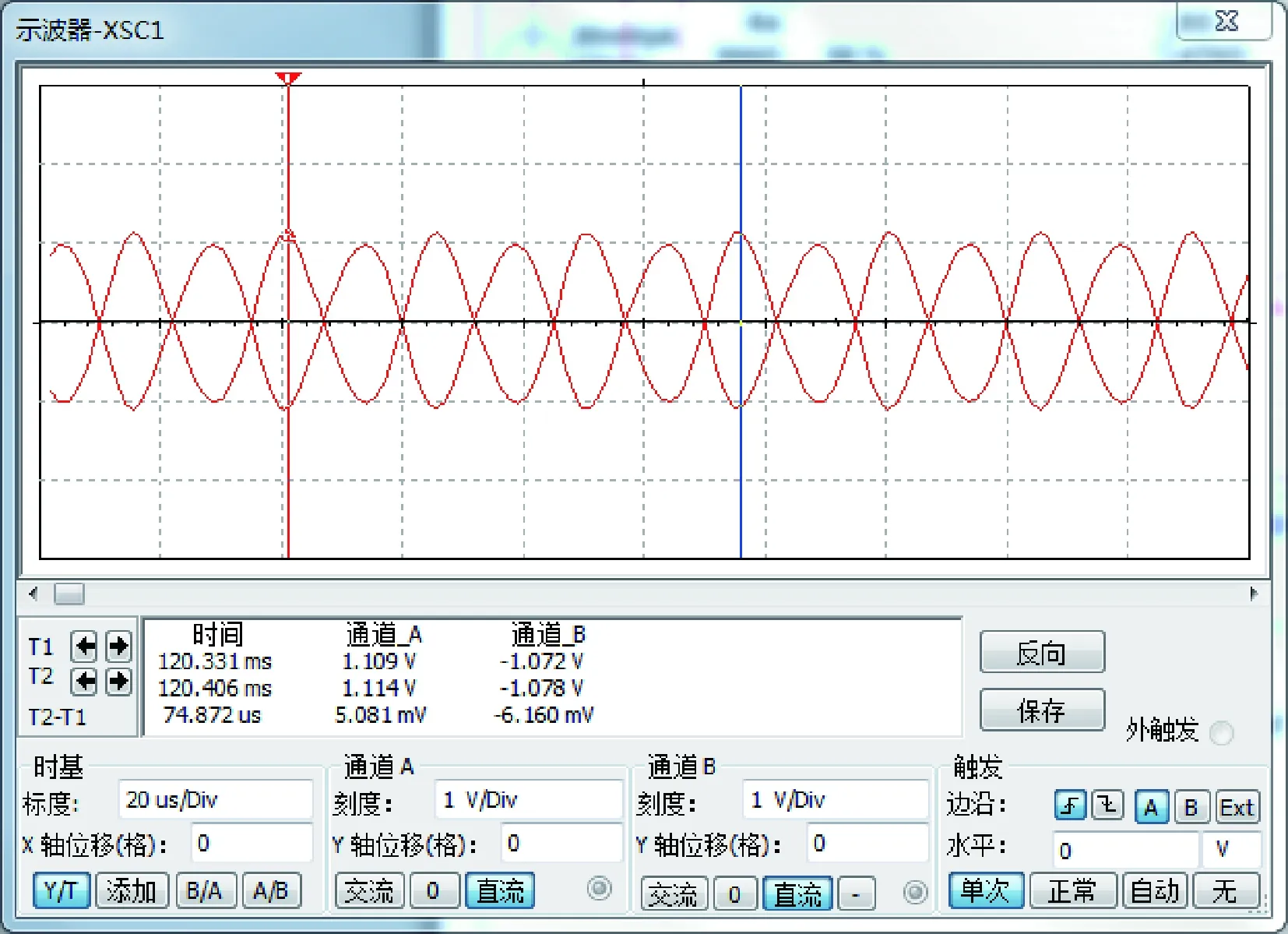
图11 改变相位角

4 检测系统实验

检测系统主要由信号发生器、功率放大器、阻抗匹配电路、前置放大电路、磁致伸缩换能器、采集卡和3 m长的裸锚杆构成。激励换能器距离右端面60 cm，接收换能器距离右端面125 cm；在距离左端面60 cm处做了一个深度为5 mm的裂缝缺陷，即与接收端相距115 cm。使用信号发生器发射一个频率为40 kHz脉冲信号，通过功率放大器放大信号，经阻抗匹配后激励磁致伸缩传感器，使裸锚杆中产生特定频率的超声导波。超声导波经过接收端将震动信号转换为电压信号传给前置放大电路，由仪器内部的采集模块对数据进行接收和模数转换，并在计算机内部编写的示波软件中进行数据的显示、分析与存储。图12为采集到的信号。

实验结果表明：阻抗匹配网络的加入使激励系统的换能效率得到了大幅度提高，信号明显，易于观察，为接下来的信号处理提供了帮助，也对功率放大器起到了一定的保护作用；而前置放大电路的加入则对信号进行了初步处理，使有用信号得以放大，回波信号峰值大约达到了50 mV，滤除掉噪声，使得波形更加直观。

由图12及上位机软件可看出,第一次通过信号对应时间约33.10295 s，缺陷信号峰值与第一次通过信号相差0.00047 s。由于采样频率为100 kHz,每两个点时间间隔为0.00001 s，读数误差在允许范围内。超声导波在被检测频率段的锚杆中的传播速度为4 900～5 100 m/s[15],选择5 000 m/s进计算，在误差允许范围内。则接收端与缺陷之间的距离为5 000×0.00047/2=117.5 cm，与实际缺陷位置仅相差2.5 cm；第一次左端面回波信号时间为33.1037 s，与第二次左端面回波信号时间差为0.00122 s，相差的是两个锚杆长，锚杆长为0.00122×5 000/2=305 cm，与实际长度相差5 cm。其结果见表4。

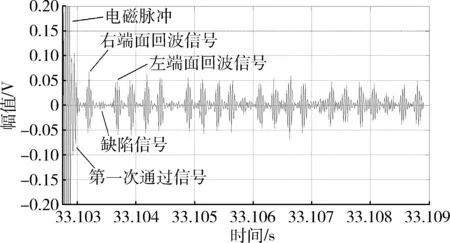
图12 采集信号

表4 测试结果及误差分析

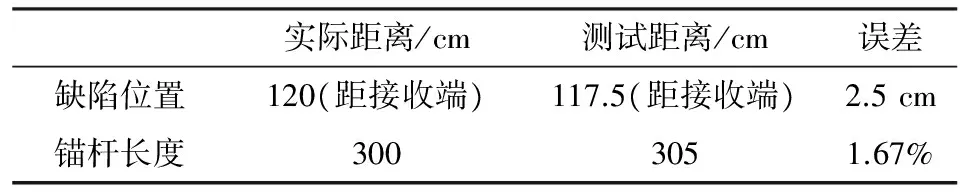
实际距离/cm测试距离/cm误差缺陷位置120(距接收端)117．5(距接收端)2．5cm锚杆长度3003051．67%

从表4可以看出，缺陷位置只差2.5 cm，而且锚杆的长度误差仅为1.67%。误差在允许范围内，可以说该系统设计是合理的。

5 结论

本文设计了一种基于磁致伸缩机理锚杆无损检测系统，作为系统中最重要的两个部分：阻抗匹配模块和前置放大模块，通过电路的测试与仿真，表明测试结果与设计指标一致。而在锚杆无损检测系统中的应用，可以较为准确的测量出锚杆的长度及缺陷位置，为锚杆的安全使用奠定了基础，同时也表明了电路性能良好,但是该电路输出信号还存在一定的不足,噪声信号还是比较大。后续任务是对滤波电路再进行处理,进一步提高信噪比，能更好的满足检测要求。

1) 高斯信号变化平稳，有利于功率放大器进行放大提供脉冲大功率激励信号。

2) Smith圆图法对于阻抗匹配网络的设计，达到了简化计算的目的；而且T型阻抗匹配网络的设计既可以升阻也可以降阻，达到了全覆盖。

3) 通过仿真和实验验证：增加阻抗匹配电路可以使得传输效率接近50%，电流增大，信号幅值提高；前置放大电路可以放大有用信号，滤除噪声，提高了信噪比。

4) 通过观察波形，考虑到速度、读数等误差的分析，计算出缺陷位置仅差2.5 cm，锚杆长度误差为1.67%，检测系统设计合理。

[1] Dixon S,Burrows S E,Dutton B,et al.Detection of cracks in metal sheets using pulsed laser generated ultrasound and EMAT detection[J].Ultrasonics,2011,51(1):7-16.

[2] 吴斌,曹海洋,刘秀成,等.干耦合式磁致伸缩导波管道检测系统[J].无损检测,2016,38(9):9-13.

[3] Jian X,Dixon S,Grattan K,et al.A model for pulsed Rayleigh wave and optimal EMAT design[J].Sensors and Actuators A:Physical,2006,128(2):296-304.

[4] 刘素贞,王晨光,张闯,等.电磁超声扫描装置及其控制系统的设计[J].电工技术学报,2015,30(10):20-25.

[5] 郝宽胜,黄松岭,赵伟,等.电磁超声换能器新型线圈阻抗及匹配电容的计算[J].高技术通讯,2010,20(8):845-849.

[6] 武新军,徐江,沈功田.非接触式磁致伸缩导波管道无损检测系统的研制[J].无损检测,2010,32(3):166-170.

[7] 刘素贞,张严伟,张闯,等.电磁超声激励系统阻抗匹配网络的设计[J].电工技术学报,2016,31(16):1-6.

[8] 刘素贞,李丽滨,蔡智超,等.电磁超声检测系统中消除电磁干扰电路的设计[J].电工技术学报,2016,31(1):80-84.

[9] 马洁腾,张昌锁,潘立业,等.高频纵向导波在锚杆检测中的应用[J].煤矿安全,2013(10):34-37.

[10] 刘洋.磁致伸缩导波锚杆无损检测实验研究[D].杭州：浙江大学,2010.

[11] 李引凡,陈政,邱洪云.天线调谐器T形阻抗匹配网络参数估算[J].现代电子技术,2013,36(8):7-9.

[12] 卢文成,丘小辉,毛行奎.磁谐振无线电能传输系统的最大效率分析[J].电气技术,2015(4):14-17,21.

[13] 何思远,贺菁菁,黄冉冉,等.Smith圆图理解和使用的几个关键问题[J].电气电子教学学报,2016,38(5):58-60.