2018年高考数学（理科二卷）导数解答题解题研究及教学建议

□海南省海口市第一中学 陈文彩

2018年导数解答题考查了学生对导数知识的掌握程度和导数在研究函数性质中的作用，在秉承以往能力立意的基础上，关注到素养立意。

理科第21题：已知函数f（x）=ex-ax2.（Ⅰ）若a=1，证明：当x≥0时，f（x）≥1；（Ⅱ）若f（x）在（0，+∞）上只有一个零点，求a.

一、整体评价这个题的设计

第（Ⅰ）问设计合理，难度适中。考查学生对导数、极值、单调性的深层理解，以及二阶求导的能力，还考查学生变通的能力，即使没有考虑到二次求导，还可以用换元法转化成新函数再求导。除此之外，还考查学生解题的规范性，特别是求极值时要先判断单调性。

第（Ⅱ）问设计灵活，难度偏易。考查学生的综合分析能力，此题有分离参数和分类讨论两大解法，在时间紧迫的考场上需要学生能综合分析题意，选择较简单的解题方法。选择分离参数法，计算简单，但需考虑端点取值；选择分类讨论，计算繁杂，难以讨论清楚。

二、学生答得较好的地方

一是部分学生不会用二次求导，但也懂得先用换元法转化成新函数再求导；二是第（Ⅱ）问会做的学生中，大部分应该是用分离参数法做出来的，仅有少数会用分类讨论的方法做出。

三、学生答得不足的地方

一是应该存在部分学生不会解方程ex=2，甚至不会第一步求导，提交白卷。二是不明白求导的意义，盲目求导，甚至盲目求二阶导、三阶导，求完不知接下来做什么。三是个别学生求导后会直接判断最小值，不考虑单调性。四是个别学生会把极值点代入原函数而不是一阶导函数。五是第（Ⅱ）问分离参数时，有部分学生会读题不准，分离的是导函数的参数而不是原函数的参数。六是用分离参数法的学生会有很多没有考虑端点的取值而导致不能拿到满分。

四、给高三备考的建议

本题难度较以往降低，题型比较常规，方法比较大众，没有出现偏题、怪题和太刁难的题目，对导数的考查主要是极值、最值和零点问题，应用的方法主要是二阶求导和分离参数法，在设计时比较注重细节，注重解题的规范性，还注重题目的综合分析能力，解题方法的选择。

建议后面高三备考时，在导数上抓基础、抓常规题型、抓解题的规范性、抓易扣分的细节，注重关注一元函数的极值、最值、单调性、切线问题，关注含参数的恒成立问题和零点的存在性问题，以及已知恒成立、零点而反求参数的问题。

在讲每一种题型时，提供多种解法、多方面多维度地分析求解题目，提升学生综合分析题目的能力，提升学生选择解题方法的能力，注重思维的宽、广、细，在保证基础、常规、细节、规范格式的基础上再进行适度的拓展。

很多学生不能真正理解导数与单调性、极值最值的关系，所以在一阶求导后不能想到二阶求导，今后的教学可以给学生分析清楚求导的目的和意义，让学生在吃透概念的基础上进行教学会事半功倍。

五、给高二新课的授课建议

新课教学时，要先熟记基本的求导公式，分析清楚导数的本质，导数与单调性、极值最值、图像之间的关系，函数与方程的关系，以及他们之间的相互转化的思想。

注重解题的规范性，教师教学时也要严格按照规范，不能随便出现考试不能用的记号，比如箭头，该写的步骤不能随便省略，学生会模仿，习惯了就改不掉。平时作业、测试要严抓解题格式，该严格扣分就严格扣分，一定要让学生在初始学习时就养成良好的解题习惯。

注重细节，易扣分的细节要告诉学生，并且多在考试中考查这些细节，让学生养成注重细节的习惯。

加强常规题型的练习，降低难度，提升思维的宽度，研究多方法解决问题的能力，研究各种解法之间的关系，提升综合分析能力，在考试中能选择较便捷的解题方法。

六、常见解答方法

第（Ⅰ）问

解法1：当a=1时，f（x）=ex-x2.

f'（x）=ex-2x.

则f''（x）=ex-2，令ex-2=0得x=1n 2.

当x＞1n 2时，f''（x）＞0，则f'（x）在（1n 2，+∞）上是增函数；

当0≤x＜1n 2时，f''（x）＜0，则f'（x）在［0，1n 2）上是减函数；

所以f'（x）min=f'（1n 2）=e1n2-21n2=2（1-1n2）＞0.

所以f（x）在［0，+∞）上是增函数.

所以f（x）≥f（0）=1.

解法2：当a=1时，f（x）=ex-x2，f'（x）=ex-2x.

令g（x）=ex-2x，x∈［0，+∞），则g'（x）=ex-2.

令ex-2=0得x=1n2.

当x＞1n2，g'（x）＞0，则g（x）在（1n2，+∞）上是增函数；

当0≤x＜1n2时，g'（x）＜0，则g（x）在［0，1n 2）上是减函数；

所以g（x）min=g（1n2）=e1n2-21n2=2（1-1n2）＞0.

即f'（x）＞0，所以f（x）在［0，+∞）上是增函数；

所以f'（x）≥f（0）=1.

解法3：当a=1时，f（x）=ex-x2.

f（x）≥1等价于（x2+1）e-x-1≤0.

设函数g（x）=（x2+1）e-x-1，则g'（x）=-（x2-2x+1）e-x=-（x-1）2e-x.

当x≠1，g'（x）＜0，所以g（x）在（0，+∞）上单调递减

而g（0）=0，故当x≥0时，g（x）≤0，即f（x）≥1.

解法4：当a=1时，f（x）=ex-x2，f'（x）=ex-2x.

令fy=ex，y'=ex.

函数y=ex的图像在点（x0，ex0）处的切线方程为y-ex0=（x-x0）.

当该切线经过原点（0，0）时，0-ex0=ex0（0-x0），得x0=1，即函数y=ex的图像经过原点的切线方程为y=ex.

由于e＞2，所以x≥0时，ex0=ex≥2x.

所以f（'x）=ex-2x≥0在x≥0时恒成立.

所以 f（x）在［0，+∞）上是增函数.

所以 f（x）≥f（0）=1.

第（Ⅱ）问

解法1：f（x）在（0，+∞）上只有一个零点，

即x＞0时方程 f（x）=ex-ax2=0有且仅有一解

即x＞0时方程 f（x）=ex-ax2=0等价于a=e2x

x

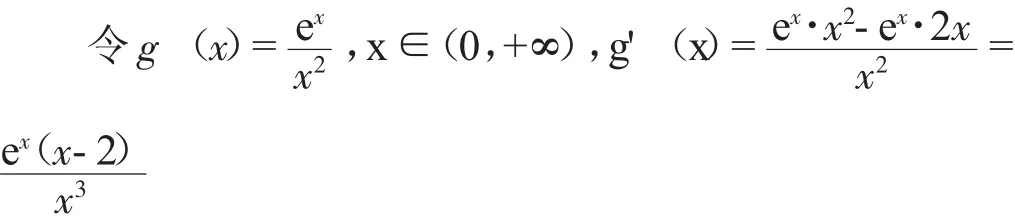
令g（'x）=0得x=2

令g（'x）＞0得x＞2，则g（x）在（2，+∞）上是增函数.

令g（'x）＜0得x＜2，则g（x）在（0，2）上是减函数.

因为x→0时，g（x）→+∞；x→+∞时，g（x）→+∞.

所以g（x）min=g（2）=

所以当a=e42时（fx）在（0，+∞）只有一个零点.

解法2：

设函数h（x）=1-ax2e-x.

f（x）在（0，+∞）上只有一个零点当且仅当h（x）在（0，+∞）上只有一个零点.

（i）当a≤0时，h（x）＞0，h（x）没有零点；

（ii）当a＞0时，h'（x）=ax（x-2）e-x.

当x∈（0，2）时，h'（x）＜0；当x∈（2，+∞）时，h'（x）＞0.

所以h（x）在（0，2）上单调递减，在（2，+∞）上单调递增.

①若h（2）＞0e，即a＜，h（x）在（0，+∞）上没有零

点；

零点；

由（1）知，当x＞0时，ex＞x2，所以h（4a）=1-=1-

故h（x）在（2，4a）上有一个零点，因此h（x）在（0，+∞）上有两个零点.

综上，（fx）在（0，+∞）上只有一个零点时，a=

解法3：

当 （fx）在（0，+∞）上只有一个零点时，

即x＞0时方程 （fx）=ex-ax2=0且仅有一解，

亦x＞0时即方程ex=ax2有且仅有一解.

令g（x）=ex，x∈（0，+∞），h（x）=ax2，x∈（0，+∞），

则方程ex=ax2有且仅有一解时，

函数g（x）=ex，x∈（0，+∞），h（x）=ax2，x∈（0，+∞）的图像有且仅有一个公共点，

设该点横坐标为x0，

则函数g（x）=ex，x∈（0，+∞），h（x）=ax2，x∈（0，+∞）的图像在x=x0处有公切线

g（'x）=ex，h（'x）=2ax，则，解得x0=2，a=。