一种新颖的体积排阻色谱加宽效应的去除方法I理论测试

张 鹏

(1.长江师范学院 电子信息工程学院,重庆 408003；2.华中科技大学 同济医学院，湖北 武汉 430030)

为了简单起见，本文只针对线性聚合物进行讨论。另外，值得讨论的是，带加宽效应可以由色谱柱、内部检测器或者两者共同引起。目前的方法仅使用单一探测器获得的SEC数据。如果实验使用多探测器，那么该方法需要分别应用于每个探测器。

2 理论计算方法

带加宽效应的影响通常采用Tung卷积方程[15]来描述：

(1)

其中，V是洗脱体积，S(V)是SEC探测信号(实际测量的SEC分布曲线)，w(logM)是准确的SEC分布曲线(没有带加宽的曲线)，M是分子量。G(logM,V)是加宽函数。我们选择国际上广泛被认可的EGH函数作为加宽函数：

(2)

这里σ和τ是加宽函数的两个参数，C是归一化常数。

图1展示了本文提出的方法思路：

1、将一组不同样品的SEC观测信号(也就是测量得到的SEC分布曲线，S(V))进行退卷积处理(方程(1)的逆运算)得到相应的一组退卷积后的SEC分布曲线，w(logM)。在第一次退卷积过程中，任意赋予加宽函数中的两个参数σ和τ各一个初始值。

2、分别对每一条退卷积后的SEC分布曲线，w(logM)， 依据方程(3)：

(3)

(4)

的值尽可能为零。这里，n是样品的数目。此时σ和τ值就是我们最终所需要的结果。这样，就可以运用这一组σ和τ值退卷积任意一条由该SEC仪器得到的分布曲线(对于不同的仪器需要重新计算获得一组σ和τ值)得到准确的未加宽的分布曲线。

(6)

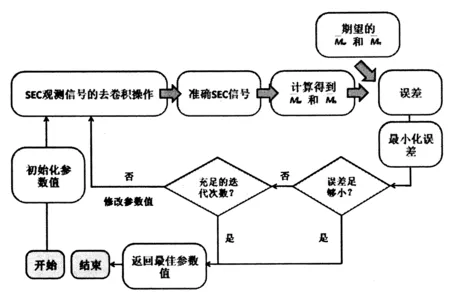
图1 方法流程图Fig.1 Illustrating the new method

3 结果与讨论

在本文提出的方法中，正确的退卷积运算对最终的结果起着非常重要的作用。因为虽然理论上退卷积的曲线必然会和原来的实验重合，但是准确的退卷积的过程依赖正确的运算方法。不恰当的运算操作可能会导致错误的结果，所以在本文中有必要采用可靠的退卷积方法。图2展示了用传统Ishige退卷积算法和本文加入了最大熵算法(方程(6))的修正退卷积算法运算的结果比较。显然，图1(a)中，如果实验SEC分布曲线用Ishige算法退卷积，结果会有很大的涨落，而且退卷积运算的迭代次数越多，涨落越大。这里迭代次数是1000次。这是因为实验的分布曲线中即使非常小的一点涨落会在迭代的过程中放大。图2(b)展示了加入了最大熵算法的修正方法的退卷积结果，可以看出涨落消失了。

虽然，修正的退卷积方法可以消除涨落，但是为了进一步证明修正的退卷积方法是正确的。我们进行了测试。给定一系列σ 和 τ值利用方程(1)分别卷积一条实验SEC分布曲线。再用同样的σ 和 τ值进行退卷积运算。如果退卷积的曲线可以和原来的实验曲线重合，那么说明修正的退卷积方法是正确的。图3展示了测试的结果。

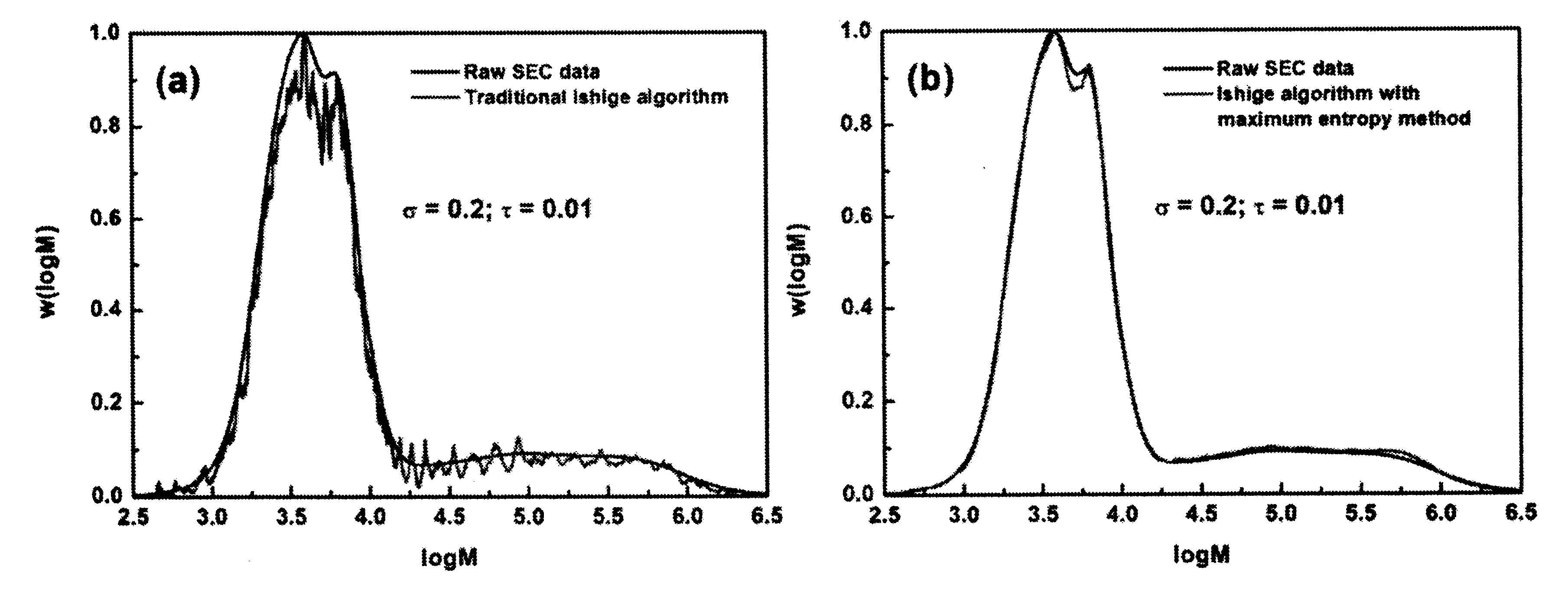
图2 传统Ishige退卷积算法和本文加入了最大熵算法的修正退卷积算法的运算结果比较。(a)实验SEC数据用传统Ishige退卷积算法结果；(b)实验SEC数据用本文加入了最大熵算法的退卷积算法(方程(6))的结果。其中σ=0.2以及τ=0.01。退卷积运算的迭代次数是1000次。实验数据来自文献[17]。所有数据均已归一化。Fig.2 A comparison on results from traditional Ishige algorithm and that with maximum entropy method added upon for deconvolution procedure. (a) raw SEC data deconvoluted by traditional Ishige algorithm; (b) raw SEC data deconvoluted by Ishige algorithm with maximum entropy method. σ=0.2 and τ=0.01. Time of iteration in deconvolution is 1000 times. Raw SEC data was taken from [17]. All the data has been normalized.

图3 (a)从上至下分别使用σ=0.2，τ=0.01；σ=0.4，τ=0.02以及σ=0.6，τ=0.03带入方程(1)卷积的结果；(b)(a)图的相应退卷积结果。实验数据来自文献[17]。所有数据均已归一化。Fig.3 (a) Convoluted results respectively with given σ=0.2，τ=0.01；σ=0.4，τ=0.02 and σ=0.6，τ=0.03 (from top to bottom); (b) the corresponding deconvoluted results for (a) from top to bottom. Raw SEC data was taken from [17]. All the data has been normalized.

图3(a)展示了给定的三组σ 和 τ值带入方程(1)卷积一条原始实验曲线的结果。图3(b)展示了相应的退卷积结果与原始实验曲线的比较，与图(a)相比，显然它们重合的很好。证明修正的退卷积算法是正确的。图4 (a)和(b)分别展示了在σ 和 τ空间中一条Metropolis抽样轨迹以及方程(5)中χ随计算迭代次数变化的曲线。本例中，σactual和τactual值分别是0.45和-0.02。σguess和τguess的值分别是0.70和0.00。显然，轨迹成功地从从初始值(start)搜寻到目标值(end)。相应的，在迭代计算的过程中，χ也汇聚于稳定值。

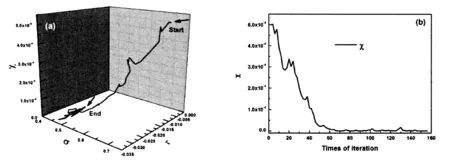
图4 (a)在σ 和 τ空间中一条Metropolis抽样轨迹；(b)方程(5)中χ随计算迭代次数变化的曲线。Fig.4 (a) The Metropolis sampling trajectory of χ in space of σ and τ; (b) Tendency of value of χ with iteration time.

对于本文的方法，做了7组测试，如表1所示。为了定量的描述σconverged和τconverged的值与σactual和τactual的值的接近程度。本文给出了相对误差δσ和 δτ。它们的表达式是

(7)

从表1中可以看出，σconverged和τconverged的值与σactual和τactual的值差别很小。但是为了讨论这个差别是否会造成重大影响，本文用σconverged和τconverged以及σactual和τactual分别带入方程(1)卷积同一系列原始SEC分布曲线(不同样品的SEC分布曲线)，比较卷积后的两条曲线，若重合，则表示误差造成的影响可以忽略。为了使结果有说服力，在此，本文选择了表1中相对误差最大的第一组σconverged和τconverged与σactual和τactual进行计算。

表1 本文方法的7组测试，δσ 和 δτ 是相对误差Table 1 Seven groups of test about our method, δσ and δτ are the relative error

图5展示了比较的结果。曲线重合的很好，误差不会造成影响。

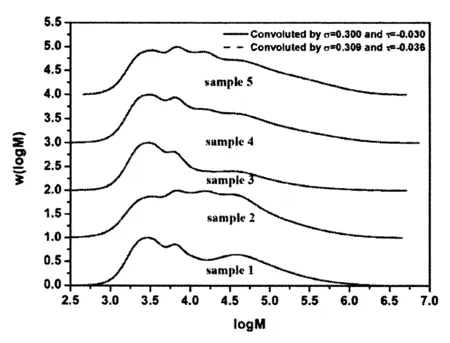
图5 (a)不同样品的实验SEC分布曲线分别用σconverged和τconverged以及σactual和τactual卷积的结果比较。为了清楚展示，每条曲线的纵坐标向上平移。Fig.5 A comparison on the convoluted results of raw SEC data using σconverged and τconvergedbetween using σactual and τactual. All the data has been normalized. In order to distinguish different samples, curves were shifted on the vertical axis. In here, the parameters in table 1 shows the largest relative error through seven groups of test were chosen, that are, σactualis 0.300, τactual is -0.030, σconverged is 0.309 and τconverged is -0.036.

4 结论

针对由于带加宽效应的存在导致SEC分布曲线加宽、扭曲等现象，本文提出了一种有效的去除方法，并对此方法做出了详尽的理论测试。测试的结果显示从非SEC方法(没有带加宽效应)获得的和可以被用来寻找SEC的加宽函数的参数。从而可以很好的通过退卷积运算真实的SEC分布曲线。

[1] STRIEGEL A M, YAU W W, KIRKLAND J J, et al. Modern size-exclusion liquid chromatography-practice of gel permeation and gel filtration chromatography[M]. John Wiley & Sons, Hoboken, 2009.

[2] SCHNÖLL-BITAI I, MADER C. How much does band broadening adulterate results deduced from chromatograms measured by size-exclusion chromatography really[J]. J Chromatog A， 2006(1137)：198-206.

[3] CLAY P A, GILBERT R G. Molecular weight distributions in free-radical polymerizations. Model development and implications for data interpretation[J]. Macromolecules，1995(28)：552-569.

[4] VAN BERKEL K Y, RUSSELL G T, GILBERT R G. Molecular weight distributions and chain-stopping events in the free-radical polymerization of methyl methacrylate[J]. Macromolecules，2005(38)：3214-3224.

[5] GRUENDLING T, GUILHAUS M, BARNER-KOWOLLIK C. Fast and accurate determination of absolute individual molecular weight distributions from mixtures of polymers via size exclusion chromatography-electrospray ionization mass spectrometry[J]. Macromolecules, 2009(42):6366-6374.

[6] GRUENDLING T, VOLL D, GUILHAUS M, et al. A perfect couple: PLP/SEC/ESI-MS for the accurate determination of propagation rate coefficients in free radical polymerization[J]. Macromolecular Chemistry and Physics, 2010(211):80-90.

[7] SATO H, ICHIEDA N, TAO H, et al. Data processing method for the determination of accurate molecular weight distribution of polymers by SEC/MALDI-MS[J]. Analytical Sciences， 2004(20)：1289-1294.

[8] GRITTI F, GUIOCHON G. The van deemter equation: assumptions, limits, and adjustment to modern high performance liquid chromatography[J]. Journal of Chromatography A， 2013(1302)：1-13.

[9] MILLER C T, GRAY W G. On the algebraic and differential forms of Darcy's equation[J]. J Porous Media， 2011(14)：33-50.

[10] BAUMGARTEN J L, BUSNEL J P, MEIRA G R. Band broadening in size exclusion chromatography of polymers. State of the art and some novel solutions[J]. J Liquid Chromatography & Related Technologies， 2002(25)：1967-2001.

[11] SACTO P. A novel automatic dilution system for online particle size analysis[J]. ACS Symp Ser, 1998(693):23-29.

[12] YOSSEN M M. Determination of the band broadening function in size exclusion chromatography with light-scattering detection[J]. Journal of Liquid Chromatography & Related Technologies, 2012，35(1):79-94.

[13] GRAY J G, DUDAS S, CZUB S. A study on the analytical sensitivity of 6 BSE tests used by the canadian BSE reference laboratory[J]. PLoS One, 2011(6):e17633.

[14] GRUSHKA E. Characterisation of exponentially-modified gaussian peaks in chromatography[J]. Anal Chem, 1972(44):1733-1738.

[15] TUNG L H. Method of calculating molecular-weight-distribution functions from gel-permeation chromatograms[J]. J App Polym Sci, 1966(10):375-385.

[16] KIRKPATRICK S, GELATT C D, VECCHI M P. Optimization by simulated annealing[J]. Science,1983(220):671-680.

[17] LI C, LIU G Q, LIU Q Q, et al. Haracterization of the time evolution of starch structure from rice callus[J] Arbohydrate Polymers, 2015(127):116-123.