耦合体系拓扑空间的局部损坏与子空间的重构

张季谦, 宣守智, 谢朔俏, 张健生, 徐 飞, 黄守芳

(安徽师范大学 物理与电子信息学院，安徽 芜湖 241000)

引 言

意大利学者Dorigo等人在观察蚂蚁觅食习性时发现，它们总能找到巢穴与食物源之间的最短路径[1]。蚂蚁这种群体协作功能是通过一种遗留在其来往路径上被称为信息素(Pheromone)的挥发性化学物质来通信和协调的。因此，1992年Dorigo在他的博士论文中提出一种算法：蚁群算法，其灵感来源于蚂蚁在寻找食物过程中发现最短路径的行为。1998年Dorigo在比利时主持召开了第一届蚁群算法研讨会，很快掀起了蚁群算法的研究热潮，随后，Dorigo等人发表第一篇关于蚁群算法专刊，总结了蚁群算法已取得的成果及其应用。

蚁群算法最早成功地解决了旅行商(Traveling Salesm Problem)问题[2]，随后许多科研工作者尝试用蚁群算法去解决各种组合优化问题。在发展了离散蚁群优化算法之后，人们又发展了用于连续变量优化体系的蚁群优化算法。其一种思路是Socha用连续概率密度函数代替离散概率分布, 提出用多个正态分布函数混合的蚁群优化算法[3]。另一种思路则是利用混沌来描述蚁群搜寻食物行为, 建立用于连续变量的混沌蚁群优化算法[4]。为提高对连续空间求解的有效性，我们对蚁群算法进行了改进，将其用于混沌系统部分序列的参数辨识并证实可用于保密通信[5, 6]。

人们发现，单只蚂蚁的行为具有混沌特征，但蚁群的整体则表现出较强的协作和自组织特性[7]。蚁群算法的思想正是基于真实蚂蚁寻找食物的过程，用信息素去调控蚂蚁在寻找食物的路径选择。蚁群在搜寻食物的过程中要遵循一定移动规则，即在行进过程中蚂蚁会通过信息素来沟通和共享信息，对比所选路径的优劣，最后整个蚁群会找到一条最佳路径，该路径的选择过程就对应于我们求解组合优化问题最优解的过程[8,9]。

因而,有个问题值得人们去探索：对于神经网络系统，若神经元之间的耦合联系出现了故障或断路，生物体自身能否找到替代的信息通路呢？很显然，这与蚁群寻找食物过程中, 道路突然被新的障碍物所封堵，蚁群能否构建出新的路径空间来完成食物的寻找过程相类似。为回答这样的问题,首先，我们构造一个在蚁穴和食物源之间具有多条搜寻路径的拓扑空间结构模型。接着，假设蚁群在搜索食物的过程中，该空间拓扑结构发生局部改变或出现缺损。然后，采用蚁群优化算法进行模拟计算，让蚁群调整搜索策略，寻找新的替代路径，构建出让耦合体系重新达到最优状态时所对应的拓扑结构，计算出相应的连接通道。最后，利用路径上信息素浓度的变化特点来判断是否找到了新的路径。

1 蚁群算法及路径空间的结构模型

1.1 蚁群优化算法

(1)

其中，α和β分别表示信息素和启发式因子的相对重要程度，(1)式中的ηij为预见度即信息素量，allowedk={1,2,…，n}表示蚂蚁下一步允许选择的城市。由于蚂蚁在寻找食物时，是通过分泌信息素来进行通信联系和调整各自路线的，因此，蚂蚁在沿途所留下的信息素浓度的高低反映了其所找路径的好坏优劣。这样，在蚁群空间中所有路径都会存在一定浓度信息素，其浓度越高，说明这条道路被蚂蚁选中的概率越大，也就越接近蚁群所要寻找的最优路径。当所有蚂蚁完成一次周游后，各路径上的信息素根据下式更新。

τij(t+n)=ρ×τij(t)+Δτij

(2)

(3)

其中ρ(0<ρ<1)表示信息残留系数，用1-ρ表示信息素的挥发系数。按照上述算法规则，蚂蚁可以搜寻出找到食物的最佳路径。蚂蚁k所走过的路径便是TSP问题的一个可行解。

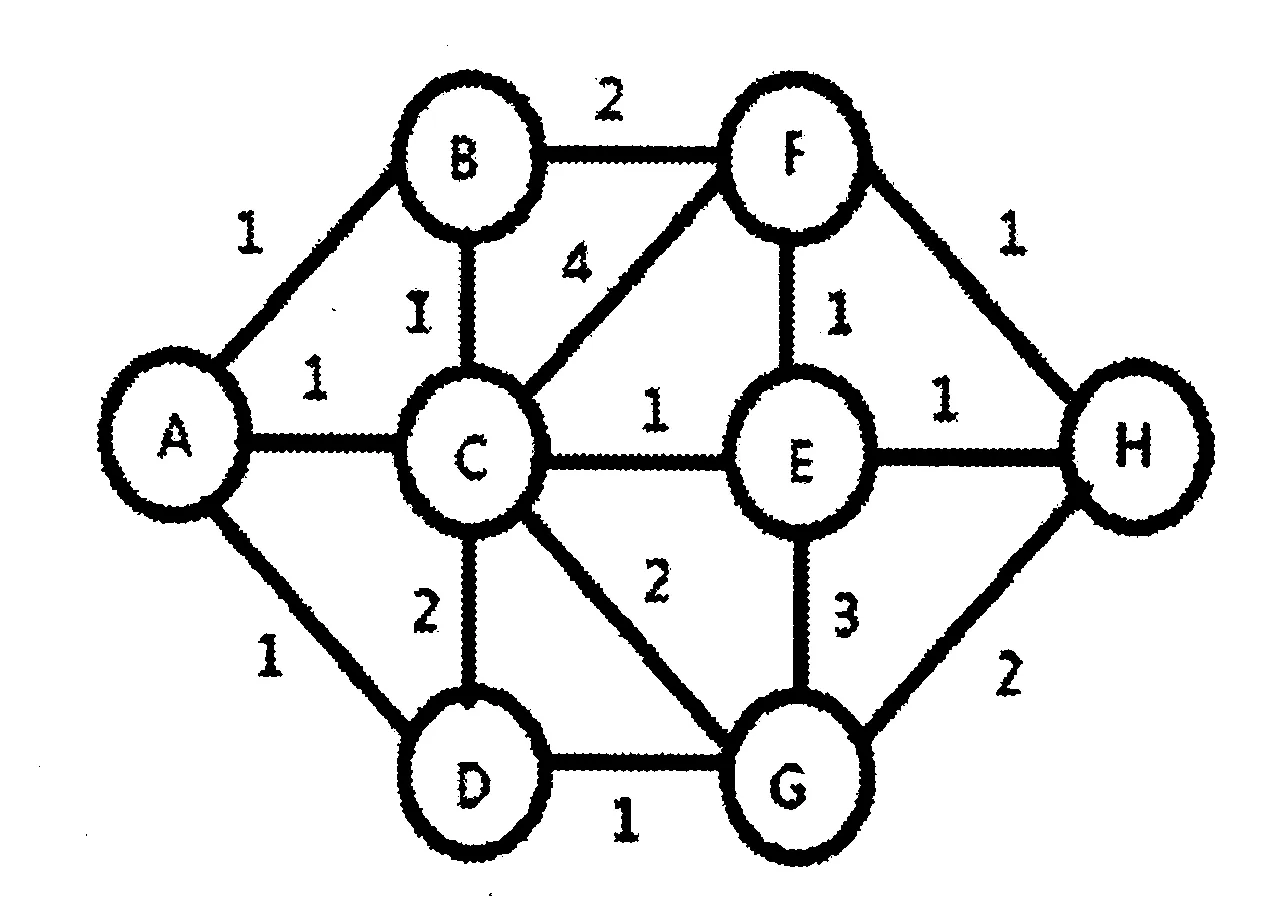
图1 蚁群搜寻食物的路径空间模型示意图。A为蚁穴，H为食物源, 图中数字代表节点之间路径长度。Fig1. Diagram of the path space model of ant colony searching for food. A is a nest, and H is the food source, the numbers represent the path length between nodes.

1.2 蚁群搜寻路径空间模型

路径空间是指蚂蚁在寻找食物过程中，经历各个节点(城市)所有路径构成的空间，这对应于我们解决最优化问题的参数空间。本文设计一个蚁群搜索食物的路径结构模型，如图1所示，其中A点是蚁穴，H点是食物源。蚁群在A点和H点之间运动，B、C、D、E、F、G是中间的节点。开始时，蚂蚁都在蚁穴A处，并等概率地向B、C、D处前行，随后在各节点继续等概率向前前行直到H，随后再由信息素含量控制蚂蚁在A点和H点之间运动。节点之间的连线表示路径，图中数字代表路径长度。很显然，该路径网络空间中，A-C-E-H是一条最优路径，而A-B-F-H和A-D-G-H是该空间的次优解。

1.3 拓扑空间局部损坏

本文中，我们采用蚁群优化算法，重点考察该空间拓扑结构发生局部改变或出现缺损时，对蚁群寻找最佳路径的影响。研究过程中，利用两个矩阵记录两类信息：一个记录两个节点之间的距离，另一个则记录各条路径上的信息素量。前者是一个不变的对称矩阵，后者是一个动态的对称矩阵，矩阵的行和列对应位置是连接两条节点的道路信息，两个节点没有连接或者连接同一节点时，对应矩阵元设为0。

(4)

图1是整个蚁群路径空间的结构模型，经过蚁群搜寻一段时间后，所得的解其中包含最优解、次优解和一般解。所以，为简化计算过程，本文先从简化的蚁群模型中进行模拟计算。矩阵中各元素对应的节点是从左到右分别为A、B、C、D、E、F、G、H，对于蚁群简化模型其道路矩阵为(4)。如果蚁群在寻找食物过程中，CE道路被破坏，路径空间发生变化，这时从A出发的蚁群会考虑选择其它替代路径。蚂蚁的数量取得适中，如果蚂蚁数太少，则初始信息数分布对结果有很大影响，如果蚂蚁数太多，则运行时间会增长。本文中，我们设置蚁群总共有250只蚂蚁，单位路径长度为1，初始道路信息素为0。蚁群搜寻一段时间后，局部路径CE处被破坏，记录此时信息素的含量。然后，蚂蚁搜寻新的替代路径，构建出新的路径空间，运行1000个时间单位后记录相应各路径上的信息素量。

1.4 模拟结果

通过蚁群算法模拟计算，记录图1所示路径空间中搜寻的结果。为简单起见，矩阵中各元素值用该路径上信息素与最大信息素的比来表示。路径空间破坏前后的蚁群搜寻结果有三种情形：(1) 正常路径空间情形；(2)蚁群短时搜索后局部路径被破坏情形；(3)蚁群长时搜索后局部路径的破坏及重构。下面分别加以讨论。

(1) 正常路径空间情形

路径空间处于正常状态时，蚂蚁搜索一段时间后，遗留在路径上的信息素分布如图2所示。可以看出，图2实际上是蚁群搜寻过程的一个中间结果。即蚂蚁通过一段时间的搜索后，逐步选中了三条路径，其中，以ACEH这条路径为最优路径，另外两条为次优路径。随着搜索过程的进行，遗留在ABFH,ADGH两条路上的信息素逐渐降低直至为零，而在中间那条上的信息素则变得最大，表明所有蚂蚁最终选择了ACEH作为最佳路径。

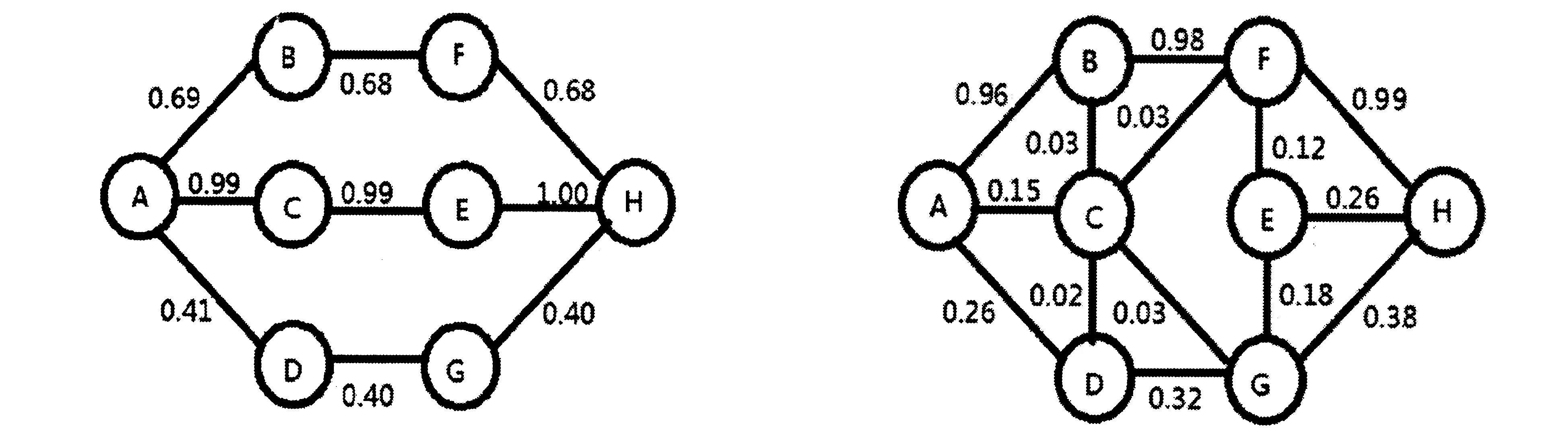
图2 三条主要路径上的信息素分布 图3 搜索过程开始后不久，局部路径CE即断开，稳定后信息素的分布示意图Fig.2 The pheromone distribution on the three main paths Fig.3 The distribution graph where the pheromone reaches a steady state after the local path CE is disconnected shortly during the search process.

(2)蚁群短时搜索后局部路径被破坏情形

按照上述搜寻方案进行模拟，当蚁群搜索过程进行较短时间后，局部路径C-E就遭到了破坏。然后让蚁群继续进行搜索，可以发现，蚂蚁会寻找替代路径重构空间。继续搜寻一段时间后，相应各路径上的信息素分布如图3所示。

由于局部路径C-E断开，导致蚂蚁重新寻找新的路径，这样从A出发的后续蚂蚁就会重新评估A-B, A-C和A-D这三条路径的优劣了。因此，较多的蚂蚁会逐步舍弃A-C这条路径，而改走A-B和A-D这两条。随着时间的推移，已抵达C、E两点的蚂蚁会沿外围的路径寻找,在此基础上，蚁群继续进行搜索行动，最终结果选择了A-B-F-H这条路径。

(3) 蚁群长时搜索后局部路径的破坏及重构

当蚁群搜索较长一段时间后，搜索结果快接近稳定状态了，绝大部分蚂蚁都集中在最优解ACEH这条道路上，相应的路径上信息素的含量也非常高，而次优解路径上的蚂蚁信息素即将挥发殆尽,结果如图2所示。此时若局部路径CE遭到破坏，那么结果会是什么样的情形呢？

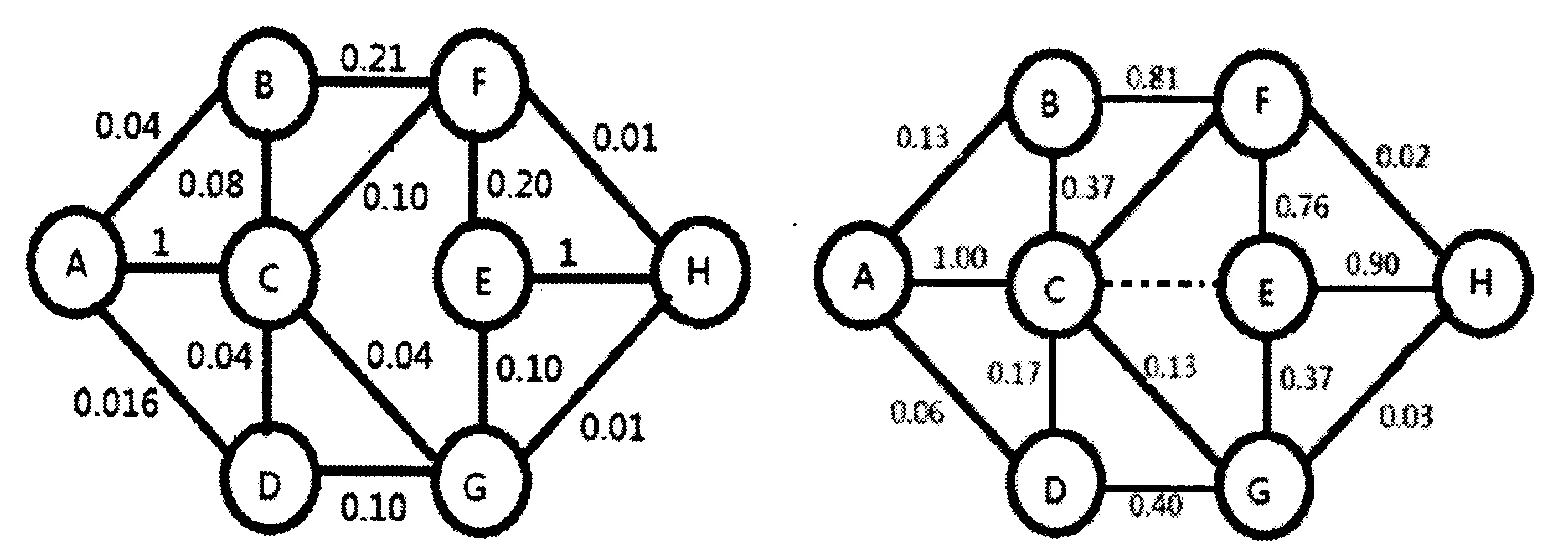
图4a 蚁群搜索较长一段时间后，局部路径CE被破坏时蚁群道路上的信息素分布示意图。图4b 蚁群在局部路径CE被破坏，继续搜索一段时间后信息素的分布示意图。图中显示有两条较好路径可供选择：一条路线是ACBFEH,另一条路线是ACDGEH。Fig.4a The pheromone distribution on ant colony road following ant colony search for a long time and local path CE is destroyed.Fig.4b The distribution diagram of pheromone after the local path CE is destroyed and continues searching for a period of time. Two better paths could be chosen from: the red ACBFEH and the blue ACDGEH.

图4a是路径CE刚被冲毁时各路径上信息素浓度分布示意图。若让蚁群在此基础上继续进行搜索，直至找到最终路径，记录相应的蚁群数量和信息素分布情况并进行分析，我们发现，蚁群搜索路径与上述两种情形完全不同，所得结果如图4b所示。从图中信息素的分布情况可以看出，当局部路径CE被破坏后，蚁群就近寻找替代路径，初始阶段选择ACBFEH和ACDGEH作为较好路径，随着时间推移，最终蚁群选择出ACBFEH这一条最佳路径。

2 结果分析与讨论

现对上述结果进行简要分析。对于第一种情形：路径空间没有被破坏，在搜寻过程中，利用蚁群算法，蚂蚁很快会从众多的路径中筛选出较好的三条：ABFH, ACEH, ADGH，从遗留的信息素浓度高低也可比较出这三条路径的优劣：ACEH>ABFH> ADGH。全体蚂蚁更新信息素后，在此基础上继续搜索和对比，所有蚂蚁最终选择了ACEH作为最佳路径。

对于第二种情形，蚂蚁搜寻过程开始不久，局部路径C-E就断开，此时，由于处于搜寻过程的初期，各条路径上遗留的信息素浓度都低，特别是中间路径ACEH上信息素相比其它路径而言，并没有形成优势。因此，一旦CE中断，从A出发的后续蚂蚁就会重新评估A-B, A-C和A-D这三条路径的优劣了。这样一来，较多的蚂蚁会慢慢舍弃A-C这条路径，而改走A-B和A-D这两条。并且随着时间的推移，围绕C、E两点周边路径的蚂蚁就慢慢沿外围路径寻找。蚁群继续进行搜索，最终选择了A-B-F-H这条路径，结果如图3所示。

对于第三种情形，蚁群搜索较长时间后路径空间才被毁坏，由于长时间的搜索，蚁群搜索的结果已经定型，基本确定了A-C-E-H作为最佳路径，分布在该条上的蚂蚁和信息素比其他路径上要高得多。因而，此时局部路径C-E断开的话，聚集在C和E两点附近的蚂蚁会就近寻找替代路径，而不是从C点沿C-A返回蚁穴后再重新寻找。这时有CB,CF, CG和CD四个可能的方向供选择。比较这四个方向路径的优劣，其中CBFE、CDGE是较好的替代方案, 因而找出ACBFEH和ACDGEH两条可能的较优路径(如图4所示)，并最终选定ACBFEH路径为最佳方案。

在这种情形下，与第二种情形的结果明显不同，蚁群最终所选的最佳路径是ACBFEH, 而不是ABFH，对比路径长度，似乎蚁群选择的不是最优路径，这是什么原因造成的呢？我们可以从图4所示的拓扑结构的子空间来寻找答案。当CE被破坏之前，蚁群经过较长时间的寻找，借助于信息素的交流与沟通，毫无疑问会确定ACEH为最佳路线，但是，一旦CE被阻断，蚂蚁会就近寻找出路，而由于此时附近的CB等路径上仍然遗留有一定浓度的信息素，提示聚集在C点处的蚂蚁围绕CE沿着局部子空间CBFE或CDGE寻找。最终找出的路径为ACBFEH，这实际上是由原来全局最优路径的一部分AC与EH，与当前局部最优子空间CBFE有机组合起来的结果。

3 结论

在本文中，首先构建一个蚁群搜寻食物的空间结构，蚂蚁从蚁穴出发有多条路径可以寻找到食物，我们利用蚁群优化算法设置一定数量的蚂蚁进行寻找。模拟结果发现，当路径不存在局部毁损情况时，蚂蚁所找路径为通常全局最优的ACEH。若寻找过程中在最优路线上出现局部毁坏，则会使得蚂蚁重新构建新的路径。这时所寻找的路径有两种情形：其一，当出现毁坏是在搜寻过程进行较短时间后发生，则蚁群重新找到的路径即为正常情况下的次优解。其二，若毁坏是在搜寻较长时间后发生，则蚁群所找的路线是将全局最优路径的部分路段和局部子空间中的最优路段综合起来的结果。

本文模拟结果告诉我们，一方面，利用蚁群优化算法，可以寻找出存在局部空间结构出现毁损时的最优路径，重构出新的拓扑空间。另一方面，利用这种现象可分析和判断网络空间中的故障所在。例如，对于神经元网络或通讯网络，若某个局部出现故障，则会使得其周围的线路出现电流突然变化或信息突然拥堵等现象，监控这些现象就可以快速定位和排查神经网络中的病变或电力网络中的故障所在。

[1] DORIGO M, BLUM C. Ant colony optimization theory: A survey Theory[J]. Comput Sci， 2005，344(2-3):243-278.

[2] FORSATIA R, MOAYEDIKIAA A, JENSENC R, et al. Enriched ant colony optimization and its application in feature selection[J]. Neurocomputing, 2014(142):354-371.

[3] AKPINAR S. Hybrid large neighbourhood search algorithm for capacitated vehicle routing problem[J]. Expert Syst Appl, 2016(61):28-38.

[4] CAI J J, LI Q, LI L X, et al. A fuzzy adaptive chaotic ant swarm optimization for economic dispatch[J]. Int J Electr Power Energy Syst, 2012(34):154-160.

[5] LIU L Z, ZHANG J Q, XU G X, et al. A modified chaotic ant swarm optimization algorithm[J]. Acta Phys Sin, 2013(62):170501-1-6.

[6] LIU L Z, ZHANG J Q, XU G X, et al. A chaotic secure communication method based on chaos systems partial series parameter estimation[J]. Acta Phys Sin, 2014(63):010501-1-6.

[7] LI L X, PENG H P, WANG X D, et al. Comment on two papers of chaotic synchro- nization[J]. Phys Lett A, 2004(333):269-270.

[8] LISSOVOI A, WITT C. Runtime analysis of ant colony optimization on dynamic shortest path problems[J]. Theor Comput Sci, 2015(561):73-85.

[9] ZHANG J Q, HUANG S F, PANG S T, et al. Optimizing calculations of coupling matrix in Hindmarsh-Rose neural network[J]. Nonlinear Dynamics, 2016，83(3):1303-1310.

[10] JIANG K L, LI M A, ZHANG H W. Improved Ant Colony Algorithm for Travelling Salesman Problem[J]. Journal of Computer Applications, 2015，35(S2):114-117.