多参数布朗运动驱动的随机微分方程解的存在性
2018-03-23何世峰
何世峰
(合肥职业技术学院,安徽 巢湖 238000)
众所周知如下随机微分方程:
(1)
在飘逸系数b和扩散系数σ满足 Lipschitz 或局部 Lipschitz 条件以及线性增长条件下,方程存在唯一强解。一些学者致力于降低b或σ所满足的条件以得到 (1) 解的存在唯一性或存在性,这方面的工作可见 Protter[7]与 Krylov[5]。特别地, Barlow[1]指出当σ仅仅满足连续性假设的条件下,(1) 不存在唯一解。因此,就有必要来降低对b的连续性的要求。基于此,Halidias和 Kloeden[4]利用上下解的方法给出了当σ满足Lipschitz条件,b满足某种非连续性条件下方程 (1) 解的存在性结论。当我们考虑一类开关系统受到白噪声影响时,就会出现如下具有不连续飘逸系数的随机微分方程:
dXt=H(Xt)dt+dWt,其中H:R→R为由下式定义的一个Heaviside函数:
H(X):={0,x<0,1,x≥0。
此外,首先Cairoli[2, 3]给出如下由多参数布朗运动驱动的随机微分方程:
(2)

然而在[2,8,9,10]中,解的存在性都要求b具有连续性。本文主要讨论当d≥3时在b满足某种单调非连续性条件以及满足σ某种非Lipschitz 条件下给出 (2) 解的存在性。为此,利用截断和罚则函数法给出了非 Lipschitz 条件下方程解的比较性定理。 最后利用 Lipschitz 函数逼近的方法给出了连续性飘逸系数满足线性增长条件下解的存在性定理。
1 记号和预备知识

zz′(或)z≼z′当且仅当或
以λ(·)表示Lebesgue测度,WA,A∈β([0,1])d表示随机实值Gaussian可加集值函数满足:
EWA=0,EWAWB=λ(A∩B)。
对于任意的z,z′∈T,以 (z,z′] 表示矩形集{z″∈T:zz″≼z′}而以(z,z′)表示矩形集 {z″∈T:zz″z′}。此外,称具有连续轨道的过程Wz:=W(0,z]为多参数布朗运动。对于任意的z∈T,以Fz表示{Wz′,z′≼z}在P下的完备化。因此,在上述偏序意义下{Fz,z∈T}构成为F的一个增子σ-代数。进一步地,对于z″z′z,W(z′,z]与Fz″是独立的。记并以S2表示Fz-适应的满足条件|X|S2=|X*|L2<∞的过程所构成的集合,其中L2=L2(Ω,R)。由此可见,(S2,|·|S2)是一Banach空间。
为得到本文的主要结论,给出几个假设条件。 对于x,y∈Rn有:
(H1) |b(x)-b(y)|2≤ρ1(|x-y|2);
(H2) |σ(x)-σ(y)|2≤ρ2(|x-y|2)

注1 (1)为说明结论的一般性,给出具体的有关ρi(·),i=1,2的例子,设δ∈(0,1)为充分小的一个常数。
定义ρi(u)=Ku,u≥0,i=1,2,
(2)由于ρi(u)为凸的并且满足ρi(0)=0,我们可以找到一对正常(ai,bi)满足
ρi(u)≤ai+biu
(3)
对于i=1,2都成立。
引理2([10]) 在(H1)和(H2)下,(2)存在唯一Fz-适应的连续解。
本文首先考虑方程(2)解的比较定理。为此,考虑如下两个随机微分方程:
(4)
(5)
假定对于任意的x∈Rn,x≤y以及b1(x)≤b2(x),我们有如下的比较定理:

证假设b2满足(H1)。通过截断和罚则函数法定义如下函数:
则易知|p(x,y)-p(x,y)|≤|y-z|以及r(·)满足Lipschitz条件。考虑如下随机微分方程:

(6)
则其系数满足条件(H1)和(H2)。引理2表明(6)存在唯一解不妨记为Yt。
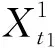


以此,如果b1满足条件(H1),则定理结论同样成立,只需在证明过程中略微地变化即可。
2 不连续飘逸系数下解的存在性

(7)
则易知Xn为单增序列,往证Xn在S2范数下为有界的。
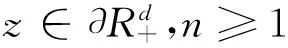
(8)


由注1(2)以及b的线性增长性,可知
其中a,b为两个正常数,由此,


定理5设b为单调增加、左连续满足线性增长条件而σ满足条件(H2),则(2)至少存在一个解。
证由定理3可知(Xn)为单增序列,引理4表明(Xn)在S2中是有界的,由控制收敛定理可知Xn在S2中为收敛的。记X为(Xn)的极限过程。由此,对几乎所有的ω,有
(9)

(10)
从而对几乎所有的ω以及对于z,
(11)
由σ以及随机积分的连续性,有
(12)
再者由于Xn为单增的,故上述收敛在p-a.s.意义下也是成立的。易证Xn→X的收敛性。故在(7)的两端取极限,可知(2)解的存在性。
3 连续飘逸系数下解的存在性
本段则采用Lipschitz函数逼近的方法给出b满足连续和线性增长条件下(2)解的存在性结论。对于满足连续线性增长条件的函数,有如下的逼近性结论:
引理6([6]) 设b为满足连续线性增长条件的函数。 定义bn(t,y)=inf{b(t,q)+n|y-q|:q∈Q,则对于n>C,bn有:
1、线性增长性:|bn(x)|≤C(1+|x|);
2、单调性:bn(x)↑b(x);
3、Lipschitz条件:|bn(x)-bn(y)|≤K|x-y|;
4、强收敛性:如果xn→x,则有bn(xn)→b(x)。
(13)
由比较定理可知Xn为单增序列。往证Xn收敛到(2)的解X。
(14)
其证明的主要思路同引理4。故在此略去。本文第二个结论为:
定理8在b满足线性增长以及σ满足条件(H2)条件下,(2)存在解。
其证明思路同定理5。
[1] BARLOW M. One-dimensional stochastic differential equations with no strong solution[J]. J London Math Society Second Series, 1982,26(2):335-347.
[2] CAIROLI R. Une inegalite′ pour martingale `a indices multiples et ses applicatios, in Seminaire de Probabiliti′e[J]. Lect Notes in Math Berlin, 1970(124):1-27.
[3] CAIROLI R. Sur une ′equation differentielle stochasticque[J]. C R Acad Sci Paris Ser A, 1972,274(1):1173-1742.
[4] HALIDIAS N, KLOEDEN P. A note on strong solutions for stochastic differential equations with discontinuous drift coefficient[J]. J Appl Math Stoch Anal, (2006)article ID (73257):1-6, doi: 10.1155/JAMSA/2006/73257.
[5] KRYLOV N V. On weak uniqueness for some diffusions with discontinuous coefficients[J]. Stoch Proc Appl, 2004,113(1):37-64.
[6] LEPELTIER J P, SAN MARTIN J. Backward stochastic differential equations with continuous coefficients[J]. Stat Prob Letters, 1997,32(4):425-430.
[7] PROTTER P. Stochastic integration and differential equations[M]. Berlin: Springer, 1990.
[8] REID J. Estimate pn moments of the solutions to stochastic differential equations in the plane[J]. Ann Prob, 1983,11(3):656-668.
[9] YEH J. Existence of strong solutions for stochastic differential equations in the plane[J]. Pacific J Math, 1981,97(1):217-247.
[10] ZHANG X, ZHU J. Non-Lipschitz stochastic differential equations driven by multi-parameter Brownian motions[J]. Stoch Dyna, 2006,6(3):329-340.
