不同进口条件对OGV/前置扩压器流场大涡模拟结果的影响
2018-03-23李井华颜应文
张 腾,李井华,颜应文
(南京航空航天大学能源与动力学院,南京210016)
0 引言
航空发动机燃烧室中燃气的高效稳定燃烧要求气流在燃烧室进口通过扩压器进行减速扩压且尽量减小气流的压力损失,因此压气机与燃烧室交界处的气动力学优化对燃烧室设计尤为重要。国内外学者对压气机出口导向叶片的尾迹结构与前置扩压器的湍流流场特性的相互影响进行了深入的试验研究和CFD模拟。Walker等[1]试验研究发现与传统设计方法相比,OGV/前置扩压器一体化的设计方法可以改善燃烧室进口的空气动力学特性,增大扩压器面积比,提高静压恢复系数并减小总压损失;徐磊磊等[2]通过试验与数值计算相结合的方法研究了不同扩张角下前置扩压器性能的变化,发现前置扩压器的扩张角存在最佳值,扩张角大于该值时气流会出现流动分离;LI等[3]采用不同RANS湍流模型对OGV/前置扩压器的流场特性进行数值研究,结果表明虽然RANS模型能够合理地预测出整体的流动结构和性能,但却无法正确预测出OGV的流动,尤其是导向叶片附面层上所发生的流动,因此采用大涡模拟(Large Eddy Simulation,LES)进行初步计算,但由于LES进口速度场中没有叠加任何脉动,所预测的吸力面上有较大的流动分离。
采用LES模拟湍流流动时如何生成符合湍流统计特性的进口条件,一直是学者们研究的重点。目前最简单的方法是在进口的速度场加入随机脉动,如白噪声(White noise,WN)[4],但这种方法生成的进口速度场没有任何的时间-空间关联性,而且在下游会很快耗散掉。近年来,为解决这个问题,许多学者提出不同方法。Batten等[5]采用傅里叶合成方法得到较为真实的湍流脉动能谱,并考虑到近壁面流动的各向异性,但是在进口下游较长的一段距离后才能发展为真实湍流;Lund等[6]提出预前模拟(Precursor simula-tion)的方法,通过在进口前加入独立的计算区域,并对其进、出口采用周期性边界条件,以此生成充分发展的湍流流动瞬态速度场,并通过重整(rescaling)的方式将瞬时脉动加入到LES进口条件中,但是该方法需要单独的计算域,所需的计算成本较高;Jarrin等[7]提出1种新的合成涡方法(Synthetic Eddy Method,SEM),所需计算成本较少,适用于任意进口几何形状与流动情况,且所需的信息较为简单,在进口下游发展为实际湍流所需长度较短。合成涡方法在槽道流动[7-9]、后台阶流动[7]、机翼绕流[10]等简单流动中都得到应用;对于具有复杂几何结构的流场,国内近年也开始进行相关研究,如杨帆等[11]采用合成涡方法生成湍流进口边界条件,对强旋流预混火焰进行大涡模拟研究。
本文在已有试验测得的进口统计数据的基础上[12],分别加入白噪声与合成涡的方法生成进口条件,采用大涡模拟方法数值计算OGV/前置扩压器的流场特性,分析不同进口条件对数值模拟结果的影响,并与试验结果进行对比。
1 数学模型
1.1 LES亚网格模型
湍流流动由不同尺度的漩涡组成,其中大尺度涡旋对流动影响较大,而小尺度涡旋则主要起耗散作用。因此,可以采用大涡模拟对于大尺度的可解分量通过控制方程直接求解,对于小尺度结构可通过亚网格模型化求解。
本文采用Smagorinsky亚网格尺度模型[13],将亚网格雷诺应力模化为

式中:μt为亚网格黏性,可写为
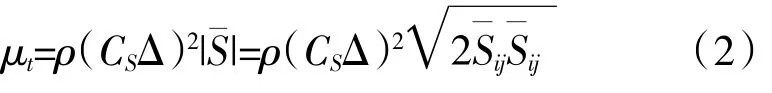
式中:Cs为模型常数,对于内部流动一般取0.1;Δ为滤波尺度,取为过滤后的应变率张量。
同时在近壁面区域引入Van Driest[14]近壁阻尼函数减小近壁面的涡黏性。
1.2 合成涡方法(SEM)
合成涡方法可以高效便捷地生成进口脉动速度场,该方法假设脉动速度由进口平面附近空间B内随机分布的N个涡共同作用产生。由这N个涡产生的速度表示为
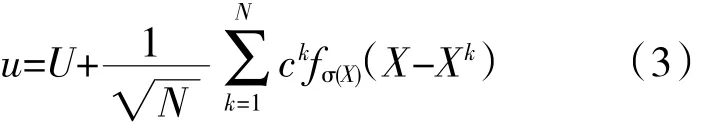
式中:U为进口平均速度场,由试验测得或由RANS结果得到;Xk为N个涡的空间位置坐标;ck为涡的相对强度,定义为

式中:aij为雷诺应力Rij的Cholesky分解[10];ε为独立随机变量,以相等概率取-1或1

fσ(X)(X-Xk)为处在Xk位置的涡附近的速度分布函数
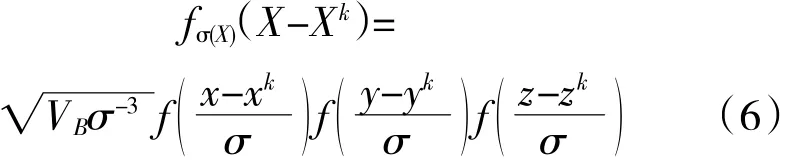
式中:σ为涡的特征尺度,由湍动能、耗散率、网格尺度共同决定[15];f为形函数,定义为
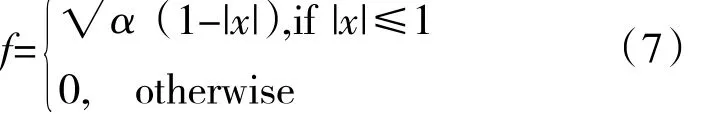
式中:α为形函数系数,为保证脉动速度与试验测量值准确符合,本文取α=1.61256。
每个迭代时间步,第k个涡的位置为
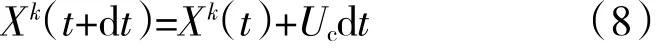
式中:Uc为涡的运动速度,其值一般取进口平面的平均速度。由此保证了每个时间步的脉动速度场与上一时间步的时间关联。
应用合成涡方法生成进口脉动速度场的步骤为:
(1)在已知进口各输入量(如平均流场、雷诺应力分布等)的基础上,确定进口平面附近涡的运动空间B;
(2)随机生成每个涡的位置Xk和脉动强度ε;
(3)计算由N个涡合成的脉动速度并叠加到进口平均速度场中;
(4)涡在空间B中以平均速度Uc运动;
(5)对运动到空间B外的涡,在相对的面上重新生成新的位置Xk和脉动强度ε。重复步骤(3)~(5)。
2 研究对象
本文研究对象为压气机出口导向叶片与前置扩压器组合结构,如图1所示。OGV叶栅平均半径为375 mm,高度h=36.6 mm,全环OGV叶栅包含160个弦长为39 mm的直叶片。IGV(进口导向叶片)叶栅包含80个叶片,为考虑IGV尾迹对OGV/前置扩压器中流场的影响,数值模拟取2个OGV叶片,角度为4.5°。前置扩压器进、出口面积比为1.6,长度L=2.33h。

图1 压气机出口导向叶片与前置扩压器组合结构
计算域和计算网格如图2所示。采用RR公司网格生成程序PADRAM[16]生成结构化分块网格,OGV区域流向和展向的无量纲网格步长分别为Δx+≈25、Δz+≈40,叶片附近第1层网格Δy+≈1;扩压器区域流向的无量纲网格步长为Δx+≈100,展向网格步长对OGV尾迹区域内为Δz+≈8,尾迹区域外为Δz+≈20,壁面附近第1层网格高度Δy+≈5。网格总量约为900万,利用自编软件DELTA并行计算。在计算域的周向上采用周期性边界条件;内、外环壁面及叶片壁面采用无滑移壁面边界条件;进口平均速度为45 m/s(Ma=0.13),其方向与进口平面法向呈45°,进口在试验测得的2维速度分布的基础上,分别采用加入白噪声与合成涡方法生成脉动速度场,进口温度和压力与试验环境的相同,分别为288 K、101325 Pa;出口采用零梯度出口边界条件。时间步长为1×10-6s,稳定后取3个流通时间的时间段计算平均流场。

图2 OGV/扩压器结构化分块网格
3 计算结果及分析
3.1 合成涡方法生成进口条件
本文将试验测得的OGV进口平均速度场、脉动均方根分布、湍动能、耗散率分布作为合成涡方法的输入信息。在计算aij时取
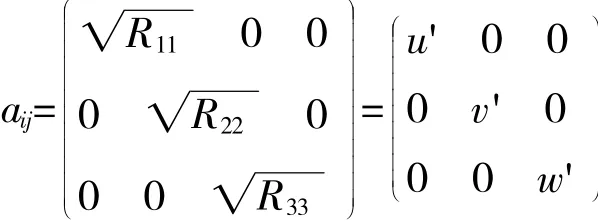
式中:u',v',w'分别为试验所测得的3个方向上的脉动均方根。
采用2种方法所生成的脉动速度场的统计平均如图3所示。从图中可见,采用2种方法所生成的时均轴向U和周向V速度均与试验结果高度契合,而径向速度W由于数值较小,受计算误差影响稍大,但分布趋势与试验测量基本符合。采用2种方法所生成的速度场的脉动均方根分布如图4所示。从图中可见,采用White noise方法生成的脉动均方根远远大于试验值,并不满足进口湍流的统计特性;而采用SEM方法产生的3个速度分量的脉动均方根与试验结果十分吻合,在近壁湍动能较大处稍有偏差,但误差最大不超过4%。

图3 OGV进口周向平均时均速度沿径向分布
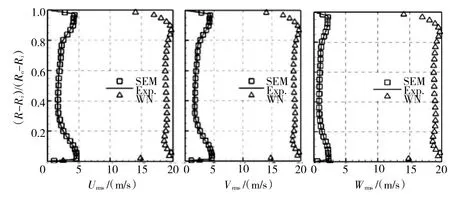
图4 OGV进口周向平均脉动均方根沿径向分布
进口中心点速度能谱如图5所示。从图中可见,在频率小于10 kHz范围内为大尺度含能区,在频率为10~12 kHz范围内满足湍流理论中的惯性子区-5/3律,在频率大于12 kHz时也出现了湍流理论中迅速衰减的耗散区。
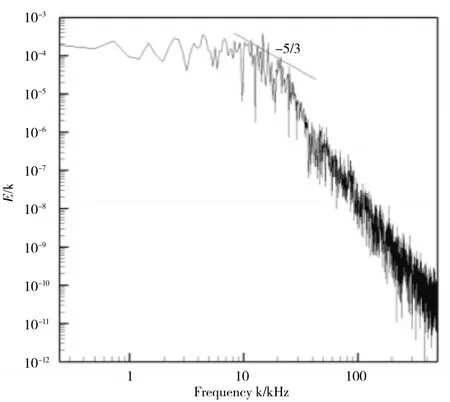
图5 进口面上中心点A轴向瞬时速度能谱
从上述结果可见,合成涡方法产生的瞬时速度场的统计特性能够满足目标要求,平均速度场即为目标进口平均速度场,雷诺应力满足目标进口雷诺应力分布要求。
3.2 流场结果分析
引入速度梯度张量的2阶不变量Q准则[17]
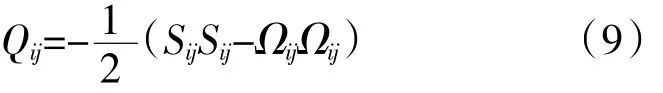
Q取决于应变率张量Sij与转动张量Ωij之间的关系。Q准则可以用来评价所求解的湍流中的拟序结构。在2种进口条件下OGV/扩压器中部Q准则等值面如图6所示。从图中可见,SEM方法中可以观测到进口流动中的3维湍流结构,而在White noise方法中为不相干的小尺度湍流结构且很快耗散掉。SEM方法生成的湍流结构在下游由于叶片前缘的层流化而消失,但在叶片表面下游会再次出现,White noise方法中也会在下游再次出现湍流结构,但SEM方法出现得较早。同时在扩压器中可以看到导向叶片尾迹的复杂湍流结构。
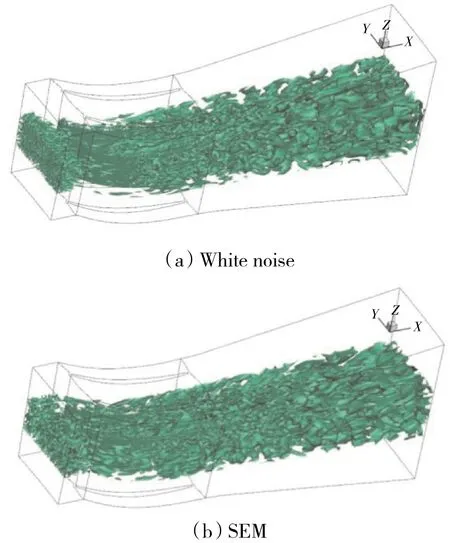
图6 中心高度处Q=1000等值面
距离OGV吸力面壁面约0.2 mm处的时均轴向速度如图7所示,从图中可见,在2种进口条件下,气流到达叶片前缘并滞止,随后在叶片吸力面上经历了层流化过程、加速、层流到湍流的转捩及附面层的分离再附着。虽然流动过程相似,但很显然SEM进口方法预测的吸力面上的分离区要小,由于受测量方法的限制,在试验中并没有相关的叶片吸力面分离区的数据。同时在这一流动分离区域附近产生较大应力,从而导致尾迹在叶片尾缘处分离并在下游迅速混合。从图中还可见,叶片前缘后的流动跨度较大,由于通道内、外壁面边界层与叶片的相互作用,以及叶片前缘后空气的加速,使得靠近叶片内、外端壁处形成2个动量较低的区域,且该区域不断扩大并在叶片尾缘处形成2个分别靠近内、外端壁的低动量“包”。

图7 叶片吸力面时均轴向速度分布
SEM方法中通道中心高度截面处瞬态轴向速度与径向速度分布如图8所示。从图中可见,来自叶片吸力面和压力面的气流在叶片尾缘处交汇并相互作用,使尾迹在扩压器中的不稳定混合掺混,并在趋近扩压器出口时逐渐均匀。
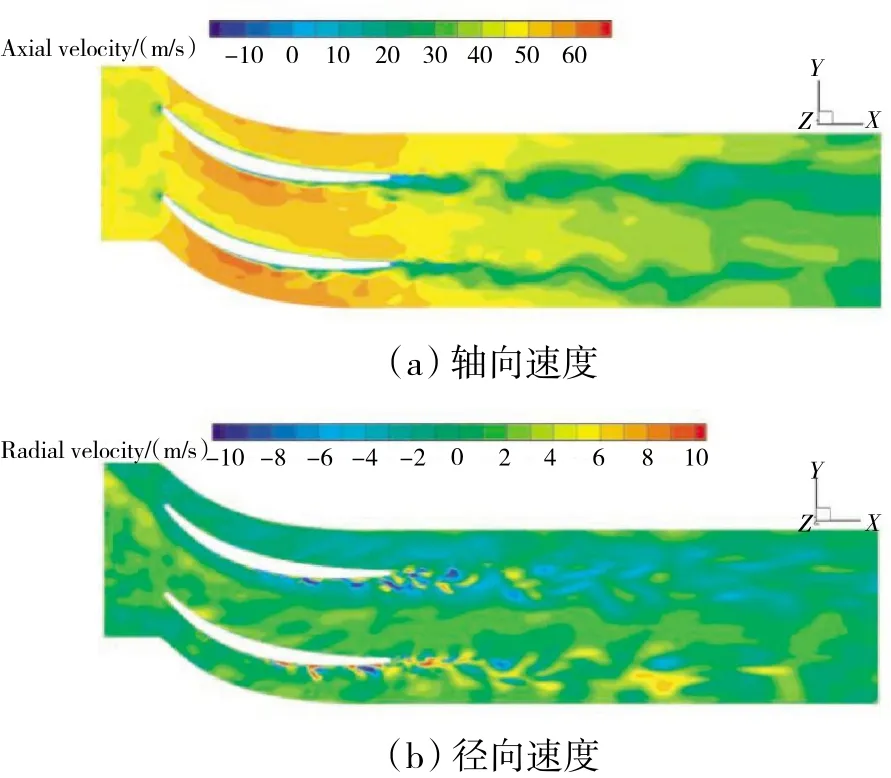
图8 中心高度处瞬态轴向速度与径向速度分布(SEM方法)
扩压器出口截面上的时均轴向速度的分布如图9所示。从图中可见,与试验结果相比,计算预测结果捕捉到扩压器出口的速度分布趋势,OGV尾迹由于混合作用在扩压器出口截面已经趋向均匀,但仍能明显看出其影响痕迹;2个明显不同的高速度区分别对应上游的2个OGV叶片通道,而其不同则体现上游IGV尾迹对下游的影响(2个OGV叶片对应1个IGV叶片);在扩压器逆压力梯度的作用下,气流经过扩压器后减速增压,可能导致在出口壁面处发生流动分离,二次流也导致在2个加厚的尾迹区与壁面边界层之间产生低动量区,很明显无论是数值计算还是试验都没有检测到流动分离。
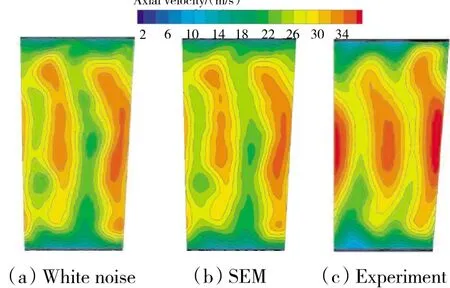
图9 扩压器出口时均轴向速度分布
OGV出口截面轴向速度沿周向平均的径向分布如图10所示。从图中可见,2种方法所预测的速度分布大致相同,与试验数据相比,在中间高度处速度分布符合得很好,但在近壁面处稍有误差。
前置扩压器内某截面(x/L=0.442)和出口截面(x/L=1.0)轴向速度沿周向平均的径向分布如图11所示。从图中可见,采用2种方法得到的分布曲线与试验结果的分布趋势相同,但在内壁面附近与通道中间高度处符合较差,与试验值相比,预测结果分布较为平缓。部分原因是在试验中测量IGV出口速度时布置的测点有限,在数值模拟时需要对试验测得的2维速度场插值作为进口平均流场,可能无法完全反映IGV出口流场特性,由此在计算中对下游流场产生一定影响。
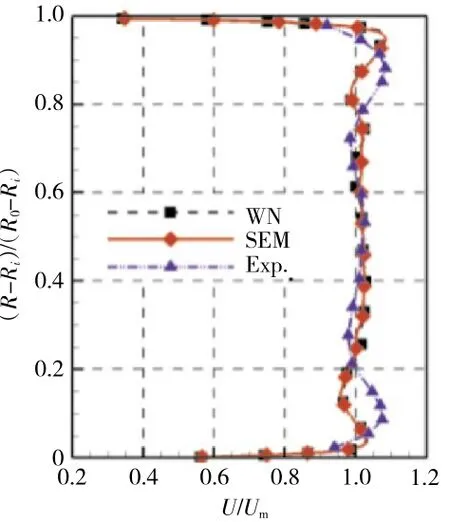
图10 OGV出口时均轴向速度周向平均沿径向分布
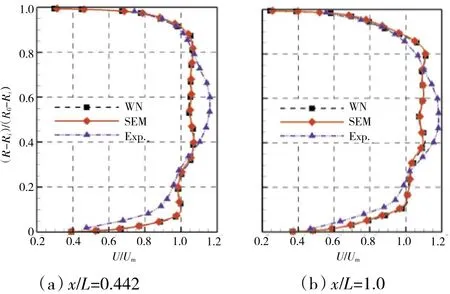
图11 扩压器内不同位置时均轴向速度沿周向平均的径向分布
4 结论
本文对1种OGV/前置扩压器组合结构的流场性能进行大涡模拟数值研究,分别采用白噪声与合成涡方法生成进口条件,研究不同进口条件对数值模拟结果的影响。得到如下结论:
(1)采用合成涡方法所生成的进口脉动速度场的时均速度分布和脉动均方根分布与试验结果十分符合,速度能谱分布符合湍流经典理论。与白噪声方法相比,合成涡方法在进口下游产生的湍流结构不会立即耗散掉,可传播到下游较远处。
(2)与白噪声方法相比,合成涡方法在吸力面上预测的分离区较小。
(3)在OGV出口、扩压器内及扩压器出口截面,采用2种方法所预测的速度分布相差不大,与试验结果相比,分布趋势相同,但在内壁面附近与通道中间高度处符合较差。
