基于保护映射理论的航空发动机LPV/PI控制
2018-03-23叶志锋肖玲斐
周 黎,叶志锋,肖玲斐
(南京航空航天大学江苏省航空动力系统重点实验室,南京210016)
0 引言
航空发动机是1个强非线性复杂系统,在范围宽广的飞行包线内工作时,其工作状态随外界变化而不断变化[1]。传统非线性系统的控制方法为变增益控制方法,其基本思想是对非线性模型中的一些稳定设计点进行线性化以获得对应各点的线化模型,然后针对各线化模型分别设计控制器,运用拟合或切换的方法将各控制器联系起来[2]。在传统变增益控制器的设计过程中,每个设计点设计的控制器都能满足控制系统的性能要求,但是难以保证系统的全局控制性能[3]。同时传统变增益控制方法对所选取的设计点数量依赖程度较大,由于所选取的设计点数目越多,控制效果越好,采用这种控制器的设计过程工作量较大。目前,航空发动机控制方法的研究成果较多,但在工程实践中,应用最多的仍是原理简单、可靠性高和易于实现的 PID(Proportion Integration Differentiation)控制[4]。常用的PID控制器的整定方法有经验法和响应曲线法等,但这些方法仅能使系统在设计点具有较好的动态响应,无法保证整个系统的控制性能。
Saydy等[5]提出的保护映射理论可分析参数化矩阵族和多项式的广义稳定性;文献[6]将保护映射理论首次用在飞机控制系统设计中,通过目标稳定区域的确定来表示飞行操纵品质指标;文献[7]将保护映射理论、LQR技术和遗传算法三者相结合,设计出1种新的控制方法;文献[8]将保护映射理论应用在高超声速飞行器的控制方法设计中,使得高超声速飞行器在大范围包线内工作时能够保持稳定。
本文将基于保护映射理论的控制方法应用于航空发动机控制中,其无需在多个设计点分别进行控制器设计,可通过初始控制器直接获得整个调度参数变化范围内的控制器,能够解决传统变增益控制方法所存在的难以保证全局控制性能问题。
1 航空发动机LPV模型
航空发动机非线性模型

式中:f(g)和g(g)是连续可微的,其LPV模型为
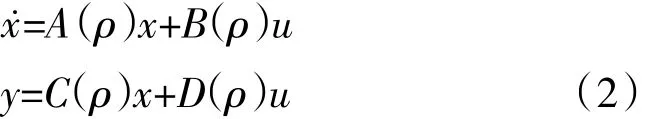
式中:状态向量x∈Rn;输出向量y∈Rm;控制向量u∈Rp;调度参数向量ρ∈Rj,其值随时间变化不断改变;A(ρ)、B(ρ)、C(ρ)和 D(ρ)为系数矩阵,其所有元素与ρ存在函数关系[9]。
研究对象为某型双转子涡扇发动机。所采用的发动机参数均为相似归一化后的相对参数,通过对发动机参数进行相似归一化处理,可以避免因各物理量之间很大的数量级差别而导致建模精度降低。航空发动机为多变量系统,其控制系统存在多个通道。输入量仅选择主燃烧室的供油量增量ΔWf,输出量为高压转子转速增量Δnh,状态变量为低压转子转速增量Δn1和高压转子转速增量Δnh,建立线化模型,并进行控制器设计。航空发动机的主系统加减速仿真主要包括慢车到中间状态加减速、85%转速到中间状态加减速、中间状态到慢车以及到中间状态遭遇加速等过渡过程[10]。在控制器设计时所考虑的发动机状态过程为85%转速到中间状态。
采用的LPV建模方法为雅克比(Jacobian)线性化建模法[11],首先,选择高度H=0 km、马赫数Ma=0的工作点为设计点,高压转子转速nh为调度参数,其变化范围为[0.85,1.05],在该区间采用线性化方法[12]得到不同高压转子转速点的状态变量模型;然后,为提高模型的精确度,将调度参数nh归一化到[0,1]的范围内,即∈[0,1];最后,对状态变量模型的所有系数矩阵进行多项式拟合,拟合后的模型为
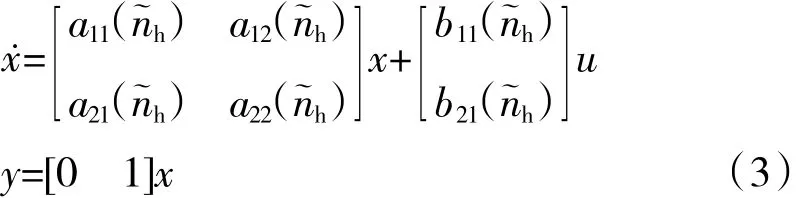
式中:x=[Δn1Δnh]T;u=ΔWf;y=Δnh。
通过大量仿真对比,并综合模型对拟合精度和效率的要求,进行3阶多项式拟合。j=1,2)拟合后为

拟合曲线分别如图1、2所示。从图中可见,拟合存在一定误差,但由于PI控制的强鲁棒性,后续仿真表明其对控制效果的影响较小。
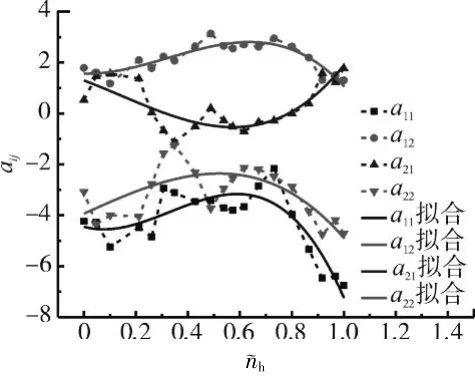
图1 aij的拟合曲线
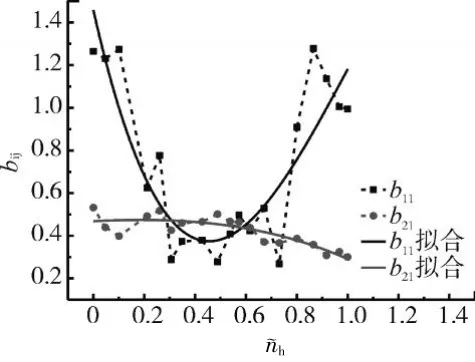
图2 bij的拟合曲线
为了对所建LPV模型进行仿真验证,选择任意2个转速点nh=0.9019和nh=0.9840,LPV模型和非线性模型在相同阶跃输入下,计算得到高压转子转速响应曲线分别如图3、4所示。
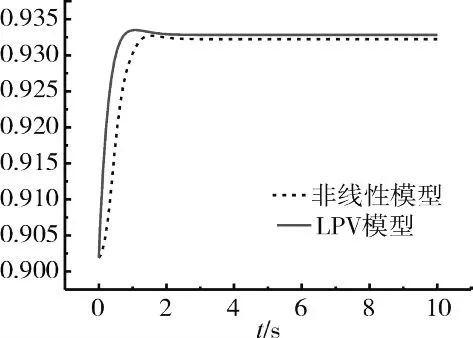
图3 n h=0.9019时模型的高压转速响应曲线
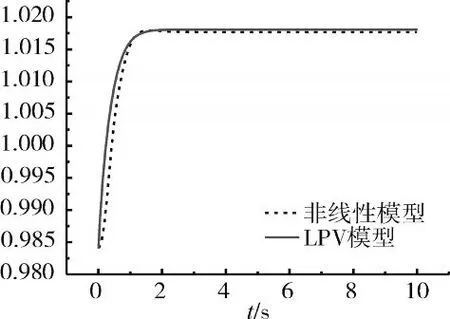
图4 n h=0.9840时模型的高压转速响应曲线
从图3、4中可见,将LPV模型与非线性模型的转速阶跃响应进行比较,跟踪效果较好,虽存在一定的稳态误差,但是稳态误差较小,可利用控制器消除其对控制系统的影响。
2 保护映射理论
矩阵广义稳定性集合S(Ω)定义为
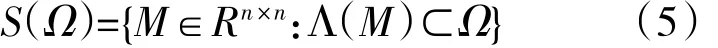
式中:Ω为复平面内的开集;Λ(M)为矩阵M的所有特征值的集合[13];S(Ω)表示所包含的矩阵在Ω区域内保持稳定。
定义1:矩阵Rn×n到复数域C的映射表示为v。∂S表示集合S的边界,如果矩阵M∈∂S(Ω)的充分必要条件为 v(M)=0,则映射 v是 S(Ω)的保护映射,其实质为n×n实矩阵上的标量映射[13]。
保护映射的典型区域如图5所示。
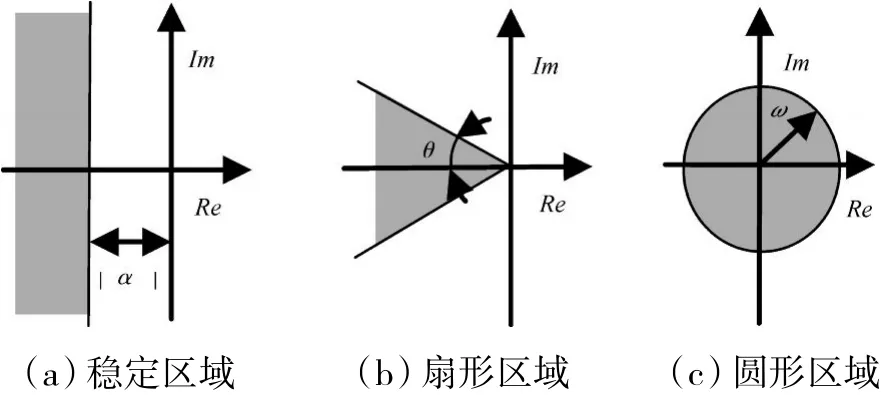
图5 保护映射的典型区域
如图 5(a)所示区域(即 Re(z)<α)的保护映射为
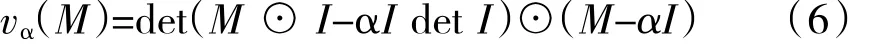
式中:⊙为运算Bialternate积。
如图5(b)所示与虚轴负半轴夹角为θ的2条射线所组成的区域的保护映射为
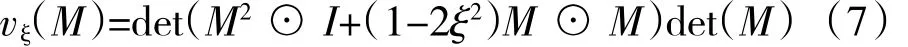
式中:ξ=cosθ。
如图5(c)所示半径为ω的圆形区域的保护映射为
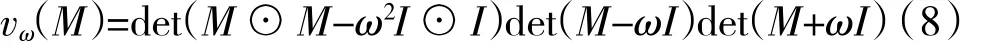
其它区域的保护映射表达式可以根据典型区域通过相关的性质获得,例如:设 S(Ω1),S(Ω2),…,S(Ωh)相应的保护映射为 v1,v2,…,vn,则 S(Ω1∩Ω2…∩Ωh)的保护映射为 v=v1v2…vn。
引理:M(x)=M0+xM1+…+xkMk,表示矩阵多项式,式中:x为未知的参数;Mi为已知的常数矩阵。M(x0)相对Ω区域稳定,vΩ为S(Ω)的保护映射,则根据式(9)、(10)可获得达到控制要求的x最大范围为x∈(x-,x+)[14]

3 参数整定算法
3.1 活动区域定义
不同类型的区域如图6所示。
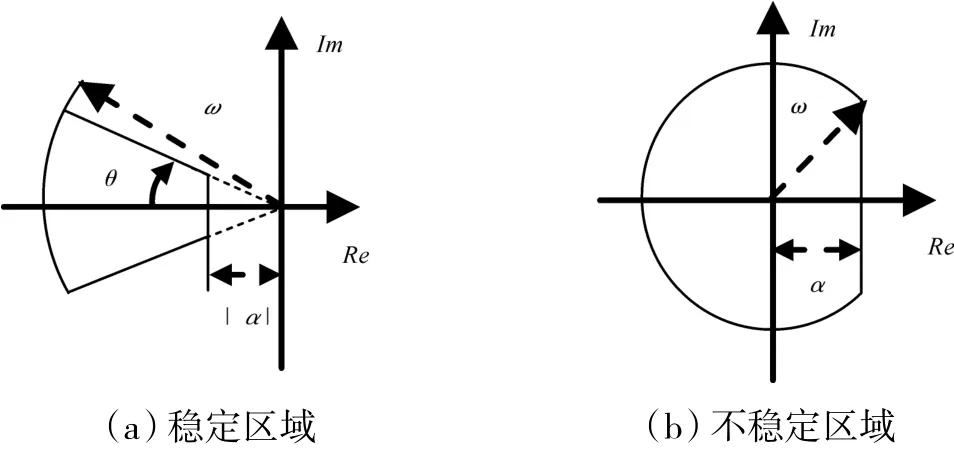
图6 不同类型的区域
如图6(a)所示的稳定集合区域Ω的定义为
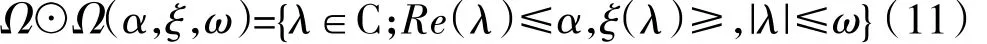
式中:ξ(λ)为 λ 的阻尼比。
如图6(b)所示的不稳定集合区域Ψ的定义为
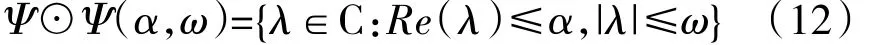
定义2:矩阵M为Hurwitz稳定矩阵,其所有特征值为 Λ={λ1,λ2,…,λn},区域 ΩΛ⊙Ω(αΛ,ξΛ,ωΛ),其中αΛ=max{Re(λi)};ξΛ=min{ξ(λi)};ωΛ=max{|λi|}。区域Ωt=Ω(αt,ξt,ωt)为目标区域,则定义区域Ωu=Ω(αu,ξu,ωu),其中,αu=max{αt,αΛ};ξu=min{ξt,ξΛ};ωu=max{ωt,ωΛ}[15]。
定义3:矩阵M为Hurwitz稳定矩阵,其所有特征值为 Λ={λ1,λ2,…,λn},区域 Ψ⊙Ψ(αΛ,ωΛ),其中αΛ=max{Re(λi)};ωΛ=max{|λi|}。区域Ωt=Ω(αt,ξt,ωt)为目标区域,则定义区域 Ψu=Ψ(αu,ωu),其中,αu=αΛ;ωu=max{ωt,ωΛ}[15]。
3.2 目标区域增益预置算法
系统的动态性能主要取决于系统极点的位置,其不仅决定系统的稳定性,还决定系统的动态性能。因此,若能通过控制器设计将闭环系统的极点配置到目标位置,则相当于使系统具有期望的性能。基于保护映射理论的目标区域增益预置算法[16]流程如图7所示。运用该算法可根据任意选择的初始控制器增益,计算得到控制器增益向量K,使控制系统的闭环极点位于目标区域Ωt=Ω(αt,ξt,ωt)内,从而获得期望的性能。
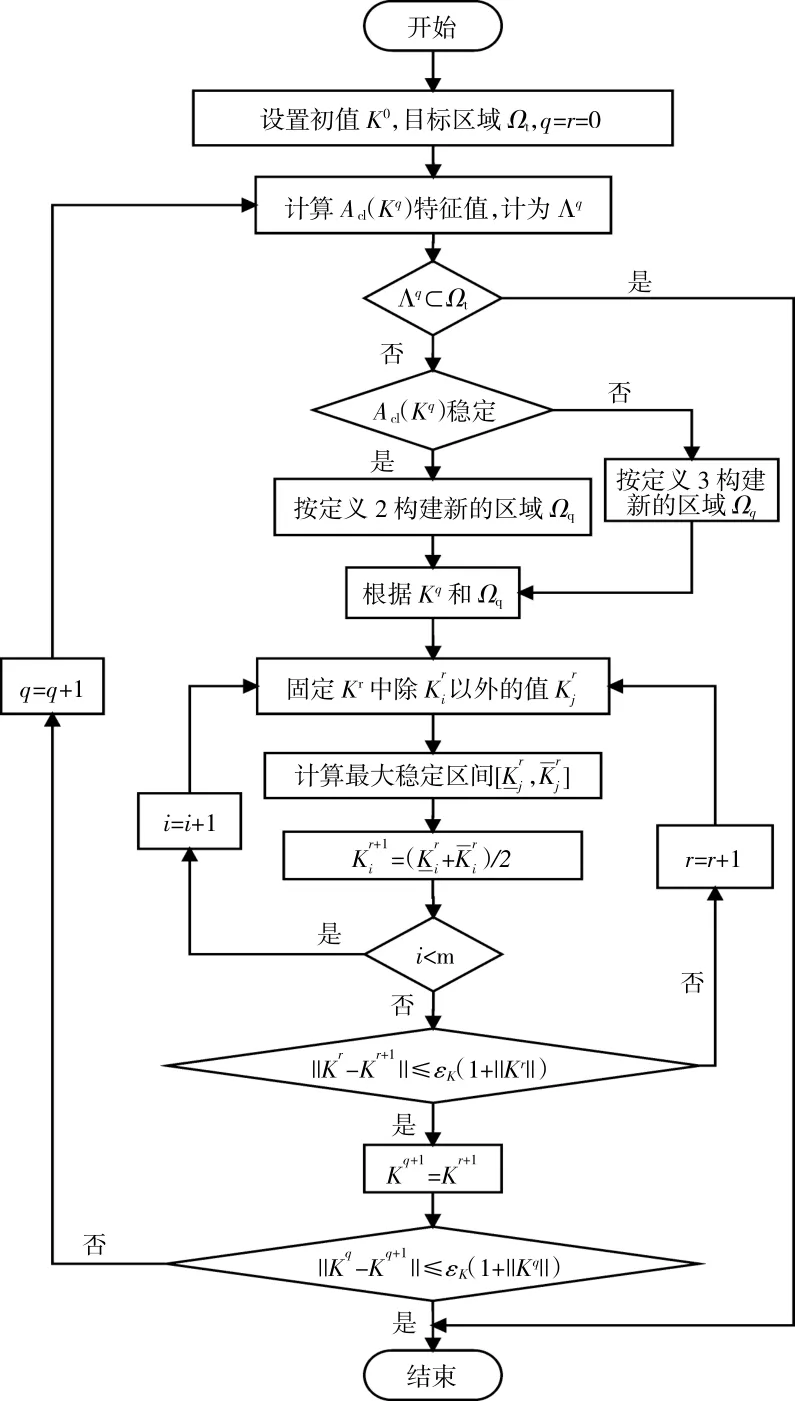
图7 增益预置算法流程
算法的具体步骤为:
(1)设K=[Kj(]j=1,…,m)表示控制系统的增益向量,K0=[]表示初始增益向量,Ωt=Ω(αt,ξt,ω)t表示目标区域,q=r=0,此时 Kq=Kr=K0;
(2)计算闭环系统状态矩阵A(clKq)的特征值Λq={λ1,λ2,…},若 Λq⊂Ωt则跳出循环;
(3)根据A (clKq)的稳定性来构建新的区域:若稳定,则采用第 3.1 节中的定义 2 构建 Ωq=Ωu=Ω(αq,ξq,ωq);若A(clKq)不稳定,则采用第3.1节中的定义3构建 Ωq=Ψu=Ψ(αq,ωq);
(4)根据构建的新区域Ωq和Kq,进行如下循环迭代过程:
当||Kr-Kr+1||≤ε(K1+||Kr||)(εK为一较小的正数)时,则跳出循环,令Kq+1=Kr+1;否则,r=r+1,继续求解;
(5)当 ||Kq-Kq+1||≤ε(K1+||Kq||)时,循环结束,否则,q=q+1,返回到(2)继续运行。
3.3 单参数模型控制过程
设计满足控制性能要求并与调度参数ρ∈[ρmin,ρmax]相关的全局控制器是LPV模型控制器设计的关键。基于保护映射理论的单参数LPV模型的全局控制器设计流程[17]如图8所示。
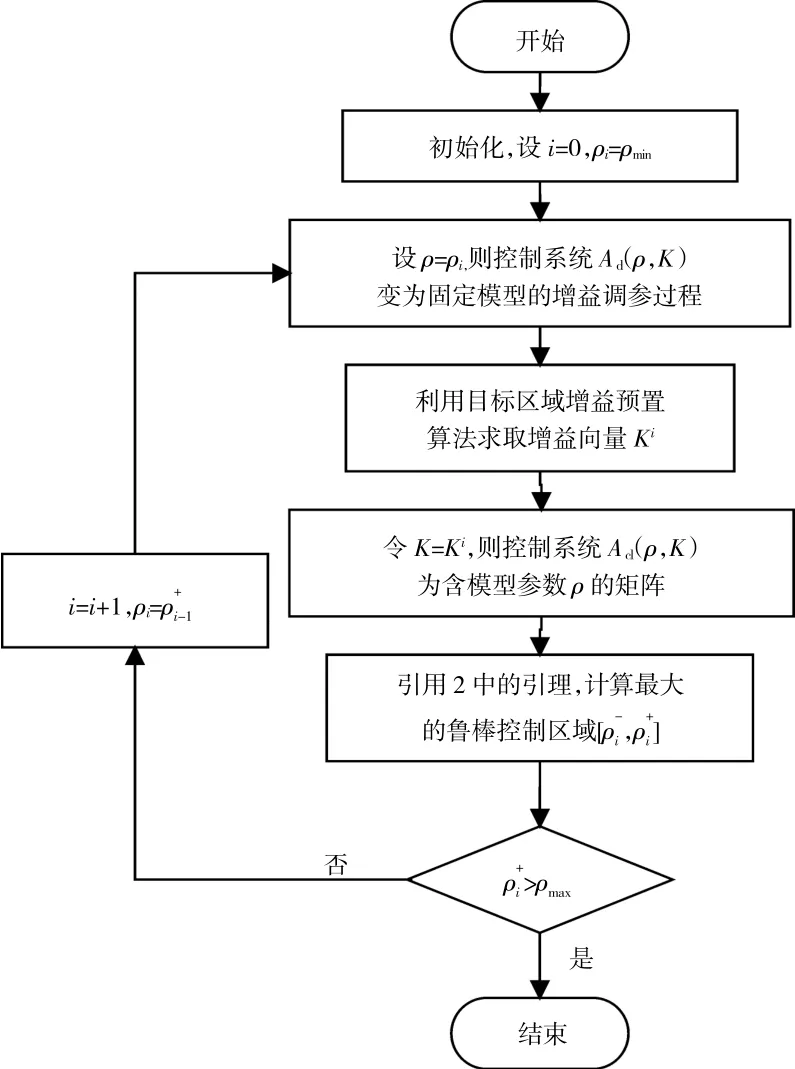
图8 单参数模型控制流程
算法的具体步骤为:
(1)设Ac(lρ,K)为闭环系统状态矩阵,K=[Kj(]j=1,…,m)为控制系统增益向量。设 ρ=ρ0=ρmin,则控制对象变为固定参数的模型;
(2)利用第3.2节中的算法求得满足控制要求的增益向量Ki;
(3)令K=Ki,此时A (clρ,K)中的变量仅为调度参数ρ,根据引理,可计算得此时Ki对应的满足控制要求的最大调度参数的范围为
4 控制器设计与仿真
4.1 控制器设计过程
本文选择PI控制器结构,因为其能使系统性能满足零稳态误差的要求并具有良好的动态响应。闭环系统的结构如图9所示。
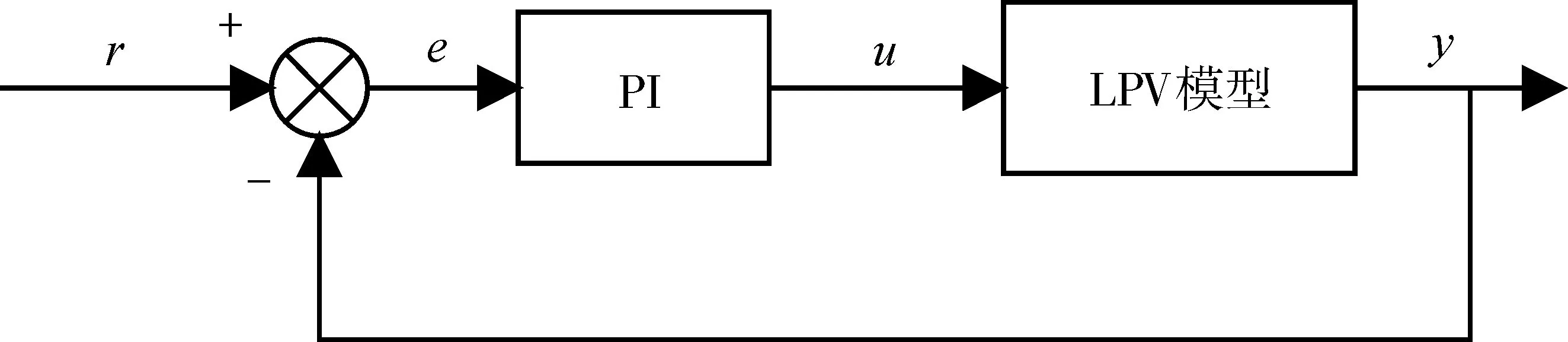
图9 控制器结构
PI控制器的传递函数为

本文运用上述基于保护映射理论的算法进行控制器K(s)设计,使LPV系统在整个调度参数的变化范围内达到控制要求。
在航空发动机控制系统设计过程中,最重要的是所设计的控制系统应满足性能指标要求。本文的控制器设计指标考虑衰减系数α、阻尼比ξ和自然频率ω,该设计指标可对闭环系统的稳态和动态性能进行表征。为保证系统具有良好的性能,本文根据航空发动机控制的目标要求,确定3个设计指标的取值分别为 α≤-1.7,ω≤8,ξ≥0.85,通过式(11)构建目标区域。根据保护映射性质,目标区域保护映射为
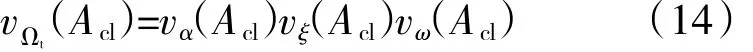
对已建立的H=0 km,Ma=0点LPV模型进行控制器设计,首先,令=0,任意选取PI控制器的初始值为Kp=Ki=1,通过第3.2节的算法可以得到控制器参数Kp=6.9735,Ki=15.5318,该控制器参数可将闭环系统的极点限制在目标区域内,从而获得期望的性能。其次,通过第2章中的引理可以得到该控制器参数能够使系统关于 Ωt稳定的最大区间为[-0.0154,0.1308],在该调度参数变化区间内,闭环系统的极点均位于目标区域中。再次,取上限值=0.1308,根据第3.3节中方法获得新的PI控制器参数值,以及与之对应的稳定区间,按照这样的流程进行循环计算,直到∈[0,1]中所有的均有与之对应的控制器。控制器设计的迭代运算结果见表1。从表中可见,每次计算出的稳定区间存在一定的重合,为了保证系统在整个调度参数变化范围内均相对于稳定区域稳定和控制器的控制效率,本文选择在重合区间的中点进行控制器的切换,切换过程如图10所示。
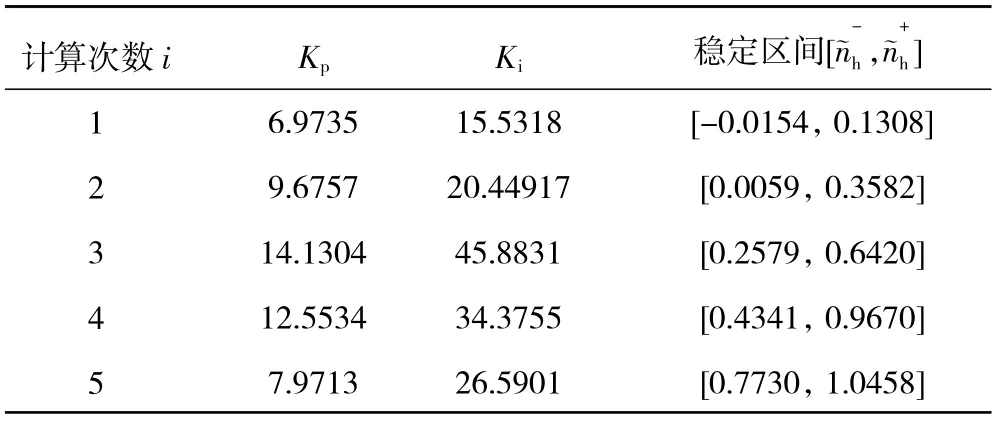
表1 控制器设计结果
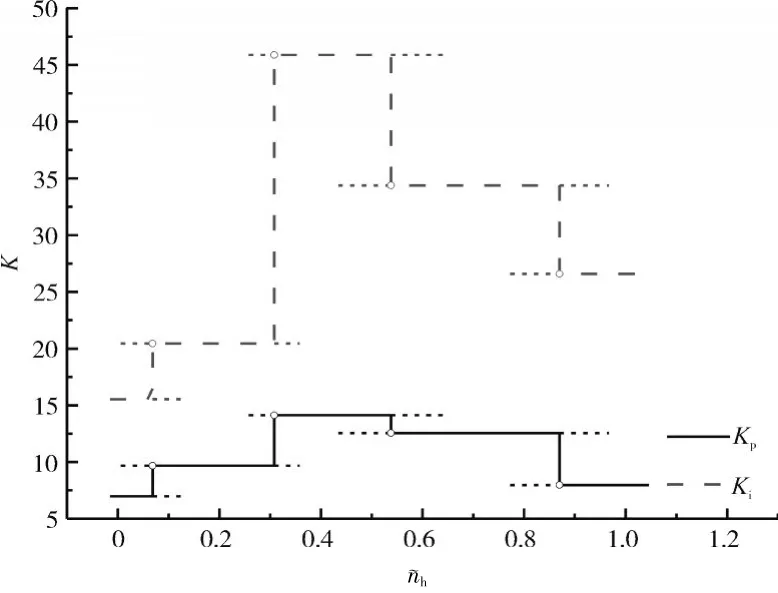
图10 控制器参数K随n˜h的变化规律
根据所设计的控制器计算不同转速下的闭环系统极点,其分布如图11所示。从图中可见,闭环系统极点均位于目标区域内,达到了预期设计目标。
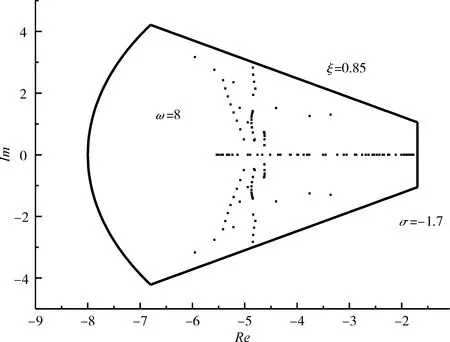
图11 闭环系统极点分布
4.2 仿真结果分析
为了避免航空发动机转速大范围变化时,系统产生较大的超调量,本文采用积分分离控制[18],即:在e>0.6(rt-r0)(e 为闭环系统偏差值;rt为闭环系统目标值;r0为闭环系统初始值)时忽略积分控制,仅采用比例控制。选取传统变增益PI控制器作为比较对象,其设计方法为:在相对高压转子转速变化区间内等间距的10个点处,通过遗传算法整定PI参数值[19],最后拟合出PI参数的多项式。在H=0 km、Ma=0点的阶跃仿真结果如图12、13所示。在H=3.5 km、Ma=0.5点采用相同的方法设计控制器并进行阶跃仿真,其仿真结果如图14、15所示。
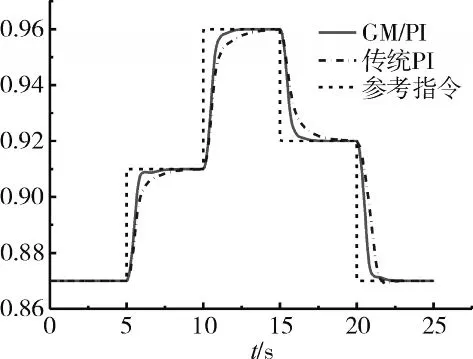
图12 在H=0 km、Ma=0时高压转速仿真结果
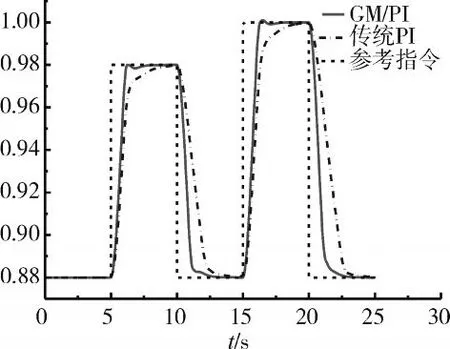
图13 在H=0 km、Ma=0时高压转速大范围变化仿真结果
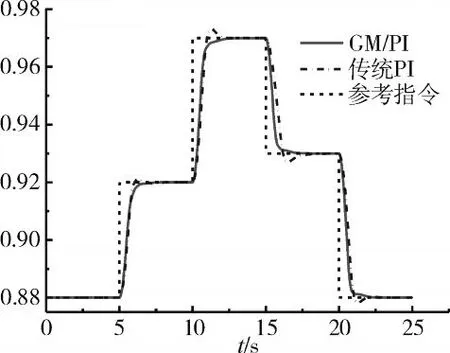
图14 在H=3.5 km、Ma=0.5时高压转速仿真结果
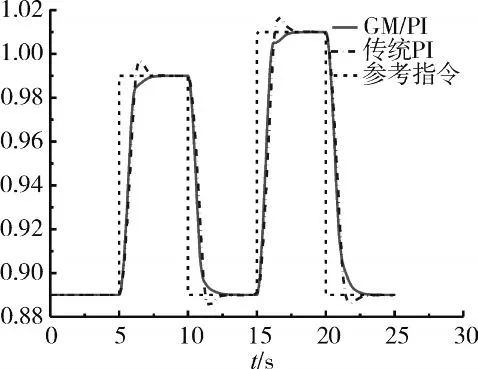
图15 在H=3.5 km、Ma=0.5时高压转速大范围变化仿真结果
从图12~15中可见,在基于保护映射理论设计的PI控制器控制下,系统响应曲线的调节时间小于2 s,超调量小于0.8%,稳态误差为0。在传统变增益控制方法设计的PI控制器控制下,系统响应曲线的调节时间和超调量均较差,其调节时间小于3 s,超调量高达7%。由仿真分析可知,基于保护映射理论设计的PI控制器的控制效果比传统设计方法设计的PI控制器的控制效果具有更好的动态响应,在超调量和调节时间等性能上均有明显改善。
5 结论
(1)本文将基于保护映射理论的控制方法用于航空发动机控制系统设计中,在航空发动机非线性模型上的仿真结果表明,系统动态响应的调节时间小于2 s,超调量小于0.8%,稳态误差为0,具有良好的控制效果;
(2)本文将保护映射理论及其相关算法进行了详细说明,并将其运用在航空发动机控制系统设计中,采用PI控制器,具有工程易用性;
在后续研究中,可针对航空发动机更多变量,采用基于保护映射理论的方法进行控制器设计,进一步验证该方法在航空发动机控制中的有效性。同时,在控制器参数切换过程中,可采用加权法等进行重合区域控制器的切换,并进行控制系统性能分析。
