涡轴发动机部件特性修正及更新方法
2018-03-23周文祥潘慕绚黄开明
董 桢,周文祥,潘慕绚 ,黄开明
(1.南京航空航天大学江苏省航空动力系统重点实验室,南京210016;2.中国航发湖南动力机械研究所,湖南株洲412002)
0 引言
非线性部件级模型是航空发动机及其控制系统研制过程中不可或缺的仿真工具。模型的精度是建模过程中的1项关键技术指标,直接决定该模型的应用价值和适用范围。借助高精度的航空发动机性能仿真模型,通过计算机仿真及优化,可以大大缩短发动机数控系统的设计及测试周期,降低研发成本,同时还可避免不必要的试车风险[1-2]。
影响发动机部件级模型精度的1个重要因素是发动机部件特性。对发动机而言,零部件制造和装配过程必然存在着公差[3],并且在发动机寿命期内自然磨损、疲劳、腐蚀或积垢等原因也会引起相关部件的性能退化[4],从而导致设计出的发动机期望部件特性与实际装机的部件特性之间产生差异。若以期望部件特性为依据建立的数学模型表现出的整机性能,与实际发动机整机性能之间也必然存在一定差异。因此,模型修正技术对于提高发动机部件级模型精度非常重要。
国外学者早在20世纪90年代初就开始进行修正发动机部件特性和模型参数的方法研究。Stamatis A等[5-6]提出1种基于发动机实际测量数据的方法,将发动机模型的仿真输出和试车数据误差的加权平方和作为目标函数,采用非线性广义最小残差法求解共同工作方程;同样在试车数据的基础上,Joachim Kurzk[7-8]着眼于大气条件对发动机各截面总温、总压及流量等气路参数的影响,给出详细的修正方法。之后,优化算法逐渐引入部件特性修正中。Y.G.Li[9]采用牛顿-拉夫森算法求解不可测参数的修正因子,得到准确的不可测参数的真实值;Changduk Kong[10-12]从部件特性图着手,发现压气机流量可以近似表示为压比的3次多项式,效率可以近似表示为流量的3次多项式,其中多项式系数通过遗传算法优化得到。国内学者在发动机部件级模型修正方面也进行了深入研究。段守付等[13]在模型中引入加权函数和一系列修正因子,改变修正因子的取值使加权函数最小,实现对发动机部件特性和模型的最优修正;陈策等[14]建立BP神经网络对部件特性数据进行识别学习,实现特性数据的精确插值和对未知特性数据的推测;吴虎等[15]提出1种预测发动机部件特性的自适应模型方法,以通用特性为基础,运用单纯形优化方法预测出不同飞行条件下涡扇发动机的部件特性。上述修正方法在原理上具有相似性,但在求解非线性方程组或优化算法方面存在一定差异。
本文利用具有高效率和全局搜索能力的粒子群优化算法(Particle Swarm Optimization,PSO)来修正涡轴发动机的部件特性。在基本不改变部件级模型核心计算代码的情况下,使用PSO算法计算出部件特性图和其他参数的修正因子。
1 涡轴发动机建模
拟建模的涡轴发动机由进气道(包括粒子分离器)、组合压气机(包括轴流压气机和离心压气机)、燃烧室、燃气涡轮、动力涡轮和尾喷管组成,如图1所示,各截面定义见表1。
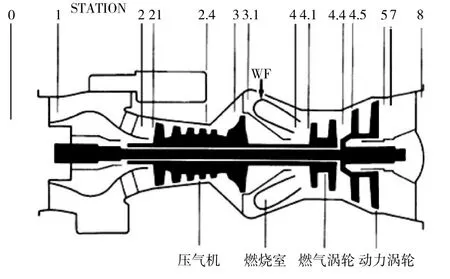
图1 涡轴发动机结构

表1 涡轴发动机各截面定义
涡轴发动机部件级模型的输入参数是大气压力、环境温度、高度、马赫数、燃气涡轮转速和动力涡轮转速。输出参数是燃油流量、各截面气动参数(总温、总压等)和性能参数(动力涡轮功率、耗油率等)。在建立所有部件的气动热力学模型后,选定4个仿真初猜值(压气机、燃气涡轮和动力涡轮压比及燃气涡轮转速),其对应的4个共同工作方程为
燃烧室出口和燃气涡轮进口燃气物理流量平衡方程

燃气涡轮出口和动力涡轮进口燃气物理流量平衡方程

动力涡轮出口和尾喷管进口燃气物理流量平衡方程

轴功率平衡方程
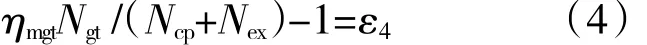
式中:Wg为燃气物理流量,下标数字为相应截面编号;Ngt为燃气涡轮输出功率;Ncp为组合压气机消耗功率;Nex为附件提取功率;ηmgt为燃气涡轮轴机械效率;εi(i=1,2,3,4)为平衡方程的残差。
利用牛顿-拉夫森法迭代求解共同工作方程组就可以得到稳态工作点。由上述4个共同工作方程结合各部件气动热力计算方程,构成发动机的稳态模型。在发动机稳态工作时,若共同工作方程的残差|εi|<ε0,i=1,2,3,4(其中 ε0为控制精度,本文取 10-3),则认为方程收敛,停止迭代。
2 粒子群优化算法
采用粒子群优化算法修正发动机部件级模型,其原理是利用PSO优化发动机模型的修正因子,使目标函数最小化或使适应度函数最大化。
2.1 待修正参数
对涡轴发动机部件级模型而言,待修正的参数包括旋转部件的部件特性(包括压比、换算质量流量和效率)、典型流道部件的总压恢复系数、压气机引、放气比例以及燃烧室效率。
修正设计点时,对上述参数都进行修正;修正非设计点时,本文只修正旋转部件的部件特性,其他待修正参数采用设计点的修正结果。
2.2 目标函数
选择燃油物理流量Wf、组合压气机增压比πcp、发动机进口空气物理流量Wa2、动力涡轮进口燃气总温T45以及输出功率Ne作为目标参数。
发动机测量参数的误差定义为

式中:ycal为计算参数;yact为基准参数。
目标函数定义为

式中:ai为各目标参数的权重系数,本文在优化过程中暂取1。
2.3 粒子群算法优化原理
粒子群算法是模拟鸟群觅食的过程[16-17]。每个优化问题的解都是搜索空间的1只鸟,称为“粒子”。每个粒子具有由优化函数确定的适应度值。每个粒子也具有1个速度,决定搜索的方向和距离。所有粒子追随当前最优粒子在解空间中搜索。
假设D维空间中的粒子群中的第i个粒子的位置表示为
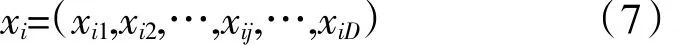
速度表示为
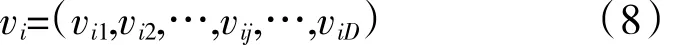
当前粒子群中的最优个体粒子表示为
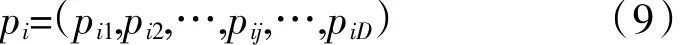
历代全局最优个体粒子表示为
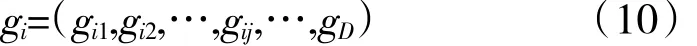
粒子群中的所有粒子根据式(11)和(12)更新速度和位置
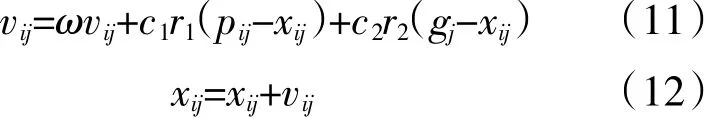
式中:r1和r2取(0,1)中的随机数;c1和c2为学习因子,通常取2;ω为惯性权重,取较大的值意味着粒子群具有较强的全局搜索能力,取较小的值意味着粒子群局部搜索能力达到最优。
所有粒子的速度和位置具有上下限,由实际问题决定。由式(11)和(12)组成的粒子群算法称为基本粒子群算法。
在此基础上,如果惯性权重的值根据迭代次数而减少,则算法被称为惯性权重线性递减粒子群算法[18]。一般来说,ω的初始值设为0.9,然后根据迭代次数将其线性减小到0.4。粒子群优化算法的惯性权重线性递减是粒子群算法中比较常见的算法模型。本文采用惯性权重线性递减粒子群优化算法优化涡轴发动机部件特性。
惯性权重定义为
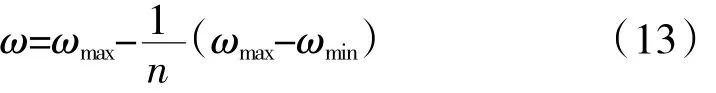
式中:i为当前迭代次数;n为总迭代次数。
本文粒子群总优化代数设置为300,所有待修正因子优化范围统一设置为[0.98,1.02]。适应度在初始100代以内急剧增加,然后减慢,在150代左右达到最大,如图2所示。
部件特性修正流程如图3所示。
需要特别说明的是,粒子群优化迭代过程中更新的是部件特性图,而不是部件流量或效率特性的修正因子,这样做的好处是一旦优化结束,可以直接输出修正后的部件特性图和其他有关模型参数,如总压损失、引放气比例等。
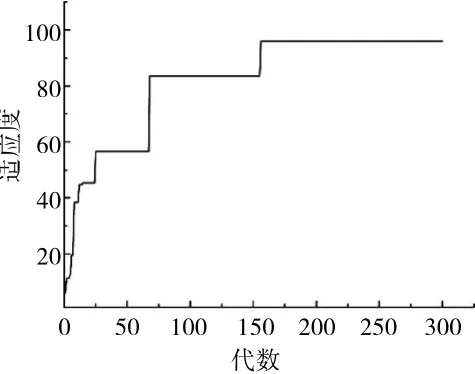
图2 粒子群适应度变化
3 部件特性图修正方法
压气机流量-压比特性如图4所示。图中描绘出待修正的一些稳态工作点,A为设计点,B、C、D为非设计点。对于设计点A,部件特性图将根据模型计算的结果与发动机设计点参数进行整体缩放。非设计点则是根据相对换算转速从高到低的顺序依次进行修正。例如,当修正工作点B时,保持L1不变并缩放L2,L4,…,Ln,以免影响设计点A的仿真精度。然后固定L1和L2,继续修正L4及更低的等换算转速线来修正工作点C。
上述修正方法假定在压气机2条等换算转速线之间只存在1个待修正工作点,这一假设条件在模型修正过程中有时是不满足的。图4显示在压气机L2和L42条等换算转速线之间存在C和D 2个工作点,针对这种情况,可以先选择距离设计点A较远的工作点D作为待修正点,对L4及其以下的等换算转速线进行整体修正,然后用工作点C来检验修正好的部件特性是否达到仿真精度要求。如若不满足要求,可以在点C和点D之间补充1条等换算转速线L3。这时问题转化成2条等换算转速线之间只有1个待修正点的情况,可根据前述方法对补作的特性线L3及其以下特性线进行修正,修正完毕后,继续根据点D的仿真结果修正L4及其以下转速特性线,如图5所示。

图4 压气机流量-压比特性
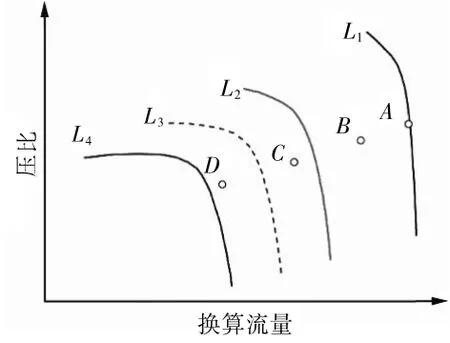
图5 补作等换算转速线后压气机流量-压比特性
为了验证提出的部件特性修正方案是否可行,本文从发动机性能分析软件GasTurb提取涡轴发动机通用部件特性图,以GasTurb软件计算结果作为模型修正基准值。在地面标况下(ISA H=0 km,Ma=0)选取燃气发生器转子相对物理转速分别为1、0.975、0.941、0.907的 4个工作点 A、B、C、D 来修正通用部件特性图。设计点A修正前、后各目标参数的稳态误差见表2。
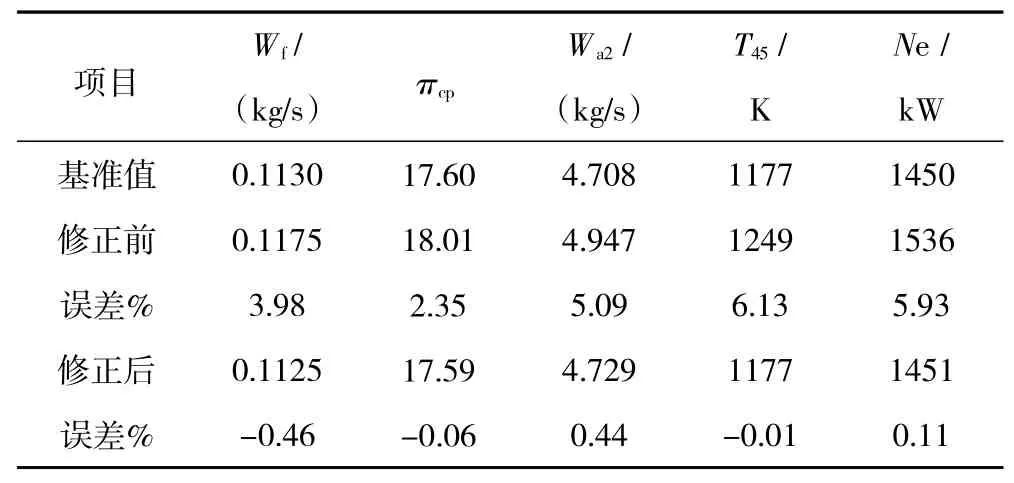
表2 设计点A修正前、后稳态误差对比(ISA H=0 km,Ma=0,n g=100%,n p=100%)
由表中可知,修正设计点A后,模型精度大大提高,设计点处模型平均稳态仿真误差由4.7%下降至0.2%。设计点A修正前、后压气机流量特性变化如图6所示。
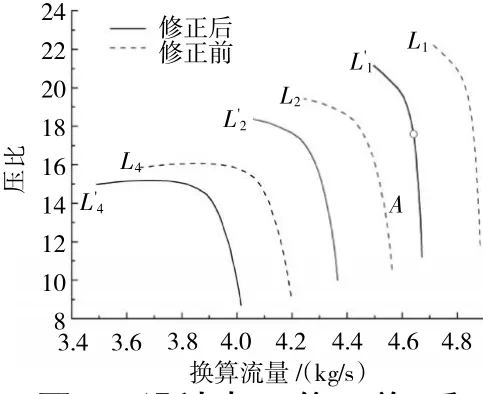
图6 设计点A修正前、后压气机流量特性对比
接着修正稳态工作点B。稳态工作点B修正前、后各目标参数的稳态误差见表3。
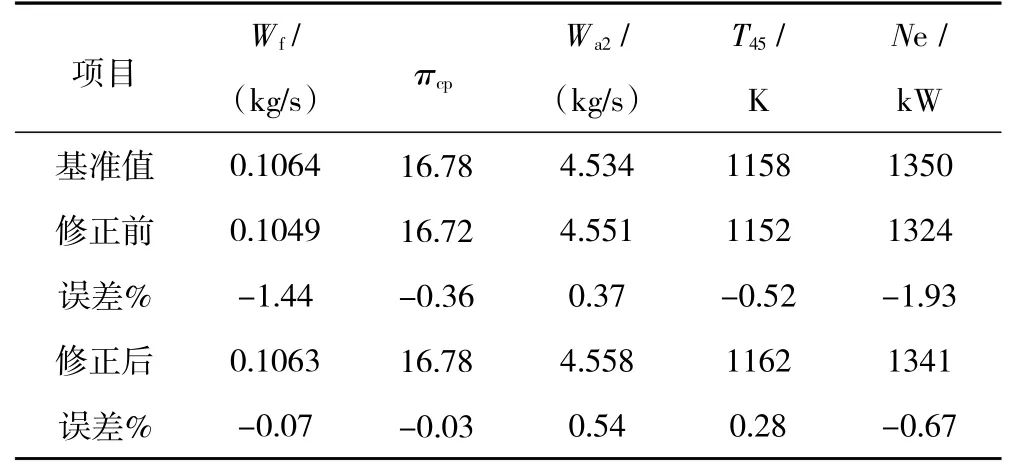
表3 稳态工作点B修正前、后稳态误差对比(ISA H=0 km,Ma=0,n g=97.5%,n p=100%)
稳态工作点B修正前、后压气机流量特性变化如图7所示。
由于稳态工作点C、D同时在2条等换算转速线之间,先修正稳态工作点D。稳态工作点D修正前、后稳态误差见表4。
修正后 A、B、D 3 个稳态工作点目标参数相对误差都在1%以内,满足精度要求。然后检验修正后的部件特性是否能够使稳态工作点C也满足指标要求。修正后稳态工作点C稳态误差见表5。
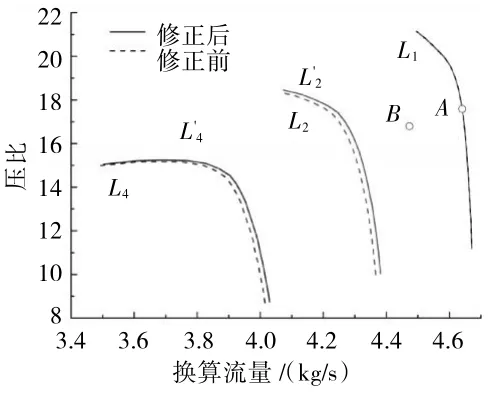
图7 稳态工作点B修正前、后压气机流量特性对比
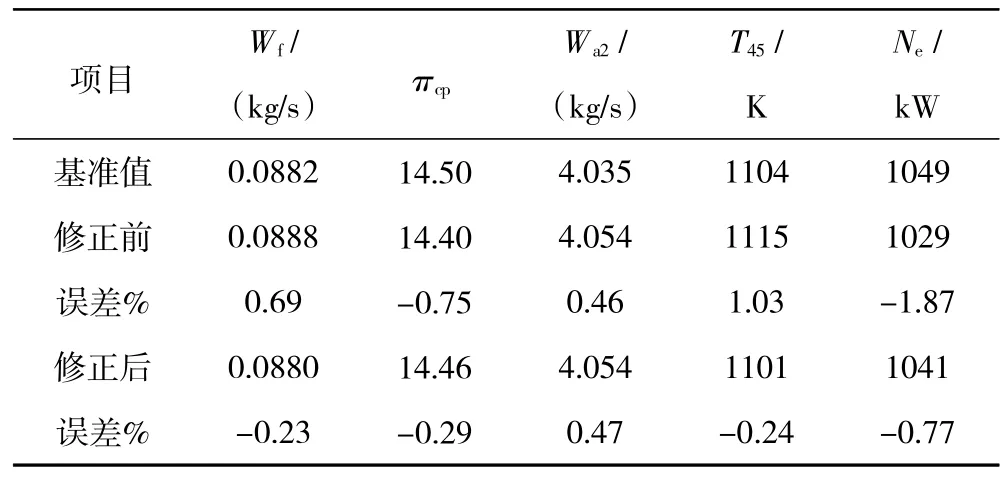
表4 稳态工作点D修正前、后稳态误差对比(ISA H=0 km,Ma=0,n g=90.7%,n p=100%)
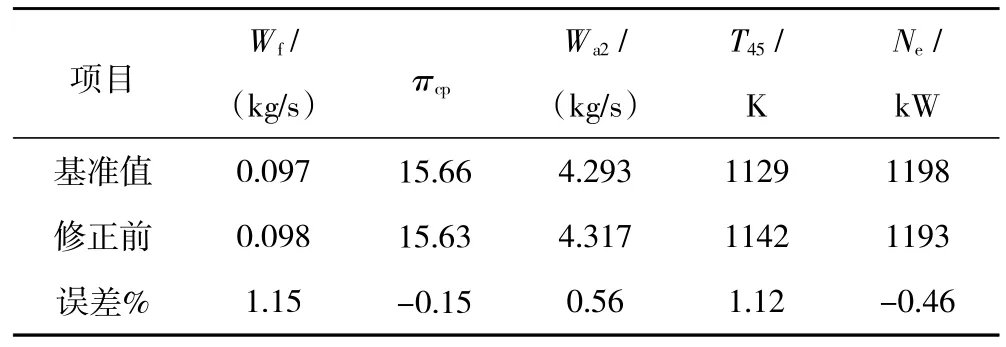
表5 修正后稳态工作点C稳态误差(ISA H=0 km,Ma=0,n g=94.1%,n p=100%)
从表中可见,Wf和T45的相对误差仍高于1%。因为这2个参数是反映涡轴发动机经济性及整机性能指标非常重要的参数,很有必要进一步提升其仿真精度,所以此处考虑在点C、D之间补作1条等换算转速线。补作的等换算转速线需要根据实际情况来确定,这里取相邻等换算转速的中值。
补作等换算转速线后稳态工作点C、D修正前、后稳态误差见表6、7。修正前、后压气机流量特性对比如图8、9所示,其中,L3为补作的等换算转速线。
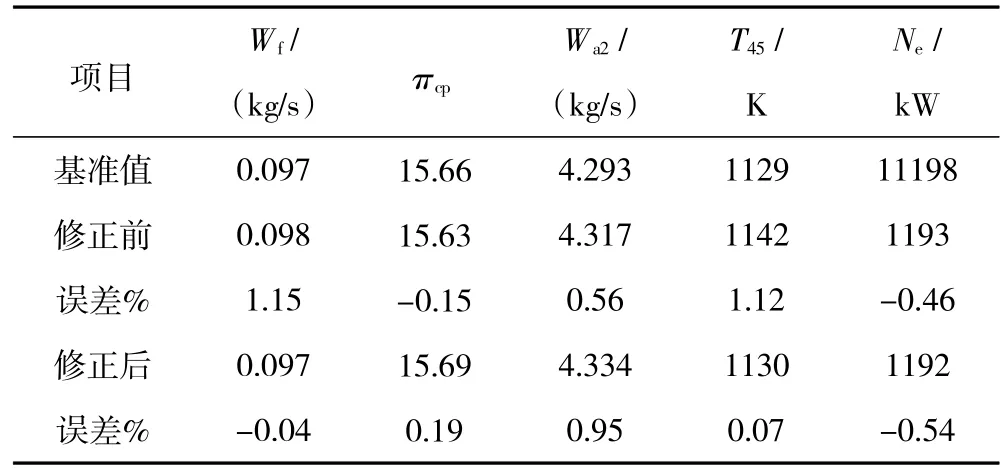
表6 补作等换算转速线后工作点C修正前、后误差对比(ISA H=0 km,Ma=0,n g=94.1%,n p=100%)
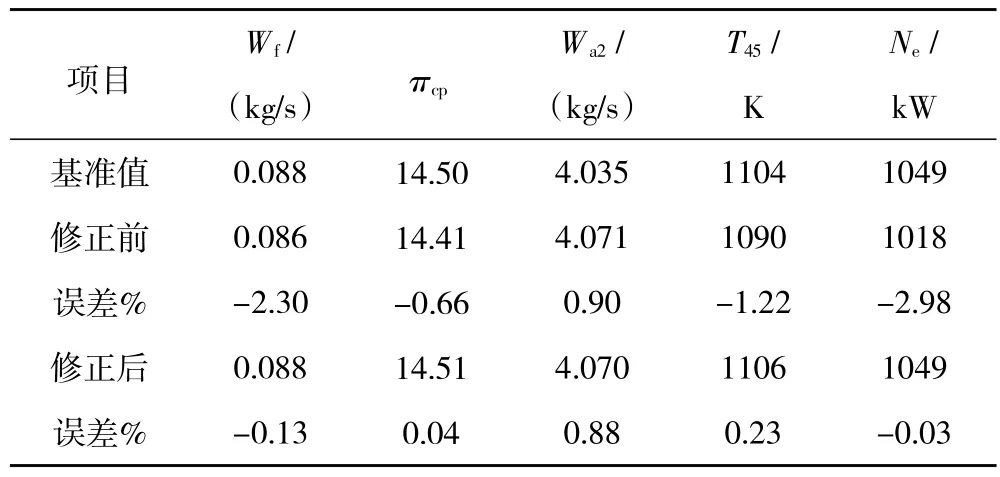
表7 补作等换算转速线后工作点D修正前、后误差对比(ISA H=0 km,Ma=0,n g=90.7%,n p=100%)
以上仿真结果表明,修正后点A、B、C、D目标参数稳态仿真误差均在1%以内,满足精度要求并且结果与预期相同。
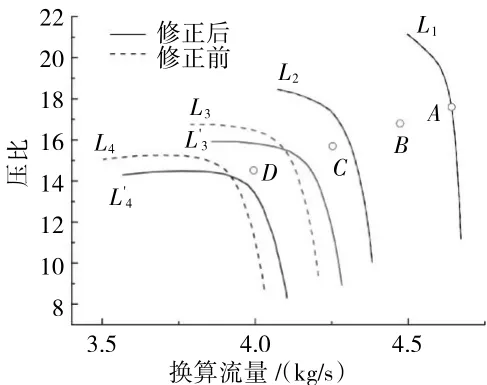
图8 稳态工作点C修正前、后压气机流量特性对比
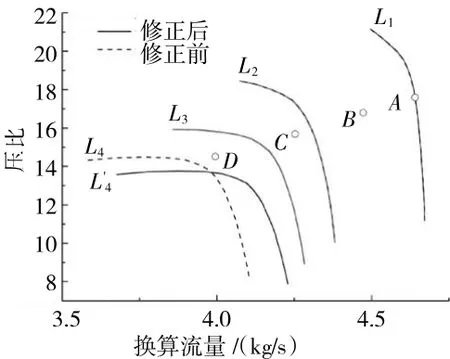
图9 稳态工作点D修正前、后压气机流量特性对比
压气机效率特性的修正与流量特性的修正方法一致,修正前、后压气机效率特性对比如图10所示。
修正涡轮部件特性时,2条等换算转速线之间存在B、C、D 3个稳态工作点。采用与压气机部件特性相同的修正方法,由于等换算转速线分布比较密集,修正稳态工作点D之后的特性能够使这3个稳态工作点同时满足精度要求。修正前、后涡轮流量特性对比如图11所示,涡轮效率特性对比如图12所示。
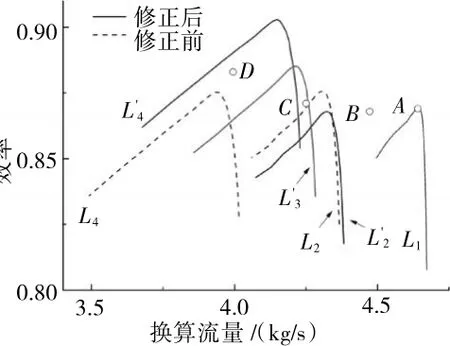
图10 修正前、后压气机效率特性对比
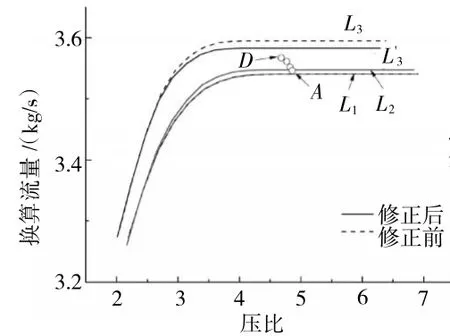
图11 修正前、后燃气涡轮流量特性对比
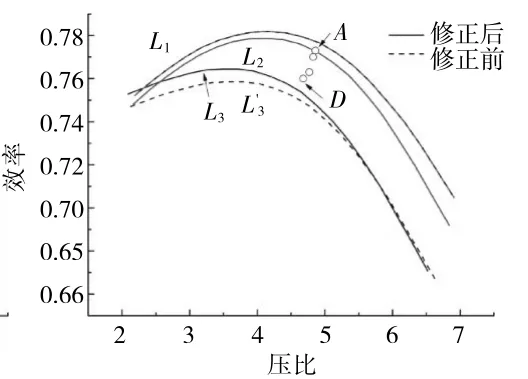
图12 修正前、后燃气涡轮效率特性对比
4 结论
本文提出基于粒子群优化算法(PSO)修正涡轴发动机部件特性的方法,通过模型计算结果与Gas-Turb仿真结果的对比,得到以下结论:
(1)用粒子群算法优化并更新已有的部件特性图可以有效减少部件级模型的稳态仿真误差。
(2)在模型修正过程中,不更新特性图只更新修正因子的方法对修正因子缺乏约束,求解出的数学解可能存在对应的发动机旋转部件效率大于1的情况,这与实际情况不相符。而本文提出的方法在每次优化修正结束后直接输出更新的部件特性图,可以直观地查看更新后的部件特性,有效避免了这一问题。
本文所提出的部件特性修正方法还有不足之处,例如在修正发动机非设计点的过程中,只是对发动机部件特性中的等换算转速线进行平移或者缩放处理,并没有改变其形状或趋势,有待引入更多的高空稳态工作点,进一步开展改变等换算转速线局部形状或趋势的修正方法研究。
