大口径红外光学系统方案设计

罗 秦，钮新华，张冬冬

(1. 中国科学院大学，北京 100049; 2. 中国科学院红外探测与成像技术重点实验室,上海 200083)

0 引言

空间遥感能够在距离地面200 km以上的轨道对地面目标或空间目标进行成像。先进的空间遥感技术能够准确预报森林火灾、测绘地图、估计农作物的产量、测定大气与海洋污染等。无论是军事还是民用领域都对光学系统的分辨率提出了越来越高的要求[1]。

光学系统分辨率的提高和光学系统的口径有直接的关系，口径越大光学系统分辨率越高。国外已发射的大口径高分辨率的相机有2001年发射的Quickbird2，口径为0.6 m，全波段星下分辨率为0.61 m；2008年发射的Geoeye-1，口径为1.1 m，全波段星下分辨率为0.41 m；美国的详查相机Keyhole12地面分辨率达到0.1 m，口径将近3 m。我国的米级高分辨率空间光学遥感器已有应用先例，如2014年发射的高分二号分辨率达到0.8 m，2015年发射的商业遥感卫星吉林一号分辨率达到0.72 m，但与国外的分辨率水平还有一定的距离，而且当前的高分辨率成像基本都是工作在可见近红外波段。为满足我国地热调查、城市热岛效应、火灾、智慧城市和军事侦察等应用需求，开展具有国际先进水平的红外高分辨率成像技术的研究具有重要的意义。

高分辨率红外成像需要光学系统具有大口径大相对孔径的特点，大口径光学系统一般采用全反射结构，常用的全反射系统有两反的卡塞格林系统、RC(Ritchey-Chrétien)系统等[2-3]；三反有同轴三反和离轴三反，大口径三反系统一般采用Korsch光学结构[4-8]；大口径光学系统F数越小，像差越难矫正，通过增加反射镜的个数来增加自由变量数以平衡像差，从而可以得到更加合理的系统，所以产生了四反、五反系统[9-13]。

本文针对某空间高分辨率红外相机成像要求，计算分析光学系统参数，利用光学设计软件ZEMAX设计了三种光学系统，通过对设计结果分析与对比，最终采用的同轴两反加离轴三反的组合式五反系统在奈奎斯特频率处的调制传递函数(MTF)设计值大于0.42，系统各项性能满足技术指标。

1 总体技术指标和光学系统参数

与光学成像要求相关的某空间相机总体技术指标如下：

1) 谱段范围，8～10 μm；

2) 最小分辨角，4 μrad；

3) 相机线视场角，±0.58°×0.03°；

4) MTF，>0.3(奈奎斯特频率处)；

5) 像元大小，28 μm×28 μm；

6) 光路尺寸，<4.0 m×3.5 m×3.5 m。

光学系统的基本参数有焦距、视场、工作波长和口径等，它们限制光学系统性能可达到的理论极限。角分辨率θ和系统最小口径D存在如下关系

(1)

角分辨率与像元尺寸a、焦距f′关系为

(2)

由最小分辨角θ=4 μrad，在工作波段内取λ=10 μm，可求得最小口径为D=3 050 mm。像元尺寸a=28 μm，可知系统焦距f′=7 000 mm。此时可知光学系统F数约为2.29。

奈奎斯特频率与像元尺寸有如下关系

(3)

将a=28 μm代入式(3)中可知，奈奎斯特频率为fNy=17.85 cy·mm-1。

2 光学系统方案分析

需要设计的空间相机口径达到3 050 mm，F数为2.29，工作在长波红外，采用反射式光学系统不仅需求的光学零件少，不存在色差，还可以进行轻量化设计，使得相机结构紧凑、体积小、质量轻，同时在抗热性能方面也有较强的优势。两反光学系统结构简单，装调容易，由于自由变量少，最多能消除两种初级像差，在大的相对孔径下无法获得满意的像质。通过增加反射镜的个数来增加自由变量数，大大增加消像差的可能性，从而产生三反系统，甚至四反、五反系统。三反系统有同轴三反和离轴三反，由于自由变量增加，三反系统可以同时矫正球差、彗差、像散和畸变四种初级像差。同轴三反按视场可分为对称视场系统和偏视场系统，离轴三反系统可以避免中心遮拦及MTF过高，因此在空间相机中得到广泛应用，但是结构松散会导致系统在垂直弧矢面方向的尺寸很大，这对于有限的星上空间资源是不利的，所以主光学系统需采用同轴方案。通过同轴两反主光学系统将口径缩小，再结合离轴三反后光学系统进行消像差，结合了同轴两反和离轴三反的优点，可以获得更好的成像质量。综合以上，本文提出了同轴三反、同轴偏视场三反系统方案和同轴两反加离轴三反的组合式五反系统方案。

在上述光学系统参数下，同轴系统的孔径又存在中心遮拦，有效通光孔径会减小，而光学MTF受限于光学系统F数、工作波长和有效通光口径，因此，中心遮拦总会引起同轴系统的MTF下降。图1为上述光学系统参数下10 μm波长时同轴三反系统遮拦比与奈奎斯特频率处衍射极限MTF的关系图，遮拦比定义为(Dob/D)2，Dob为遮拦口径，为了有较高的MTF，应对同轴系统的中心遮拦比进行控制。

图1 10 μm波长时遮拦比与衍射极限MTF的关系Fig.1 Relationship between obstructed ratio and MTF of diffraction limit with the wavelength of 10 μm

3 光学系统设计

根据系统参数及方案分析，本文提出了基于同轴光路的同轴三反、同轴偏视场三反和同轴两反加离轴三反的组合式五反系统的三种设计方案，下文将对设计方案进行全面的分析和比较。

3.1 三反光路初始结构

同轴三反系统初始结构计算理论已较成熟，初始结构如图2所示。M1、M2和M3分别代表三反系统中的主镜、次镜和三镜，其结构参量共有8个：三个反射面的半径(R1、R2和R3)，主镜到次镜的距离d1，次镜到三镜的距离d2，三个非球面的二次非球面系数(-e1)2、(-e2)2、(-e3)2。

引入新参数，次镜对主镜的遮拦系数为:α1=l2/(f1)′≈h2/h1；三镜对次镜的遮拦系数为:α2=l3/(l2)′≈h3/h2;次镜的放大率为:β1=(l2)′/l2=u2/(u2)′；三镜的放大率为:β2=(l3)′/l3=u3/(u3)′。将上述参数代入Seidel像差公式，可得初级像差系数S1，S2，S3，S4的表达式，令S1=S2=S3=S4=0，可以确定(-e1)2、(-e2)2、(-e3)2。

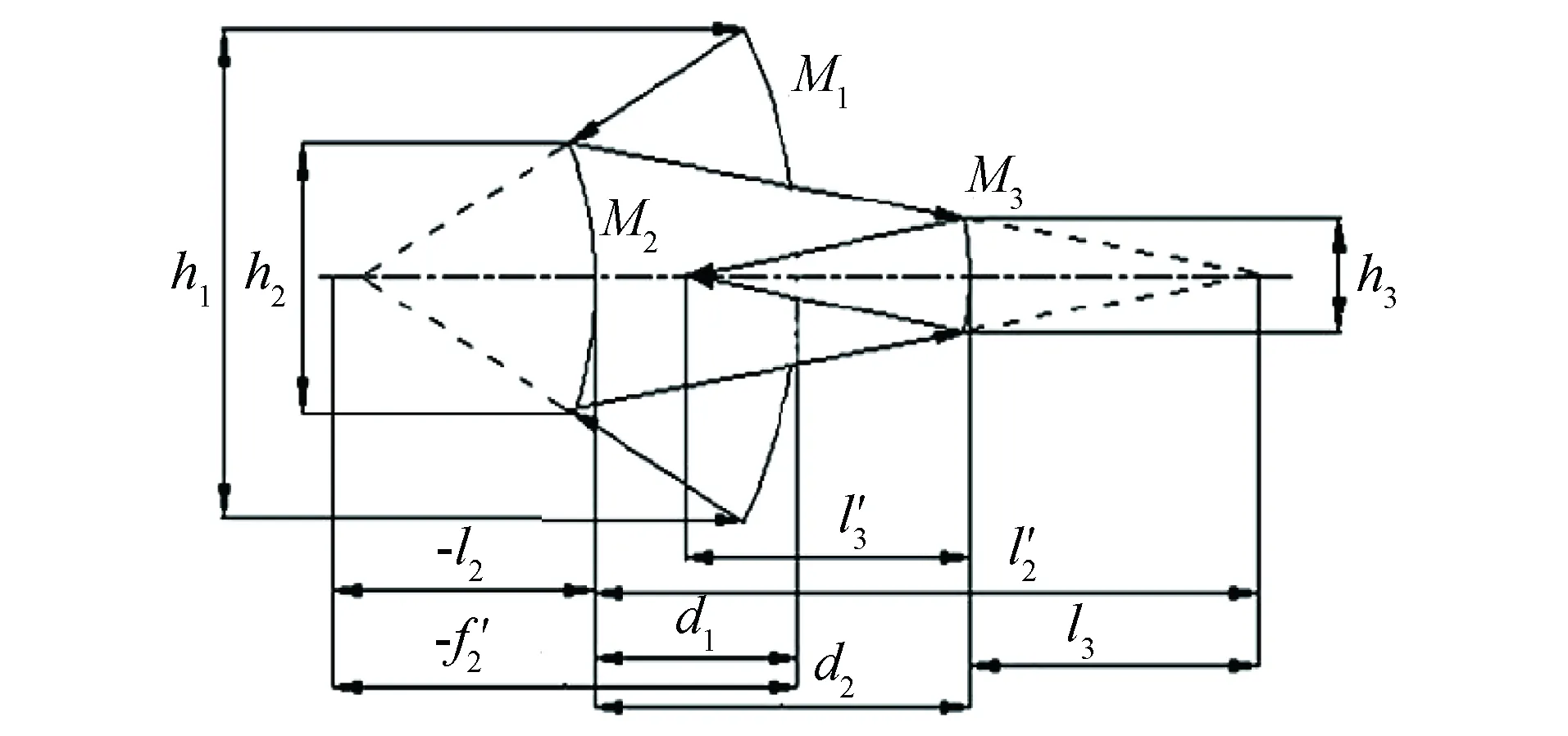
图2 同轴三反系统初始结构Fig.2 Initial structure of coaxial three-mirror system

剩余三个可变参量，如果再给定有关结构方面的三个条件，则整个系统初始结构就可以确定[14]。获得的一组初始结构数据如表1所示。

表1 同轴三反光学系统初始结构参数

3.1.1 同轴三反系统

将上文得到的初始结构参数输入到光学设计软件中，通过添加约束，在三镜后合适的距离处设置折镜，将像面转出光轴，经过优化后设计的同轴三反镜光学系统结构如图3(a)所示。X轴方向视场大小为±0.58°，Y轴方向视场大小为±0.015°，全视场奈奎斯特频率处MTF大于0.35，点列图和MTF如图3(b)和图3(c)所示。三面反射镜都是二次非球面，主镜为3 050 mm口径的椭球面；次镜为口径960 mm的凸双曲面镜；三镜为口径1 244 mm的凹椭球面镜。具体结构参数如表2中S1所示，光学系统总尺寸约为：3 000 mm×3 050 mm×3 050 mm。

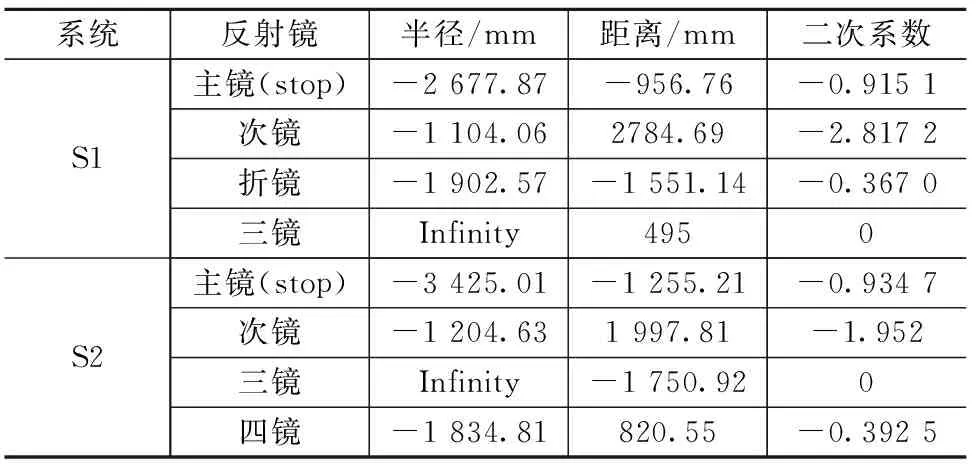
表2 同轴三反光学系统结构参数

图3 同轴三反光学系统Fig.3 Coaxial three-mirror optical system

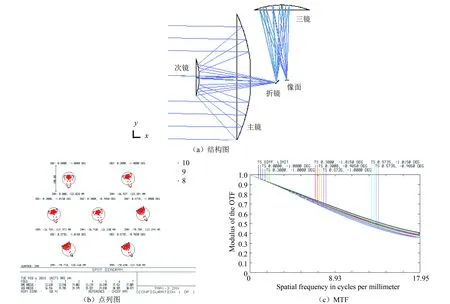
图4 同轴偏视场三反系统Fig.4 Coaxial eccentric-field three-mirror system

该系统的孔径光阑设置在主反射镜上，主镜与入瞳重合，系统为二次成像系统，折镜位于第一像面上，折镜中心挖孔通光同时作为视场光阑起到消除杂光的作用。这个系统三个反射镜都在一条轴上，装调较简单，结构紧凑，但主镜F数为0.43，且是一个接近抛物面的椭球面，单镜的加工和检验有难度。次镜是个大口径的凸非球面，其加工和检验同样有难度。

3.1.2 同轴偏视场三反系统

根据系统线视场工作的特点，为了加大主镜F数，避免折镜二次遮拦问题，在3.1.1节的结构基础上，将折镜设置在中间像面上，进行非过孔偏视场设计。通过添加约束条件进行优化，得到的同轴三反偏视场光学系统如图4(a)所示，X方向视场为±0.58°，Y向为偏视场为-1°±0.015°。全视场奈奎斯特频率处光学MTF大于0.35，点列图和MTF如图4(b)和(c)所示。主镜为3 050 mm孔径的高次椭球面；次镜为口径890 mm的凸二次双曲面；三镜为口径1 358 mm的凹高次椭球面。具体结构参数如表2中S2所示，光学系统总尺寸约为：2 500 mm×3 500 mm×3 050 mm。

该系统的孔径光阑设置在主反射镜上，主镜与入瞳重合，系统也为二次成像系统，折镜位于第一像面附近，在第一像面处设置视场光阑，可以有效地消除杂光。相对于上一个系统，通过折镜将光轴翻折90°，由于采用偏视场，就不用考虑二次遮拦的问题。主镜口径为3 050 mm，主镜和三镜Z轴方向间距不易拉开，给主镜支撑结构安装带来不便。F数为0.56。次镜是个大口径的凸非球面，其加工和检验同样有难度。

3.2 同轴两反加离轴三反的五反系统

上述三反系统主镜承担了较大的光焦度时，单镜F数很小。采用主光学系统加后置光学系统组合的方式，可以通过增加自由变量来减轻对主镜的要求。系统整体初始结构计算很复杂，可以通过主光学系统和后光学系统初步分配光焦度，即另同轴两反和离轴三反各占系统总光焦度的一半，分别计算同轴两反和离轴三反的初始结构参数。同轴两反系统初始结构计算较同轴三反简单，离轴三反初始结构是同轴三反经视场离轴或光阑离轴得到，这里不再赘述，具体计算可以参照文献[8]。最后再将两者合并一起输入到光学设计软件中逐步优化得到合适的结构。

复杂的组合式五反系统优化是关键，在优化中先将离轴三反结构参数定为变量，添加约束条件进行优化，到无法优化的程度将离轴三反结构设为不变量，再将同轴两反结构参数设为变量进行优化，最后将所有参数设为变量进行优化，一直反复以上过程直到得到满意的结果。最终，设计的五反系统如图5(a)所示，主光学系统为同轴两反，后光学系统为离轴三反，离轴三反光轴相对同轴两反光轴沿Y轴偏移-170 mm，X轴方向视场±0.58°，Y轴方向视场±0.015°，优化后光斑弥散斑都在艾里圆直径内，全视场内奈奎斯特频率处光学MTF大于0.42，如图5(b)和(c)所示。主镜为二次抛物面，次镜为口径600 mm的二次双曲面，三镜为高次双曲面，有效口径为480 mm×150 mm，离轴量为165 mm，四镜为凸高次扁球面，有效口径为160 mm×100 mm，五镜为凹高次椭球面，有效口径为320 mm×220 mm，离轴量为-130 mm。具体结构参数如表3所示。光学系统总尺寸约为：3 500 mm×3 050 mm×3 050 mm。

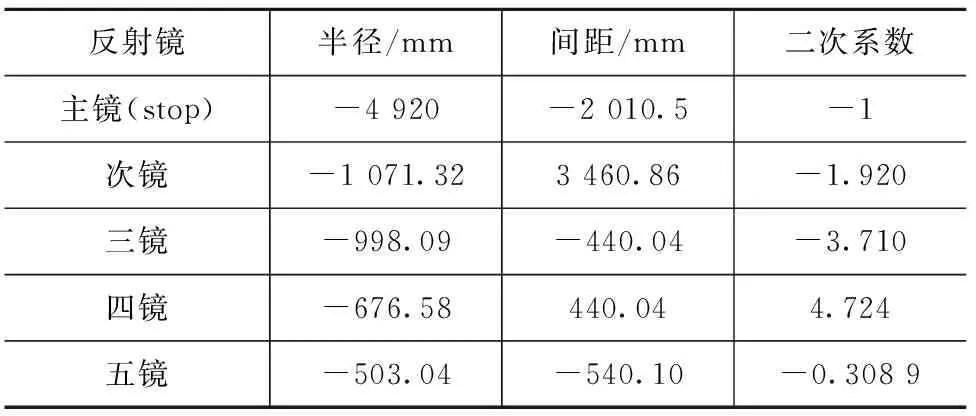
表3 五反光学系统结构参数

系统孔径光阑设置在主镜，在一次像面处设置视场光阑，可以用来消除杂光，主镜到三镜间距1 450 mm，方便安装主镜支撑结构。离轴三反结构紧凑，节省了占用空间。主镜被优化成抛物面，F数为0.82。

3.3 设计方案选定

虽然以上三种方案都可以满足设计指标，但都有各自的优缺点，如表4所示。同轴三反系统优点是反射镜少便于装调，但由于反射镜少自由变量少，方案1主镜F数很小，且是个很接近抛物面的椭球面，加工和检验都是难题，而且由于一次像面位于折镜中心孔处，开孔会导致三镜反射回的部分光线损失掉。方案2采用同轴偏视场，主镜是高次椭球面，加工和检验都较难，主镜与三镜Z轴方向间距较小，不便于安装主镜支撑结构。方案3增加了两个反射镜，自由变量增多，优化后MTF大于0.42，主镜优化成二次抛物面，次镜优化成二次双曲面，加工检验难度降低很多。从公差分析结果可知装调公差较严，随着离轴三反装调技术越来越成熟，可采用同轴两反加离轴三反的五反光学系统作为设计方案。

图5 同轴两反加离轴三反的五反系统Fig.5 Five-mirror system with coaxial two-mirror and off-axis three-mirror

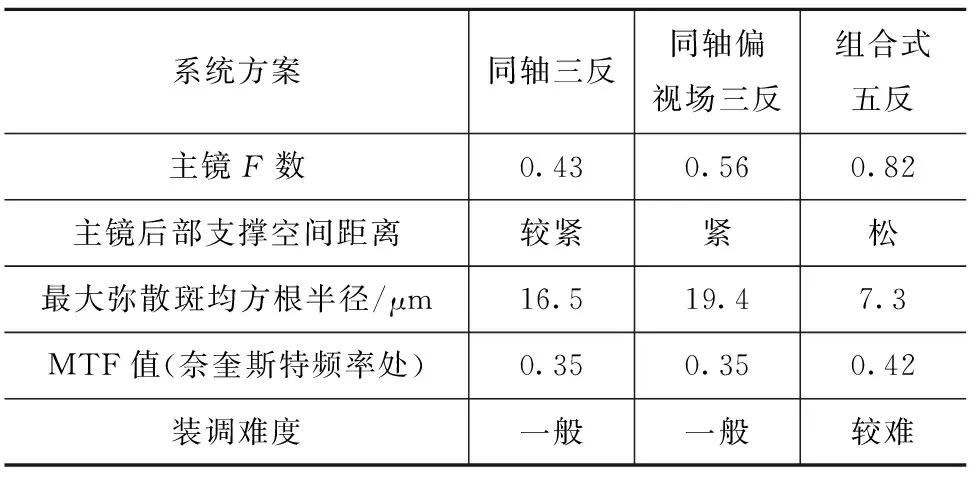
表4 三种方案对比

3.4 主镜结构

选定的方案主镜直径为3 050 mm，F数为0.82，口径太大，单镜整体加工较难，对于3 m级口径的非球面反射镜加工和检验都是很大的问题，詹姆斯韦伯空间望远镜(JWST)主镜口径达到6 m级别，主镜采用18块子镜拼接，减轻了设计加工难度[15]。采用类似的思想，将主镜分成由18块边长为750 mm的正六边形子镜进行拼接，拼接方案如图6(a)所示，由于拼接后有部分集光面积损失，系统的Huygens MTF有所降低，主镜为单镜时系统Huygens MTF如图6(b)所示，主镜为合成孔径且不考虑子镜拼接失调误差时系统MTF如图6(c)所示，全视场内Huygens MTF设计值大于0.4，满足成像要求。子镜的拼接失调误差有：子镜倾斜误差、piston误差、平移误差。子镜的失调会严重改变波前分布，影响系统成像。要保证成像质量，子镜失调产生的最大光程差要小于主镜面形精度的峰谷(PV)值，主镜面形精度PV值为波长级别，所以子镜拼接有严格的公差要求。

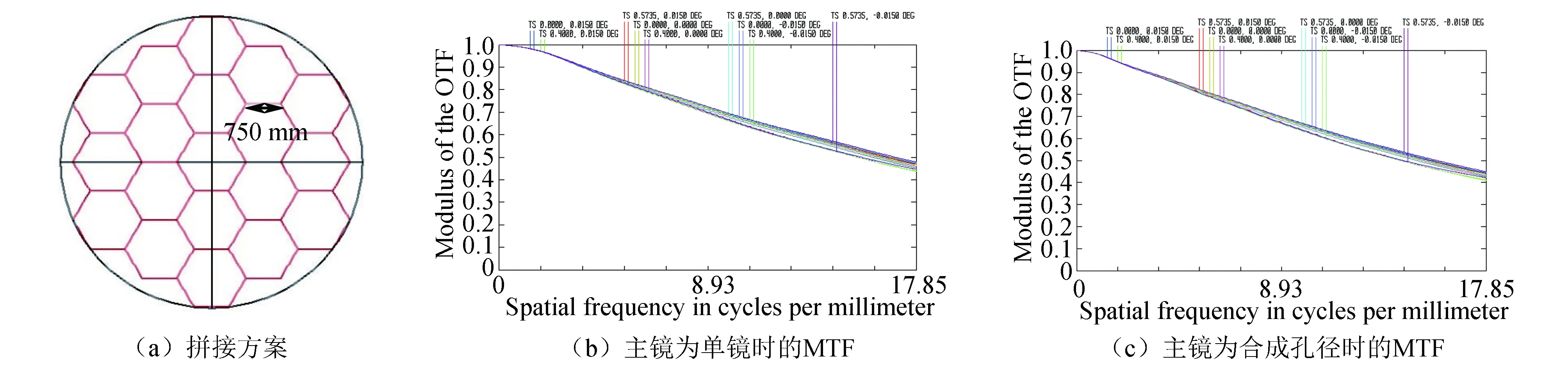
图6 主镜为合成孔径Fig.6 Synthetic aperture as primary mirror

4 结束语

针对角分辨率为4 μrad，工作波长为8～10 μm，探测器像元为28 μm的某空间相机，本文提出了三种设计方案，分别是传统的同轴三反系统和同轴偏视场三反系统，以及新的同轴两反加离轴三反的组合式五反系统。三个方案各有其优缺点，在综合考虑成像性能和光学加工、检测和系统装调等技术的基础上，由于组合式五反系统成像质量更高，主镜F数更大，所以选择组合式五反系统作为设计方案。该系统全视场、全波段在奈奎斯特频率处的MTF都优于0.42，主镜口径太大，单镜整体加工检验较难。本文采用合成孔径后降低了主镜的加工和检验难度，使全视场内MTF优于0.4,各项性能指标满足了设计要求。不足之处在于五反系统装调难度较大，后续工作还需要对系统装调和加工检验方案进行研究。

[1] 韩昌元. 高分辨力空间相机的光学系统研究[J]. 光学 精密工程, 2008, 16(11): 2164-2172.

[2] STAVROUNDIS O N. Two-mirror systems with spherical reflecting surfaces[J]. Journal of the Optical Society of America B, 1967, 57(6): 741-748.

[3] 潘君骅. 一个新的泛卡塞格林望远镜系统[J]. 光学精密工程, 2003, 11(5): 438-441.

[4] LAMPTON M, SHOLL M. Comparison of on-axis three-mirror-anastigmatic telescopes[J]. Proc SPIE, 2007, 6687: 66870S.

[5] JOHNSON R B. Wide field of view three-mirror telescopes having a common optical axis[J]. Optical Engineering, 1988, 27(12): 1046-1050.

[6] 李旭阳, 李英才, 马臻, 等. 高分辨率空间相机共轴三反光学系统实现形式研究[J]. 应用光学, 2009, 30(5): 717-723.

[7] 韦晓孝, 许峰, 余建军. 高分辨率空间同轴偏视场三反光学系统设计[J]. 中国激光, 2012, 39(4): 0416002.

[8] 李旭阳, 杨洪涛, 贺天兵, 等. 新型三反光学系统设计[J]. 光子学报, 2012, 41(1): 31-35.

[9] 梁士通, 杨建峰, 薛彬, 等. 四反射镜光学系统像差分析与设计[J]. 光学学报, 2010, 30(11): 3300-3305.

[10] SASIAN J M. Flat-field, anastigmatic, four-mirror optical system for large telescopes[J]. Optical Engineering, 1987, 26(12): 1197-1199.

[11] COOK L G. Compact four-mirror anastigmatic telescope: US6767103B2[P]. 2004-07-27.

[12] LI X L. An optical design of off-axis four-mirror-anastigmatic telescope for remote sensing[J]. Optical Society of Korea, 2012, 16(3): 243-246.

[13] JOHN F S. Optically fast, wide field-of-view, five-mirror anastigmatic (5MA) imagers for remote sensing applications[J]. Proc SPIE, 2011, 8158: 815804.

[14] 潘君骅. 光学非球面的设计、加工与检验[M]. 苏州: 苏州大学出版社, 2004: 131-134.

[15] LIGHTSEY P A, ATKINSON C B, CLAMPIN M C, et al. James Webb space telescope: Large deployable cryogenic telescope in space[J]. Optical Engineering, 2012, 51(1): 011003.