非典型几何问题的两种求解方法

李五明，刘桂仙

（河南理工大学 数学与信息科学学院，河南 焦作 454000）

引言

柱面方程的求解是高等院校数学类专业核心课程《解析几何》中一个很重要的内容。按照吕林根、许子道所编教材[1]，欲求一个柱面的方程，只需要知道准线的方程以及母线的方向数，根据“消参数法”，即可得到柱面的方程。圆柱面作为一种特殊的柱面，由于其特殊的性质，在求解其方程时，如果不知道其准线方程，可以不按照常上述规方法进行求解；同时也可以根据已知条件求出其准线方程，再按照“消参数法”求解。很多学生对教材[1]147页第3题圆柱面方程的求解非常困惑，主要是因为题设条件并没有给出圆柱面准线的方程，按照常规方法表面上看好像无法求解。文章针对这个非典型几何问题，同时考虑到圆柱面的特殊性质，给出其两种求解方法。

1 圆柱面方程的两种求解方法

原题如下：

求过三条平行直线 x=y=z，x+1=y=z-1与x-1=y+1=z-2的圆柱面的方程。

解：方法一（非常规方法）：因为圆柱面是三维空间中到轴线距离相等的点的集合，故可根据已知条件求出轴线的方程，进而求出圆柱面方程。设P（x，y，z）为轴上任意一点，则P到三条母线的距离相等，分别设为 d1，d2，d3，即有：

由点到直线的距离相等可得：

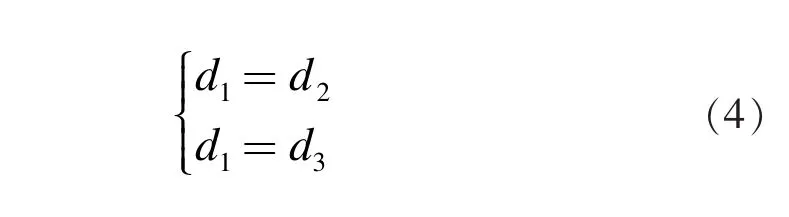
将式（1）（2）（3）代入式（4）化简后即为

即为圆柱面轴上的点所满足的方程（轴线方程），化为标准方程即为

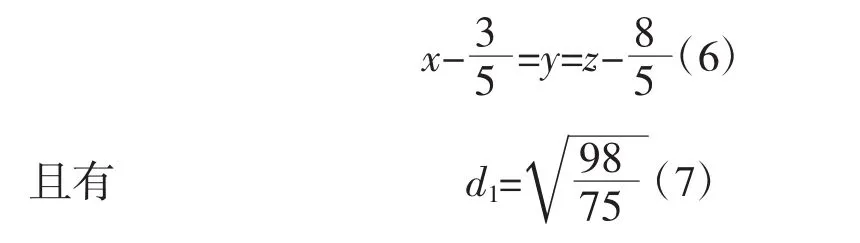
化简整理得

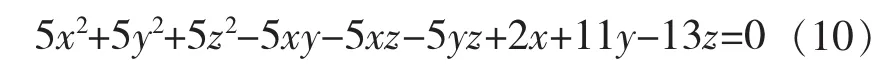
即为所求圆柱面的方程。

方法二（常规方法）：根据教材[1]，欲求柱面方程，需要知道其一个准线方程。圆柱面的准线有很多，但是在这里我们考虑求其中与母线垂直的一个准线方程，从几何上来说，该准线是一个圆，我们用一个球面和一个平面的交线来表示这个圆。已知圆柱面的一条母线为 x=y=z，其过原点（0，0，0）且母线的方向数为1，1，1；容易得到过原点且与母线x=y=z垂直的平面方程为：

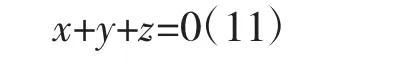
该平面与母线x+1=y=z-1与x-1=y+1=z-2的交点分别为（-1，0，1）和。容易知道，点（1，0，0）与点（0，0，0），（-1，0，1），不共面，所以过这四点存在一个球面，设这个球面的方程（经过原点）为

从而圆柱面的一个准线方程为

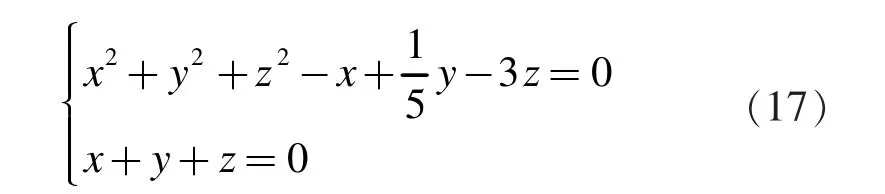
而母线的方向数1，1，1为已知。设M1（x1，y1，z1）为准线上任意一点，则过点M1的母线为

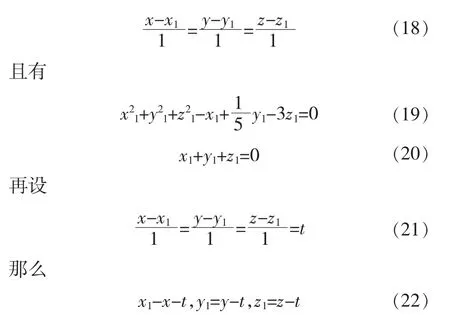
将式（22）代入式（19）和（20）得

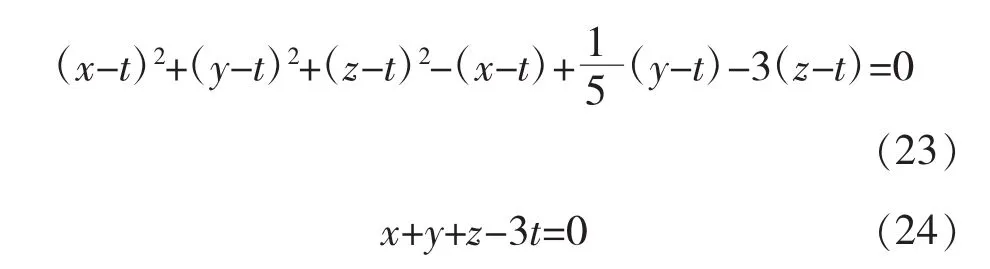
由式（24）得到

将式（25）代入式（23），整理化简即得圆柱面方程（10）。

应当注意，对于方法二，所求的球面方程（16）不是惟一的，也就是说，当我们在决定球面方程时，点（1，0，0）的选择具有随机性，只要所选择的这个点与点（0，0，0），（-1，0，0），不共面，均可作为决定球面方程四个点中的一个，虽然得到的球面方程不同，但并不影响最终的圆柱面方程。特别地，根据教材[2]，也可以求出平面（11）截圆柱面所得圆的圆心和半径，进而写出柱面的准线方程，具体为

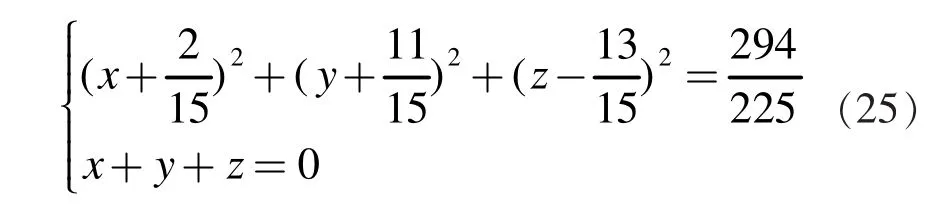
根据上述方法也可以得到柱面方程（10），具体细节可参考教材[2]。

2 结束语

柱面方程的求解是解析几何中的一个重要内容，它充分体现了解析几何是用代数的方法研究几何问题这一数学思想，具有重要的研究意义。文章针对一个具体的柱面-圆柱面，根据其特殊的几何性质，采用两种不同的思想方法求解其方程，对于扩展学生的思维以及理解柱面方程的求解都具有极其重要的意义。