基于HFSS双频带通型频率选择表面的研究

韩丹枫

（长治学院 电子信息与物理系，山西 长治 046011）

随着雷达系统和天线系统的发展，特别军事上对雷达系统隐形的要求越来越高，对天线系统对外界电磁干扰和天线本身的保护，频率选择表面（Frequency Selective Surface即FSS）设备变得越来越重要。FSS是一种周期结构，通常由单层或多层金属贴片与介质构成，对特定频率的电磁波具有过滤筛选作用，此外还有对设备本身具有保护作用，如防止雨水冲洗和腐蚀等。FSS是一般认为是一种无限周期结构，直接进行电磁建模求解较难，但是，Floquet定理指出了周期结构电磁场的特性，使得其求解变容易。文章基于三维电磁仿真软件HFSS的Floquet端口激励周期边界条件，对FSS的结构与其电磁特性进行了研究，最后设计了一种可以同时工作于C（中心频率为6GHz）波段和X（中心频率为10GHz）波段的 FSS。

1 基本理论

FSS本质是一种在电磁空间上的滤波器，其类型与滤波器基本相同，一般分为带通、带阻、高通、低通等类型，通常采用较多的是带通和带阻型两种。本文主要研究带通型FSS，故以带通型FSS为例，进行相关研究和说明，如图1为最简单的带通FSS。

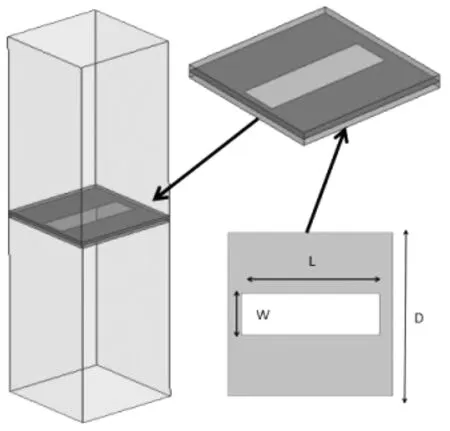
图1 FSS单元模型图

FSS的主要参数与滤波器相同其中重要的参数有S11和S21，S11表示入射波的反射系数，S21表示传输系数[1]，其定义如下：

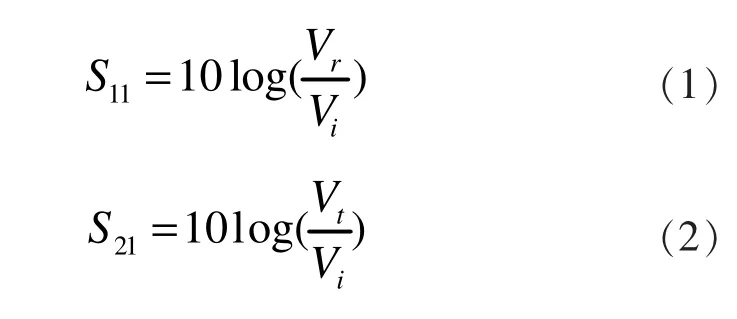
图1所示为FSS的一个单元，影响其主要特性的是镂空单元的长度L，宽度W主要影响带宽，此外介质不仅仅起到固定保护的作用，同样对于FSS的特性也是很重要，主要影响谐振波的波长。

而FSS镂空单元的长度一般约为二分之一谐振波长，即：

整个单元可以是长方形底面，也可以是正方形底面，便于研究，本文为正方形底面，其尺寸由经验公式给出：

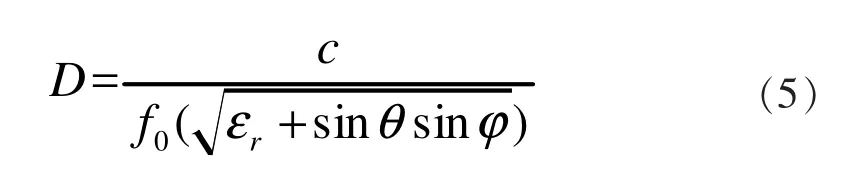
因为入射波表征的电压Vi比传输过去的电压Vt和反射回去的电压Vr都大，所以S21和S11都是负数。当S21越接近0 dB的时候，表示传输过去的信号越多，当S11越接近0 dB的时候表示反射的信号越多。

基于一字带通型FSS对孔径长宽影响仿真分析，结果如下：

（1）对单元长度仿真分析

图2 单元长度的影响

表1 单元长度和对应的中心频率及带宽

通过仿真结果可知，一字单元长度影响的谐振心频率，长度越长，谐振越低，与波长和谐振频率成负相关的特点相吻合。

从带宽上来看，单元的长度对谐振点的带宽稍微有点影响，长度越小，带宽越大，带宽的特性与谐振频率成正相关的特性。

（2）对单元宽度仿真分析

图3 单元宽度的影响

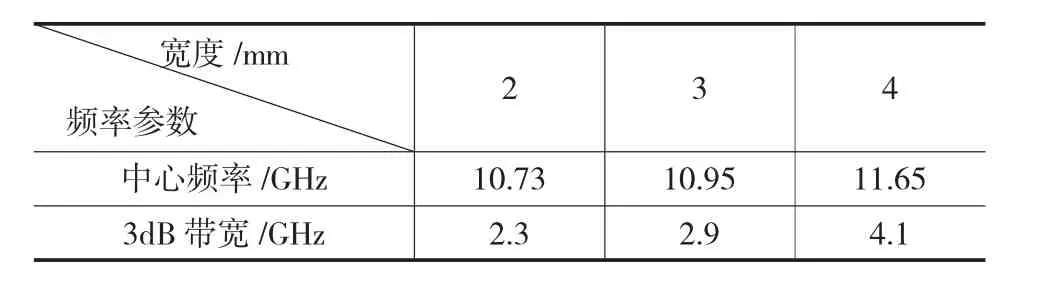
表2 单元宽度和对应的中心频率及带宽

由结果可以看出来，一字单元的宽度对谐振的中心频率并没有影响，它主要是影响FSS的带宽。当宽度越小的时候，3dB带宽越小，宽度变大谐振的带宽也变大。这主要是宽度越大能量透射去的也越多，所以衰减对应越小。

2 建模与结果分析

文章旨在一种工作于C波段和X波段的双频带通FSS，带通滤波器的特性，利用带通滤波器串联的特性，可以实现双频，对照四边形环[2][3]。文章采用双圆环结构单元，进行HFSS建模仿真，利用HFSS自带的优化工具优化。双环FSS单元结构如图4所示。

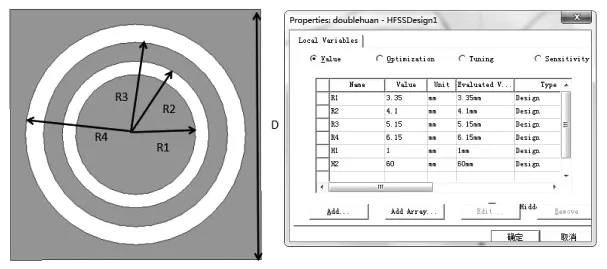
图4 FSS单元结构图和参数

从图4可以看出，在6 GHz和10 GHz处，S11位40 dB以下，说明在这两个频点附近，电磁波几乎可以完全通过，反射很小。且两个中心频点附近，10 dB以下的带宽都有1 GHz左右，能够起到对雷达的保护作用，并且能够过滤其他波段的干扰。

图5 HFSS仿真结果图

3 总结

文章基于HFSS仿真软件，对FSS单元结构对带通特性进行了研究，通过仿真发现，单元长度主要影响谐振的中心频率，单元或者开槽的宽度，影响带通宽度。最后利用无极性的圆环结构，设计了一种可以同时工作于C波段和X波段的FSS，通过仿真和优化，最终确定FSS单元的参数。