钻杆多通道磁记忆检测信号的多方向梯度处理方法

，， ，， ，

(1.中国石油大学(北京) 机械与储运工程学院，北京 102249；2.中国石油天然气股份有限公司 塔里木油田分公司，库尔勒 841000)

由于磁记忆检测技术对应力集中敏感而成为铁磁性构件早期损伤检测的重要方法。铁磁性材料应力和变形的集中区域会在地磁场和工作载荷下发生不可逆的磁畴组织重新排列，导致应力集中区域产生磁场畸变，表面出现漏磁场，再通过对漏磁场的检测来进行应力集中区域的诊断[1]。磁记忆现象的基本理论表明，采用求梯度等信号处理方法可找出法向分量零点或切向分量最大点[2-4]。随着近几年的发展，磁记忆检测已经由单通道检测开始迈入多通道检测，但多通道信号梯度的处理上依然延续以往的在检测方向上求梯度的方法，易造成与检测方向同向的应力集中区域信号反应不灵敏或漏检的问题[5-7]。已有学者研究了采用切向和法向分量两种信号联合进行检测的方法，但这会增加对硬件系统的要求。笔者探讨了一种将切向分量方向与法向分量方向联合梯度求解的方法，某点的梯度由检测方向上的点与垂直方向上等距的点共同求得。对钻杆的磁记忆检测信号进行两种梯度联合求解的处理方法，比只从检测方向求梯度的方法对畸变磁场更为灵敏。

1 现有的多通道磁记忆检测信号梯度算法

现有多通道磁记忆检测信号处理的过程一般为均值降噪、数据归一化及求取检测方向上的梯度。均值降噪是为了剔除信号曲线上的毛刺，即信号中夹杂的高频环境噪声，方便识别磁场畸变信号的突变点；数据归一化是先求取所有传感器整体信号均值，然后将每个传感器信号序列都减去自身均值，即偏移到零轴附近，最后将各传感器信号加上整体均值，以偏移回整体基线附近，达到消除传感器差异的目的；梯度表征磁记忆信号的突变情况，梯度突变点可表征漏磁场的位置，梯度最大值位置可表征漏磁场变化最剧烈的位置。梯度的求解过程为两点间磁场强度H的变化量与两点间距L的比值，梯度的表达式如式(1)所示[8]。

(1)

式中：KN为N点的梯度；HN,HN+i分别为第N点和第N+i点的磁场强度；Lx，N,Lx，N+i分别为第N点和第N+i点的磁记忆信号的位置坐标。

该梯度算法是在检测方向上进行单一的梯度求解(见图1)，假设进行n通道检测，各通道每隔1 mm均采集1个数据点，间隔3 mm进行梯度求解，则第1个通道的第1个点的梯度如式(2)所示，此后窗口依次滑动遍历求取其他位置的梯度。

(2)

可见该梯度的求解过程只与本通道数据有关，与相邻通道无任何关系。当应力集中区域沿检测方向呈细条状且足够长时，该通道漏磁场信号均异常大，但只在该区域的端部产生梯度突变，无法对应力集中全区域产生梯度异常响应，不能很好地反映应力集中区域。应力集中区域与检测方向同向的磁记忆检测示意如图2所示。

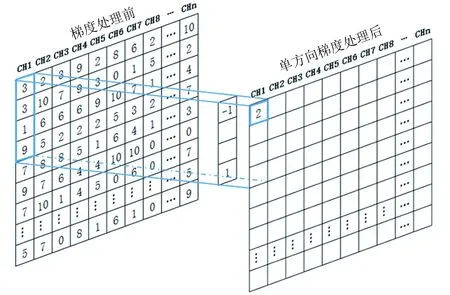
图1 沿检测方向求梯度算法示意

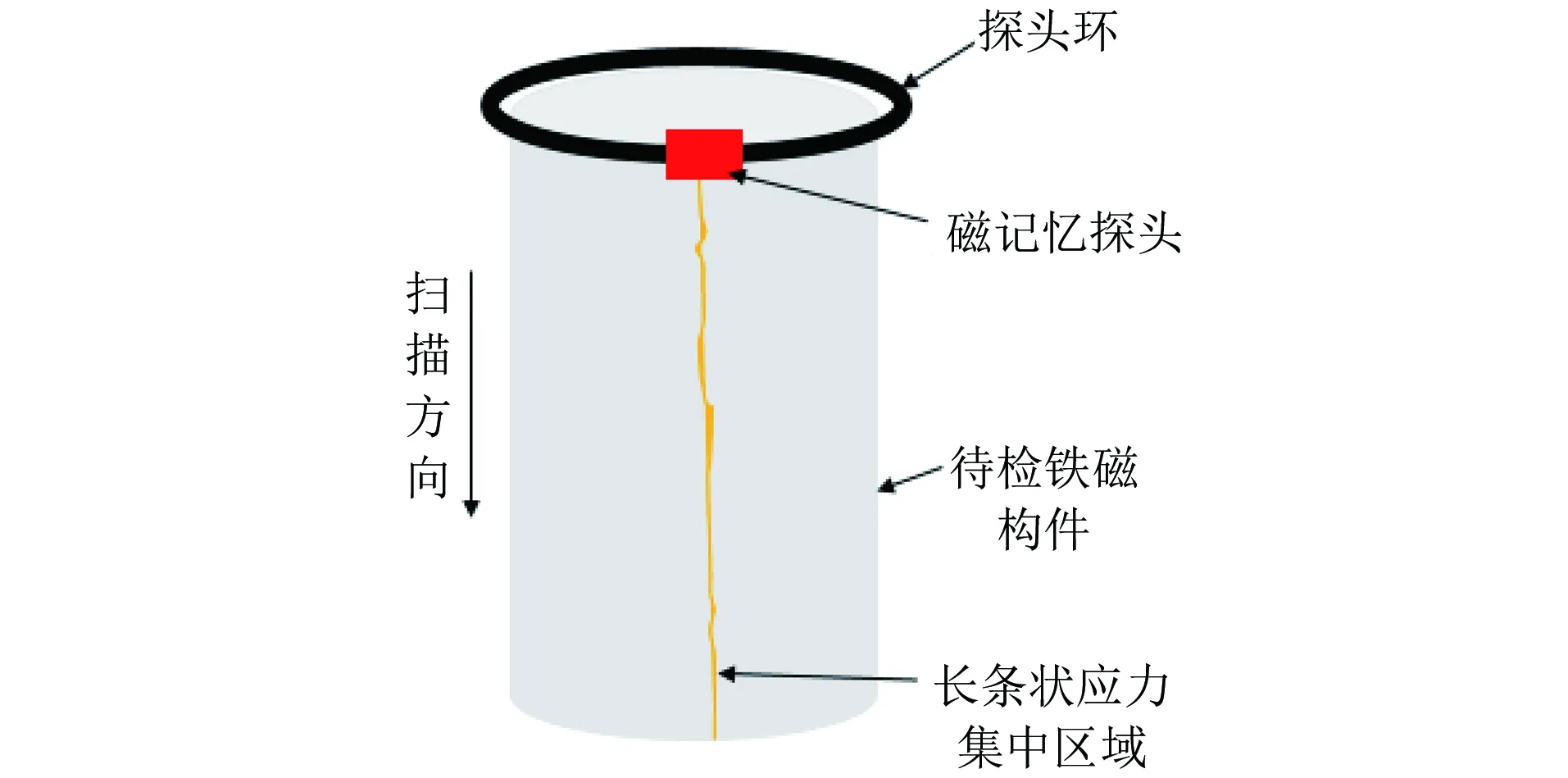
图2 应力集中区域与检测方向同向的磁记忆检测示意

2 多通道磁记忆检测信号的多方向梯度算法

2.1 多方向梯度算法的原理

在多方向上进行梯度求解，指的是每点的梯度求解与4周等距的4个相邻点有关，而非只与检测方向上的本通道信号相关。从检测原理上分析，多方向的梯度值表征该点的漏磁场相对于相邻等距位置的漏磁场的突变情况，不再仅是相对于一点的突变情况，因此从理论上避免了因扫描方向带来的漏检，此时的梯度如式(3)所示。

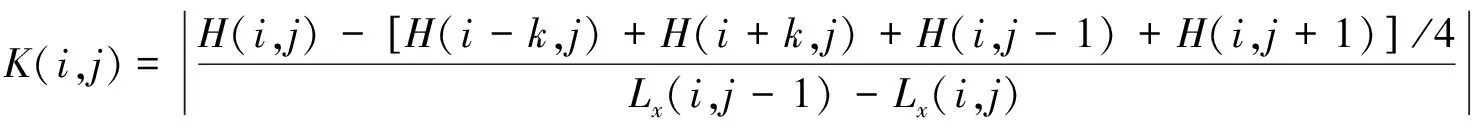
(3)

式中：K(i,j)为第j通道第i点的梯度值；H(i,j)为第j通道第i点的磁记忆信号；H(i,j-1)和H(i,j+1)分别为第j-1和第j+1通道第i点的磁记忆信号；H(i-k,j)和H(i+k,j) 分别为第j通道第i-k点和第i+k点的磁记忆信号，且这两点与H(i,j)的距离等于H(i,j)与H(i,j-1)的距离，即4点与待求点距离均相等；Lx(i,j)为(i,j)点的位置坐标;Lx(i,j-1)为(i,j-1)点的位置坐标。

从数学计算上分析，即通过与待求点上下左右等距的特定梯度的卷积核对信号进行线性卷积。卷积公式[9-10]为

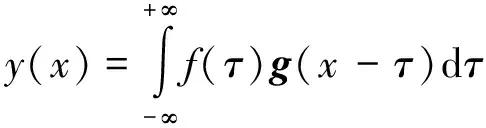
(4)

式中：f为待梯度处理信号；g为梯度卷积核;y为信号梯度卷积值。

2.2 多方向梯度算法的实现

对于n通道，数据长度为m，通道物理间隔为L，单通道采集频率L/k的信号进行数值遍历的算法实现如下所述。

循环i从2到n-1，循环j从k到m。

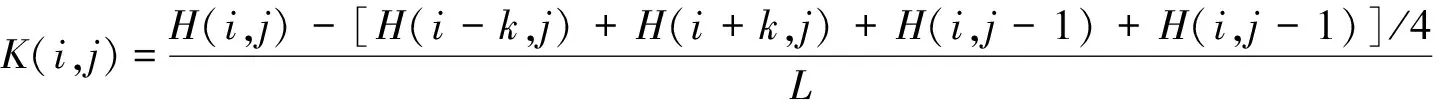
(5)

循环j结束，循环i结束，循环j从k到m。

(6)

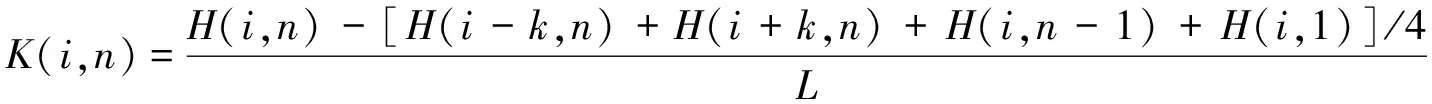
(7)

循环j结束。

对于圆柱形构件，计算第1通道时，应将第n通道和第2通道作为相邻通道处理;计算第n通道时，应将第n-1通道和第1通道作为相邻通道进行处理。对于板型构件，计算第1通道和第n通道时，只需将相邻空区域补0即可。

构造梯度卷积核的方法如下，假设第n通道检测，相邻通道间隔距离为1个距离单位(这里不设具体单位)，各通道每0.5个距离单位均采集1个数据点，为与通道间隔等距，需选定检测方向间隔为1进行联合求解，则梯度卷积核表达式为

(8)

此时的计算过程为梯度处理前矩阵和梯度卷积核矩阵对应位相乘后求和，再除以相邻通道的物理距离，即得梯度处理前矩阵与梯度卷积核交叉部分中心的梯度，多方向求梯度算法示意如图3所示。

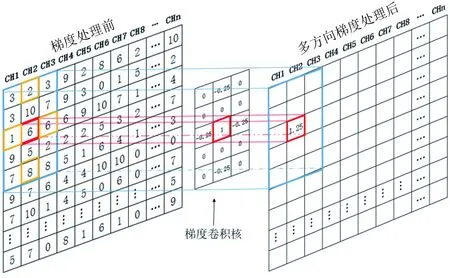
图3 磁记忆检测信号的多方向求梯度算法示意

3 两种梯度算法应用对比

检测装置采用中国石油大学(北京)安全监测与智能诊断实验室研发的16通道钻杆磁记忆检测仪，沿周向均布的磁记忆传感器环在电机驱动下运转，传感器贴合钻杆表面进行轴向匀速扫描，并将钻杆表面磁记忆信号通过无线传送给上位机，多通道钻杆磁记忆检测原理示意如图4所示。

图4 多通道钻杆磁记忆检测原理示意

检测对象为加厚的表面存在由腐蚀坑组成轴向条形腐蚀区域的φ76.2 mm钻杆，将传感器环的第15号通道对准该损伤区域进行检测(见图5)。

图5 钻杆损伤区域实物

将检测信号进行两种梯度算法的处理，每种算法均对梯度进行曲线绘制，结果如图6，7所示。

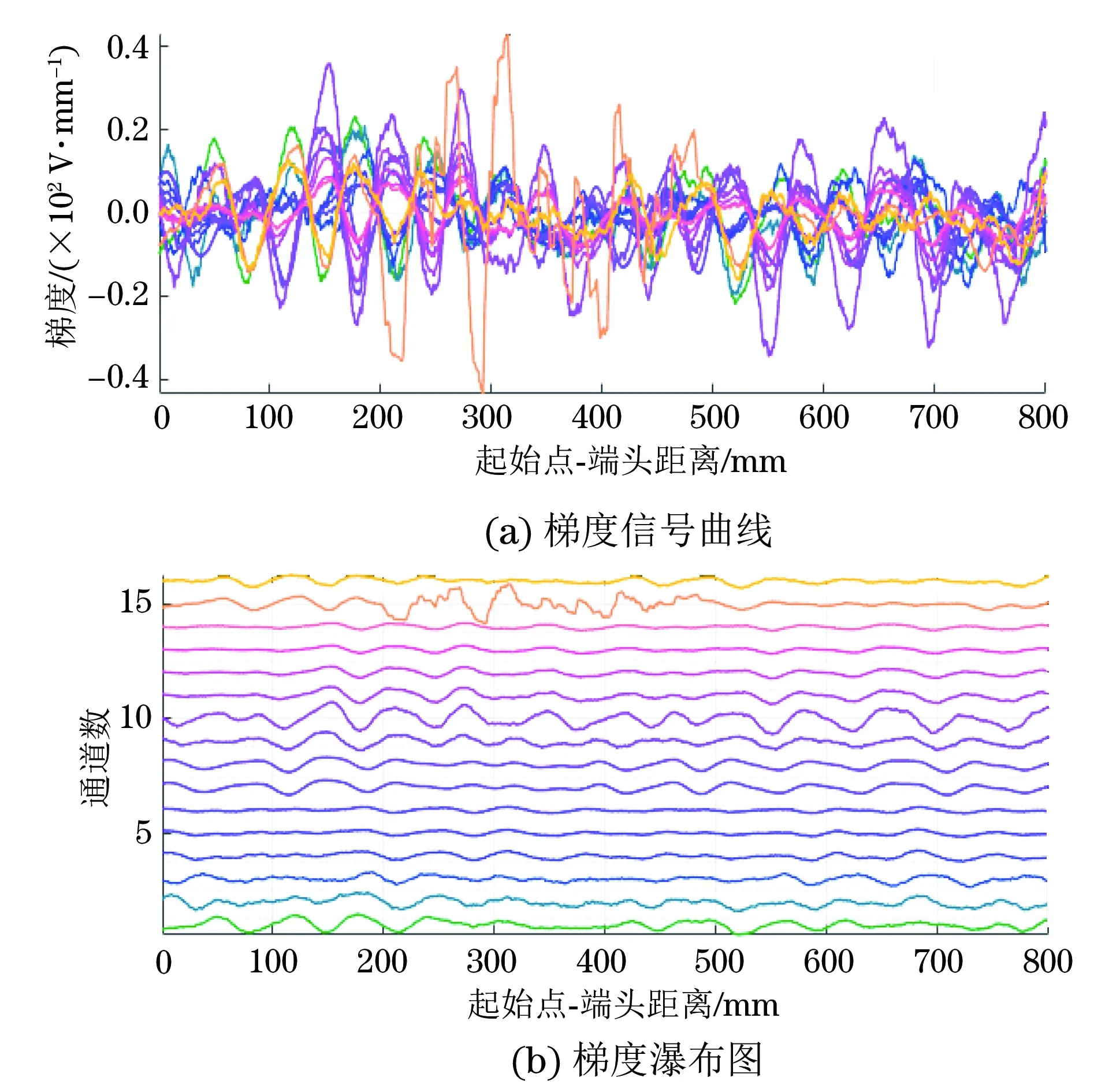
图6 磁记忆检测信号的沿检测单方向求梯度处理结果

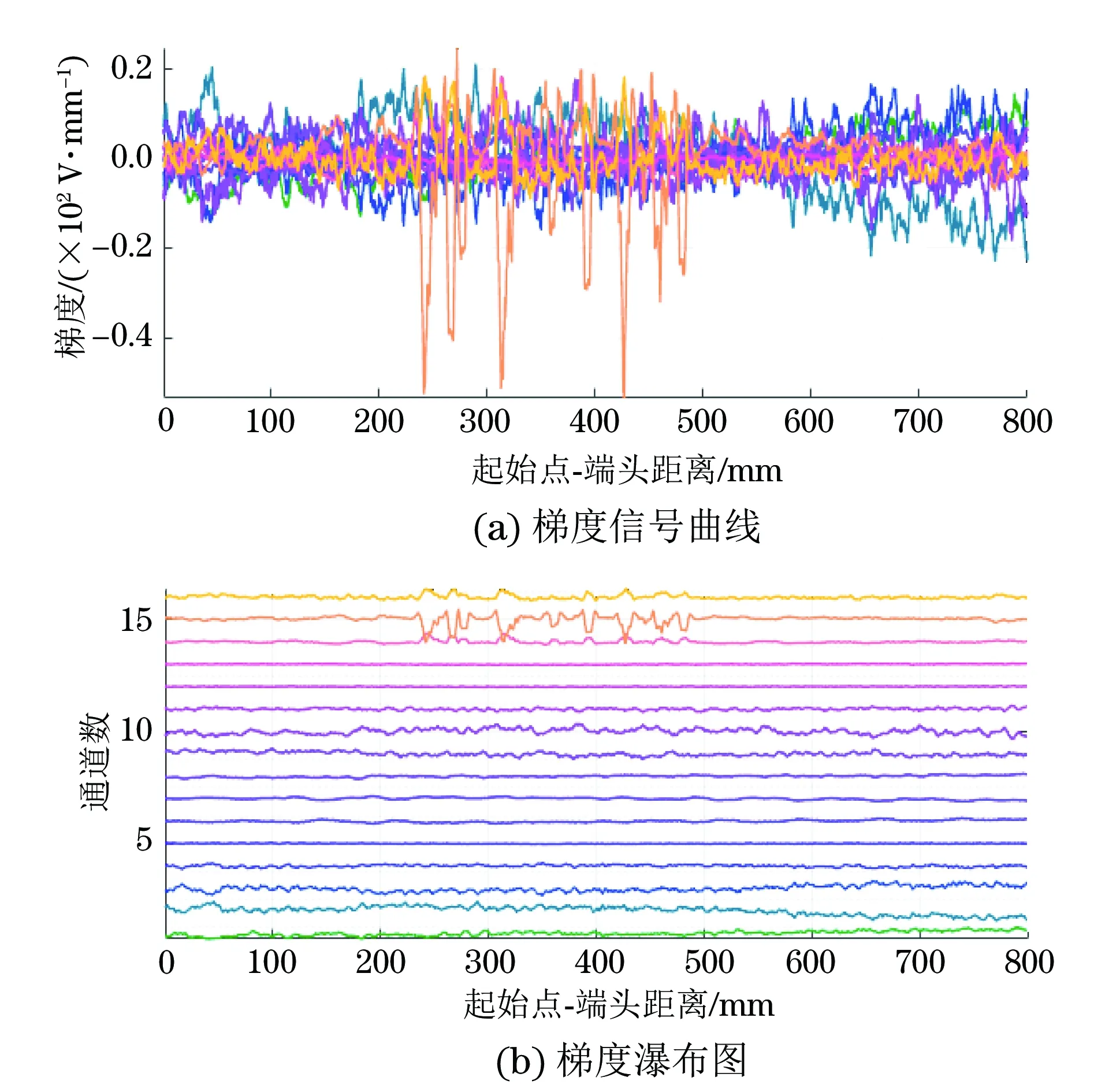
图7 磁记忆检测信号的多方向求梯度处理结果

从图6可以看出，对同一个检测信号数据计算梯度，沿检测单方向求梯度时，梯度只受单数据点的影响，在梯度图上异常部位的曲线显示并不明显；从图7可明显看出，第15号通道信号因为腐蚀坑而剧烈跳动，这是因为该通道梯度求解过程中与相邻的第14，16号通道正常信号相关。对比按照通道进行排列的梯度瀑布图可以看出，单方向求梯度时其他通道均存在低频高赋值跳动，而多方向梯度瀑布图只存在高频低赋值跳动。从梯度瀑布图第15号通道的信号对比可以看出，多方向梯度信号曲线跳动更剧烈，这是因为多方向多点求梯度的过程本身也是对噪声信号的抑制以及对异常信号的放大。

4 结语

对多通道磁记忆信号梯度求解的算法原理和算法过程进行分析，在多通道磁记忆梯度求解过程中采用多方向梯度算法，并通过构造梯度卷积核进行了钻杆磁记忆信号切向分量多方向梯度求解的应用，从理论和实际应用上证明了多方向梯度算法比沿检测单方向求梯度效果更好。给钻具磁记忆检测及圆柱形、板型构件的多通道磁记忆检测信号处理提供了一种参考。

[1] LI C, DONG L, WANG H. Metal magnetic memory technique used to predict the fatigue crack propagation behavior of 0.45%C steel[J]. Journal of Magnetism and Magnetic Materials, 2016, 405:150-157.

[2] DOUBOV A A. The method of metal magnetic memory-the new trend in engineering diagnostic[J]. Welding in the World, 2005, 49(9): 314-319.

[3] 任吉林, 林俊明, 任文坚,等. 金属磁记忆检测技术研究现状与发展前景[J]. 无损检测, 2012, 34(4): 3-11.

[4] 任吉林, 刘海超， 宋凯. 金属磁记忆检测技术的兴起与发展[J]. 无损检测, 2016,38(11) :7-15.

[5] 周成森. 基于梯度法的金属磁记忆检测仪[D].南京：南京航空航天大学,2012.

[6] 栾明, 樊建春, 张来斌, 等. 一种新的多探头金属磁记忆检测仪信号处理方法[J]. 无损检测, 2011, 33(1): 54-57.

[7] 任吉林, 王进, 范振中, 等. 一种磁记忆检测定量分析的新方法[J].仪器仪表学报,2010,31(2):431-436.

[8] 孙玉江,樊建春,祖强,等. 基于磁记忆技术的钻杆检测系统研究[J]. 中国安全生产科学技术,2014,10(9):129-133.

[9] 胡广书.数字信号处理——理论、算法与实现[M].北京:清华大学出版社,2003.

[10] 陈佳益,黄楠,熊刚强，等. 基于置信区间的自适应加权均值滤波算法[J]. 南京理工大学学报,2017,41(3):307-312.