一种单频网模式下无源雷达时域杂波对消算法
2018-03-22,,,,,
, , , , ,
(1. 中国科学院电子学研究所, 北京 100190;2. 微波成像技术国家重点实验室, 北京 100190;3. 中国科学院大学, 北京 100049)
0 引言
外辐射源雷达是一种间接利用第三方非合作辐射源作为照射源的双/多基地雷达,常用的信号包括数字电视、调频广播和全球移动通信系统(GSM)等[1-3]。由于外辐射源雷达本身静默,具有良好的“四抗”特性,在战时存活率高,近年来越来越受到关注。为了解决外辐射源雷达双基地架构分辨率过分依赖几何位置和目标姿态对目标散射截面积(RCS)影响大等问题,可考虑融合多波段/多频道探测信息或者是采用多发多收的分布式探测体制,从而提高目标探测稳定性和跟踪连续性[4-5]。单频网作为新一代数字广播电视被广泛采用是由于其能实现对一定区域的有效覆盖,同时节约频率和功率资源,非常适合用作外辐射源雷达的辐射源。然而,基于单频网的外辐射源雷达具有显著不同于常规外辐射源雷达的特征,面临的问题也更加复杂,主要体现在更严重的直达波和地杂波[6]、单频网模糊问题影响目标判别和定位[7],以及接收站的位置布置等[5]。
文献[6]提出由于数字电视单频网的存在,直达波和回波通道中都包含有多个发射站的同频直达波干扰信号,这些干扰使得直达波通道中的直达波不“纯净”以及回波通道中的信干比较低,通过对直达波通道使用空域滤波的方法获得较为“纯净”的直达波信号,对回波通道通过极化域滤波和频域的多通道NLMS对消算法来抑制回波通道的干扰,从而提高雷达系统在单频网环境下的抗干扰能力。文献[8]指出在SFN中,多个信号从不同的方向照射到目标,极有可能造成大时延扩展。在没有参考信号信息的情况下,提出了在接收通道中利用阵列天线把大时延转化为小时延,建立新的张量接收模型,并利用联合对角化方法同时估计波束、时延和频偏三个矩阵变量,解决频域盲源分离算法在大时延扩展中估计精度不高的问题。文献[9]提出在单频网模式下,移动平台外辐射源雷达中因发射信号为连续波信号,除了受到空时耦合地(海)杂波影响外,还会受到强直达波干扰的影响。由于直达波的存在,参考信号和监测信号相关处理后的基底严重抬高,将严重降低STAP的杂波抑制性。提出了利用扩展相消批处理算法与空时自适应处理联合抑制直达波和地杂波的方法。
在实际单频网系统中,由于多个发射塔中滤波器等模拟器件存在差异性,器件的量化误差、制造公差、装配误差、天线在长期使用过程中产生的热变形等因素的影响,通道不可避免地存在通道幅相误差[10-12],导致单频网模式下各发射塔各自发射的信号间存在去相关,而此时彼此存在去相关的信号被外辐射源雷达接收系统接收,分别作为参考信号与回波信号。由于参考信号与回波信号彼此间信号产生了去相关,外辐射源雷达杂波对消性能将受到严重影响。
针对单频网模式下信号产生去相关效应,目前的研究工作尚属空白。本文将首先介绍在单频网模式下各发射塔信号彼此产生去相关的模型,在这种情况下,对已有的杂波对消算法包括扩展相消批处理算法和归一化最小均方误差算法进行了杂波对消性能分析。针对已有杂波对消算法对消性能下降严重的问题,在NLMS算法的基础上,提出了一种单频网模式下基于NLMS的无源雷达杂波对消算法,在理论分析和实例仿真的基础上验证了改进算法的有效性,为单频网信号去相关这一问题造成杂波对消性能下降提供一种解决方案,也为基于单频网的外辐射源雷达提供一定的理论指导。
1 单频网信号去相关模型
在单频网信号去相关模式下,回波信号中含有多个发射塔发射的去相关信号,包括直达波信号、多径干扰信号、目标信号等。回波信号可以看作是多个不同直达波信号及其本身延迟的加权求和。回波信号可表示为
(1)
式中:xi(n)为来自第i个发射塔的直达波信号;N和K分别为发射塔的个数和对应每个发射塔的多径干扰个数;nj为各路径相对于最先到达的直达波信号(假设时延为0)的相对时延;αj为各路径信号相对于最先到达的直达波信号(假设幅度为1)的系数;ξ(n)为总的等效噪声。
为了方便研究,暂时仅考虑有两座发射塔构成单频网的情况,参考通道接收的信号仅含有两路直达波,回波通道含有两路直达波及其对应的多径杂波。单频网信号去相关模式下系统工作原理如图1所示。

图1 单频网信号去相关工作原理图
由文献[13]可知,滤波器传输函数可以表示为
Hij(f)=M+Tcos(2πvf+θ)
(2)
式中,v为幅度波动的“频率”,i为接收通道,j为同一接收通道中滤波器的序号,M为天线阵元个数,T为实数。波动指的是“峰-峰波动”,用A表示,它与M和T有如下关系[13]:
A(dB)=20lg[(M+T)/(M-T)]
(3)
2 已有杂波对消算法
2.1 算法描述
在外辐射源雷达中,武汉大学[9]通过分析运动平台的杂波空时特性指出,在进行空时自适应处理前需要消除直达波和强杂波干扰,首次在ECA算法的基础上提出了ECA-B算法,该算法主要通过将信号投影到杂波信号正交的子空间,以达到抑制杂波多径的目的。相对于ECA算法,通过分段的方式把数据分别进行ECA处理,这种分段方式实质并未改变算法总体的计算量,但这能够使用并行处理,使得改进后的ECA-B计算效率大大提升,以适用于大带宽和高阶数的杂波对消。
相比于ECA-B算法,LMS[14-15]类算法是一种沿着权值梯度估计值的负方向进行搜索,逐渐逼近维纳最优解,实现最小均方误差意义下的自适应滤波算法。该算法的优点是运算量较小、结构简单而且实现容易。实际中常用的为归一化LMS(NLMS)自适应对消算法,其利用瞬时平方误差作为滤波器均方误差的简单估计,通过将输入参考信号的功率值引入权值更新过程,能够保证梯度搜索不会发散,并且加速收敛。
2.2 算法仿真
为了比较ECA-B算法和NLMS算法在单频网信号产生去相关时的杂波对消性能,在初始条件相同的前提下,对上述算法分别进行仿真分析。假设回波通道中杂噪比(CNR)为40 dB,通道带内频率波动为1 dB,此时两通道信号的相关系数为0.999 2。ECA-B算法仿真参数如下(此时仿真性能最佳):分段数b=100,对消的距离单元范围为0~200,由于是静止平台,多普勒频率为0。NLMS算法仿真参数设置如下(此时仿真性能最佳):对消阶数设为L=2 048,步长设置选取最佳。采用ECA-B算法和NLMS算法的对消结果分别如图2(a)和图2(b)所示。可以发现此时ECA-B算法的对消比为36.3 dB,比理论值低3.7 dB,没有达到理论对消结果;NLMS算法的对消比为36.2 dB,比理论值低3.8 dB,也没有达到理论对消结果。

(a) ECA-B算法

(b) NLMS算法图2 回波信号对消输出信号的功率比较
为了进一步验证上述两种算法对目标检测性能的效果,需构造回波信号,假设回波信号仅含有一个目标,其时延所处的距离单元为100,多普勒频率为120 Hz,目标信噪比(SNR)为-40 dB。将参考信号与杂波对消输出信号进行相干积累,时间为1 s,获得雷达的互模糊函数如图3所示。由于本文采用的辐射源信号为数字电视信号,带宽B为8 MHz,理论上目标信噪比提升可由公式10lg(BT)计算得出,其中B为带宽,T为相干积累时间,则相干积累1 s时目标信噪比提升为69 dB。由于仿真中设置的起始目标信噪比(SNR)为-40 dB,故最终目标信噪比理论值为69 dB+(-40 dB)=29 dB。
其中,图3(a)为采用ECA-B算法的结果,图3(b)为采用NLMS算法的结果。采用ECA-B算法时,参考信号与杂波对消输出信号作互模糊函数的底噪为182.0 dB,目标峰值功率为206.9 dB,计算出目标信噪比为24.9 dB,比理论值29 dB低4.1 dB。而采用NLMS算法时,参考信号与杂波对消输出信号作互模糊函数的底噪为182.2 dB,目标峰值功率为207.6 dB,计算出目标信噪比结果为25.4 dB,比理论值29 dB低3.6 dB。

(a) ECA-B算法
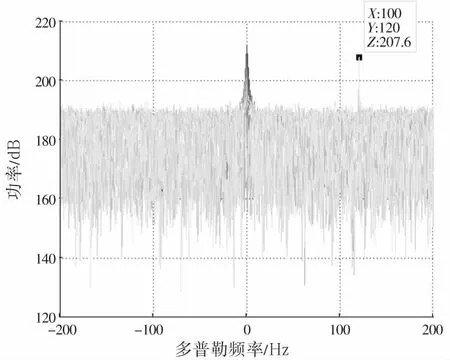
(b) NLMS算法图3 互模糊函数结果
比较NLMS算法和ECA-B算法可知,无论采用何种算法,均不能使对消达到理想,均有较大的对消残余。为了提高杂波对消性能,必须对现有算法进行改进,使得对消性能接近理论值。由于ECA-B算法需要矩阵求逆,计算量很大,复杂度很高,对于大带宽信号和高阶数杂波不太适用,虽然分段提高了数据的计算效率,但是也带来了问题。一是分段后各数据处理时多普勒分辨率会降低,对消后在多普勒方向产生一个凹槽,分段数越多,凹槽越宽,多普勒单元附近的单元会被消弱[16];二是当分段数不合适或过大时,在对消距离单元内的目标会产生调制作用,在目标所在的距离单元沿着多普勒方向等间隔产生虚警,影响目标检测[17]。同时,由于NLMS算法计算量较低,由上面仿真可知,在对消性能及目标信噪比上,NLMS算法和ECA-B算法实现效果差不多,故以下将对NLMS算法进行改进,以使得对消性能接近理论值。
3 改进的NLMS算法
由于现有杂波对消算法NLMS不能在单频网信号去相关模式下使对消比达到理论值,比理论值低3.8 dB,还有很大的提升空间。为了提高对消增益,需对现有杂波对消算法进行改进,使对消比尽可能的逼近理论值。为了更好地理解改进的NLMS算法原理,首先将对NLMS算法原理进行介绍。
3.1 NLMS算法介绍
在外辐射源雷达中,假设参考信号为SRef[n],期望信号为SEch[n],误差信号为SCcl[n],则NLMS自适应滤波的算法流程如下:


(4)
式中,L为滤波器阶数,即杂波对消时需要对消的距离单元数,x(n)为外辐射源雷达系统中的参考信号SRef[n],w(n)为加权向量,H表示向量的共轭转置,*表示复数共轭。
2)计算误差信号SCcl[n]:

(5)
式中,SCcl[n]为杂波对消结束后滤波器的输出信号,理论上仅含有目标信号和噪声信号,但实际中由于未完全对消,有杂波残余。
3)更新NLMS自适应权值:
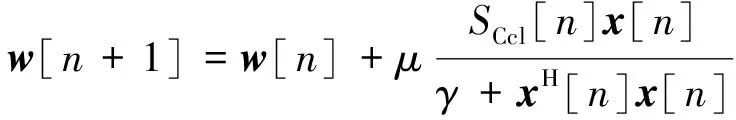
(6)
这是NLMS算法能自适应对消的最关键的一步,利用误差来更新权值,进而逼近维纳滤波的最优解。其中,μ是步长因子,控制算法的稳定性和收敛速度,通过对输入信号功率的计算,本质上也属于一种变步长算法。
假设λmax为输入参考信号x(n)的协方差矩阵的最大特征值,则μ应满足

(7)
LMS算法的原理框图如图4所示,自适应对消器的阶次一般取1 000~3 000,这样在对消掉直达波信号的同时,也能够较好地对消近距离一定范围内的多径杂波。

图4 LMS自适应滤波原理框图
3.2 改进算法描述
考虑到回波通道中包含两路直达波及其对应的多径杂波分量、目标及噪声,为便于分析,此处忽略目标信号及噪声对杂波对消这一环节的影响。故回波信号由式(1)可以改写为


(8)
式中,SRef1(n-ni)为回波通道中接收到的发射塔1发射的直达波1及其对应的杂波多径,ni为杂波多径相对于直达波1到达接收通道的时延,SRef2(n-nj)为回波通道中接收到的发射塔2发射的直达波2及其对应的杂波多径,nj为杂波多径相对于直达波2到达接收通道的时延,w1(i)为对应直达波1及其多径杂波的幅度,w2(j)为对应直达波2及其多径杂波的幅度,i=0,1,2,…,K,j=0, 1, 2, …,N。
由于现有的参考通道是两路直达波的混合,再经NLMS算法对消,滤波器权系数为整体混合后折中值,所以对消结果不理想。观察式(8)可以发现,只要能够单独地获得直达波1和直达波2,先采用直达波1作为参考信号,与回波信号作杂波对消,此时杂波对消输出结果为直达波2及其对应的多径杂波;再采用直达波2作为参考信号与上一次杂波对消输出再作一次杂波对消,此时杂波对消理论结果为仅含有目标信号和噪声,相当于采用现有的杂波对消算法NLMS作了两次对消,这样会增加整体处理时间,不可取。
为了缩短处理时间,进一步对上述设想进行分析,采取两路直达波信号同时分开输入,且滤波器权系数为各自输入信号的最佳权系数,那么这样不仅可以缩短上述两次采用杂波对消的时间,还可以使各自输入的滤波器权系数达到最佳,从而达到理论对消。改进的NLMS算法框图如图5所示。
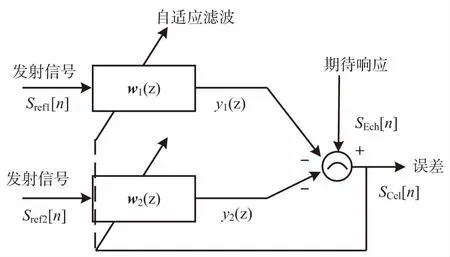
图5 改进的NLMS算法框图
令p为发射信号的数量,wp(n)为第p个子滤波器的权向量,SRef[n]为单频网未发生信号去相关时的参考信号,由NLMS算法原理可以得出发射信号经过权向量后的输出为
(9)
式中,p=1,2。
误差输出信号为
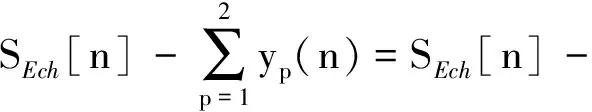
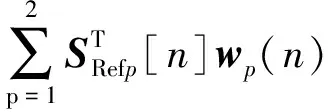
(10)
权系数更新为
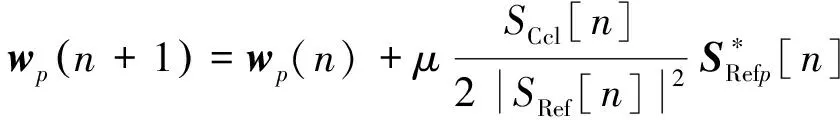
(11)
式中,SRef[n]=[SRef[n],SRef[n-1],…,SRef[n-L+1]]T。
3.3 实例仿真与分析
假设回波通道中杂噪比(CNR)为40 dB,目标信噪比(SNR)为-40 dB,回波信号仅含有一个目标,其时延所处的距离单元为100,多普勒频率为120 Hz,通道带内频率波动为1 dB,此时两通道信号的相关系数为0.999 2。对消阶数设为L=300,采用改进的NLMS算法对消结果如图6所示。此时对消比为39.99 dB,与理论值40 dB基本相等,达到了理论对消效果。
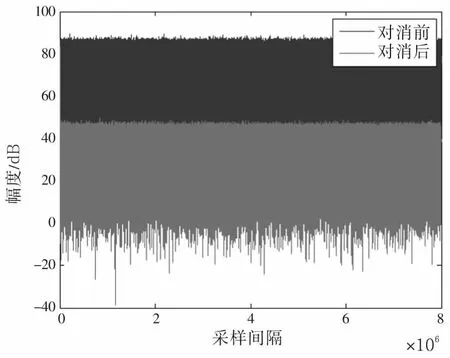
图6 参考信号纯净时采用改进的NLMS算法对消比
由2.2节可知,目标信噪比理论值为29 dB,为了验证最终的目标信噪比与目标理论信噪比之间的关系。将参考信号与杂波对消输出信号进行相干积累,时间为1 s,获得雷达的互模糊函数如图7所示。其中,参考信号与杂波对消输出信号作互模糊函数的底噪为178.7 dB,目标峰值功率为207.5 dB,故采用NLMS算法的目标信噪比结果为28.8 dB,接近目标信噪比理论值29 dB。这也说明了改进的NLMS算法的有效性。同时该算法在对消阶数很低的前提下仍能使对消性能接近理想,更利于工程实时处理。

(a)对消后模糊函数三维图

(b)对消后模糊平面
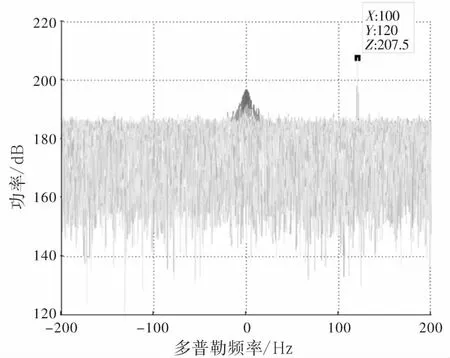
(c)对消后多普勒维图7 参考信号纯净时采用改进的NLMS算法对消结果
以上仿真的前提是改进的NLMS算法输入端假设的是两路参考天线各自接收仅含有对应的一路发射塔信号,但是在实际中,不可避免地会接收两路发射塔发射的信号,对该算法最恶劣的情况便是两路参考天线均接收两座发射塔的信号,同时接收信号的功率相同。下面将考虑在这种情况下,改进的NLMS算法的对消性能及目标信噪比的变化情况。仿真参数保持不变,采用改进的NLMS算法对消结果如图8所示。此时对消比为38.0 dB,与算法未改进时提高了1.8 dB。将参考信号与杂波对消输出信号进行相干积累,时间为1 s,获得雷达的互模糊函数如图9所示。其中,参考信号与杂波对消输出信号作互模糊函数的底噪为180.7 dB,目标峰值功率为207.5 dB,故采用NLMS算法的目标信噪比结果为26.8 dB,与算法未改进时相比目标信噪比提高了1.4 dB。在最恶劣的情况下,对消性能和目标信噪比均有提高,进一步说明了改进的NLMS算法的有效性。

图8 参考信号不纯净时采用改进的NLMS算法对消比

(a)对消后模糊函数三维图
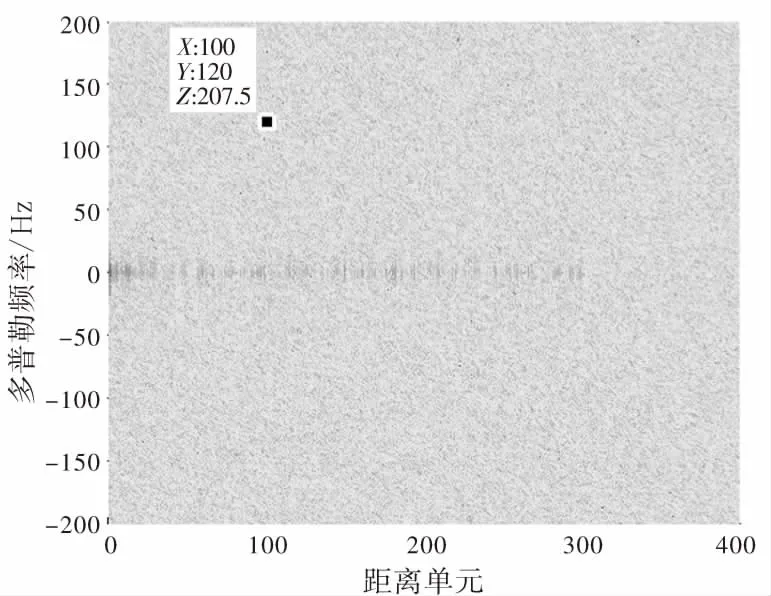
(b)对消后模糊平面
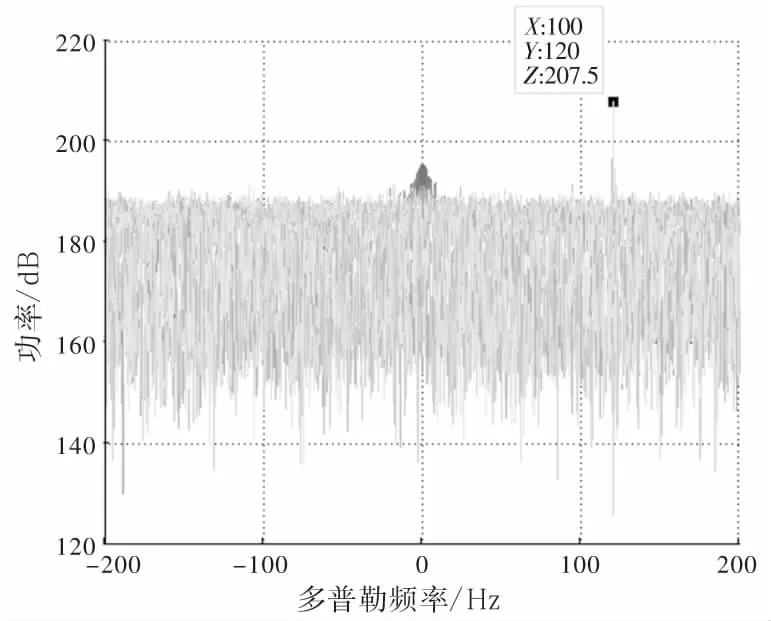
(c)对消后多普勒维图9 参考信号不纯净时采用改进的NLMS算法对消结果
4 结束语
在单频网模式下,由于来自不同辐射源的信号存在去相关,现有的杂波对消算法(ECA-B算法和NLMS算法)难以有效抑制回波信号中的杂波,导致对消性能下降严重。通过分析,本文提出了一种基于NLMS双参考天线的单频网信号去相关杂波对消算法,在理论分析和实例仿真的基础上验证了改进算法的有效性。同时,该算法在对消阶数很低的前提下仍能使对消性能接近理想,更利于工程实时处理,为单频网信号去相关这一问题提供一种解决方案,也为基于单频网的外辐射源雷达提供一定的理论指导。
[1] LU Xiaode, LI Jichuan, LIN Kuan, et al. Range-Doppler NLMS (RDNLMS) Algorithm for Cancellation of Strong Moving Targets in Passive Coherent Location(PCL) Radar[C]∥ International Radar Conference, Lille: IEEE, 2014:1-5.
[2] 杨鹏程,吕晓德,李纪传,等. 基于压缩感知的外辐射源雷达目标检测[J]. 雷达科学与技术, 2015, 13(4):384-389.
YANG Pengcheng, LYU Xiaode, LI Jichuan, et al. Target Detection for Passive Radar Using Compressive Sensing[J]. Radar Science and Technology, 2015,13(4):384-389.(in Chinese)
[3] 柴致海,吕晓德,杨鹏程,等. 无源雷达天线副瓣对杂波对消的影响分析[J]. 雷达科学与技术, 2016, 14(6):568-573.
CHAI Zhihai, LYU Xiaode, YANG Pengcheng, et al. Research on the Effect of Antenna Sidelobe on Clutter Cancellation in Passive Radar[J]. Radar Science and Technology, 2016, 14(6):568-573.(in Chinese)
[4] COLONE F, BONGIOANNI C, LOMBARDO P.Multifrequency Integration in FM Radio-Based Passive Bistatic Radar: Part I Target Detection[J]. IEEE Aerospace and Electronic Systems Magazine, 2013, 28(4):28-39.
[5] 万显荣,易建新,程丰,等. 单频网分布式外辐射源雷达技术[J]. 雷达学报, 2014, 3(6):623-631.
[6] 张曙泽. 基于空域和极化域的数字电视外辐射源雷达干扰抑制研究[D]. 北京: 北京理工大学, 2015.
[7] DAUN M, KOCH W.Multistatic Target Tracking for Non-Cooperative Illuminating by DAB/DVB-T[C]∥ Europe OCEANS, Aberdeen: IEEE, 2007:1-6.
[8] 张各各. 基于盲方法的外辐射源雷达目标探测研究[D]. 西安: 西安电子科技大学, 2014.
[9] 万显荣,梁龙,但阳鹏,等. 移动平台外辐射源雷达实验研究[J]. 电波科学学报, 2015, 30(2):383-390.
[10] 吕孝雷,苏军海,邢孟道,等. 三通道SAR-GMTI误差校正方法的研究[J]. 系统工程与电子技术, 2008, 30(6):1037-1042.
[11] 秦记东,赖涛,赵拥军,等. 基于通道误差校准的空域导向矢量多通道SAR-GMTI杂波抑制方法[J]. 雷达学报, 2014, 3(1):70-77.
[12] 谢斌斌,张骅. 通道误差对波束形成性能的影响分析[J]. 现代导航, 2014(3):192-196.
[13] 冯远. 数字电视辐射源雷达参考信号获取及干扰抑制算法研究[D]. 北京: 北京理工大学, 2014.
[14] SLOCK D T M. On the Convergence Behavior of the LMS and the Normalized LMS Algorithms[J]. IEEE Trans on Signal Processing, 1993,41(9):2811-2825.
[15] ZHAO Y D, ZHAO Y K, LU X D, et al. Block NLMS Cancellation Algorithm and Its Real-Time Implementation for Passive Radar[C]∥ IET International Radar Conference, Xi’an: IET, 2013:1-5.
[16] COLONE F, O’HAGAN D W, LOMBARDO P, et al. A Multistage Processing Algorithm for Disturbance Removal and Target Detection in Passive Bistatic Radar[J]. IEEE Trans on Aerospace and Electronic Systems, 2009, 45(2):698-722.
[17] 方亮,万显荣,易建新,等. 外辐射源雷达扩展相消批处理杂波抑制算法的调制补偿[J]. 电子与信息学报, 2014, 36(1):209-214.
