微重力下离心式锥形两相洗衣机流场的数值模拟研究

苏引引，吴 笛，段 俐，康 琦，吕佩师，许 升，劳春峰，宋华诚，张静静

（1.中国科学院力学研究所国家微重力实验室，北京100190；2.青岛海尔智能技术研发有限公司，青岛266101）

1 引言

换洗衣物的处理给航天员空间站长期驻守带来很大挑战，大多时候，特别是航天员中短期空间飞行需要换洗的衣服当垃圾进行处理。但是衣服的一次性使用将带来极大的资源浪费，按三人在轨飞行180天计算，如采用一次性服装，共需消耗服装300 kg左右，而通常发射1 kg的物品耗费至少1万美金［1］。为了满足航天员太空长期生活对服装生理和心理上的需求，衣服的清洗和重复利用研究具有十分重要的意义。因此，设计一款能耗低、易操控、结构简单和安全性高的空间洗衣机具有重要的实用价值。

空间微重力环境，重力水平是地球表面重力g的10－3～10－6倍，在极低重力水平情况下甚至达到可以忽略的地步，此时表面张力会占主导地位，而微弱的表面张力使流体位形在外力作用下极易发生变化，因此空间流体管理与控制是一个重要而又复杂的问题［2］。如图1所示，航天员在国际空间站上拧毛巾［3］，毛巾中的液体不再同地面受到重力作用一样自由下落，而是在液体表面张力和粘性力的作用下附着在毛巾表面，这种现象导致微重力环境下衣物脱水过程带来困难。同时微重力环境下重力引起的浮力效应消失导致气体和液体混合在一起，如何实现有效的气液分离是清洗衣物亟待解决的问题。

图1 航天员在空间站上拧毛巾［3］Fig．1 Astronaut wringing towels on space station［3］

1990年，美国宇航局（NASA）与俄勒冈州UMPQUA研究公司签订合同共同开发一款新型的太空洗衣机SinglePhaseSpaceMachine（SPSM）［4］，如图2 所示。 SPSM 在衣物清洗过程中采用排除容器中气体保留单相液体清洗解决了气液混合问题，利用微波干燥减少能耗。通过内部囊膨胀排气，往内腔充满洗涤液，通过活塞的上下运动使衣服翻滚，最后再次通过内部囊膨胀排除废水，利用微波干燥达到清洁衣服的目的。1993年，UMPQUA又提出了一种改进型的单相液体洗衣机方案 Single Phase Space Laundry（SPSL）［5］。2012年，美国德州农机大学（TAMUK）的Victoria Bailey等开发了Gravity Independent Laundry System（GILS）［1］，如图3所示。 GILS 利用气囊收缩扩张对衣物挤压，水管喷水和循环加热对衣物进行清洁，给出了微重力条件下的一套高效安全的洗衣流程。

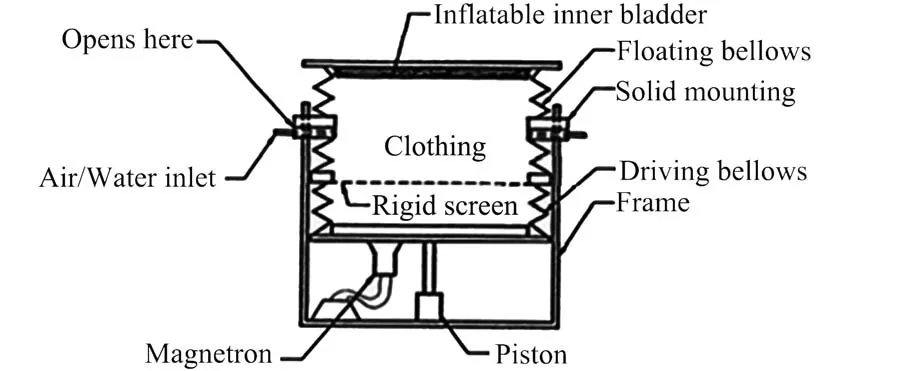
图2 UMPQUA开发的SPSM［4］Fig．2 SPSM designed by UMPQUA［4］

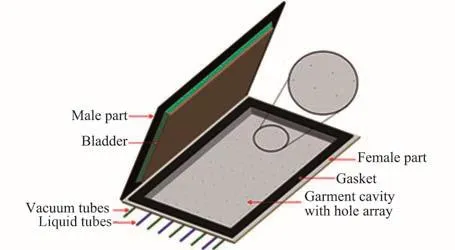
图 3 TAMUK 开发的 GILS［1］Fig．3 GILS designed by TAMUK［1］

本文基于离心式锥形两相洗衣机的设计方案，利用FLOW⁃3D流体力学软件对微重力环境下洗衣机内部流场进行数值仿真，针对失重条件下锥形桶内的流体静态分布、筒／波轮旋转时的动态界面形貌和动态流场分布等关键的微重力流动管理问题［6］开展研究，得到洗衣机滚筒与波轮不同的运行工况的内部流场分布规律，为微重力洗衣机的设计和性能优化提供参考，为在轨清洁技术的开发提供建议。

2 数学物理模型

2.1 计算模型

本文提出一种适应微重力环境的离心式锥形两相洗衣机方案，图4为新型洗衣机简图。当洗涤桶旋转时，离心力的作用使衣物和水汇集到波轮处，通过波轮与衣物之间的相对运动摩擦衣物达到清洗的目的。脱水过程中洗涤桶旋转，由于洗涤液密度大于内部气体密度，产生的较大离心力使液体靠近壁面通过上方的气液出口流出，达到气液分离的目的，而洗涤桶内流体能否有效管理是这种新型洗衣机在微重力环境下能否达到其设计目的的重要保证。

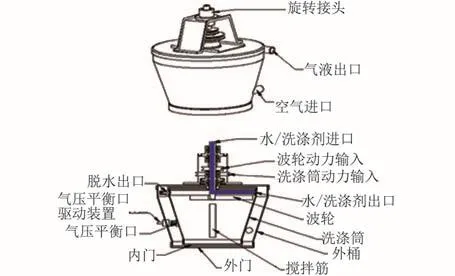
图4 离心式锥形两相洗衣机模型Fig．4 Centrifugal cone⁃shaped two⁃phase washing machine

本文研究离心式锥形洗衣机在空间微重力下气液界面的两相流问题，计算模型如图5。波轮半径R1＝155 mm，滚筒底部半径R2＝100 mm，滚筒高h＝200 mm，初始时刻液体填充高度hw＝68 mm。当波轮和洗涤筒分别以角速度ω1和ω2旋转，洗衣液随着滚筒旋转，在粘性力的作用下流动，离心力沿滚筒壁面分量的作用使液体沿着滚筒壁接近波轮，最后滚筒和波轮共同作用于流体。数值计算基于以下基本假设：1）液体为不可压缩流体，具有恒粘性，恒密度，不受温度、时间的影响；2）不考虑容器与液体的热交换；3）空间环境中的微重力水平在10－5～10－3g0。为了得到洗涤筒与波轮的不同运动方式对流场的影响，借鉴地面洗衣机的实际设计经验，选取了6种不同的工况进行计算，得到洗衣机静态流场，以及滚筒和波轮不同的转速、不同转向下洗衣机动态流场，如表1所示。

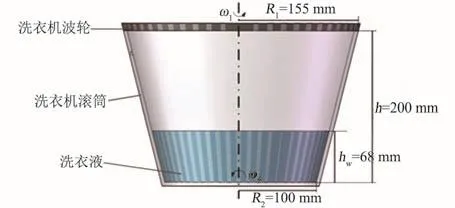
图5 洗衣机计算模型示意图Fig．5 Calculation model of washing machine

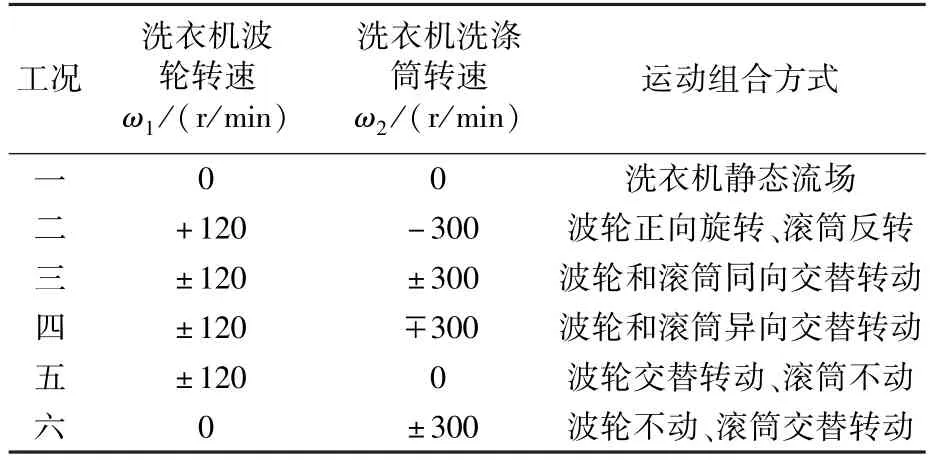
表1 数值模拟不同的工况组合Table 1 Different working conditions of numerical sim⁃ulation

流场中的Bond数和 Reynold数分别如式

（1）、式（2）：

其中，Δρ为界面分割的两种不相容介质的密度差，对于空气⁃洗涤液来说，Δρ近似等于洗涤液的密度ρ，g是加速度，L是特征尺度，取滚筒底部半径R2，σ是界面的表面张力，U取给定工况五滚筒壁面液体速度。洗衣液的物性参数如表2，其中表面张力系数和接触角利用中国科学院力学研究所微重力实验室全自动光学表面张力接触角仪分别采用悬滴法和坐滴法测量［7］。为了便于与实验结果对比，物性参数的测量基于PMMA（有机玻璃），表面张力系数测量精度为10－5N／m，接触角精度为0.1°。

表2 计算模型中洗衣液的物性参数Table 2 The physical properties of fluid in calculation model

由式（1）可知Bo＜1，模型中表面张力占有重要的作用，由式（2）可知Re＝21 174，所以可以看成充分发展的湍流，因此模型中惯性力起重要作用。

2.2 控制方程与边界条件

基于2.1中给出的计算模型基本假设，可以得到不含能量方程的流体力学控制方程，如式（3）、式（4）：

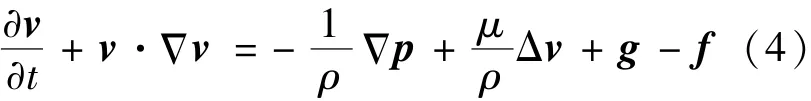
式中，v＝（u，v，w）为流体运动的速度矢量，g为重力加速度矢量，g＝－gez，ez为z方向的单位矢量，f为流场内体积力项，p为压强，ρ为流体密度，μ为流体的动力粘度系数。边界条件如下：

1）洗涤桶和波轮处为固壁边界条件，如式（5）：

式中，n为固壁的单位法向量，包含垂直于波轮和洗涤筒壁面边界的速度分量为零；

2）流体相对于壁面无滑移，即沿壁面两个速度分量为0；

3）流体与壁面之间接触角为0°；

4）在气液界面上，满足法向应力与切向应力平衡条件。

2.3 数值计算方法

本文计算模型的求解方法是由Hirt和Nicho⁃las等人［8］提出的基于多相流体积分数方法（Mul⁃tiphase Volume of Fluid， VOF），通过对整个计算空间的某一相体积分数进行求解获得空间某一相的分布，同时获得相界面的所在位置。液相的体积分数满足式（6）所示方程：

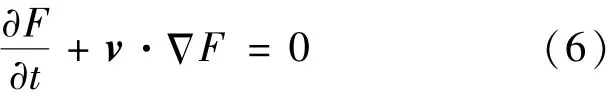
其中，F ＝F（x，y，z）为流体体积函数，表示计算区域内流体所占据的体积分数。若F＝0，则该单元全部为气相流体所占据；F＝1，该单元为液相流体占据；当0＜F＜1时，则该单元为包含两相物质的交界面单元。

本文采用RNG k⁃ε湍流模型进行计算。RNG k⁃ε 模型［9⁃10］源于严格的统计技术，在更广泛的流动中具有更高的可信度和精度。此外，由于计算模型中表面张力占有比重较大，所以计算网格采用六面体结构网格，计算域的网格总数为646 866个，网格平均间距为d1＝3.33 mm。为了验证网格无关性，取网格平均间距为d2＝3.0 mm的划分方式，洗衣机静态流场工况的压力场进行对比。当 t＝1.2 s时，点（0.192，0.07，0.525）的压强分别为 p1＝0.2709 Pa，p2＝0.2673 Pa。 其相对误差为1.3%，可以认为计算结果对网格敏感性较低。

3 计算结果与讨论

3.1 洗衣机静态流场

微重力下重力影响很小，表面张力和粘性力的作用使洗涤桶流场出现与地面环境不同的位形。计算内部流场在微重力环境下的静态分布，对锥形洗衣机进气口、气液出口和气压平衡口位置的选择具有重要的意义。微重力环境下洗衣机开孔处由于尺度小，会产生表面张力驱动力使液体会流入进气口和气压平衡口，影响洗衣机的正常使用。图6是微重力环境下洗衣机底部填充液体后二维自由面重构和压力场（中性截面）。

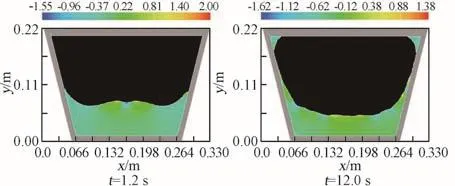
图6 微重力条件下洗涤筒的自由面重构和压力场Fig．6 Surface reconstruction of fluid and pressure of washing tubes in microgravity

微重力条件下，洗衣机底部液体沿着滚筒壁向上爬升在滚筒的中间形成一个凹的自由气液分界面。液体在表面张力的作用下，在液面内外会有压力差，形成附加压强Δp，图7为表面张力引起的附加压力。

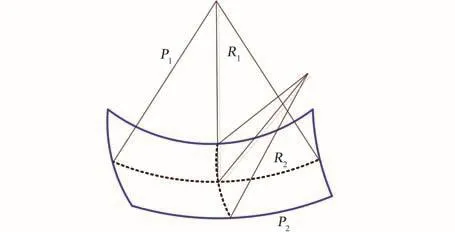
图7 表面张力引起的附加压力Fig．7 Additional tension caused by surface tension

其中，R1和R2是液面的主曲率半径，P1和P2分别为气液内部压强，由 Young⁃Laplace公式［2］得到式（7）：

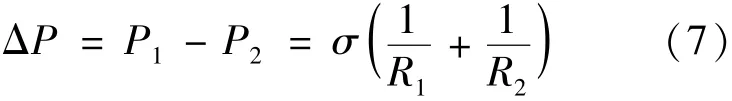
ΔP为气液之间压差。洗涤筒的液面可以近似看成球形的，即R1＝R2＝R。那么靠近洗涤筒中心液面压力差ΔP内和靠近筒壁的液面压力差ΔP外，如式（8）：

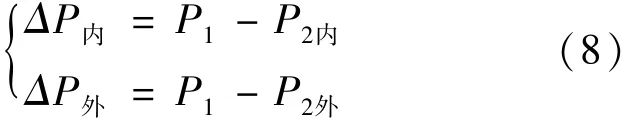
所以毛细驱动力如式（9）：

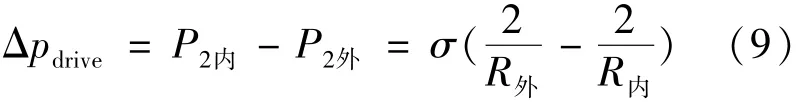
由图6可以看出，由于靠洗涤筒越近液面的曲率半径R外越小，会产生向外的表面张力驱动力ΔPdrive。当t＝1.2 s时，通过云图可以得到靠近旋转轴的液体与靠近洗涤筒壁面压强差ΔPdrive＝1.77 Pa。在表面张力产生的驱动力和粘性力作用下，液体会逐渐浸润整个洗涤筒壁面，当t＝12 s时，液体将气体包裹在洗衣机中心区域。由于洗涤筒开孔处液体受到的表面张力较大，容易沿孔壁流动，为了防止液体从气压平衡口和气口进入外部的气管而影响洗衣机正常使用，在洗涤筒气口的末端（靠近洗涤筒壁处）设计成如图8的结构，并且在楔形处采用与洗衣液接触角大的材料以抑制液体的浸润，减少液体进入气孔。

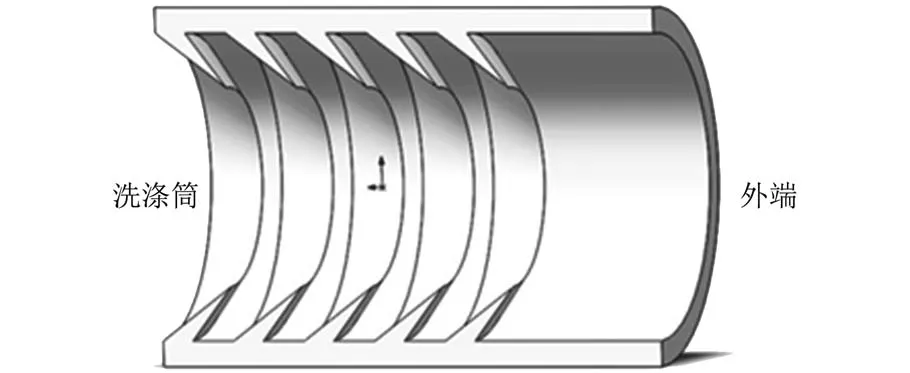
图8 气口处的楔形结构导管Fig．8 The wedge⁃shaped wedge structure in the air pressure balance

3.2 洗衣机动态流场

3.2.1 波轮、洗涤筒单方向旋转

微重力环境下，洗衣机洗涤时内筒旋转，离心力使衣物和水靠近波轮，波轮相对内筒转动，通过波轮与液体以及衣物之间的相对运动摩擦衣物达到清洗的目的。然后波轮与内筒旋转方向改变，使衣物脱离波轮，随后再次接触波轮，以便衣物与波轮充分接触提高清洗效果。通过旋转产生的离心力克服微重力下衣物不能接触波轮导致的机械摩擦力小、洗净度低的问题。

图9是工况二时微重力条件下的流场分布，红色代表液体，蓝色代表气体，截面尺寸与图6一致。波轮和洗涤筒沿着不同方向转动，稳定后的转速 ω1＝120 r／min，ω2＝ －300 r／min，初始时刻洗涤筒波轮的加速为0.3 s，转动停止时减速时间0.3 s，总的计算时间为8 s。

如图9，相比于洗衣机静态流场，洗涤筒从开始运动0.8 s后液体就流到波轮处。在波轮和洗涤筒转速稳定后，当t＝3.2 s时，洗衣机流场在滚筒和波轮的共同作用下达到动态平衡，液体会大部分集中在洗涤筒和波轮结合处，这样在洗涤过程中会使衣物与波轮充分接触，增加摩擦时间提高洗涤效果，在脱水过程中，将出液口设计在结合部更有利于液体流出洗衣机内腔。当t＝4.0 s、5.6 s、7.2 s时，当洗涤筒流场达到动态平衡后，气液界面会形成一个稳定的直径为D的圆柱形液面，8 s左右的时候由于洗涤筒转速降低，液体离心力变小，液体会沿着滚筒壁向下运动，液面直径D会变大，液体会慢慢铺满整个洗涤筒壁。所以在条件允许的情况下尽可能提高洗涤筒的转速，流体会更多地聚集在波轮附近，与衣物之间的交换越好，清洁效果也越好。

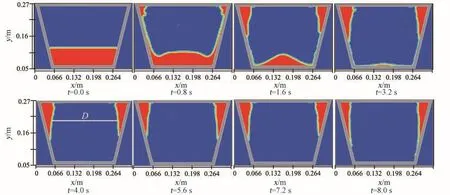
图9 工况二洗衣机微重力条件下自由液面重构Fig．9 Surface reconstruction of fluid of Case II under micro⁃gravity

3.2.2 波轮、洗涤筒交替旋转

流体旋转运动和翻滚运动对洗衣机的性能产生重要影响［11］。流体只旋转不翻滚，衣物膨润不够，舒展不开，冲击无力，洗涤效果不好；如果只翻滚不旋转，同样效果也不好；只有既旋转又翻滚，才能冲击摩擦有力，使洗衣机的综合效能提高。图10是工况三、工况四洗衣机洗涤筒波轮随时间交替运动的转速图，波轮和洗涤筒的加速时间和减速时间均为0.3 s，总的计算时间为8 s，以研究微重力条件下流场的旋转和翻转运动。

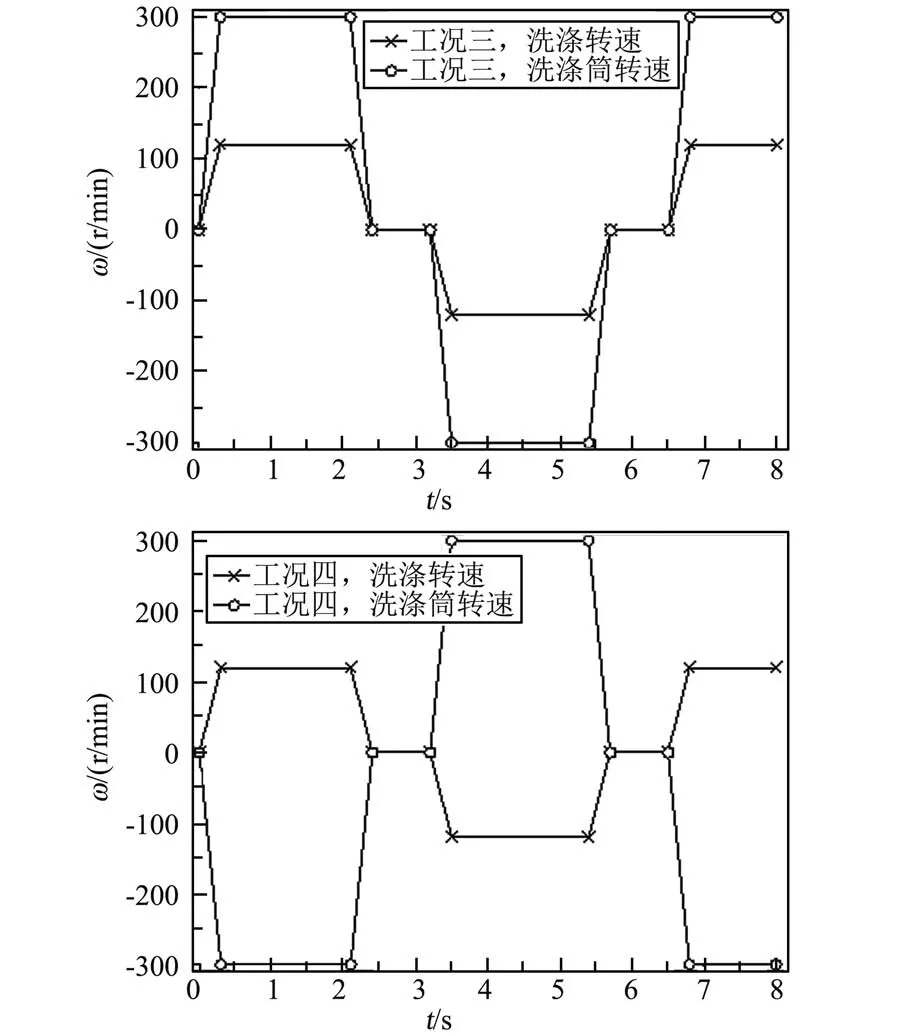
图10 工况三、工况四洗衣机波轮和洗涤筒转速Fig．10 Velocity of washing tube and pulsator of Case III and Case IV

图11 、图12是工况三、工况四微重力条件下，洗衣机洗涤筒波轮随时间交替运动的流场分布，红色代表液相，蓝色代表气相。可以看出，在t＝0.8 s时，与波轮接触的流体较少，波轮的旋转对流体影响比较小，此时的液体位形基本一样。在t＝1.6 s时，明显看到洗涤筒流场下部基本一致，上部当波轮洗涤筒同向转动时，由于波轮的作用使上部圆柱气液分界面直径D明显较大。在t＝3 s时，洗涤筒和波轮转速都变成0，液体内部粘性耗散使流速降低离心力变小，流体会沿着滚筒壁向洗衣机底部运动，最终铺满整个滚筒内壁。滚筒与波轮发生速度反转后，反转初始时刻靠近洗涤筒流体随筒壁转速快，内部流体由于惯性速度比较慢，导致下部分的流体产生较大离心力而突然向上运动，最后形成t＝4 s、7.2 s时流场的翻转，使衣物充分膨润、舒展，提高衣物的清洗效果，同时避免了在清洗过程中只对衣物的某些部位作用而减少衣物的使用寿命。整个过程中流场发生2次流场翻转。

此外，由于流场的翻转，较大的剪切力导致部分流体脱离流场发生了飞溅现象，这样会大大提高洗衣过程中洗涤液对衣物的冲击作用。但在衣物的脱水过程中，为使气液分离更加彻底，保证不出现飞溅现象，洗涤筒需按工况二单一方向运动。

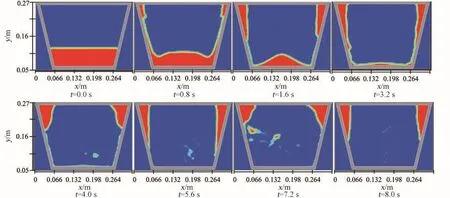
图11 工况三洗衣机微重力条件下自由液面重构Fig．11 Surface reconstruction of fluid of Case III under micro⁃gravity

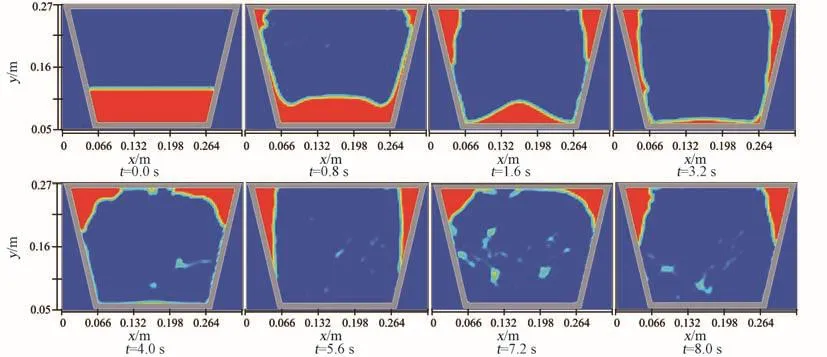
图12 工况四洗衣机微重力条件下自由液面重构Fig．12 Surface reconstruction of fluid of Case IV under micro⁃gravity

3.2.3 滚筒、波轮单一旋转

从简单机械力对洗衣机洗净率与磨损率的影响来看，流体对衣物的冲击力、弯曲力、拉伸力和摩擦力，是提高洗净率和降低磨损率的重要因素。流体作用于衣物的各种机械力，在实际工作中是同时进行的。为了得到微重力条件洗衣机洗涤筒和波轮单一旋转运动对流场的影响，工况五和工况六分别对波轮转速 ω1＝ ±120 r／min、ω2＝0 和ω1＝0、ω2＝ ±300 r／min 进行计算，其中波轮和洗涤筒的加速时间和减速时间均为0.3 s。图13和图14为工况五、六微重力条件下的流场分布。

图13中只有波轮运动时，当t＝0.8 s时，表面张力的作用使流体向洗涤筒底部运动，波轮转动速度并没有对流场产生很大影响。0.8 s以后液体之间的粘性力使远离波轮流体开始转动，最后液体与波轮脱离。相对于工况三和工况四在t＝1.6 s时，流体产生圆柱形气液分界面，且直径D3＞D4，这说明波轮转动会使流体脱离波轮，且波轮与洗涤筒同向转动会加快脱离速度。波轮单独运动时，整个过程中流场没有发生翻转，波轮的运动对于流场翻转没有影响。

图14中，工况六只有洗涤筒交替转动，流场发生2次翻转，且洗涤筒内部流场与工况三和工况四类似。这说明洗涤筒的运动对洗衣机流场分布有重要作用，且决定了流场的翻转效应，而波轮的转动只会影响流体脱离波轮的速度，对流场影响较小，其主要作用是与衣物摩擦而达到清洁的目的。

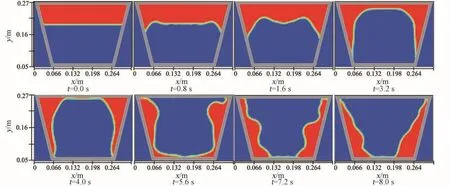
图13 工况五洗衣机微重力条件下自由液面重构Fig．13 Surface reconstruction of fluid of Case V under micro⁃gravity

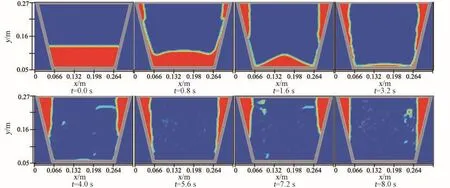
图14 工况六洗衣机微重力条件下自由液面重构Fig．14 Surface reconstruction of fluid of Case VI under micro⁃gravity

3.3 洗涤筒、波轮对流场的作用

3.3.1 洗涤筒、波轮对流场的力的作用

洗衣机通过波轮、洗涤筒的旋转，使洗涤液在桶内形成涡流，迫使织物旋转和翻滚，在织物和织物之间、织物和桶壁之间、织物和洗涤液之间产生摩擦力，同时织物在洗涤液中受到冲击力、弯曲力、压缩力和拉伸力，再加上洗涤液的去污作用，达到洗涤的目的［12］。流体作用于衣物的压力是由洗涤筒和波轮传递的，作用于流场的力越大，流场作用于衣物产生的冲击力越大，洗涤效果就越好［11］。因此得到不同工况下洗涤筒和波轮对流场的力对洗衣机的设计具有重要的意义。图15和图16分别是洗涤筒和波轮对流场产生的力。

从图15、16对比可以看出，波轮和洗涤筒交替旋转的情况下，工况三波轮洗涤筒的同向交替旋转对流场的力F1、F2比工况四波轮洗涤筒的异向交替旋转产生的力都要略大。

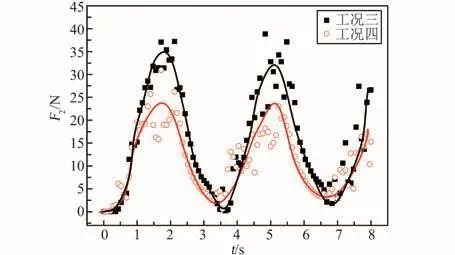
图16 波轮对流场产生的力Fig．16 The force generated by the pulsator

综上所述，为了保证洗衣机在洗涤过程中既要增加对流场的力，又要保证必要的翻转次数以提高对衣物的清洁效果，在洗涤过程中，洗衣机按照工况三的方式运行。而在洗衣机脱水气液干燥的过程中，为了保证液体流出洗涤筒，在洗涤筒和波轮结合部设计出水口，并且洗衣机按照工况二方式运动，此时可以使波轮静止不动。

3.3.2 洗衣机流场动能

离心式锥形洗衣机通过洗涤筒和波轮的运动带动洗衣机内流体运动，流体的运动不断地冲击衣物，使衣物翻转、摩擦而达到清洁的目的。而流体对于衣物的作用能量来自于流场内部的动能，运动流体动能越大，其对流场中的衣物冲击越剧烈，衣物的洗净效果就越好。因此可以用流场单位质量的平均动能（Mean Kinetic Energy，MKE）来表征整个洗衣机内部流场所具有的动能［13］。

图17是工况三MKE随时间的变化。图中可以看出，平均动能在t＝2 s左右达到最大，此时波轮和洗涤筒在第一个半周期同向转动时间达到最大，流体平均速度达到最大。

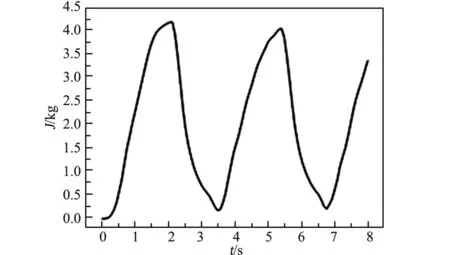
图17 工况三MKE随时间的变化Fig．17 Changes of MKE over time in Case III

流体内部微团之间的碰撞或混合愈剧烈，湍流程度愈大，局部摩擦力也愈大，这样对衣物的清洁效果越好。而湍流的脉动强度可以通过湍流动能（Turbulent Kinetic Energy，TKE）来表征，如式（10）所示：

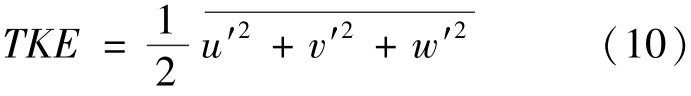
其中，u′、v′、w′是 x、y、z方向速度的脉动量。

图18是工况三单位质量流体TKE随时间的变化。可以得到，在t＝4 s和t＝7 s左右的时候，湍流动能较大，此时流体微团脉动量较大，对衣物的冲击效果更好。从图15、16、17、18工况三条件下洗衣机滚筒、波轮对流场力的作用、流场的MKE与TKE来看，由于滚筒波轮的周期性运动，使这些物理量呈现周期性变化，周期为外部输入周期的一半，T＝3.25 s。

图19是洗衣机在工况三条件下t＝7.2 s时中性截面处的湍动能与速度场分布。可以看出，当t＝7.2 s时，洗衣机内部在靠近滚筒壁的湍动能和速度都最大，衣物受到的冲击最大，洗衣效果也较好。

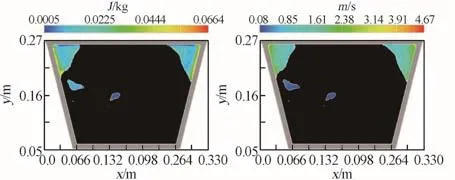
图19 t＝7 #x1001b1; 2 s时工况三湍动能与速度场分布Fig．19 Turbulent energy and velocity magnitude of Case III when t＝7 #x1001b1; 2 s

4 结论

本文基于离心式锥形两相洗衣机的设计方案，针对失重条件下锥形桶内的流体静态分布、筒／波轮旋转时的动态界面形貌和动态流场分布、波轮和洗涤筒对流场力的作用和微重力环境下洗衣机洗净比等关键的微重力流动管理问题开展了研究，得到如下的结论：

1）微重力下锥形筒洗衣机静态流场在表面张力驱动下沿着洗涤筒壁爬升，在气压平衡口处设计楔形气口；

2）洗涤筒的交替旋转使流场产生翻转，而波轮的转动使流场脱离波轮接触；

3）波轮和洗涤筒的同向交替转动对流场的力要大于异向交替转动产生的力，在洗涤过程中的效果更好；

4）在洗涤过程中洗衣机内部流场为湍流，流场能量的耗散使洗衣机平均动能峰值变小；

5）洗衣机在洗涤过程中按照波轮和洗涤筒同向交替运行，脱水过程按照洗涤筒单方向旋转。

（

）

［1］ Victoria B，Noe C，Gary G，et al.Laundry in space：gravity independent laundry system （GILS）［C］ ／／50th AIAA Aero⁃space Sciences Meeting including the New Horizons Forum and Aerospace Exposition， Nashville， Tennessee， 2012：1⁃10.

［2］ 胡文瑞.微重力科学概论［M］.北京：科学出版社，2010： 1⁃12.Hu W R.Introduction to Microgravity Science［M］.Beijing：Science Press， 2010： 1⁃12.（in Chinese）

［3］ Microgravity experiment：wringing a wet towel in space［EB／OL］.http：／／bigthink.com／big⁃think⁃tv／microgravity⁃experi⁃ment⁃wringing⁃a⁃wet⁃towel⁃in⁃space，2013⁃04⁃23.

［4］ Colombo G V， Putnam D F， Lunsford T D， et al.Single phase laundry system development［C］／／23rd International Conference on Environmental Systems， Colorado， 1993：1⁃9.

［ 5 ］ Michalek W， Grounds P.Single⁃phase laundry for long dura⁃tion space missions［C］／／20th International Conference on Environmental Systems， Virginia， 1990： 217⁃222.

［6］ 康琦，侯瑞.微重力流体管理在航天工程中的应用［J］.自然杂志， 2017（06）： 328⁃334.Kang Q， Hou R.Application of microgravity fluid manage⁃ment in aerospace engineering［ J］.Chinese Journal of Na⁃ture， 2017（06）：328⁃334.（in Chinese）

［7］ 张晨辉.微重力下板式表面张力贮箱内流体管理的研究［D］.沈阳：东北大学，2013.Zhang C H.Research on the Liquid Management in the Plate Surface Tension Tank Under Microgravity［D］.Shenyang：Northeast University， 2013.（in Chinese）

［8］ Hirt C W，Nichols B D.Volume of Fluid（VOF）method for the dynamics of free boundaries［J］.Journal of Computational Physics， 1981， 39（1）： 201⁃225.

［9］ Yakhot V，Orzag S A.Renormalization group analysis of tur⁃bulence.I.basic theory［J］.J.Sci.Comput.， 1986， 1（1）：3⁃51.

［10］ William P J，Brain L.The prediction of laminarization with a two⁃equation model of turbulence［J］.Int.J.of Heat Mass Tran， 1972， 15（2）： 301⁃314.

［11］ 刘代祥.波轮式洗衣机的参数设计［J］.家用电器科技，1985（5）： 4⁃7.Liu D X.Parametric design of pulsator type washing machine［J］.Science and Technology of Household Electric Appli⁃ance， 1985（5）： 4⁃7.（in Chinese）

［12］ 龙仲文.对改善波轮式洗衣机结构的初步研究［J］.家用电器科技， 1982（4）： 8⁃12.Long Zhongwen.Preliminary research on improving the struc⁃ture of washing machine ［J］.Science and Technology of Household Electric Appliance， 1982（4）： 8⁃12.（in Chinese）［13］ Mark F，George S，James M.Analysis of cryogenic propellant behavior in microgravity and low thrust environments［J］.Cryogenics， 1992， 32（2）： 230⁃235.