基于故障⁃测试相关模型的运载火箭测试点优化设计方法

周 虎，胡海峰，刘清竹，宋征宇

（1.北京航天自动控制研究所，北京100854；2.宇航智能控制技术国家级重点实验室，北京100854）

1 引言

近年来，随着航天领域产品设计理念的进步，以及对可靠性、维修性、保障性等与测试性相关的重要产品质量特性的理解的不断深入，测试性指标已经成为包括运载火箭在内的装备考核指标的重要组成部分，也成为相关单位进行相关设计、研制、生产的重要依据。同时国际上对测试性设计也日益重视，并针对通用产品测试性设计要求形成了一系列的国际标准，如IEEE标准协调委员会先后制定了IEEE Std 1232《适用于所有环境的人工智能交换和服务标准》［1］、IEEE Std 1641《信号与测试定义标准》［2］等，用于规范通用测试性形式化描述模型与基本框架。测试性是指装备在真实或者模拟环境中，为明确其特征、性能、适用性，或者判断其是否可以有效可靠工作的一类特定内在设计性能［3］。运载箭良好的测试性设计是保证其实现运行故障高测试覆盖率与高准确隔离率的基本前提，也是提高全箭安全性与可靠性指标的重要保障。

通常情况下，运载火箭测试性设计应与系统功能设计同时开展，测试性设计过程中需要考虑两个方面的问题：一是基于总体测试性指标分配方案，设计相应的BIT或者ATE测试方案，保证装备具备规定的测试性能；二是避免引入过度的测试可能大幅度降低运载火箭自身可靠性的情况，也就是说在满足测试性总体要求前提下对测试进行裁剪与压缩，使得能够以较小规模的测试获得装备全面的性能状态指标，即所谓的测试点布局优化问题［4］，即为论文所研究的内容。

国外很早就开展了装备测试性设计相关技术研究。上世纪末，美国康涅狄格大学教授Krishna R.Pattipati和Somnath Deb等人就提出了多信号流图模型，建立了测试与故障间的关系，可用于定量计算对象测试性指标［5］。ARINC公司William R.Simpson等人也提出了信息流模型用于设备故障诊断与隔离［6］。基于上述设计思想，分别出现了QSI公司的TEAMS以及DSI公司的eXpress两类软件，用于装备测试性计算机辅助设计［7］，美国基于TEAMS软件对Ares运载火箭进行了测试性指标分析，并开展了故障诊断领域的尝试工作，取得了一定效果［8］。

随着各类智能搜索算法的不断涌现，科研人员开始尝试将之应用于测试性优化设计领域。如基于AO∗算法对测试集二叉树进行解空间寻优，以提高整体测试效费比［9］；基于粒子群算法，分析大规模集成电路的最优测试途径［10］等。但上述软件与算法多针对装备已经确定的测试点分布现状进行测试流程分析，并不能在产品设计阶段指导测试点布局优化过程［11］。

本文在分析故障与测试内在关联关系的基础上，基于改进的遗传算法，给出一种适用性强的测试点优化布局方法，以在保证满足测试性总体指标的同时最大程度降低装备测试电路规模，达到从根本上提高运载火箭综合测试性能的目的。

2 故障⁃测试相关矩阵

2.1 故障传播特性

考虑系统功能实现与可靠性设计原则，运载火箭通常由多个设备或者基本单元以串联或者并联方式构成。而当其中某个设备或者单元发生故障后，除影响自身性能外，往往还会影响后继设备或者单元的正常运行，即所谓的故障传播特性［12］。一般而言，类似于故障树模型，运载火箭高层级的故障必然由低层级的故障所引发，而低层级的故障可能引发高一层级故障。这类由较低层级逐次向较高层级发展的故障传播模式，称之为纵向故障传播模式；另一方面，某一设备或者基本单元故障通常还会向与之同层级的其他设备或者基本单元扩散，对其他设备或者单元的正常运行造成影响，引发其他故障，称之为横向故障传播模式［13］。

若在运载火箭设备或者基本单元内外部设置了测试点，则这些测试点也能检测到以纵向或者横向模式传播的各类故障。或者说，运载火箭潜在故障模式与测试间存在相关性。

2.2 故障⁃测试相关性分析

一阶相关指对象间存在直接的因果关系。如故障模式f可由测试t直接检测，则称测试t与故障模式f一阶相关。由于测试点一般就近布置于直接被测对象输出端，根据装备FMEA分析结论，很容易地获得所有故障与测试间一阶相关关系。例如在如图1所示的故障传播有向图中，fi（i＝1 ～5）为故障模式，tj（j＝1 ～6）为测试点，则由图可知故障⁃测试对｛f1，t1｝、｛f2，t2｝、｛f2，t3｝、｛f3，t3｝、｛f3，t4｝、｛f4，t5｝、｛f5，t6｝均一阶相关。

图1 故障传播有向图Fig．1 Digraph for fault propagation

全阶相关定义了不同对象间所有直接与间接的因果关系。仍以图1为例，测试t5与故障模式f4一阶相关，同时又与故障模式f2、f1高阶相关，因此测试 t5的全阶相关故障序列为｛f1，f2，f4｝；同理，故障 f2的全阶相关测试序列为｛t2，t3，t5｝。

2.3 全阶相关矩阵

若载人航天运载火箭包含m个可识别的故障，相应地设置了n个测试；其对应的故障传播有向图为 G ＝ ＜V，E ＞，V ＝｛F，T｝ ＝｛f1，f2，… fm，t1，t2，… tn｝为有向图中不加区分的测试或者故障模式节点，其中 F ＝｛f1，f2，……fm｝为系统潜在故障集合，T＝｛t1，t2，… tn｝为可选择的测试集合，则可直接由生成一阶相关矩阵 A＝［aij］（m＋n）×（m＋n），其中元素 aij满足式（1）：

定义与矩阵A对应的全阶相关矩阵D0＝［dij］（m＋n）×（m＋n），该矩阵元素由以下算法确定［14］ ：

1）令矩阵初始值D0＝A；

2）设置行标记 i＝1；

3）对于列标记 j＝1…m ＋n，如果 dij＝1，则将第i行与第j行元素做与操作，即定义k＝1…m＋n，分别令 djk＝djkAND dik；

4）如果 i＜m ＋n，则令 i＝i＋1；返回3），否则结束。

最终生成的D0矩阵可记为式（2）：

根据图论相关知识［15］，FTm×n部分即为故障⁃测试全阶相关矩阵，将之重新命名为矩阵D，记为式（3）：

3 测试性优化布局约束

3.1 测试性指标的定义

基于公式（3）所示的全阶故障⁃测试相关矩阵，可对测试性指标进行描述［16］。定义测试子集TS⊂T，NS≤n为TS的计数，则TS能够检测的故障集合为FD⊂F，应满足式（4）：

其中∪代表逻辑加。令潜在故障集合F对应的故障率λ＝｛λ1，λ2，…，λm｝，可选测试集合 T 对应的测试代价 C ＝｛c1，c2，…，cm｝。 则可定义加权故障检测率FDR（Fault Detection Rate）为能够检测到的故障率与系统总故障率的比值如式（5）：

若Tfi⊂T为可用于检测故障fi的测试集，则fi可被精确隔离，否则fi与fj处于同一模糊组。即应满足式（6）：

其中⊕代表逻辑异或。定义fi的计数Mfi如式（7）：

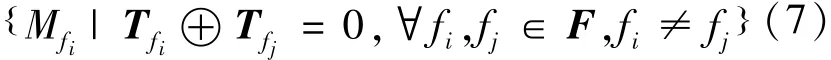
若给定模糊度L≥1，则满足该模糊度下的故障隔离率的故障集合为式（8）：

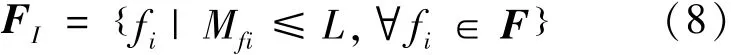
从而可计算加权故障隔离率FIR（Fault Isola⁃tion Rate）如式（9）：

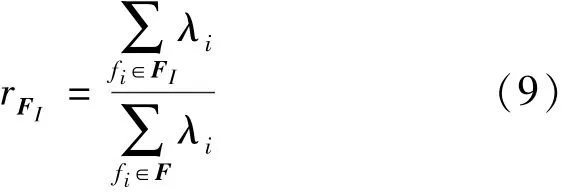
若 ti、tj∈ Ts，i≠ j且测试 ti、tj可测试的故障集分别为 Fti、Ftj⊂ F， 若 Fti＝ Ftj则 ti、tj为冗余测试。

3.2 测试性约束条件

为满足载人航天运载火箭测试性要求，根据相关测试性规范［17］，测试性设计应符合如下条件：

1）故障检测率满足测试性大纲规定的FDR；

2）故障隔离率满足测试性大纲规定的FIR；

3）除有系统专门设计外，要求冗余测试数量为0；

4）在上述约束条件下，尽量使得综合测试效费比最高，综合测试效费包括测试时间、人力成本、测试设备成本等因素。

因此，应在求解得到相关性矩阵基础上，应对测试性参数做如式（10）所示约束，以解得最优测试方案：

其中cj为各项测试成本。

4 运载火箭测试性优化布局求解

4.1 遗传算法

由式（5）、（9）可知，式（10）中约束条件复杂，且各变量间存在较为严重的耦合，使得传统最优化求解算法易陷入局部极值；另一方面，假设载人航天运载火箭可选测试集数量为N，若采用穷举法，则需要对所有可能的测试组合进行遍历操作。由二项式定理，其可用测试组合种类为式（11）：

可用于对不同潜在故障进行检测与隔离的可选测试点数量众多。当N＝100时，K≈1.27×1030；N ＝200 时，K≈1.61 ×1060，N ＝500 时，K≈1.07×10301，理论上使得通过穷举实现载人航天运载火箭测试布局优化成为几乎不可能完成的任务。

遗传算法（Genetic Algorithm，GA）属于一类基于群体搜索策略的最优搜索算法，起源于上世纪60年代对人工自适应系统领域的研究，并于70年代开始在计算机上算法实现［18］。该算法模拟生物基因遗传学基本原理，能够通过群体中多个个体之间的信息交互，以并行计算方式实现群体优化，避免了对梯度的求解；同时算法巧妙地在编码空间而非问题空间进行计算，使得计算过程简单、稳定，容易求得全局极值［19］。遗传算法通常可以分解为如下步骤［20］：

1）初始化染色体种群，一般基于二进制编码或者浮点数编码随机生成L个个体组成的初始种群P，并定义最大进化次数或者期望的目标函数值以控制流程满足终止条件后结束。

2）选择种群个体，根据预定义的适应度函数判断个体优劣，将种群中制定数目的最差评价个体用相同数目的最优个体取代。

3）以一定概率对种群中的多个个体信息重组，进化为下一代种群。

4）种群迭代优化，对择优替换与信息重组两个过程反复迭代，直至性能满足某一指标的群体出现，或者达到最大预设进化次数而得到最优结果。

4.2 测试布局优化的实现

个体比较规则即适应度函数的选择是遗传算法的核心，适应度函数应根据系统测试模型不同而分别建立。定义适应度函数如式（12）：

式中C为采用全部可选测试点时的总测试成本。

传统遗传算法所有个体以等概率参与后续的交叉与变异步骤，易引发局部退化，降低后期收敛速度。本文采用改进后的遗传算法，即考虑到择优选择操作后群体中最优个体存在两份拷贝，可令仅其中一组个体参与后续遗传操作，另一组个体直接传递至下一代种群，从而在保证全局搜索能力的同时提高搜索效率。同时可通过试算法，对适应度函数各项系数λ1、λ2、λ3动态调整，以更加灵活地实现个体比较。

5 数据仿真

为方便起见，以文献［21］中描述的包含18个故障与22个可选测试的复杂系统为例进行算法验证。利用2.3节算法，可得其对应的全阶相关矩阵如表1所示。假设根据系统测试性大纲要求，期望的测试性指标为故障检测率、隔离率均达到为92%以上（隔离模糊组的模糊度为1，即精确隔离故障），无特殊冗余测试要求。

表1 故障⁃测试全阶相关性矩阵Table 1 Fault⁃test full order dependency matrix

采用上述改进后的遗传算法进行整体优化，设定种群规模为50，指定固定的交叉概率0.8，变异概率0.05，采用浮点方式编码，且染色体长度与测试集T长度一致，为22位，染色体允许重复编码（仅计为一次测试）与零编码（该测试位为空），进化代数为100。由于缺乏各潜在故障的故障率信息，可令每一故障的发生几率均相等，每一种测试的平均成本均相当。经试算后，令式（12）中λ1＝ λ2＝ λ3＝1，在Matlab环境下4次仿真计算结果如图2所示。可知每次仿真经过约30次迭代即求解得到最优值，得到的测试序列为 TS＝ ｛t1，t3，t6，t8，t9，t11，t12，t13，t14，t19｝，故障检测率与隔离率分别为94.4%、100%。虽然故障检测率指标下降了5.6%，但仍满足92%以上的规定指标，且经测试点布局优化后，测试点由22个下降到10个，规模缩减了54.5%。测试点的减少意味着相关电路设计的简化，因此对系统可靠性的提高也有很大的效果。

6 结论

利用载人航天运载火箭故障⁃测试间直接相关关系，建立全阶故障⁃测试相关矩阵，并以此为基础，定义可量化的测试性指标和测试布局优化约束条件，进一步利用改进遗传算法对测试布局进行优化设计。从计算、优化过程以及仿真结果来看，该系统方法能够在满足系统测试性要求前提下，快速高效地得到合理的测试性设计结论，可在载人航天运载火箭测试性设计过程中推广使用。

图2 迭代过程Fig．2 Iterative process

（

）

［ 1 ］ IEEE Standards Board.IEEE Std 1232⁃2002 IEEE Standard for Artificial Intelligence Exchange and Service Tie to All Test Environments （AI⁃ESTATE）［S］.Piscataway： IEEE Stand⁃ards Press，2002.

［ 2 ］ IEEE Standards Board.IEEE Std 1641⁃2004.IEEE Standard for Signal and Test Definition［S］.Piscataway： IEEE Stand⁃ards Press，2004.

［3］ 向荫，江丰.装备测试性验证技术综述［J］.电子产品可靠性与环境试验，2016， 34（2）：65⁃70.XIANG Yin，JIANG Feng.A review of testability verification technology of equipment［J］.Electronic Product Reliability and Environmental Testing， 2016，34（2）：65⁃70.（in Chi⁃nese）

［4］ 陈希祥，邱静，刘冠军.装备系统测试性方案优化设计技术研究［J］. 中国机械工程，2010，21（2）：141⁃145.CHEN Xixiang， QIU Jing， LIU Guanjun.Research on tech⁃nologies of optimal testability concept for materiel systems［J］.China Mechanical Engineering， 2010， 21（2）： 141⁃145.（in Chinese）

［5］ Tu F，Pattipati K R，Deb S，et al.Computationally efficient algorithms for multiple fault diagnosis［J］.IEEE Transactions on Systems， Man and Cybernetics， Part B， 2004，34（3）：1490⁃1499.

［6］ Stancic M，Kerknoff H.Testability analysis driven test gener⁃ation of analogue cores［J］.Microelectronics Journal， 2003，34（10）：913⁃917.

［7］ Liu D，Zeng Z，Huang C，et al.The testability modeling and model conversion technology based on multi⁃signal flow graph［C］ ／／Proceedings of the IEEE Conference on Prognostics and System Health Management（PHM）， Beijing， P.R.China，2012.

［8］ 宋征宇.新一代运载火箭的数据驱动快速测试技术［J］.宇航学报， 2015， 36（12）： 1435⁃1443.SONG Zhengyu.Data⁃driven responsive test technique for new generation launch vehicle［J］.Journal of Astronautics， 2015，36（12）： 1435⁃1443.（in Chinese）

［9］ Shakeri M，Raghavan V，Pattipati K R.Sequential testing al⁃gorithms for multiple fault diagnosis［J］.IEEE Trans.on SMC， 2000，30（1）：1⁃14.

［10］ 蒋荣华，王厚军，龙兵.基于DPSO的改进AO∗算法在大型复杂电子系统最优序贯测试中的应用［J］.计算机学报， 2008， 31（10）： 1835⁃1840.JIANG Ronghua， WANG Houjun， LONG Bing.Applying im⁃proved AO∗based on DPSO algorithm in the optimal test⁃se⁃quencing problem of large⁃scale complicated electronic system［J］.Chinese Journal of Computers， 2008， 31（10）： 1835⁃1840.（in Chinese）

［11］ ZHOU Hu， LI Haimeng， QI Guangping， et al.Design for testability analysis and test plan optimization for launch vehi⁃cle［C］ ／／2016 IEEE Chinese Guidance， Navigation and Con⁃trol Conference， Nanjing， P.R.China， 2012.

［12］ 连光耀，黄考利，吕晓明，等.基于混合诊断的测试性建模与分析［J］.计算机测量与控制，2008，16（5）：601⁃603.Lian Guangyao， Huang Kaoli， Lv Xiaoming， et al.Analyzing and modeling of testability based on hybrid diagnostic［J］.Computer Measurement＆ Control， 2008， 16（5）： 601⁃603.（in Chinese）

［13］ 王成刚，周晓东，彭顺堂，等.一种基于多信号模型的测试性评价方法［J］. 测控技术，2016（1）： 13⁃15.WANG Chenggang， ZHOU Xiaodong， PENG Shuntang， et al.Testability evaluation based on multi⁃signal modeling methodology［J］.Measurement＆ Control Technology， 2016（1）： 13⁃15.（in Chinese）

［14］ 叶红.可达矩阵的Warshall算法实现［J］.安徽大学学报（自然科学版）， 2011， 35（4）： 31⁃35.YE Hong.Reachability matrix by Warshall algorithm［J］.Journal of Anhui University （Natural Science Edition），2011， 35（4）： 31⁃35.（in Chinese）

［15］ 杨鹏.基于相关性模型的诊断策略优化设计技术［D］.长沙：国防科学技术大学，2008.Yang Peng.Optimal Design Technique of Diagnostic Strategy based on Correlation Model［D］.Changsha， China： National University of Defense Technology， 2008.（in Chinese）

［16］ 王宝龙，黄考利，马立元，等.基于依赖矩阵的测试性分析［J］. 计算机测量与控制， 2011.19（6）：1260⁃1265.Wang Baolong， Huang Kaoli， Ma Liyuan， et al.Dependency matrix based testability analysis［J］.Computer Measurement＆ Control， 2011， 19（6）： 1260⁃1265.（in Chinese）

［17］ 总装备部.GJB 2547A装备测试性工作通用要求［S］.北京：总装备部军用标准出版发行部，2012.General Armament Department.GJB 2547A General Require⁃ments for Material Testability Program［S］.Beijing： Military standard publication and Distribution Department of General Armament Department， 2012.（in Chinese）

［18］ 马永杰，云文霞.遗传算法研究进展［J］.计算机应用研究， 2012， 29（4）： 1201⁃1206.MA Yongjie， YUN Wenxia.Research progress of genetic al⁃gorithm［J］.Application Research of Computers， 2012， 29（4）： 1201⁃1206.（in Chinese）

［19］ 刘刚，黎放，胡斌.基于改进遗传算法的测试性优化分配方法［J］. 火力与指挥控制，2014，39（1）： 44⁃47.LIU Gang， LI Fang， Hu Bin.Research on testability optimi⁃zation allocation method based on improved genetic algorithm［J］.Fire Control＆ Command Control， 2014， 39（1）： 44⁃47.（in Chinese）

［20］ 李元新，吴斌.基于遗传算法的测试资源优化分配方法研究［J］. 飞行器测控学报，2005，24（4）： 1⁃5.LI Yuan⁃xin， Wu Bin.GA⁃based optimal allocation of station resources［ J］.Journal of Spacecraft TT＆C Technology，2005， 24（4）： 1⁃5.（in Chinese）

［21］ 丁昊.基于多信号流图的系统测试性建模分析及软件设计［D］.哈尔滨：哈尔滨工业大学，2013.Ding Hao.Modeling，Analysis and Software Design for System Testability based on Multi⁃signal Flow Graph［ D］.Harbin：Harbin Institute of Technology， 2013.（in Chinese）