交指状电极结构仿真分析及其电场分布拟合

刘亚永， 李尧生， 徐鲁宁， 韩 立

(1. 中国科学院电工研究所， 北京 100190； 2. 中国科学院大学， 北京 100049;3. 电力设备电气绝缘国家重点实验室， 西安交通大学， 陕西 西安 710049)

1 引言

阻尼器是虚拟现实、摇操作、触觉显示以及吸能减振、缓冲冲击等领域的重要部件[1-3]。现有的阻尼器参数固定、不可调；而电流变阻尼器采用基于电流变液(ElectroRheological Fluids，ERF)的智能材料，由于其屈服应力可由外加电场调节的特性，使得其阻尼响应可以实现动态可调。现有的电流变阻尼器由于采用平板式电极结构，负载工作时的最高剪切速率较低，难以满足虚拟现实及缓冲冲击等负载运动速率较高领域的应用需求，因此需要进一步提高电流变阻尼器的这项指标[4-6]。

交指状电极结构(interdigital electrodes configuration)改变了电场分布形态，与只能提供与剪切方向相垂直的电场的传统平板电极相比，增加了与电流变液剪切方向相平行的电场分量，能够有效地提高电流变阻尼器工作时的最高剪切速率[6,7]。然而，交指状电极结构的几何尺寸(电极宽度、绝缘宽度)对其电场平行分量的影响规律尚不清楚，无法将交指状电极结构有效地应用于电流变阻尼器的设计。

电流变液是由微、纳米尺度的介电颗粒与绝缘液体按一定比例混合而成的复杂流体，当施加电场时，分散相颗粒极化后相互吸引，形成链柱状结构，使得电流变液体系中的粘度迅速增加，具有一定的屈服应力，响应时间为毫秒级，且过程连续可逆。这些特性，使其成为智能阻尼器的理想介质[8-11]。

本文依据交指状电极结构的实验平台、电磁场理论及有限元方法，建立了交指状电极结构在静电场作用下的有限元模型，并对该模型做合理的简化处理。在此基础上，采用有限元软件COMSOL Multiphysics 5.2a仿真分析交指状电极结构的几何尺寸与电场平行分量的关系。为了更好地将仿真结果应用于基于交指状电极结构的电流变阻尼器的设计，以及对其实现智能控制，采用Matlab软件拟合仿真数据，得到交指状电极结构的几何尺寸对其电场平行分量影响规律的数学表达式，并验证了该表达式的可靠性。

2 仿真分析方法

2.1 仿真模型

本研究建立的交指状电极的仿真模型以实验测试台架为基础。将Brookfield R/S流变仪的金属底座换成同尺寸的交指状电极底座，并将交指状电极底座与金属转子做相应的绝缘处理，以免施加的高电压损坏仪器。具体结构如图1所示。从下至上依次为：金属底座、绝缘层1(包括FR-4环氧板、ABS塑料两层)、交指状电极、绝缘层2(尼龙)、金属转子。研究区域为绝缘层2的下表面与交指装电极的上表面之间的空间，这是电流变液的有效工作区域。

图1 仿真模型Fig.1 Model of simulation

金属转子有两种规格：①直径75mm，厚度1.5mm，用于屈服应力较小的电流变液的测量；②直径25mm，厚度1.5mm，用于屈服应力较大的电流变液的测量。绝缘层2有直径75mm、25mm两种规格，厚度均为2mm，分别与金属转子相配套。交指状电极高度为0.02mm，附着于绝缘层1表面；交指状电极的上表面与绝缘层2的下表面的间距为0.2mm，为板间间距；交指状电极宽度的变化范围为0～1mm，正、负电极间距的变化范围为0～1mm；绝缘层1中FR-4的厚度为1.6mm，ABS的厚度为8.4mm；金属底座约为10mm。金属转子与金属底座接地连接；工作时，交指状电极之间施加稳定的电势差。

2.2 交指状电极在静电场中的有限元模型

交指状电极的静电场求解问题一般可归结于偏微分方程的边值问题。根据静电学中汤姆逊定理，即处于介质中的一个固定的带电导体系统，其表面上电荷的分布，应使合成的静电场具有最小的静电能量，其表达式为：

(1)

找出能量泛函的积分式，并令其在满足狄氏边界条件的前提下取极值，即构成与偏微分方程边值问题等价的条件变分问题，即

(2)

式中，J[φ(x,y)]为能量的泛函。

交指状电极在静电场作用下的有限元模型一般按剖分场域、选取插值函数、泛函离散化、边界条件的处理等步骤建立。经过上述步骤后，所研究区域和对象被划分为N个单元、n个节点的有限元模型，式(2)的条件变分问题将离散化为一个多元函数的极值问题，从而导出一组联立的代数方程，即有限元方程：

(3)

式中，K为n×n阶系数矩阵；φ0为节点的初始电势值；f为n×1阶激励矩阵。式(3)表示求解区域内未知电势函数值与求解域的边界条件以及激励源的关系，常称为整体矩阵方程。求解式(3)，可得区域内电势的数值解[12-14]。

3 交指状电极在静电场中的仿真分析

简单的静电场模型可按2.2节的步骤进行建模和分析，而对于本文这种较为复杂的静电场分析问题，采用大型电磁场分析软件进行计算、辅助分析，更利于将研究重点放在交指状电场结构参数对静电场平行分量的影响规律上。本文利用有限元分析软件COMSOL Multiphysics 5.2a建立交指状电极在静电场作用下的有限元模型，并进行仿真计算。在建模过程中为了便于分析，减少计算量，作如下简化：

(1)电极长度远远大于电极宽度，可视为无限延伸，将模型从三维简化为二维。

(2)因为模型中的交指状电极结构是按正极、绝缘、负极、绝缘这样的周期性多次延伸下去，可视为无限延伸，所以采用周期性边界条件。

(3)模型中认为金属转子和金属底座是理想导体且接地，即等势体；正、负电极间存在稳定电势差。

图2为简化后的仿真模型单元。其中，w为电极宽度，变化范围为0～1mm；l为电极与电极之间的绝缘宽度，变化范围为0～1mm；b为电极高度，为0.02mm；δ为绝缘层2到电极上表面的间距，为0.2mm，即为板间间距；a为仿真模型单元的宽度，即交指状电极结构的循环周期长度[15-17]。

图2 仿真模型单元Fig.2 Model unit of simulation

3.1 边界条件

图3为仿真模型单元的边界条件。图3(a)为狄氏边界条件1，其中粗线边界是高压电源的正极所加的边界，变化范围为0～5000V，在电场强度一定的情况下，其值取决于电极与电极之间的绝缘宽度，此处为1000V；图3(b)为狄氏边界条件2，其中粗线边界是电位值为零的边界；图3(c)中，粗线是周期性边界条件，交指状电极按正极、绝缘、负极、绝缘这样的周期性无限延伸下去。

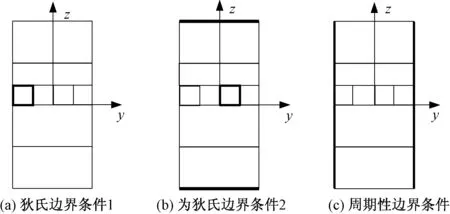
图3 仿真模型单元的边界条件Fig.3 Boundary conditions of simulation model unit

3.2 仿真结果与讨论

3.2.1 电势分布

在电极宽度及绝缘宽度都为1mm的情况下，仿真模型单元区域中的电势分布如图4所示。从图4可知，电势由正电极分别向零电位衰减，由于不同介质的相对介电常数不同，电势分布的高度曲面在不同介质的过渡区域出现了略微的波动，这与实际电势分布比较吻合。电势的分布与本文实际测量值基本一致，说明仿真结果是正确的。

图4 仿真模型单元区域内电势分布Fig.4 Electrical potential distribution of model unit

3.2.2 电场平行分量绝对值的分布

电极宽度及绝缘宽度都为1mm的情况下，仿真模型单元区域内电场平行分量绝对值分布如图5所示。其中，箭头方向为平行分量的方向，线段长度代表取对数后的平行分量的大小；白色区域表示电场平行分量的绝对值大于106V/m的区域，其主要分布在电极端点附近，这主要是因为在电极的端点电场发生了畸变。从图5可以看出，电场平行分量主要集中在电极附近，尤其是电极之间的空气间隙区域中，而且随着距离电极距离的增加，衰减很快。

图5 仿真模型单元区域内电场平行分量绝对值分布Fig.5 Distribution of absolute value of parallel components of electric field in model unit

3.2.3 仿真模型单元中研究区域内电场平行分量的绝对平均值分布

电场平行分量的绝对平均值A的表达式为：

(4)

式中，es.Ex为仿真模型单元中研究区域内某一点的电场平行分量值。仿真模型单元中研究区域内电场平行分量的绝对平均值随绝缘宽度及电极宽度变化的分布如图6所示，其中l表示交指状电极的绝缘宽度。

图6 模型单元中研究区域内电场平行分量的绝对平均值分布Fig.6 Distribution of absolute value of parallel components of electric field in air zone of model unit

由图6可知，在绝缘宽度一定的情况下，仿真模型单元中研究区域内电场平行分量的绝对平均值随电极宽度的增加呈单调递减的趋势，且这种趋势随着绝缘宽度的增加，逐渐变缓；在电极宽度一定的情况下，交指状电场平行分量的绝对平均值随绝缘宽度的增加呈单调增加的趋势，且这种趋势随着绝缘宽度的增加不断减小。综上所述，电极宽度越小，绝缘宽度越大，仿真模型单元中研究区域内电场平行分量的绝对平均值越大。

3.3 对仿真模型单元中研究区域内电场强度平行分量绝对平均值分布的拟合

基于Matlab的拟合评价标准及对各种拟合模型的对比，本文选择基于多项式的拟合模型，对仿真数据进行拟合。拟合表达式如式(5)所示，置信水平为95%的多项式拟合系数及其置信区间如表1所示。

(5)

考察拟合优劣的主要指标有三个方面：①拟合优度(goodness of fit)；②残差分析；③置信水平与置信区间[18-20]。下面将结合这三个方面的评价指标对拟合曲面进行分析。

表1 拟合方程系数及其置信区间(置信水平95%)Tab.1 Equation coefficient of fitting and its confidence interval (with 95% confidence level)

3.3.1 拟合优度

电场强度平行分量绝对平均值随交指状电极的电极宽度和绝缘宽度分布的曲面拟合优度如表2所示。

表2 电场强度平行分量绝对平均值分布的曲面拟合优度Tab.2 Goodness of fit of distribution of absolute mean value of parallel component of electric field intensity

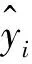
(6)

式中，wi为权重因数。SSE越接近于0，说明模型选择和拟合更好，数据预测也越成功。

RMSE为均方根，该统计参数是拟合数据和原始数据对应点误差的平方和的均值，即RMSE=SSE/n，其中n为残差自由度。与SSE类似，RMSE越接近于0，说明模型选择和拟合更好，数据预测也越成功。

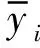
(7)

(8)

R-square通过数据的变化来表征一个拟合的好坏。由式(6)～式(8)可知，R-square的正常取值范围为[0，1]，越接近1，表明方程的变量对y的解释能力越强，该模型对数据拟合得越好。AdjustedR-square为自由度修饰后的R-square，其值小于等于1，越接近1，表明方程的变量对y的解释能力越强，该模型对数据拟合得越好，负值表示模型中含有无关变量。

从表2可以看出，拟合优度数值比较理想。

3.3.2 残差分析

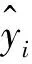
(9)

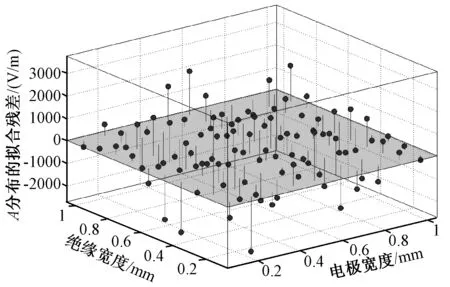
图7 电场强度平行分量绝对平均值分布的拟合残差图Fig.7 Fitting residual map of absolute mean distribution of parallel components of electric field

如果拟合模型正确，Residuals呈随机分布；Residuals分布得越随机，表明模型对数据拟合得越好。在原始100个数据点中，残差大于0的有45个，小于0的有50个，等于0的有5个；残差并没有集中于某个区域。另外，由图7可知，残差为正、为负、为零的点出现得比较随机，没有明显的规律性、趋势性，拟合残差呈随机分布。

3.3.3 置信水平与预测区间

图8为交指状电极电场强度平行分量绝对平均值随其电极宽度和绝缘宽度分布的拟合曲面，及其置信水平为95%条件下的预测区间。由表1可知，拟合方程系数置信区间比较窄，说明预测区域的变动范围也比较窄，即该曲面对原始数据的拟合比较准确，拟合结果有意义。

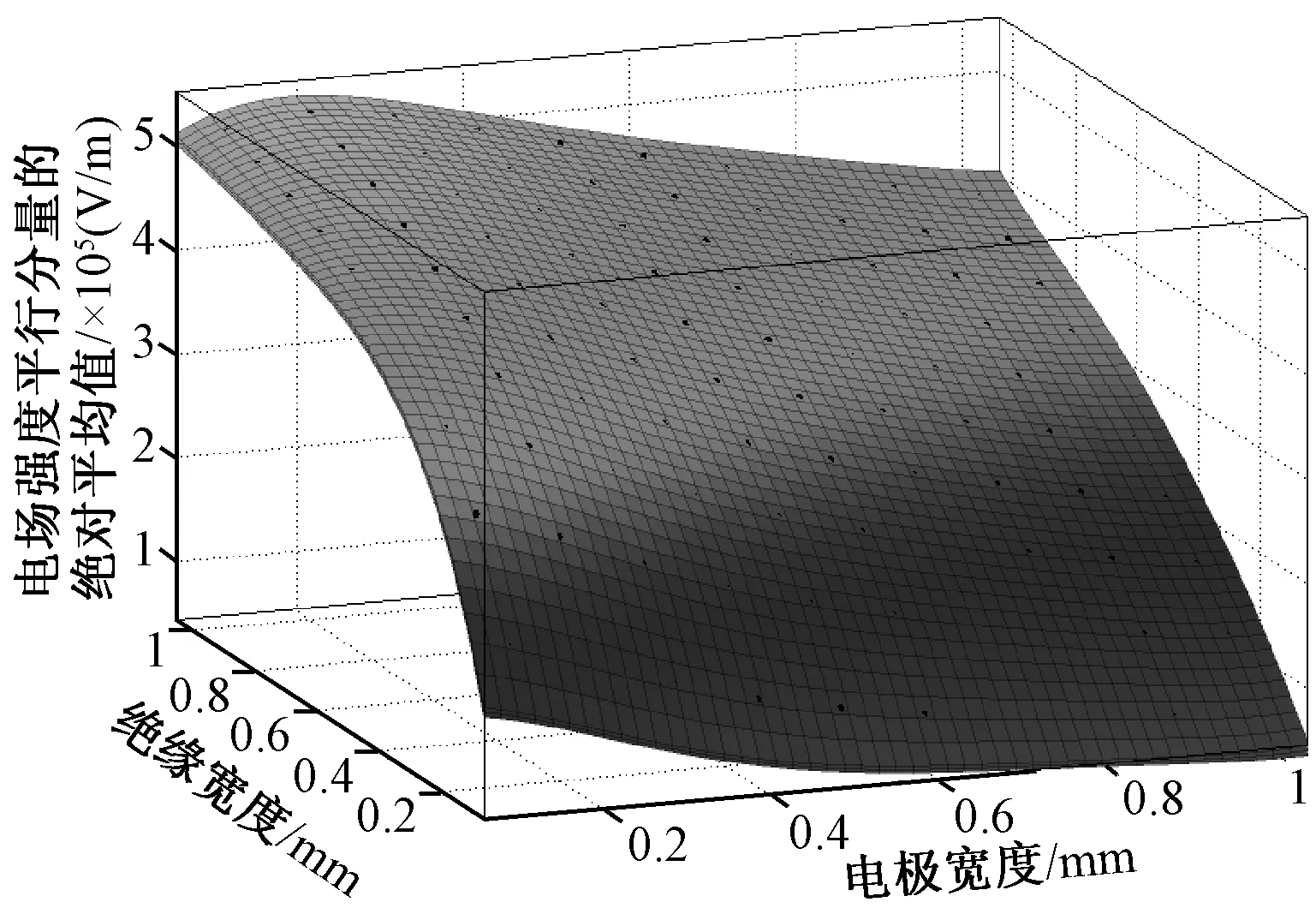
图8 电场强度平行分量绝对平均值分布的拟合曲面Fig.8 Fitting curve of distribution of absolute mean value of parallel components of electric field intensity

对拟合优度、残差分析、置信水平与预测区间三个方面的讨论分析表明，选用5次多项式拟合交指状电场平行分量的分布曲面能够真实反映拟合原始数据。

4 结论

本文采用仿真分析方法，研究了交指状电极结构的几何参数对其电场平行分量的影响规律。仿真结果表明，电极宽度越小，绝缘宽度越大，仿真模型单元中研究区域内电场平行分量的绝对平均值越大。

将交指状电极结构在不同几何尺寸下空间电场平行分量的分布规律进行了曲面拟合，得出交指状电极结构电场分布的控制方程。经过对其拟合优度、残差及置信水平与置信区间三种评价指标的分析，表明5次多项式的曲面表达式能准确地反映交指状电极结构的几何参数对其电场平行分量的影响规律，可用于基于交指状电极结构的电流变阻尼器的设计。

[1] Bose H, Berkemeier H J. Haptic device working with an electrorheological fluid[J]. Journal of Intelligent Material Systems and Structures, 1999, 10(9): 714-717.

[2] Mavroidis C, Pfeiffer C, Celestino J, et al. Controlled compliance haptic interface using electro-rheological fluids[A]. Smart Structures and Materials 2000: Electroactive Polymer Actuators and Devices [C]. Bellingham, USA, 2000. 3987:300-310.

[3] Sakaguchi M, Furusho J, Takesue N. Passive force display using ER brakes and its control experiments[A]. Proceedings IEEE Virtual Reality 2001 [C]. Yokohama, Japan, 2001. 7-12.

[4] Tian Y, Meng Y, Mao H, et al. Electrorheological fluid under elongation, compression, and shearing[J]. Physical Review E, 2002, 65(3): 031507.

[5] 尹剑波，赵晓鹏(Yin Jianbo, Zhao Xiaopeng). 电场调控的智能软材料(Smart soft materials tuned by electric fields)[M]. 北京：科学出版社(Beijing: Science Press)，2010.

[6] Liu Liyu, Huang Xixiang, Shen Cai, et al. Parallel-field electrorheological clutch: Enhanced high shear rate performance[J]. Applied Physics Letters, 2005, 87(10): 104106.

[7] Sheng Ping, Wen Weijia. Electrorheology: Statics and dynamics[J]. Solid State Communications, 2010, 150(21-22): 1023-1039.

[8] Halsey T C. Electrorheological fluids[J]. Science, 1992, 258(5083): 761-766.

[9] 赵晓鹏，罗春荣，周本濂(Zhao Xiaopeng, Luo Chunrong, Zhou Benlian).ER流体特性及其研究现状(Characteristics of ER fluids and its current status)[J].材料科学与工程(Materials Science and Engineering)，1993，11(4): 1-6.

[10] Winslow W M. Induced fibration of suspensions[J]. Journal of Applied Physics, 1949, 20(12): 1137-1140.

[11] 赵晓鹏，罗春荣，周本濂(Zhao Xiaopeng, Luo Chunrong, Zhou Benlian). ER流体的应用前景展望(Application prospect of ER fluid)[J].材料导报(Materials Review)，1993, (6): 12-15.

[12] 倪光正，杨仕友，邱捷(Ni Guangzheng, Yang Shiyou, Qiu Jie). 工程电磁场数值分析(Numerical analysis of engineering electromagnetic field)[M].北京：机械工业出版社(Beijing: China Machine Press)，2009.

[13] 倪光正(Ni Guangzheng). 工程电磁场原理(Principle of engineering electromagnetic field)[M].北京: 高等教育出版社(Beijing: Higher Education Press)，2009.

[14] Ida N. Engineering Electromagnetics [M]. New York: Springer，2000.

[15] 马中原，廖承林，王丽芳(Ma Zhongyuan, Liao Chenglin, Wang Lifang). 金属异物对电动汽车无线充电系统影响分析(Analysis of metal foreign object setting on electric vehicle wireless power transfer system)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2017, 36(2): 14-20.

[16] 郭凤仪，刘帅，王智勇(Guo Fengyi, Liu Shuai, Wang Zhiyong). 弓网系统滑动电接触瞬态温度场仿真研究(Research on transient temperature field of electrical sliding contact in pantograph and catenary system)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2017, 36(3): 29-34.

[17] 李丹，徐蓉，袁伟群，等(Li Dan, Xu Rong, Yuan Weiqun, et al.). 电磁发射装置绝缘支撑结构多场特性研究(Study on multi-physics characteristics of insulators in electromagnetic launcher system)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2016, 35(8): 36-39.

[18] 盛骤，谢式千，潘承毅(Sheng Zhou, Xie Shiqian, Pan Chengyi). 概率论与数理统计(Probability theory and mathematical statistics) [M]. 北京：高等教育出版社(Beijing: Higher Education Press)，2009.

[19]Dexter F, Ledolter J. Bayesian prediction bounds and comparisons of operating room times even for procedures with few or no historic data[J]. Anesthesiology, 2005, 103(6): 1259-1267.

[20]Zhou J S, Dexter F. Method to assist in the scheduling of add-on surgical cases - Upper prediction bounds for surgical case durations based on the log-normal distribution[J]. Anesthesiology, 1998, 89(5):1228-1232.