求解电力系统多目标环境经济调度的帕累托最优MFO算法
2018-03-21杨德友刘世宇
杨德友, 刘世宇
(东北电力大学电气工程学院, 吉林省 吉林市 132012)
1 引言
化石能源(煤炭、石油、天然气等)的日益匮乏及温室效应的突显,使得在化石能源高效利用的同时需考虑其污染物排放问题,建立环境友好型的化石能源利用形式是能源行业的核心任务之一。
火力发电厂通过燃烧化石燃料将化学能转化为电能,是化石能源消耗的主体,也是污染气体重要源头之一。“十三五”期间中国将加大环境综合治理力度,大力推进污染物达标排放和总量减排。因此,电力系统发电厂有功调度过程中不仅要考虑经济性[1],同时必须兼顾污染物排放问题,将污染物排放指标引入电力系统有功调度中,构建同时考虑经济性和污染物排放两个指标的目标函数,即电力系统环境经济调度(Economic-Environmental Dispatch,EED)。
EED求解过程中需要同时使经济指标和污染物排放指标达到最小,这是典型的多目标优化问题[2,3]。目前,多目标优化问题的全局最优解的求取依然十分困难,为此国内外专家学者针对多目标EED问题开展了广泛的研究。文献[4]提出了基于回溯搜索算法(Backtracking Search Algorithm,BSA)的EED求解方法,该方法通过对BSA算法本身敏感的控制参数的改变求解EED问题。文献[5]采用改进细菌觅食算法(Modified Bacterial Foraging Algorithm,MBFA),通过合理改变参数整定对EED 问题进行了模拟,但BSA和MBFA算法的参数设置和算法实现过程过于复杂。文献[6]通过给单目标函数匹配不同权值,实现了多目标到单目标的转化,提出了基于生物地理学算法(Biogeography-Based Optimization,BBO)的EED求解方法,并进行了数值模拟。文献[7]通过设置罚因子将废气排放目标嵌入到发电机煤耗费用目标中,将多目标规划问题转化为单目标规划问题,并利用花朵授粉算法(Flower Pollination Algorithm,FPA)进行求解。文献[8]运用粗糙集理论确定环境调度和经济调度函数的约束度,进而确定多目标权系数,运用混沌局部搜索策略的差分进化算法 (Chaotic Local Search strategy Differential Evolution,CLSDE)对EED问题进行求解。但权系数法中各个目标函数需要在求解前进行认知赋值,权重系数直接影响优化结果,自适应性较差。文献[9]通过对罚系数值的设定,将污染排放目标同总燃料费用目标结合起来,将多目标规划问题转化为单目标问题,并分别利用调制粒子群优化算法(Modulated Particle Swarm Optimization,MPSO)和改进量子粒子群算法(Improved Quantum Particle Swarm Optimization,IQPSO)获取单目标最优解,进而实现了EED的求解,但对罚系数值的设定并不能满足多目标优化需求。
飞蛾扑火算法(Moth-Flame Optimization algorithm,MFO)是Seyedali Mirjalili于2015年提出的模拟飞蛾扑火行为的进化算法[10],具有收敛性强、收敛速度快、适用范围广等优点,在求解高维优化问题时,其优势更为明显。本文选择MFO作为基础优化算法,结合帕累托最优策略,提出了基于帕累托最优与MFO算法的多目标EED求解方法。通过与现有优化算法结果的对比与分析,验证了本文算法的可行性和有效性。
2 基于帕累托最优的EED模型
EED问题需要在满足用户用电需求、系统网络损耗、火电厂各发电机组有功出力参数设计等约束条件下,对系统中各个发电机组的有功分配进行优化,尽可能使总燃料成本和总污染排放量最小。
2.1 基本EED模型
(1)总燃料成本
火电厂中每台发电机的发电成本之和即为总燃料成本F(Pi),它可被近似表示为:
(1)
式中,Pi为第i台发电机的有功出力;N为发电机的数量;ai、bi、ci为第i台发电机的煤耗特性系数。
在实际系统中,发电机组能耗曲线需要由汽轮机汽门来调节,从而改变发电机组的有功出力。在此过程中会产生一定的能耗损失,称为阀点效应,可以表示为:
Di=disin[fi(Pimin-Pi)]
(2)
式中,Di为阀点效应所引起总燃料成本的变化量;Pimin为第i台发电机有功出力的下限;di、fi为发电机组的阀点系数。
因此,实际发电机组的总燃料成本可表示为:
(3)
(2)总污染排放量
由于国家对火力发电厂污染气体排放,如SO2、NOX等有明文规定,要求其控制污染气体的排放量。本文仅考虑NOX气体的排放情况,因此总污染排放量E(Pi)可表示为:
(4)
式中,αi、βi、γi、ηi、δi为第i台发电机的排放特性系数。
2.2 约束条件
由于系统安全和发电机组自身运行特性的限制,在调度过程中应首先考虑平衡约束和容量约束。平衡约束条件可以表示为:
(5)
式中,PD为系统负荷;PL为系统网络损耗,可以利用Kron公式[11]进行计算,其公式如下:
(6)
式中,Bij、B0i、B00为网络参数。
机组发电容量自身同样受到出力上下限约束,可表示为:
Pimin≤Pi≤Pimax
(7)
式中,Pimax为第i台发电机有功出力的上限。
综合上述约束,EED问题的多目标优化模型可以表示为:
(8)
式中,F(Pi)和E(Pi)分别为煤耗费用和污染气体排放量目标函数;g(Pi)为系统的等式约束条件;h(Pi)为系统的不等式约束条件。
2.3 基于帕累托最优的EED求解模型
帕累托最优[12]表征了多目标不能同时满足所有目标同时继续优化的一种平衡状态。帕累托最优可以使多目标在寻优过程中达到单目标适应度的合理最优配置。
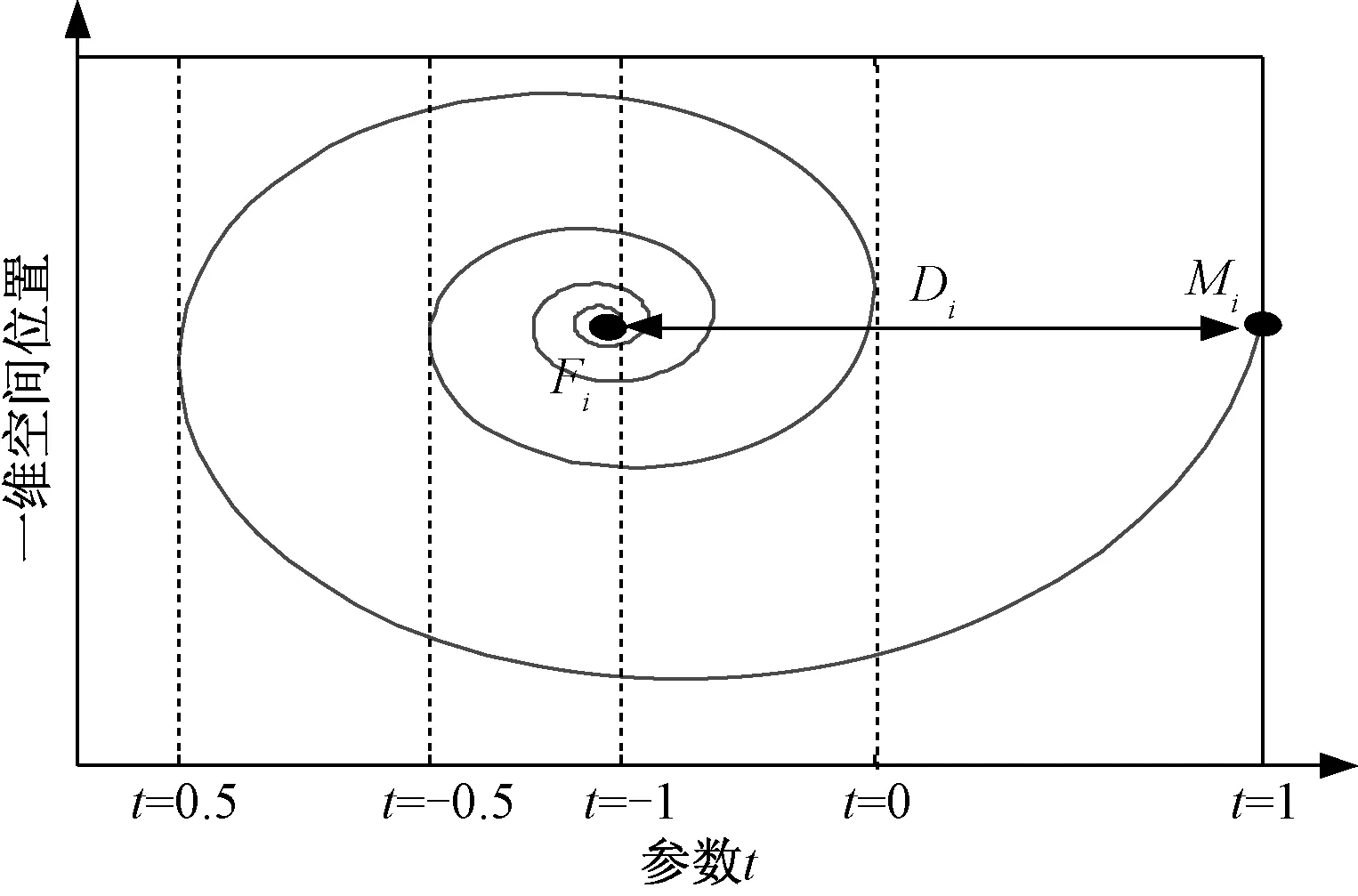
设X为EED问题的解集,式(8)中若∀i∈{1,2,…,n}均满足fi(α)< EED问题需要同时考虑煤耗费用和污染气体排放量。该问题是一种向量化综合优化配置问题,最优方案的求取取决于目标向量的更新和比较。 帕累托非劣性解向量分布的均匀程度可由间隔指标S[13]来衡量: (9) 式中 m为目标函数中目标个数;n为非劣性解集中解向量个数。当S=0时表示该非劣性解集呈均匀分布。 此时所得全部非劣最优解构成了多目标优化问题解的帕累托最优前沿,通过对前沿中的方案进行排序,即在可行域中搜索出最优的调度方案。 在MFO算法中,假设飞蛾是候选解,问题的变量是飞蛾在空间中的位置,飞蛾的位置矩阵可以表示为: (10) 式中,n为飞蛾数量;d为变量个数(维数)。 对于所有飞蛾,假设存在一个可以存储适应值的向量: (11) 这里的适应值是每只飞蛾适应值函数的返回值。每只飞蛾的位置向量(例如矩阵M的第一行)被传递给了适应值函数,适应值函数的输出值即为对应飞蛾的适应值(例如OM矩阵中的OM1)。 MFO算法的另一个重要组成部分是火焰。其位置矩阵可以表示为: (12) 事实上,矩阵M和F具有相同的维数。对于火焰,假设存在一个可以储存对应适应值的向量: (13) MFO算法是一种求解非线性规划问题的全局最优解的三维方法,可以定义为: MFO=(I,P,T) (14) 式中,I为一种可以产生随机飞蛾和对应适应值的函数,I函数的数学模型可以表示为: I:φ→{M,OM} (15) P函数为主函数,可以在搜索空间里自由移动飞蛾的位置,P函数通过矩阵M的更新来记录飞蛾的最终位置,即 P:M→M (16) T函数为终止函数,当T函数满足终止条件时,则函数将返回真,此时停止运行;否则返回假,P函数将继续进行搜索,即 T:M→{真,假} (17) I函数可以产生最初解,并且计算出目标函数值。I函数可以利用任何随机分布进行计算,MFO算法中飞蛾的随机分布可以表示为: M(i,j)=(ubi-lbi)·rand()+lbi (18) 式中,ub和lb为随机分布过程中存在的向量,这两个向量规定了变量的最大值和最小值,即 ub=[ub1,ub2,…,ubi,…,ubn] (19) 其中,ubi为第i个变量的最大值。 lb=[lb1,lb2,…,lbi,…,lbn] (20) 其中,lbi为第i个变量的最小值。 初始化后,P函数将会进行反复迭代,直到T函数返回为真时停止计算。本文算法中,飞蛾的更新过程是一种对数的螺旋关系。在搜索过程中,螺旋范围的波动不可以超出搜索区间。因此,该算法对数螺旋可以定义为: S(Mi,Fj)=Diebtcos(2πt)+Fj (21) 式中,Di为第i只飞蛾和第j个火焰之间的距离;b为可以改变对数螺旋形状的常数;t为在[-1,1]之间的随机数。 D的计算方法如下: Di=Fj-Mi (22) 式中,Mi表示第i只飞蛾;Fj表示第j个火焰。 对于上述模型可以描述为: (1)飞蛾可以通过改变t值收敛到火焰周围的任何点。 (2)t值越小,距离火焰就越近(如图1所示)。 图1 根据t值改变飞蛾在火焰周围的螺旋位置Fig.1 Changing position of moth around flame according to t value (3)火焰周围的飞蛾频繁更新位置可以增加飞蛾接近火焰的概率。 飞蛾位置的更新可以保证飞蛾始终在火焰周围进行搜索。在优化过程中,飞蛾将根据矩阵更新位置。假设存在一个在区间[r,1]的随机数t,其中r为收敛常数,是一个在迭代过程中由-1~-2线性递减的变量。 在每次迭代中,火焰会根据适应值分类。在更新过程中,若所有飞蛾均被相同火焰吸引,则飞蛾将在搜索空间内收敛到同一个点。同时,飞蛾位置更新可能出现在不同的火焰周围,这种机制使飞蛾在搜索区域突然移动,这也提升了探测进程。 然而,飞蛾位置在搜索区域内进行n次不同的位置更新可能会降低对最优解的探测。这样可以使火焰数量在迭代过程中逐渐减少,火焰数量flameno可表示为: (23) 式中,l为当前迭代次数;N为最大火焰数量;T为最大迭代次数。 迭代过程后期,飞蛾只在最优火焰处更新位置,在搜索区域定位和探测,并且使火焰数量逐渐下降。此时,当T函数返回真时,P函数停止。本文引入算法基本流程图如图2所示。 图2 MFO算法流程图Fig.2 Flow chart of MFO algorithm EED问题为多目标优化问题,通过对帕累托策略的引入可以将本文算法适用于多目标MFO优化求解,在此过程中引入累计排序适应度赋值策略、精英保留策略和拥挤距离计算策略[14]。 具体经济节能调度基本步骤如下: (1)设置求解EED问题所用算法基本参数(系统负荷总量、发电机组煤耗特性参数、污染排放参数等)。 (2)利用计算方法内部初始化函数对搜索粒子进行初始位置确定,并计算对应每台发电机组出力分配的初始适应值。 (3)利用快速非支配排序和拥挤距离计算策略求取全局非劣最优解。 (4)通过计算方法函数更新粒子,计算更新后的适应值,求取更新后粒子目标函数值,并与上代对应值进行对比,得出此时最优目标函数值。 (5)获得子代种群后,将上代最优种群与其进行合并,并利用快速非支配排序和拥挤距离计算策略求取此时全局最优解,并产生下一代种群。 (6)如果粒子个数i (7)确认是否达到最大迭代次数λ,如果满足终止条件,则算法停止,输出各发电机组最优出力方案、总出力和目标函数值。本文算法计算经济节能调度框图如图3所示。 图3 计算方法经济节能调度框图Fig.3 Economic energy saving scheduling 为了验证本文提出的MFO算法用于求解电力系统环境经济调度的有效性和经济性,本节采用传统含有40台发电机组系统对MFO算法作进一步验证和分析。 同时考虑总煤耗成本和污染气体排放量,系统总负荷设为10500MW,40机组系统参数详见文献[15]。针对该测试系统,在MATLAB2014b平台上编制程序执行本文算法,设置MFO算法粒子数为100个,最大迭代次数为500次;文献[15]中非支配排序遗传算法(Nondominated Sorting Genetic Algorithm-Ⅱ,NSGA-Ⅱ)、帕累托进化算法(Strength Pareto Evolutionary Algorithm,SPEA2)、多目标差分进化算法(Multi-Objective Differential Evolution,MODE)、万有引力算法(Gravitational Search Algorithm,GSA)和帕累托差分进化算法(Pareto Differential Evolution,PDE)迭代次数设置为500次,单独运行200次,取最优调度方案。 多目标优化过程中,成本目标函数和排放量目标函数在进行500次迭代过程中的收敛曲线如图4所示。迭代次数150次时经济目标与环境目标均趋于稳定,可见,本文算法收敛性较好,可以较快实现调度方案的获取。 图4 MFO求解总燃料成本和污染排放目标收敛曲线Fig.4 Convergence curve of total fuel cost and pollutant emission target by MFO algorithm 为了权衡煤耗因素和污染排放因素对调度方案选取的影响,本文选用帕累托最优策略解决多目标优化过程中互相排斥目标间的合理配置,帕累托最优前沿的逼近问题可以将多目标分解为若干个单目标优化子问题,使成本($)与排放量(t)通过策略互相制约和约束。 图5为运用MFO算法在同时考虑煤耗费用和污染排放处理费用时,运用帕累托最优前沿对该仿真系统的最后一次迭代过程中20个非支配解的分布规律,并与文献[15]中PDE算法、MODE算法、SPEA2算法和NSGA-Ⅱ算法中非支配解进行对比。由图5可以看出,本文算法的最优解集在目标空间内分布更广,最优前沿面更优。图5中所标注区域为上述算法在最优前沿面上的最优点集合,比较非支配解可获得全局最优调度方案,即本文所提算法最优出力方案中多目标均分别优于文献[15]中所列算法的调度方案。 图5 帕累托最优前沿比较Fig.5 Pareto optimal frontier comparison 将所得调度方案同文献[15]中5种优化算法进行比较,结果如表1所示。本文算法所得最优总煤耗费用为125669.39$,低于NSGA-Ⅱ、SPEA2等优化算法调度结果;在总污染排放量的比较中,MFO算法所得调度方案将排放含硫、氮化合物为主的污染气体210300.66t,同样低于文献[15]中其他算法所得结果。通过对本文算法与文献[15]中算法求取该多目标优化问题的对比,可见本文算法在求解EED问题的经济性和有效性。 电力系统有功调度过程中,系统负荷的大小随时间、用户需求等因素改变。针对该测试系统,常规火电机组参数保持不变,通过对系统总负荷的改变对本文算法做进一步模拟。表2为系统总负荷达到6000MW、8000MW和10500MW时应用本文优化算法求解EED问题时各发电机组最优出力情况,该结果进一步验证了本文环境经济调度算法的有效性和适应性。 表1 不同算法的经济调度求解Tab.1 Solving of economic dispatch by different algorithms 表2 不同系统负荷的经济调度求解Tab.2 Solving of economic dispatch by different system loads 本文提出了求解多目标环境经济调度的帕累托最优MFO算法。采用罚函数法保证平衡约束条件,通过运用帕累托最优前沿求取多目标最优分配方案。计算和分析结果表明: (1)对于煤耗成本因素和污染排放因素,本文算法可以更好地适应两者的关系,并且收敛速度较快,收敛性强。 (2)在满足平衡约束和容量约束的前提下,与现有求解EED问题算法相比,本文算法具有更好的可行性。 (3)本文算法对于大规模规划问题的适用性较强,可以为节能减排的环境经济调度提供参考,具有非常广阔的工程应用前景。 [1] 刘静,罗先觉(Liu Jing,Luo Xianjue).采用多目标随机黑洞粒子群优化算法的环境经济发电调度(Environ-mental economic dispatching adopting multi-objective random black-hole particle swarm optimization algorithm)[J].中国电机工程学报(Proceedings of the CSEE),2010,30(34):105-111. [2] 江岳文, 陈冲, 温步瀛(Jiang Yuewen, Chen Chong, Wen Buying). 基于随机模拟粒子群算法的含风电场电力系统经济调度(Economic dispatch based on particle swarm optimization of stochastic simulation in wind power integrated system)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2007, 26(3):37-41. [3] 伍大清, 刘立, 郑建国,等(Wu Daqing, Liu Li, Zheng Jianguo, et al.). 基于环境经济调度问题的空间自适应划分多目标优化(Environmental economic power dispatch based on multi-objective evolution algorithm with adaptive space partition)[J]. 控制与决策(Control and Decision), 2015, 30(11):1974-1980. [4] Kuntal Bhattacharjee, Aniruddha Bhattacharya, Sunita Halder nee Dey. Backtracking search optimization based economic environmental power dispatch problems[J]. International Journal of Electrical Power & Energy Systems, 2015, 73: 830-842. [5] Hota P K, Barisal A K, Chakrabarti R. Economic emission load dispatch through fuzzy based bacterial foraging algorithm[J]. International Journal of Electrical Power & Energy Systems, 2010, 32: 794-803. [6] Bhattacharya A, Chattopadhyay P K. Application of biogeography based optimization for solving multi-objective economic emission load dispatch problems[J]. Electric Power Components and Systems, 2010, 38(3): 340-365. [7] Abdelaziz A Y, Ali E S, Abd Elazim S M. Combined economic and emission dispatch solution using flower pollination algorithm[J]. International Journal of Electrical Power & Energy Systems, 2016, 80: 264-274. [8] 谭忠富,鞠立伟,陈致宏,等(Tan Zhongfu, Ju Liwei, Chen Zhihong,et al.).基于粗糙集理论与CLSDE算法的环境经济调度优化模型(An environmental economic dispatch optimization model based on rough set theory and chaotic local search strategy differential evolution algorithm)[J].电网技术(Power System Technology),2014,38(5):1339-1345. [9] 陈功贵, 陈金富(Chen Gonggui, Chen Jinfu).含风电场电力系统环境经济动态调度建模与算法(Environmental/economic dynamic dispatch modeling and method for power systems integrating wind farms)[J].中国电机工程学报(Proceedings of the CSEE), 2013, 33(10): 27-35. [10] Mirjalili S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm[J]. Knowledge Based Systems, 2015, 89: 228-249. [11] Chen Po Hung, Chang Hong Chan. Large-scale economic dispatch by genetic algorithm[J]. IEEE Transactions on Power Systems, 1995,10(4):1919-1926. [12] 刘磊, 杨仕友(Liu Lei, Yang Shiyou). 高维多目标优化设计的改进多重单目标Pareto采样算法研究(An improved multiple single objective Pareto sampling algorithm for many-objective optimizations)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2013, 32(1): 89-93. [13] 崔逊学(Cui Xunxue).多目标进化算法及其应用(Applications adopting multi-objective evolutionary algorithm)[M].北京:国防工业出版社(Beijing: National Defence Industry Press),2006. [14] 冯士刚,艾芊(Feng Shigang,Ai Qian).带精英策略的快速非支配排序遗传算法在多目标无功优化中的应用(Application of fast and elitist non-dominated sorting generic algorithm in multi objective reactive power optimization)[J].电工技术学报(Transactions of China Electrotechnical Society),2007,22(12):146-152. [15] Güvenç U, Sönmez Y, Duman S, et al. Combined economic and emission dispatch solution using gravitational search algorithm[J]. Scientia Iranica, 2012, 19 (6): 1754-1762.3 用于多目标优化的MFO算法
3.1 MFO算法
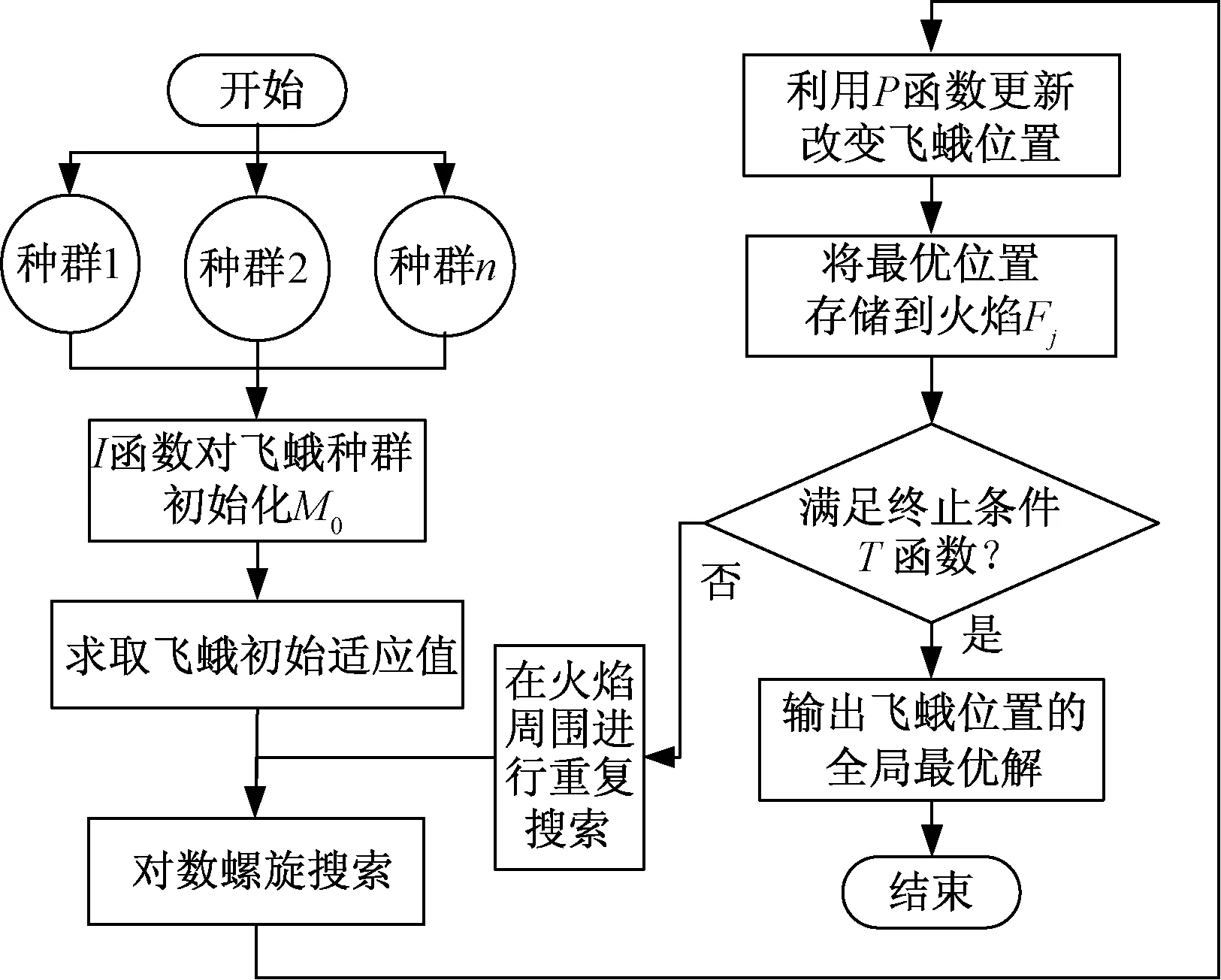
3.2 基于帕累托最优的MFO多目标优化
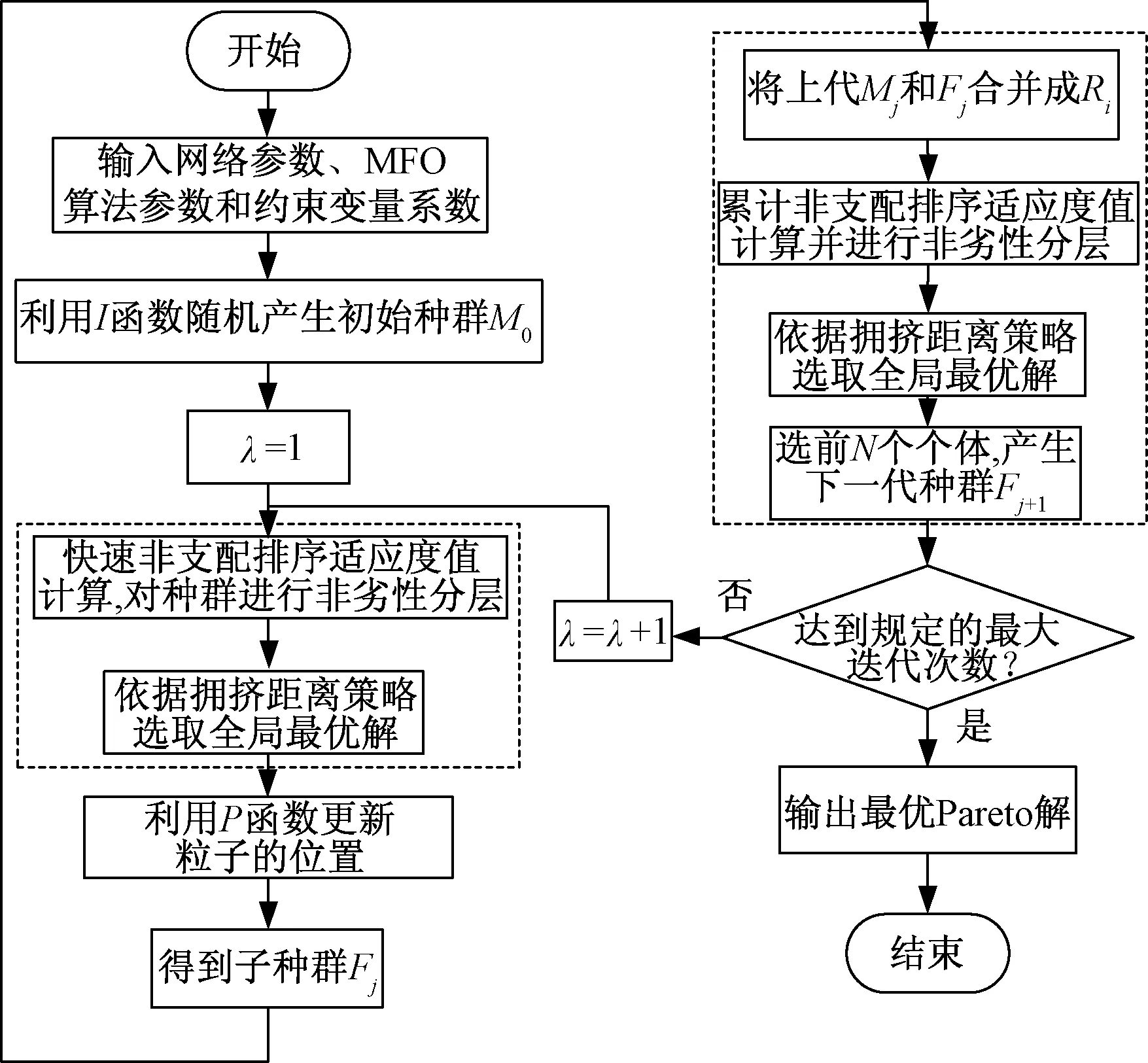
4 仿真分析
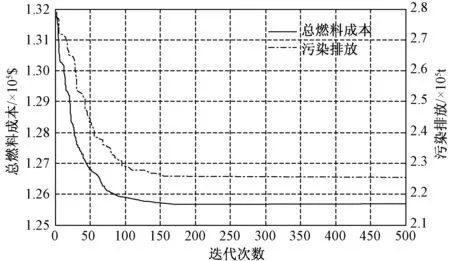
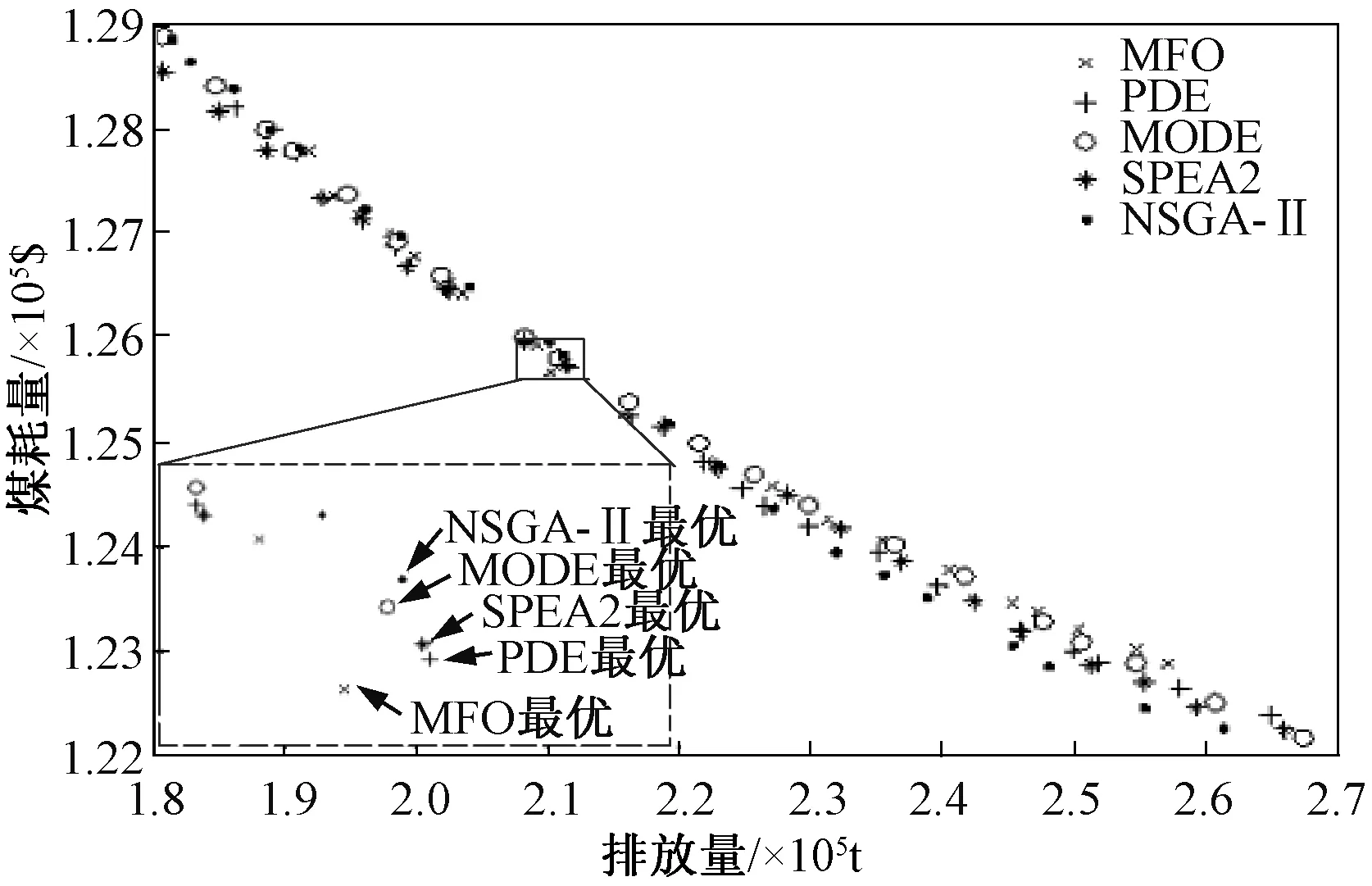
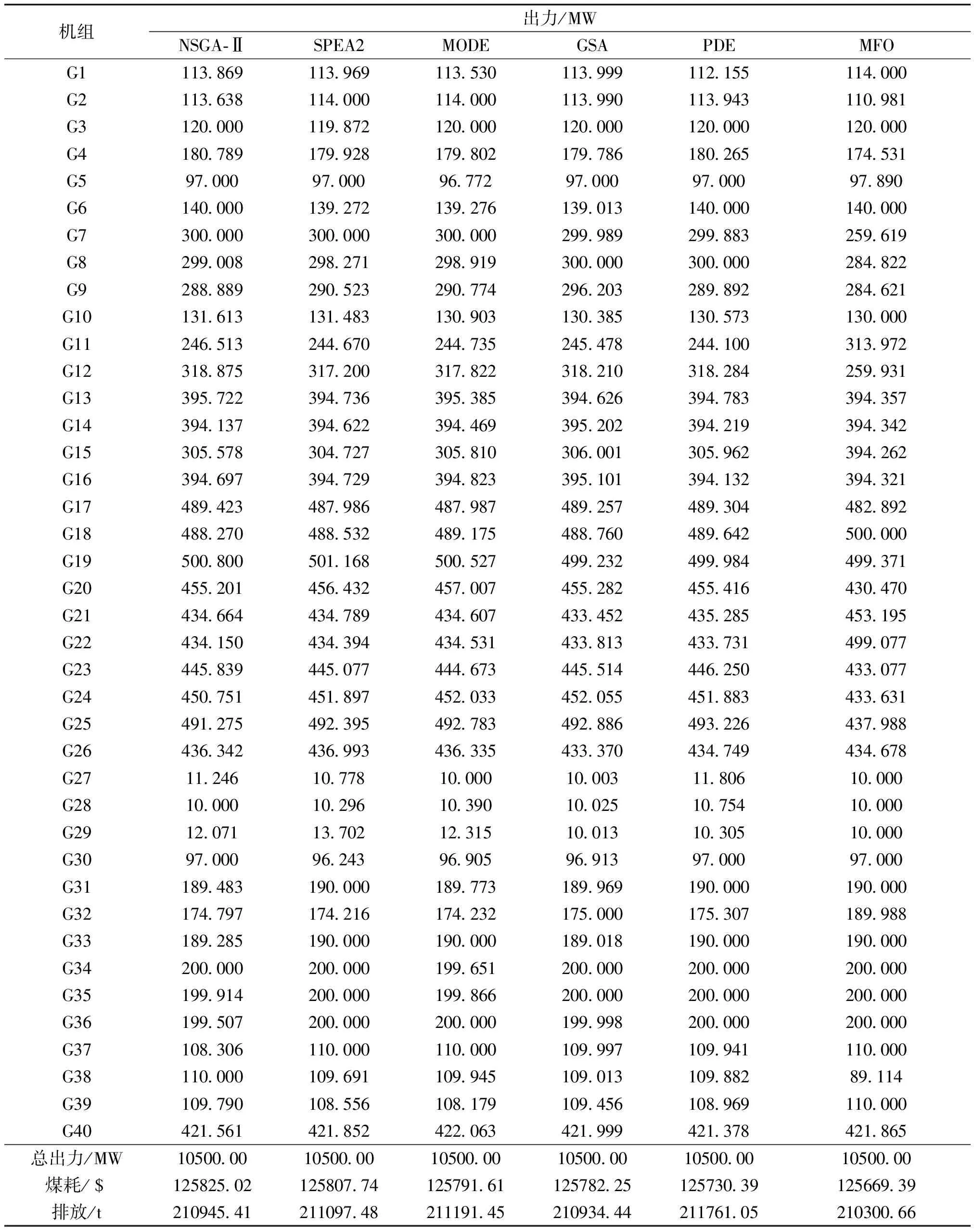
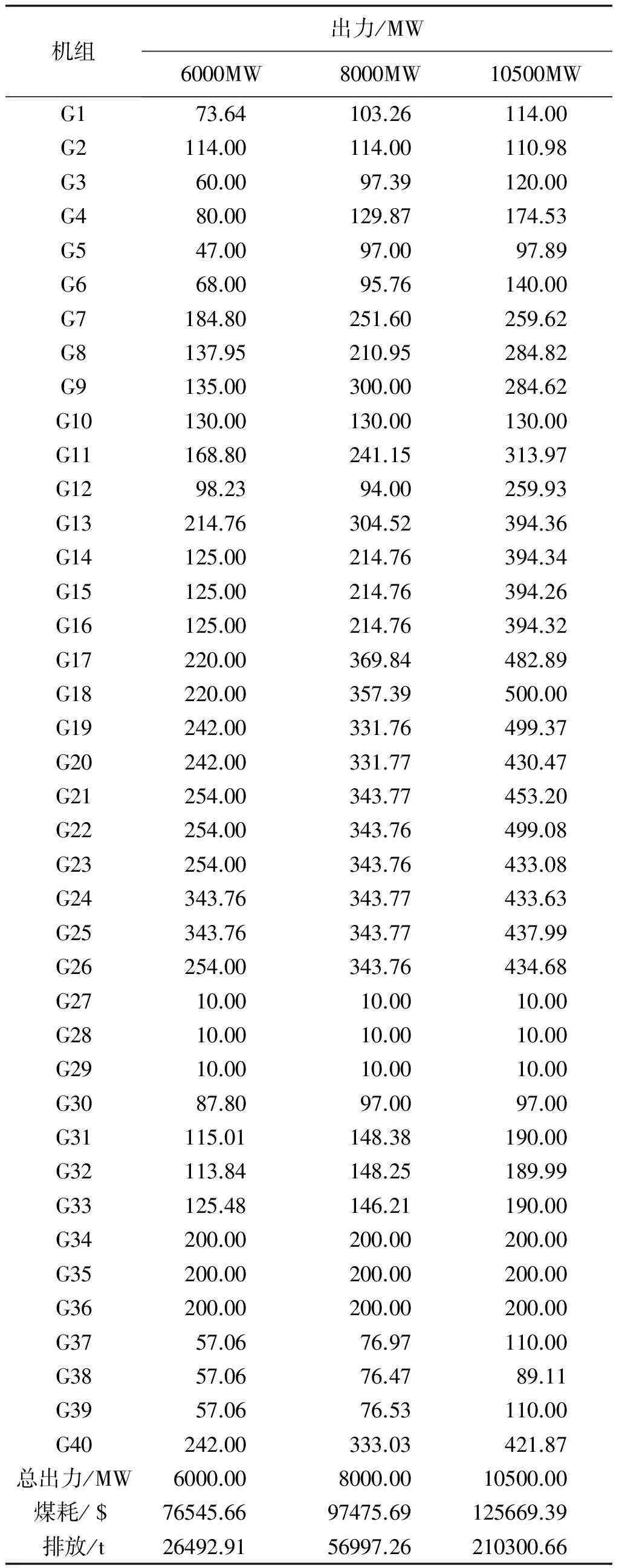
5 结论
