岩溶隧道在SH波激励下动力响应位移解析解

臧 万 军， 孙 文 涛

( 1.福建工程学院 土木工程学院， 福建 福州 350118； 2.地下工程福建省高校重点实验室, 福建 福州 350118 )

0 引 言

在地下结构地震动响应方面，研究方法主要有地震观测、模型试验和理论分析3种[1-2]，其各有优缺点，本文仅就理论分析研究予以阐述．理论分析研究分为数值模拟和理论解析两种方法．数值模拟比理论解析方法更接近于实际工况，但有时局限于本构模型的适用条件，与真实情况有所偏差；理论解析法对实际工况进行简化，在揭示物理力学本质方面具有优势，但在计算复杂边值问题上存在困难，如复变函数与其积分变换的计算等，简单模型尚且如此，复杂模型更是困难，为得到解析解需要做更多简化而与实际情况相去甚远，甚至无法得出结果．

国内外一些学者基于波函数展开法对地下结构动力响应问题进行了研究．梁建文等[3-4]研究了在P波和SV波激励下地下洞室群的动应力集中问题；孙红阳[5]、梁建文等[6]运用Fourier-Bessel级数展开法和镜像法，推导出半空间中地下洞室群在SH波入射下隧道位移解析解；杜金金[7]、付佳等[8]采用波函数展开法求解了单隧道在SH波入射下位移解析解．

以上学者仅就单洞隧道或隧道群作了研究，但在岩溶隧道[9]动力响应解析解方面研究较少．本文主要运用波函数展开法和Fourier-Bessel级数变换，推导岩溶隧道在平面SH波激励下动力响应位移解析解的计算公式，并研究溶洞半径、溶洞与隧道的中心距和平面SH波入射角度等因素对岩溶隧道动力响应位移幅值的影响，为岩溶隧道抗减震设计提供理论依据．

1 理论解析解推导

1.1 分析模型建立

岩溶形态及性质各异，在隧道施工和运营过程中对隧道影响较大的是具有一定规模和尺度的岩溶空洞．为简化分析、突出重点，本文不考虑溶洞充填物质．因此，本文中岩溶特指具有一定规模的岩溶空洞，将此类地质条件下的隧道称之为岩溶隧道．现建立如图1所示的简化模型，在一个均匀的半空间中，存在一溶洞和一隧道，溶洞半径为a1，圆心到地表距离为D，隧道半径为a2．溶洞与隧道的中心距为s．

图1 岩溶隧道模型及其镜像Fig.1 The model of karst tunnel and its mirror image

作如下假定：

(1)隧道衬砌为刚性；

(2)无限半空间为弹性、均质、各向同性．

假设一单位幅值为1的平面SH波入射，入射角度为γ，如图1所示．

1.2 波场分析

岩溶隧道模型为平面二维模型，z轴垂直于纸面，假定入射波为垂直于纸面沿着z轴作简谐振动．入射波满足波动方程[5]：

(1)

在极坐标系下圆心O1处SH波表达式如下：

(2)

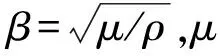
入射波波长λ的比值表达式如下：

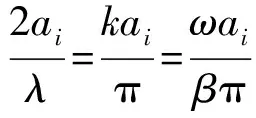
(3)

运用镜像法模拟边界条件为零应力的地表模型．

一波源处入射波的表达式见式(2)．通过镜像法，在地表边界另一波源，该入射波可表示为

(4)

入射波在传播过程中遇到溶洞和隧道异常区域后，发生散射效应，产生4组散射波，其表达式为

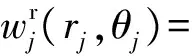
Bj，msinmθj)；j=1，2，3，4

(5)

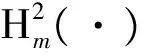
全空间的总位移场可表示为

(6)

利用内域型Graf加法公式，把外域型的模型转换到内域型Graf加法公式中进行计算，具体步骤详见文献[5]．

1.3 边界条件引入

溶洞表面边界处无荷载，引入模型应力和位移边界条件可得[5-6]

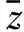
τr1z1=0 τr2z2+gw(z2，

2)=0

(7)

-ω2M′0Δ1=0 -ω2M0Δ2=-f

(8)

式中：M′0为溶洞单位长度质量，M0为隧道单位长度质量，Δ1、Δ2分别为溶洞和隧道位移幅值，f为隧道边界上单位长度上的力，g为隧道边界约束刚度系数．

1.4 位移解析解求解

解得溶洞和隧道的位移分别为

Δ1=J0(ka1)+exp(-2ikDcosγ)J0(ka1)×

(9)

Δ2=exp(-ikssinγ)J0(ka2)+exp(-2ikD×

cosγ-ikssinγ)J0(ka2)cosγ+

(10)

1.5 实用公式简化

为便于技术人员计算，根据Bessel函数的级数解和Bessel函数以及Hankel函数的性质，进一步作简化处理．

溶洞的位移公式整理为

Δ1=G+Gcosγ[cos(2kDcosγ)-

(11)

隧道的位移公式整理为

Δ2=G[cos(kssinγ)-isin(kssinγ)]+

G[cos(2kDcosγ+kssinγ)-

isin(2kDcosγ+kssinγ)]cosγ-

(12)

其中

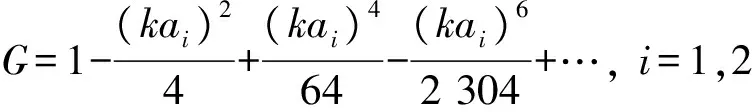
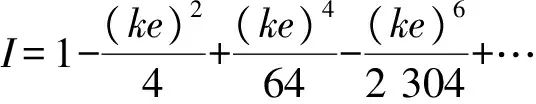
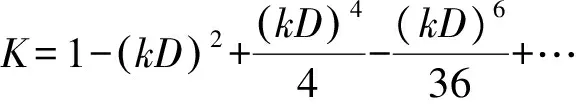
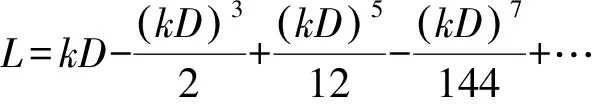
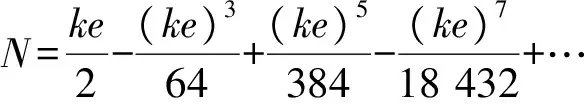
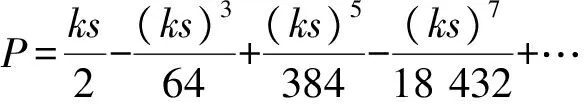
为求出实际地震动的位移时程曲线，基于Matlab软件通过快速傅里叶变换将地震波时程记录分解为若干间隔相等的覆盖0～21 Hz的不同频率分量，乘以对应的频域放大谱值，再把放大后的频域结果通过傅里叶变换得到相应的时域结果[7]．

2 理论解析解验证

岩溶隧道动力响应位移解析解的推导基于复变函数方法和工程波动理论，适用于均质、各向同性的岩溶隧道动力响应分析．为验证解析解的正确性，现与数值模拟解进行比较分析．

2.1 数值模拟模型

某岩溶隧道开挖半径为5 m，截面采用马蹄形，隧道中心到地表的距离为105 m．根据工程地质报告，计算物理参数见表1．

计算模型如图2所示．

表1 材料的物理力学参数Tab.1 Physico-mechanical parameters of materials

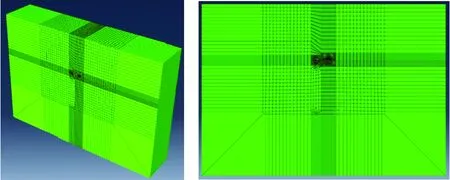
图2 岩溶隧道数值模拟三维模型Fig.2 The three-dimensional model of karst tunnel numerical simulation

马蹄形隧道轮廓和6个检测点如图3所示．

图3 隧道形状和6个检测点Fig.3 Tunnel shape and six monitoring points

2.2 马蹄形换算为圆形的可行性研究

为将马蹄形换算成圆形，先讨论该数值计算与解析解有无可比性．为不失一般性，现提取数值模拟解中隧道任意截面中仰拱、右拱脚、右拱肩、拱顶、左拱肩和左拱脚6个检测点的位移时程曲线进行比较．

地震波选用汶川地震波，经滤波基线校准的位移时程曲线如图4所示．

图4 汶川地震波经滤波基线校准的位移时程曲线Fig.4 The time-displacement curve of Wenchuan earthquake wave calibrated by filter baseline

在入射角度γ=0°和γ=90°时，隧道位移时程曲线如图5所示．

现给出2、4、6和8 s时的位移幅值(表2、3)．

(b)γ=90°

图5 隧道在入射角度γ=0°和γ=90°时的位移时程曲线

Fig.5 The time-displacement curve of tunnel atγ=0° andγ=90°

数值模拟解中隧道任意截面中拱顶、左拱肩、右拱肩、左拱脚、右拱脚和仰拱6个关键部位的位移时程曲线基本重合，波形一致，但6个关键部位的位移幅值的数据存在允许范围内的差异，如表2、3所示，说明隧道形状对位移影响较小，因此，在入射角度γ=0°、γ=90°时，推导位移解析解时把隧道简化为圆形是可行的．拱脚等断面突变位置在数值模拟中存在应力集中现象，6个关键部位应力曲线与上述位移曲线不同，故若推导应力解析解，不能直接把隧道简化为圆形．

表2 2、4、6和8 s的测点位移幅值(γ=0°)Tab.2 Displacement amplitude of monitoring points at 2, 4, 6 and 8 s (γ=0°)

表3 2、4、6和8 s的测点位移幅值(γ=90°)Tab.3 Displacement amplitude of monitoring points at 2, 4, 6 and 8 s (γ=90°)

2.3 数值模拟解与理论解析解的比较

取数值模拟解中溶洞和隧道拱顶的位移时程曲线与解析解进行比较，结果如图6所示．

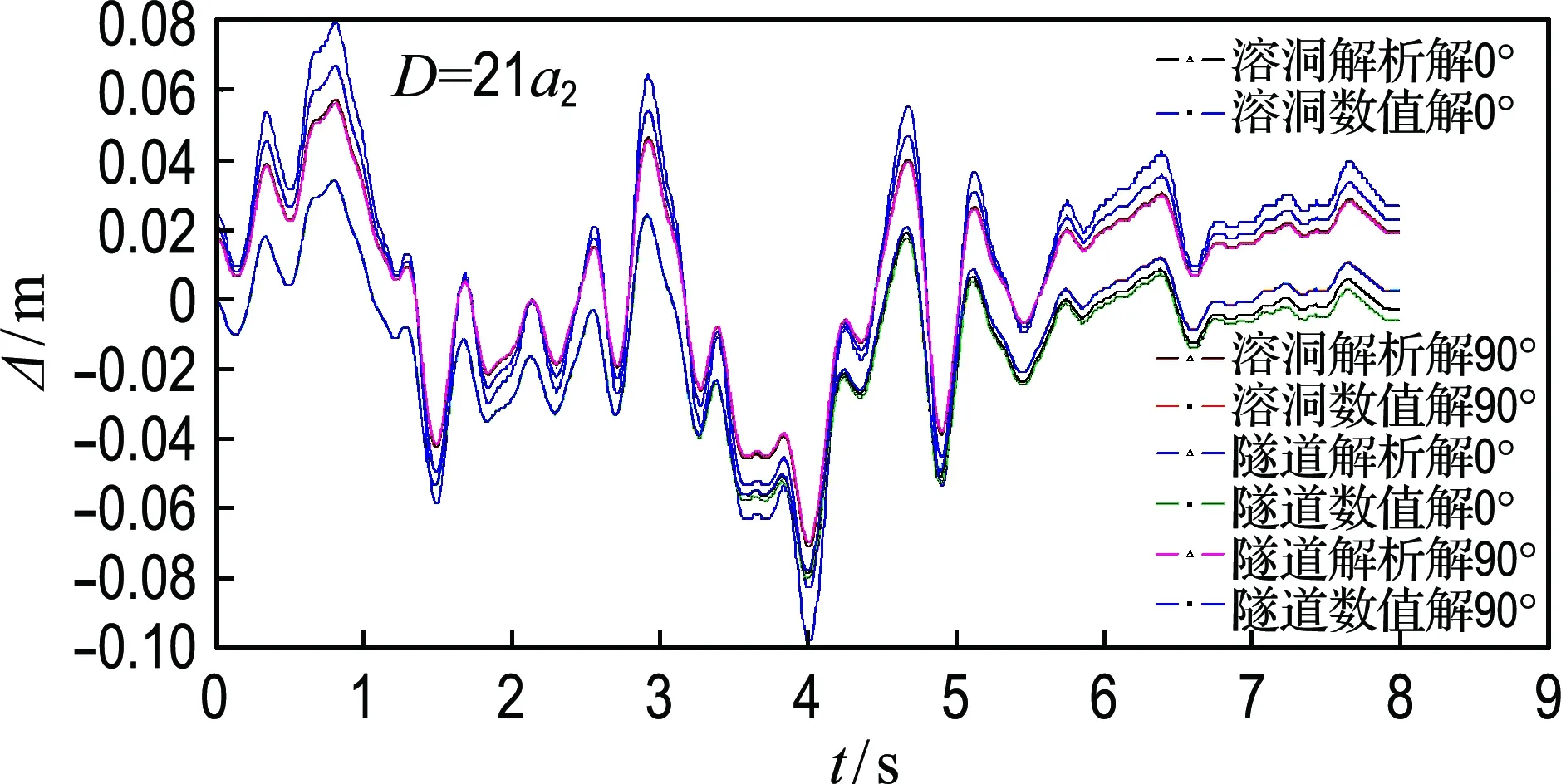
图6 溶洞和隧道的位移时程曲线Fig.6 The time-displacement curve of karst cave and the tunnel

由图6可以看出，数值解和解析解位移时程曲线中第1～5 s吻合较好，而前1 s和后3 s相差较大．比较溶洞和隧道在入射角度γ=0°和γ=90°时解析解和数值解的位移幅值峰值可知，溶洞的位移幅值峰值在入射角度γ=0°和γ=90°时分别相差11%和9%，隧道的位移幅值峰值在入射角度γ=0°和γ=90°时分别相差9%和10%，可见理论解析解具有较好的精度．

3 算 例

3.1 地震动输入

理论解析所用地震波采用2008年汶川地震中的卧龙波，持时8 s．其中地震峰值位移为-0.062 m．地震波波形如图4所示．

3.2 解析解影响因素分析

根据解析解，考虑溶洞半径、溶洞与隧道中心距以及平面SH波入射角度等因素[10]，探讨岩溶隧道在SH波激励作用下的地震动力响应规律．计算工况如表4所示．

表4 工况说明表Tab.4 The table of working condition

各工况溶洞和隧道位移时程曲线如图7所示．

从图7(a)可以看出，工况1溶洞位移峰值略微比工况3的大0.14%，工况1隧道位移峰值比工况3的大28%；从图7(b)可知，工况2溶洞位移峰值比工况4的大0.57%，工况2的隧道位移峰值比工况4的大7%．说明当平面SH波入射角度相等，溶洞与隧道间的中心距相等时，溶洞半径越大，溶洞与隧道的位移幅值越大．

从图7(a)可知，工况3溶洞位移峰值比工况5对应值小4%，工况3隧道位移峰值比工况5的小4%；从图7(b)可知，工况4溶洞位移峰值比工况6的对应值小1.5%，工况4隧道位移峰值比工况6的小9%．说明当平面SH波入射角度固定，溶洞半径相等时，溶洞与隧道间的中心距越小，溶洞与隧道的位移幅值越大．

从图7(c)、(d)可以看出，平面SH波入射角度为90°时的位移峰值大于入射角度为0°时的对应值，增幅从1.80%、2.57%、5.79%、6.00%、21.00%到24.00%不等，在总体上说明当溶洞半径相等，溶洞与隧道间的中心距相等时，平面SH波入射角度越大，溶洞与隧道的位移幅值越大．

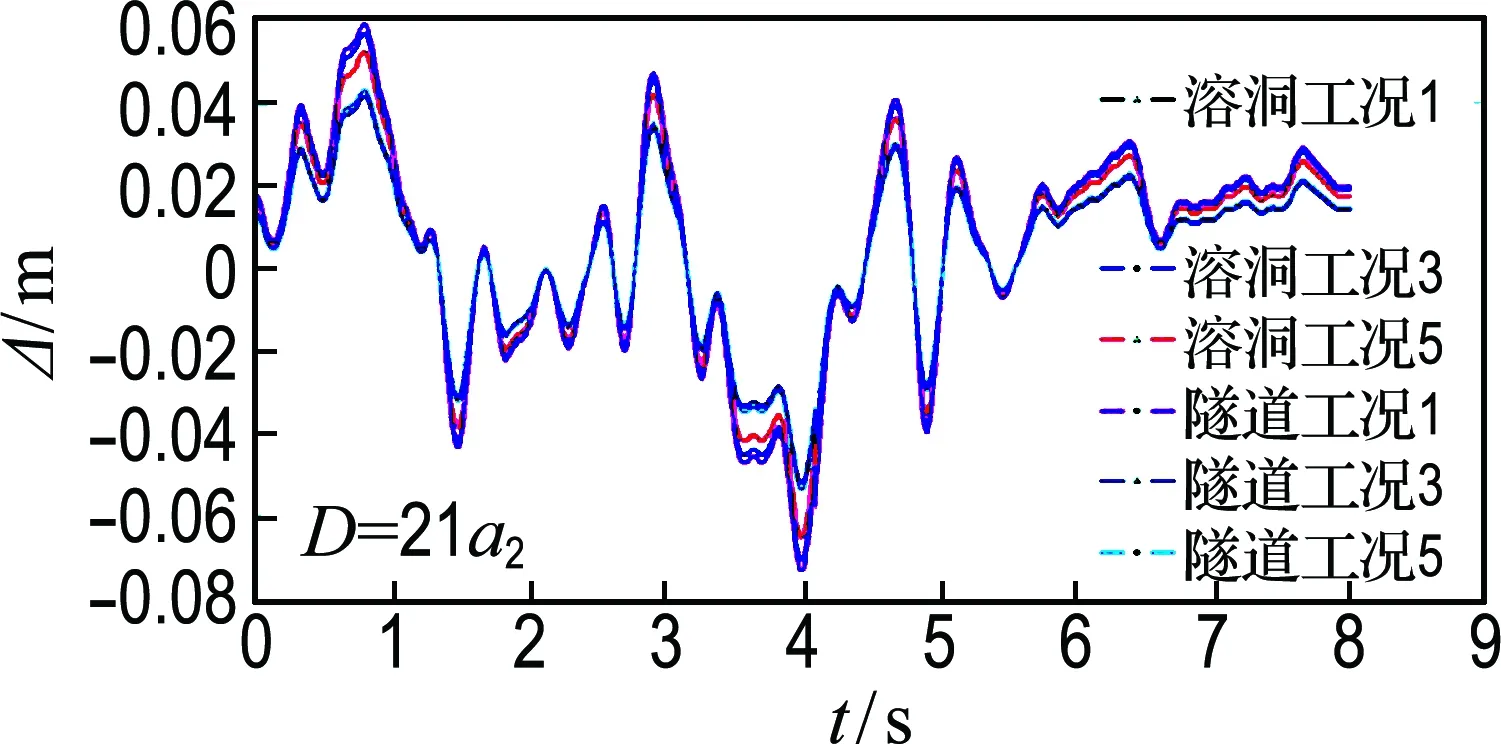
(a) 工况1、3、5的比较

(b) 工况2、4、6的比较

(c) 溶洞

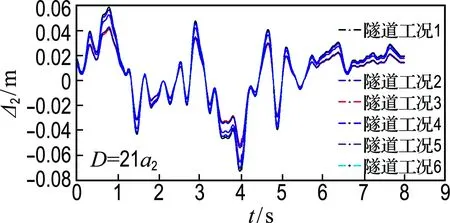
(d) 隧道

图7 不同工况溶洞和隧道位移时程曲线

Fig.7 The time-displacement curve of karst cave and tunnel at different cases

4 结 论

(1)基于工程波动理论，利用波函数展开法和Fourier-Bessel级数变换，推导了岩溶隧道在平面SH波激励下动力响应位移解析解的计算公式，并提出了实用的简化解．

(2)通过数值模拟解验证了动力响应位移解析解的合理性．数值模拟解和解析解位移时程曲线基本吻合，在波形上保持一致．溶洞和隧道在平面SH波激励作用下的位移幅值峰值相差10%左右，表明解析解具有较好的精度．

(3)研究了溶洞半径、溶洞与隧道间的中心距以及平面SH波入射角度等3个影响因素对溶洞和隧道的动力响应作用，发现溶洞和隧道位移幅值与溶洞半径成正比，当溶洞半径由0.5a2增大到a2时，隧道的位移幅值会增大7%～28%；溶洞和隧道位移幅值与两者中心距呈反比，当溶洞与隧道中心距从2.5a2增加到4.0a2时，溶洞和隧道的位移幅值会减小1.5%～9%；溶洞和隧道的位移幅值与平面SH波入射角度成正比，当入射角度γ从0°增大到90°时，溶洞与隧道的位移幅值增幅从1.80%、2.57%、5.79%、6.00%、21.00% 到24.00%不等．

[1] 王国波,袁明智,苗 雨. 结构-土-结构相互作用体系地震响应研究综述[J/OL]. 岩土工程学报, 2017:1-10. [2017-08-14]. http://kns.cnki.net/kcms/detail/32.1124.TU.20170814.1622.030.html.

WANG Guobo, YUAN Mingzhi, MIAO Yu. A review of seismic response of structure-soil-structure interaction system [J/OL].ChineseJournalofGeotechnicalEngineering, 2017:1-10. [2017-08-14]. http://kns.cnki.net/kcms/detail/32.1124.TU.20170814.1622.030.html. (in Chinese)

[2]张玉敏. 大型地下洞室群地震响应特征研究[D]. 武汉:中国科学院武汉岩土力学研究所, 2010.

ZHANG Yumin. Study on response characteristics of large underground cavern group under earthquake [D]. Wuhan: Institute of Rock and Soil Mechanics Chinese Academy of Sciences, 2010. (in Chinese)

[3]梁建文,张 浩,VINCENT W L. 平面P波入射下地下洞室群动应力集中问题解析解[J]. 岩土工程学报, 2004,26(6):815-819.

LIANG Jianwen, ZHANG Hao, VINCENT W L. An analytical solution for dynamic stress concentration of underground cavities under incident plane P waves [J].ChineseJournalofGeotechnicalEngineering, 2004,26(6):815-819. (in Chinese)

[4]梁建文,张 浩,VINCENT W L. 地下双洞室在SV波入射下动力响应问题解析解[J]. 振动工程学报, 2004,17(2):132-140.

LIANG Jianwen, ZHANG Hao, VINCENT W L. An analytical solution for dynamic stress concentration of underground twin cavities due to incident SV waves [J].JournalofVibrationEngineering, 2004,17(2):132-140. (in Chinese)

[5]孙红阳. 地下隧道群在SH波作用下动力响应解析解[D]. 天津:天津大学, 2014.

SUN Hongyang. Analytical solutions for dynamic response of underground tunnels under SH waves [D]. Tianjin: Tianjin University, 2014. (in Chinese)

[6]梁建文,孙红阳. 隧道-土-隧道轴向动力相互作用的一个解析解[J]. 地震工程与工程振动, 2015,35(2):48-62.

LIANG Jianwen, SUN Hongyang. Dynamic tunnel-soil-tunnel interaction in longitudinal direction: an analytical solution [J].EarthquakeEngineeringandEngineeringDynamics, 2015,35(2):48-62. (in Chinese)

[7]杜金金. 地下隧道在SH波作用下动力响应解析解[D]. 天津:天津大学, 2012.

DU Jinjin. Analytical solutions for dynamic response of underground tunnels under SH waves [D]. Tianjin: Tianjin University, 2012. (in Chinese)

[8]付 佳,梁建文,杜金金. 平面SH波激励下的土-隧道动力相互作用的解析解[J]. 岩土工程学报, 2016,38(4):588-598.

FU Jia, LIANG Jianwen, DU Jinjin. Analytical solution of dynamic soil-tunnel interaction for incident plane SH wave [J].ChineseJournalofGeotechnicalEngineering, 2016,38(4):588-598. (in Chinese)

[9]马 群. 溶洞对隧道围岩稳定性影响分析及其探测方法研究[D]. 重庆:重庆大学, 2016.

MA Qun. Study on the influence of surrounding rock stability effected by karst cave and its detecting method [D]. Chongqing: Chongqing University, 2016. (in Chinese)

[10]梁 波,王志勇,刘德功. 溶洞存在对隧道的地震动力响应的影响分析[C] // 第三届全国水工岩石力学学术会议论文集. 上海:中国岩石力学与工程学会, 2010:217-221.

LIANG Bo, WANG Zhiyong, LIU Degong. Analysis about the tunnel dynamic response of earthquake on the influence of the existence of cave [C] //The3rdNationalConferenceonHydraulicRockMechanics. Shanghai: Chinese Society for Rock Mechanics and Engineering, 2010:217-221. (in Chinese)