洪水预报经验模型的混合蛙跳优化率定

司存友 ，卢婉莹 ，罗俐雅

（1. 江苏省水文水资源勘测局，江苏 南京 210029；2. 北京金水信息发展有限公司，北京 100000）

0 引言

洪水预报经验模型由于操作简便，能较好地阐述水文规律，目前在水文业务中应用十分广泛，为防汛及水资源调度利用等工作提供了至关重要的决策依据。但是洪水预报经验模型的参数在确定时具有较高的难度，需要通过多次循环往复的参数率定加以确定。江苏省采用的经验模型主要是 API 模型，场次洪水降水量P、前期影响雨量Pa、径流深R三要素及单位线的推求计算比较复杂。API 模型的参数优化率定更是一项繁琐、耗时、困难的工作，快速高效地寻求模型最优参数已成为水文模型应用研究的关键[1–2]。

江苏省洪水预警预报平台成功实现了高效率的人机交互，可以帮助业务人员完成 API 模型的场次洪水选择、次洪三要素（P，Pa，R）计算、相关图拟合、产流方案误差评定、单位线推求和综合、预报方案评定等过程的在线处理，并引入改进的遗传算法、人工蜂群、混合蛙跳等基于仿生学的人工智能优化算法实现经验模型的智能优化定线。其中混合蛙跳算法（SFLA）是一种模拟青蛙觅食行为的智能优化算法，具有参数少，鲁棒性强，简单易理解等特点，但目前还未引入到洪水经验模型参数优化方面，因此针对混合蛙跳定线进行研究。

1 API 模型结构和相关线型

1.1 模型结构

以前期影响雨量Pa表示土壤干湿程度的指标，以K代表土壤含水量的日消退系数，则

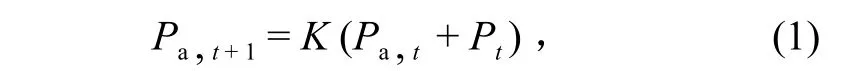
式中：Pa,t为t日上午 8 时的前期影响雨量；Pa值以土壤最大缺水量Imax作为上限控制，Imax按经验选择和对比计算确定；消退系数K一般为：

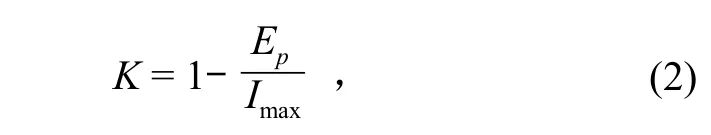
式中：Ep代表流域日蒸发能力。

前期影响雨量由经验计算公式确定：

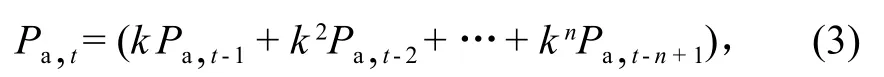
式中：n为影响本次径流的前期降雨天数，常取 15 d左右；k为常系数，一般可取 0.85 左右。

对无雨日，前期影响雨量Pa,t为：

通过式 (1)～(4)，计算降水量、前期影响雨量、径流量，点绘降雨径流相关图并定线，进行产流计算。但是人工拟合降雨径流相关图的精度不太理想，因此通过引入混合蛙跳算法对降雨径流相关图基本线型的参数进行率定，以得到拟合度较高的曲线。

1.2 相关线型

1）线簇线性相关线。这一类相关线是由一组线性相关线形成的簇，基本表达式为：

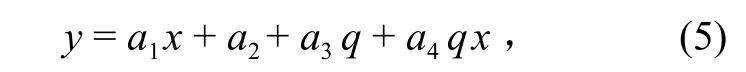
式中：y为预报对象；x为预报主因子；q为辅助因子；a1，a2，a3，a4为待定系数，受以下约束条件约束，a1＞ 0，0.02 ＞a3＞ 0，0.10 ＞a1＞ 0。

2）非线性相关线。非线性相关线是由 1 条或多条曲线组成的非线性相关线，本研究主要选用二次抛物线型为非线性相关线的基本线型，表达式为：

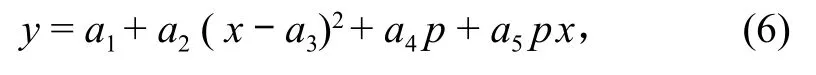
或

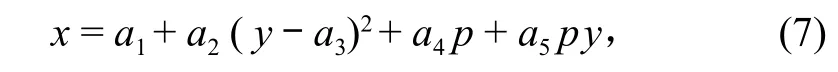
式中：x为横坐标变量，作为预报对象；y为纵轴变量，为主因子变量；p为第三变量；a5为待定系数。

式 (3) 为垂直型抛物线，式 (4) 为水平抛物线函数表达式。在计算中，需要计算垂直型抛物线反函数，表达式为：

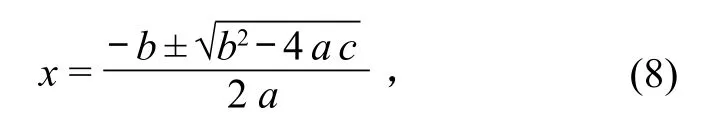
式中：a=a2，b=a5p a- 2a2a3，c=a1+a2+a4p a-y，a的正负号与a2的正负号一致。

2 混合蛙跳算法

2.1 定义及内涵

SFLA 是由 Eusuff 和 Laney 于 2003 年提出的一种全新群体智能进化算法，汲取了基于遗传因子的模拟演算法和基于群体觅食的粒子群算法的特点，模拟青蛙群觅食过程中的协同工作，进行全局和局部搜索，使算法不断向全局最优解逼近，具有较强的灵活性和通用性[3]。该算法适用于连续空间域的优化问题，主要应用在函数、组合、单目标、多目标等优化方面[4]。

2.2 计算方法

SFLA 是一种基于群体智能的后启发式新颖的进化算法[5]，具体过程如图 1 所示。

具体步骤如下：

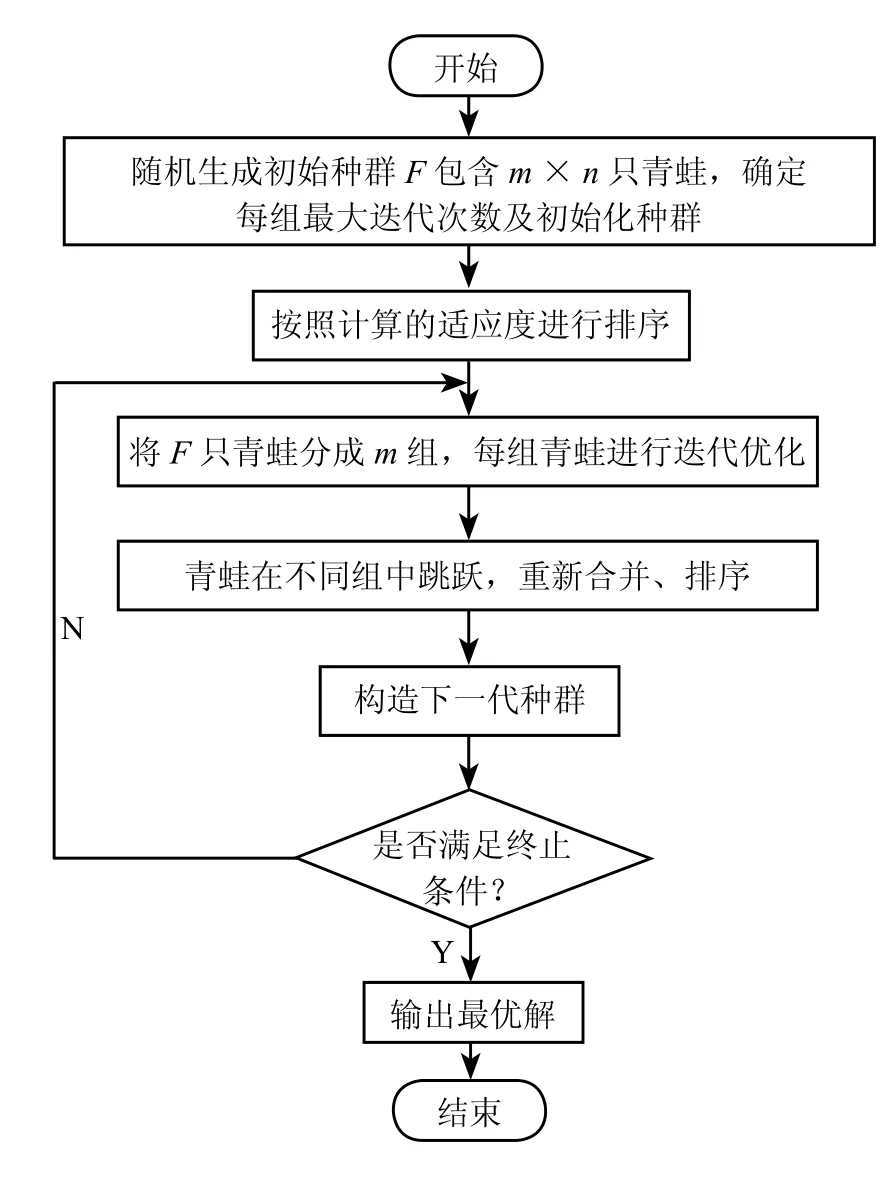
图 1 混合蛙跳算法流程图

1）对蛙群的各种参数进行初始化。每一只青蛙代表青蛙的当前位置，用这只青蛙的适应度表示。第i只青蛙表示为

2）按照适应度排序。将所有青蛙按照指定的适应度进行升序排列，组成数组适应度，并带有索引值，将每只青蛙按照适应度的排序进行排序。因此排在首位的青蛙是全局最优的青蛙，用Pg表示。

3）对青蛙划分模因组。将整个种群分成m组，每组包含n只青蛙。第 1 组内包含第 1 只青蛙，第（m+ 1）只青蛙，第（2m+ 1）只青蛙，以此类推。第 2 组包含第 2 只青蛙，第（m+ 2）只青蛙，第（2m+ 2）只青蛙，以此类推。第 3 组分配方式类似第 1 和 2 组，直至分配完毕。

4）在组内进化。n只青蛙在组内更新，在组内迭代Ne次，Ne为设定的最大迭代次数。组内位置最优青蛙为Pb，位置最差青蛙为Pw，利用步长Si更新公式：Si=rand( ) × (Pb-Pw)，Si∈[Smin，Smax]。

其中rand( ) 是随机取 0 到 1 之间的任意数，并确保Si在最小步长Smin与最大步长Smax的范围之内。更新位置最差青蛙Pw，当计算各点的适应度小于给定值ε，则停止迭代计算。混合蛙跳算法从组内最差青蛙出发，分别利用组内和全局最优与最差青蛙之间插值作为步长基数，获得更优的青蛙。在迭代过程中最差青蛙一直被更新，最终组内最优青蛙（最大值）、最差青蛙（最小值）趋近于一个值，即为求得的最优值。

2.3 目标函数

混合蛙跳算法的寻优策略确定各个参数的值，最优解即参数的值，从径流深实测数据出发，寻求一组参数，可采用方案的评定精度或与实际观测数据的方差作为目标函数，按给定的目标函数的度量方式达到最佳拟合[6]。

3 应用实例

本研究以小许庄站为例，分别采用混合蛙跳和传统定线 2 种方法进行降雨径流相关图的绘制，并对 2 组图线进行对比。

小许庄站位于黄泥河下游，1956 年 7 月设站，位于连云港市东海县安峰镇戴庄村，上游干流长度为 25 km，测站控制流域面积为 382.07 km²。

对小许庄站 1956—2013 年洪水选取单峰洪水，最终得到 71 场有效洪水。以径流深为预报对象，以（P+Pa）为主因子，采用二次抛物线型。

1）混合蛙跳应用。参考相关文献 [3] 和 [7]，并结合本次优化参数个数设置模因组数m= 5，初始化一组参数值即每组青蛙个数n= 20，局部迭代次数N=10，固定进化代数G= 100，函数变量维数S=30。根据模型算法程序循环计算的最优结果如表 1 所示。

表 1 混合蛙跳算法模型计算结果

根据非线性相关线公式，通过算法编程根据混合蛙跳得出系数，由此得到的拟合相关线函数关系表达式为：R= 0.000 9 (P+Pa)2+ 0.451 2 (P+Pa) -20.584。

生成的降雨径流相关图如图 2 所示，经过方案评定，合格率为 86.1%，精度评定为甲等方案。

2）传统定线方法。根据 71 场有效洪水，对Pa，P，R进行绘制，点绘R=f(P+Pa)，如图 3 所示。

经过评定，对 71 场洪水预报合格率为 73.9%，预报精度分别达到乙等和甲等。经过对比，混合蛙跳法在预报方案精度上高于传统定线方法，能够有效提高洪水预报精度。

4 结语

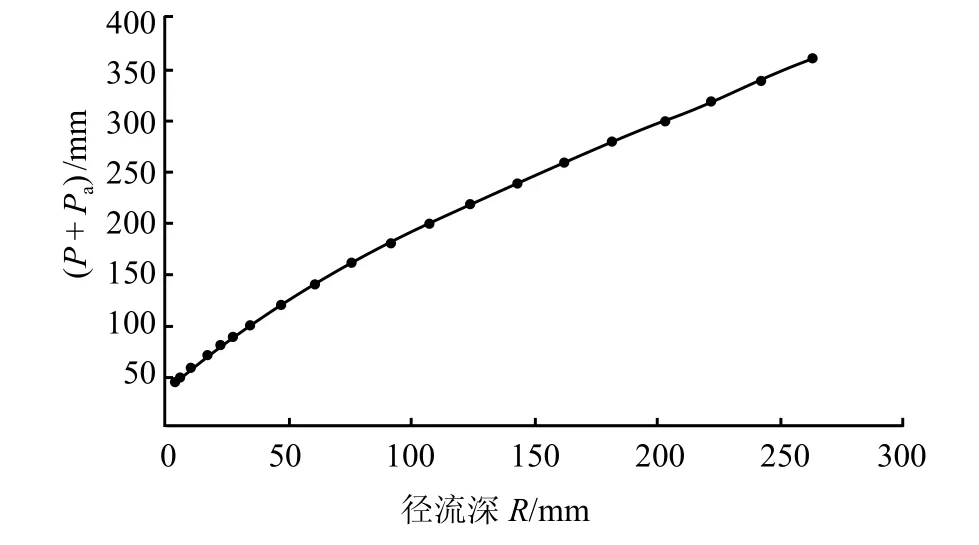
图 2 混合蛙跳法降雨径流相关图

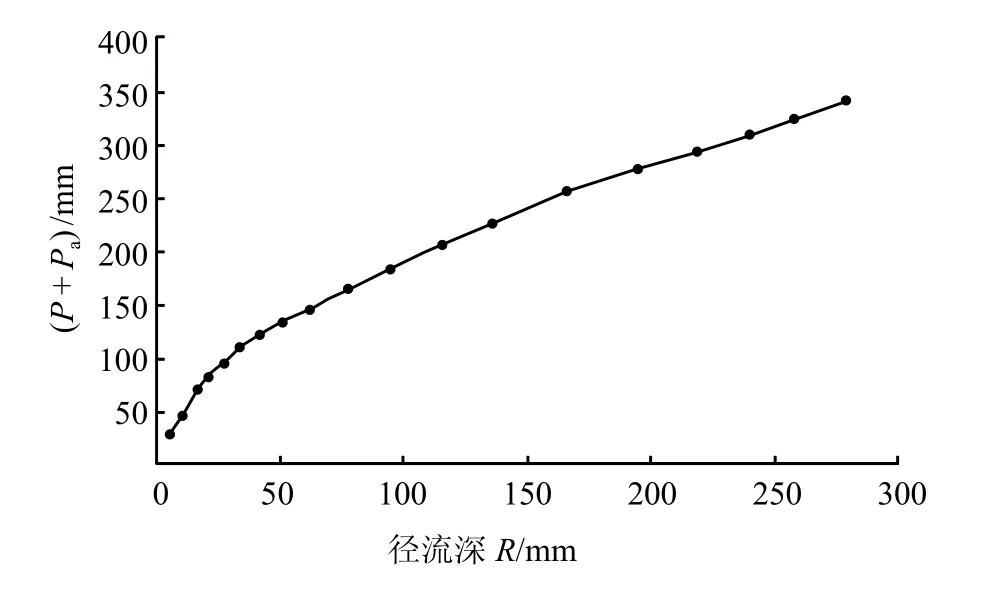
图 3 传统定线法降雨径流相关图

API 模型作为一种传统的经验方法，操作简便，同时涵盖了较多的水文特征信息，在实际洪水作业中仍然具备较高的应用与研究价值。以往混合蛙跳的研究主要在于对方法本身的改进和对新安江模型参数的优化，而 API 模型在现阶段洪水预报作业中应用比新安江模型更为广泛，因此探索混合蛙跳法在 API 模型中的应用具有一定实际意义。本研究通过混合蛙跳法，优化了 API 模型的参数率定，实现了计算机的智能自动定线，并通过应用实例证明本方法可以有效提高 API 模型预报精度。但是，混合蛙跳方法的参数设置对模型预报也有一定影响，今后可以进一步深入研究。

[1] 程海云，葛守西，邹冰玉. 相关图实时预报技术研究[J].水利水电快报，2008，29 (3): 16-18.

[2] 张端虎. 相关图洪水预报方案编制的自动化处理方法探讨[J]. 广东水利水电，2009 (1): 68-71.

[3] 李建军，郁滨，陈武平. 混合蛙跳算法的改进与仿真[J].系统仿真学报，2014，26 (4): 755-760.

[4] 高建兴. 混合蛙跳算法应用研究[J]. 网络安全技术与应用，2014 (7): 28-29.

[5] 王怡然. 改进的混合蛙跳算法及其多目标优化的应用研究[D]. 兰州：甘肃农业大学，2013.

[6] 张端虎. 改进复合形法在相关图水文预报方案建模中的

[7] 火久元，刘立群，赵红星，等. 基于混合蛙跳算法的水文模型参数估计方法[J]. 重庆理工大学学报，2016，30 (3):80-86.应用[J]. 广东水利水电，2012 (12): 34-36.