陕西省F2等级砝码计量比对不确定度评定实例

/ 西安计量技术研究院

0 引言

按照陕西省质量技术监督局的要求，西安计量技术研究院作为主导实验室组织陕西省的法定计量检定机构F2等级砝码计量砝码比对工作， 8个地级市计量所、1个县级市计量所以及3家省局授权计量检定机构参加此次比对。

1 测量过程

实验方法和过程依据JJG 99-2006《砝码》检定规程。砝码校准点、校准方法和校准次数参见表1。根据标准装置的实际情况，保留合适的有效位数。下面评定用E2等级标准砝码校准F2等级标准砝码得到折算质量修正值的不确定度。

表1 校准方法及校准次数

2 实验室环境控制

实验室应具有稳定的环境条件，按照JJG 99-2006的要求，实验室温度变化应满足每4 h最大变化3.5 ℃，空气相对湿度应在30%～70%范围之内，且每4 h最大变化不超过15%，实验室不允许有容易察觉的振动和气流，应尽量远离振源和磁源并避免阳光直接照射到仪器设备，以减小环境条件对校准的影响。本实验室在实际测量中环境温度为20.5 ℃，每4 h最大变化为0.4 ℃；相对湿度为68%，每4 h最大变化为2%；实验室大气压为953.9 hPa；根据空气密度的近似公式计算得出空气密度为1.124 6 kg/m3。

3 测量模型

由于砝码的折算质量修正值为直接测量法得到，其测量模型为

式中：mct—— 被检砝码的折算质量值；

mcr—— E2等级标准砝码的折算质量值；

C—— 空气浮力修正因子；

mcs—— 灵敏度砝码折算质量值；

mcw—— 配平砝码折算质量值

针对砝码的不同测量点的测量值，其测量不确定度均可按照以下方法进行评定，各测量点应引用各自的实际测量数据。

4 不确定度影响因素

影响砝码折算质量修正值的因素有：

1）砝码测量重复性引入的不确定度分量u1

2）E2等级标准砝码引入的不确定度分量u2

3）空气浮力引入的不确定度分量u3

4）质量比较器分辨力引入的不确定度分量u4

5）质量比较器偏载引入的不确定度分量u5

6）衡量仪器灵敏度引起的不确定度分量u6

7）砝码磁性引入的不确定度分量u7

8）其他影响因素

5 各分量的标准不确定度的评定

5.1 重复性分量引入的标准不确定度u1 (按A类方法进行评定)

对砝码的各个测量点，在相同条件下进行10次重复测量，按式（2）和式（3）计算各测量结果中此分量的标准不确定度。

单次实验标准偏差公式为

算术平均值的实验标准偏差公式为

本次校准用ABBA法测量，循环次数为10次，所以n= 10。本院测量数据见表2。

表2 折算质量修正值（单位：mg）

根据式（2）和式（3）计算各测量点的测量数据及重复性引入的标准不确定度，如表3所示。

表3 u1的评价

5.2 E2等级标准砝码引入的标准不确定度u2 (按B类方法进行评定)

针对不同测量点采用的标准砝码的不确定度，计算由此引入的标准不确定度分量u2，其结果按照式（4）进行计算。

砝码折算质量修正值的扩展不确定度U不大于相应准确度等级的最大允许误差绝对值的三分之一。

uinst(mcr)是标准砝码质量的不稳定性引起的不确定度，根据砝码7年的检定证书（见表4），利用贝塞尔公式既式（5）进行计算：

表4 E2等级标准砝码7年的折算质量修正值（单位：mg）

根据表4、式（4）和式（5）计算得出u2,见表5。

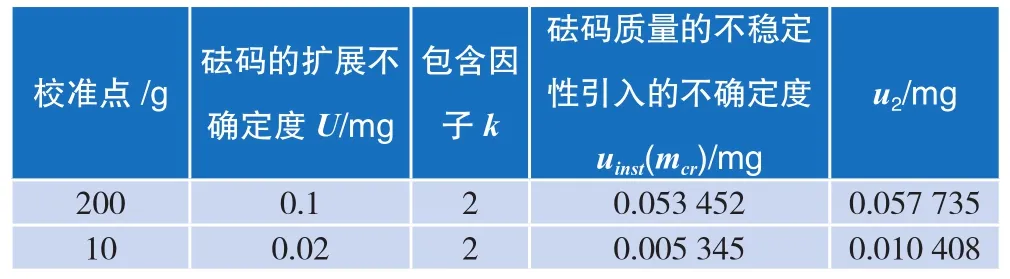
表5 u2的评价

5.3 空气浮力引入的不确定度u3

如果空气浮力修正值小于该砝码最大允许误差的九分之一，可不进行空气浮力修正，而将此部分误差放入空气浮力不确定度进行计算。

5.3.1 空气浮力修正值

空气浮力修正值按式（6）进行计算

式中：m0—— 砝码的标称值；

ρ0—— 空气密度参考值 1.2 kg/m3；

ρa—— 实验室的空气密度值1.124 6 kg/m3

因为本次比对没有测试砝码的体积，为保险起见，本次计算中采用极差法进行计算，取E2等级标准砝码密度最大值ρr= 8 030 kg/m3；取F2等级被检砝码密度最小值，ρt= 7 970 kg/m3来进行相关计算。

m0│C│远小于该砝码最大允许误差的九分之一，可不进行空气浮力修正，而将此部分放入空气浮力不确定度进行计算。

5.3.2 空气浮力修正的不确定度按照式（7）进行计算

式中：ρal—— 用更高等级的标准砝码检定标准砝码时的空气密度，省院查询得到ρal=1.13 kg/m3；

u(ρr) —— E2等级标准砝码密度的不确定度，可从其密度范围7 970～8 030 kg/m3计算得出，认为符合均匀分布

u(ρt) —— F2等级被检砝码密度的不确定度，可从其密度范围7 970～8 030 kg/m3计算得出，认为符合均匀分布

u(ρa) —— 西安地区空气密度不确定度，其计算公式为以下公式：

式中：uF—— 空气密度的近似公式的标准不确定度；

uP—— 实验室大气压力的标准不确定度；

ut—— 实验室温度的标准不确定度；

urh—— 实验室相对湿度的标准不确定度

其中：

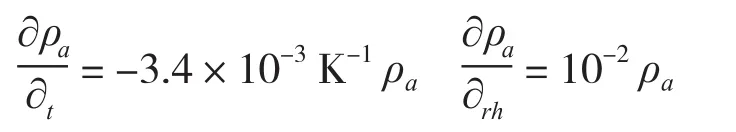
根据气象部门提供的校准证书得出：

则ub的结果见表6。

表6 ub的汇总

5.3.3 空气浮力引起的不确定度由两部分组成，按式（9）进行计算，结果见表7。

表7 u3的评价

5.4 质量比较器分辨力分量引入的不确定度u4的评定

选用的的质量比较器，XP205最大秤量为220 g，实际分度值为0.01 mg；XP26C最大秤量为21 g，实际分度值为1 μg。针对不同的质量比较器，确定其指示器分辨力，按均匀分布，取包含因子计算由此引入的标准不确定度分量u4。计算中数值的引用及计算结果如表8所示，其结果按照式（10）进行计算。

表8 u4的评价

5.5 质量比较器偏载引入的不确定度u5

质量比较器偏载引入的不确定度按照式（11）进行计算

式中：D—— 偏载测量时最大值和最小值之间的差；

d1—— 估计的秤盘中心到砝码中心的距离；

d2—— 秤盘中心到一个角的距离

XP205质量比较仪证书偏载误差D为0.03 mg，估算测量中

XP26C质量比较仪偏载误差D为3 μg，估算测量中

经计算得出结果，如表9所示。

表9 u5的评价

由于质量比较器偏载引起的不确定度分量，已包含在重复性分量的标准不确定度当中，还有现有的质量比较器大多都有定心盘，因此也可以忽略。

5.6 衡量仪器灵敏度引起的不确定度u6

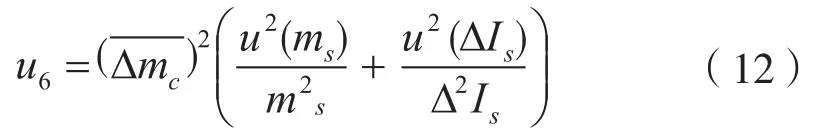
u(ms) —— 灵敏度砝码的不确定度；

ms—— 灵敏度砝码的折算质量值；

ΔIs—— 灵敏度砝码引起的衡量仪器指示值的改变；

u(ΔIs) —— ΔIs的不确定度

由于质量比较仪的精度很高，因此衡量仪器灵敏度引起的不确定度可以忽略。

5.7 砝码磁性引入的不确定度u7

如果砝码极化强度和磁化率满足规程规定的磁性要求，则可认为由于砝码磁性所引起的不确定度分量可忽略不计。

6 合成标准不确定度分析

砝码折算质量修正值测量结果的各项影响因素互不相关，因此其合成标准不确定度按式（13）进行计算，将上面得到的各测量点各分量的计算结果代入，可得到各测量点测量结果的合成标准不确定度，见表10。

表10 uc的评价（单位：mg）

7 扩展不确定度的评定

将表10中得到的各测量点的合成标准不确定度取合适的有效位数，按式（14）计算其扩展不确定度U，记入表11。

表11 U的评价

8 结语

砝码作为计量检定（校准）工作中最常见的计量器具，而且其质量是国际单位制中的基本量，因此其测量结果的不确定度评定尤为重要，希望本文对帮助计量一线人员正确评定砝码校准结果的不确定度有所帮助。

[1]全国法制计量管理计量技术委员会.JJF 1059.1-2012 测量不确定度评定与表示[S].北京：中国质检出版社，2012.

[2]全国质量密度计量技术委员会.JJG 99-2006 砝码计量检定规程[S].北京：中国计量出版社，2006.

[3]肖雯.F2等级砝码测量值的不确定评定[J].计量与测试技术，2017（7）：114.

[4]石红，舒晓莲.计量比对组织与实施中需关注的问题[J].上海计量测试，2016（3）：60-61.

[5]黄坚，苏祎 ， 姚弘，等.质量比较仪校准结果在砝码不确定度评定中的应用[J].计量技术，2017（4）：68-71.