也谈习题变式教学的有效途径

2018-03-21蒋守培

物理教师 2018年2期

蒋守培

(江苏省阜宁中学,江苏阜宁 224400)

习题教学是高中物理教学,特别是高三物理教学的一种重要教学形式,好的习题教学可以提高教学效益,达到事半功倍的效果,更能提升学生的思维品质.本文从提升学生思维品质的角度,对习题变式教学提出几种有效途径,供读者参考.

1 求同思维促进知识的正迁移

在平时的习题教学中,会有大量相同或相似的习题,即便有些表面上不同的东西,其思维方式和解题思路也是相同或相近的.在习题教学中如果能将貌似不同的问题,通过揭示本质,将其归纳在一起,用已有的知识、方法和经验与当前问题情境相联系,用某种固定思维模式去分析问题和解决问题,无疑起到画龙点睛,事半功倍的效果.

下面是某高三复习资料中,“共点力作用下物体的平衡”一份练习上的3道习题.

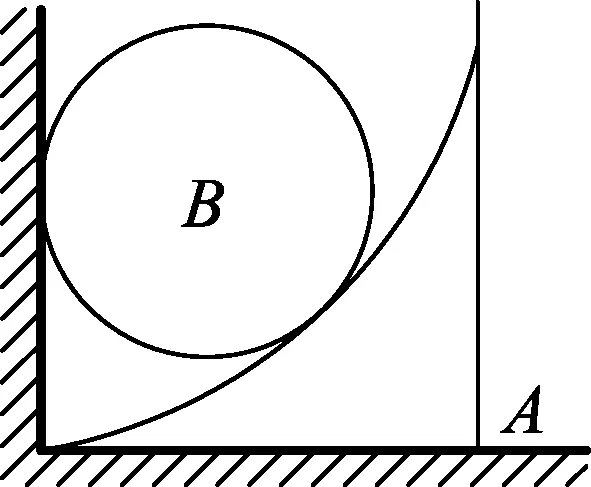
图1

(A) 球B对墙的压力增大.

(B) 物体A与球B之间的作用力减小.

(D) 物体A对地面的压力减小.

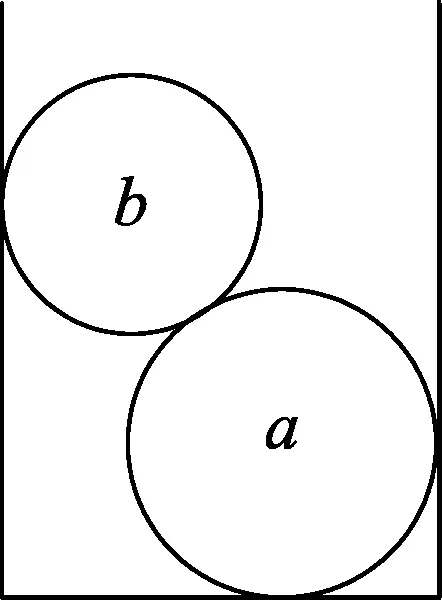
图2

(2) 两刚性球a和b的质量分别为ma和mb,a的直径大于b的直径.现将它们依次放入一竖直放置的平底圆筒内,如图2所示.设a、b两球静止时对圆筒侧面的压力大小分别为F1和F2,筒底所受的压力大小为F.已知重力加速度大小为g.若所有接触面都是光滑的,则

(A)F=(ma+mb)g,F1=F2.

(B)F=(ma+mb)g,F1≠F2.

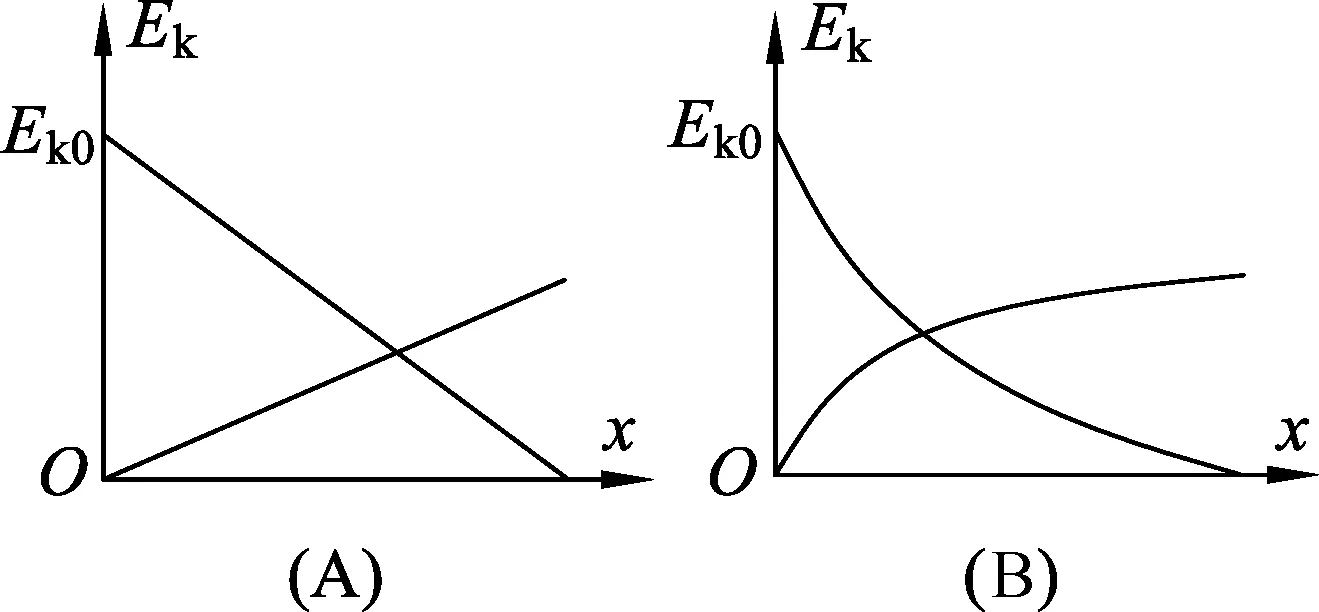
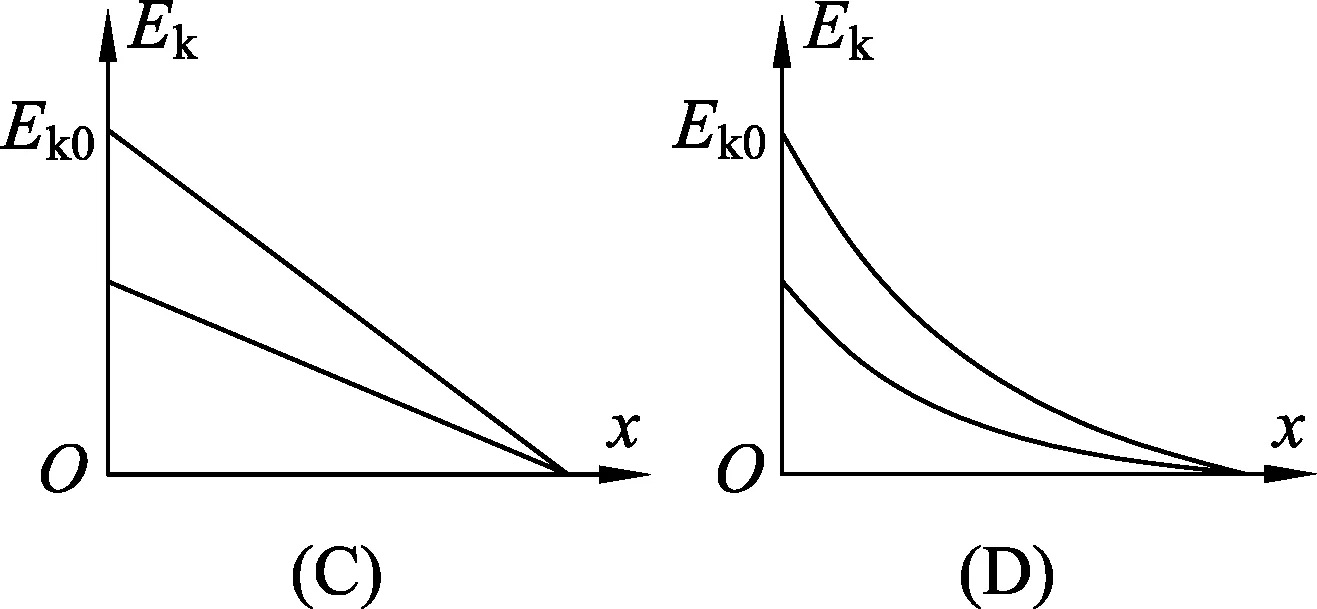
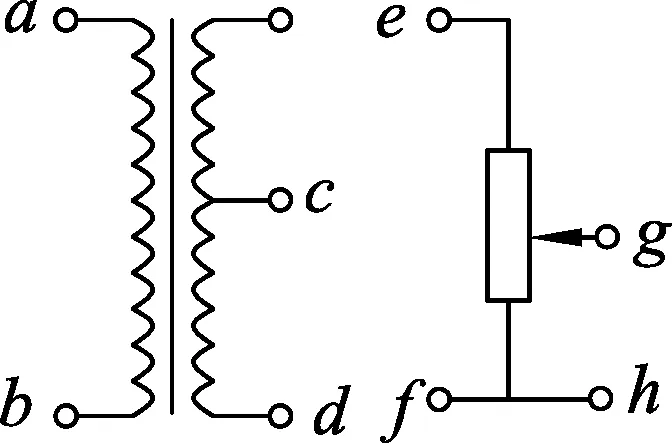
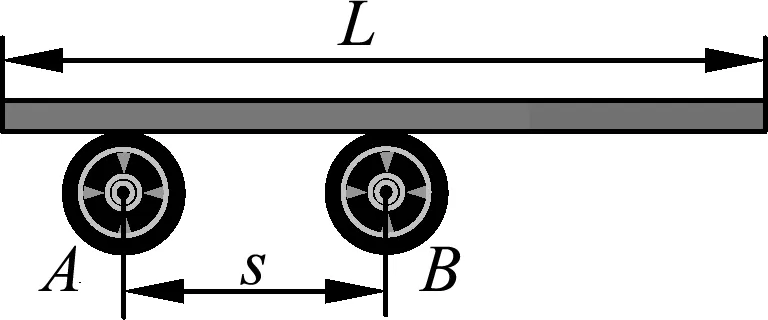
(C)mag

(D)mag

图3

(3) 如图3所示,竖直墙面与水平地面均光滑且绝缘,两个带有同种电荷的小球A、B分别处于竖直墙面和水平地面,且处于同一竖直平面内,若用图示方向的水平推力F作用于小球B,则两球静止于图示位置.如果将小球B向左推动少许,并待两球重新达到平衡时,跟原来的状态相比，

(A) 推力F将增大.

(B) 竖直墙面对小球A的推力变大.

(D) 两小球之间的距离变大.

表面上看这是3道不同情景下的物体平衡问题,但只要对每个物体及整体受力分析后就会发现,它们的受力情景、研究方法、得到的结论完全一样.在讲评这类问题时,只要利用其中1例作为“母题”全面深入地分析清楚,运用求同思维将求解方法正迁移,另外2例也就迎刃而解了.

2 求异思维防止知识的负迁移

求同思维又叫定势思维,它是按照已有的思维模式得到一个确定的解决方案.求同思维对同类问题的解决会起到积极的作用,但过多地强调求同思维会产生一种惰性和教条,当条件发生变化时,由于习惯性思维而陷入困境甚至出现错误.在物理习题教学中,不时地进行求异思维训练,不仅可以使我们习题教学更生动活泼,还能让学生的思维更开放灵活.

下列两例是习题教学中求异思维防止知识负迁移典型的问题.

图4

(1) 如图4所示,两个电路中,当a、b两端与e、f两端分别加上220 V的交流电压时,测得c、d两端与g、h两端的电压均为110 V,若分别在c、d两端与g、h两端加上110 V的交流电压,则a、b与e、f间的电压分别为

(A) 220 V,220 V.

(B) 220 V,110 V.

(D) 220 V,0 V.

本题中两个电路很相似,作用也一样均是改变电压,但它们的原理却不一样,变压器的工作基础是互感,而分压器则是依据串联分压作用,二者存在本质区别.将这两个电路放在一起分析(考查)会使学生有种顿悟的感觉.

图5

(2) 如图5所示,在方向水平的匀强电场中,不可伸长的不导电细线的一端连着一个质量为m的带电小球,另一端固定于O点.把小球拉起直至细线与场强平行,然后无初速释放.已知小球摆到最低点的另一侧,线与竖直方向的最大夹角为θ.求小球经过最低点时细线对小球的拉力.

小球在右端A点释放后,小球在重力、静电力和细线张力作用下沿圆弧做变速圆周运动,研究它的运动过程只能通过动能定理,再利用牛顿第二定律求小球过最低点时细线拉力.在讲评完成后,如果提出:小球在左端B处无初速的释放情况如何呢?定势思维仍会按照原来的套路分析,殊不知小球受力情况发生了改变,细线处于松弛状态,小球在重力和电场力作用下做匀加速直线运动,用牛顿定律和运动学知识讨论(当然也可以用动能定理分析).这样的习题变式拓展学生一定会印象深刻,有一种恍然大悟的感觉.

3 一题多解培养发散思维

一题多解是物理习题教学中常见的一种教学方式,是培养学生发散性思维能力的重要途径.通过一题多解的训练,启发和引导学生从不同的角度、不同的思路,用不同的方法、不同的运算过程去分析、解答同一个问题,使学生摆脱习惯性思维的束缚,产生大量创造性设想,从而使得思维灵活多样.

例如，在平直轨道上甲、乙两物体相距s,同时同向运动.甲以初速度v1,加速度a1做匀加速运动;乙以初速度为0,加速度为a2也做匀加速运动.假定乙在前甲在后,且甲能从乙旁边通过而互不影响,下列情况可能发生的是

(A) 当a1=a2时,甲、乙只能相遇一次.

(B) 当a1>a2时,甲、乙可能相遇两次.

(D) 当a1

本题是运动学中典型追及问题,解法主要有5种. (1) 利用速度关系判断:列出两物体速度、时间关系式,再根据速度大小关系讨论可能相遇的情景; (2) 利用位移关系判断:假设两物体相遇,列出位移等式,通过讨论几个合适的相遇时间,得到可能的相遇次数; (3) 利用相对运动判断:选其中之一为参考系,分析另一物体相对于该物体的运动特点,利用它们相对运动确定相遇次数; (4) 利用v-t图像判断:在同一v-t坐标系中作出两物体的速度-时间图像,利用图像与坐标轴包围的面积关系确定相遇次数; (5) 利用x-t图像判断,在同一x-t坐标系中作出两物体的位移-时间图像,图中可能出现的交点数即为可能相遇的次数.通过这些方法的分析和讨论,可以使学生巩固运动学的基本特点和基本规律,还能促进学生的思维灵活多变.

4 挖掘内涵，完成原题没有完成的问题

物理试题(特别是高考试题)中都包含有丰富内容,由于时间和分值等方面的制约,编写时不可能将同一试题中包含的内容全部挖掘出来让学生解答.这就为讲评该试题留下了拓展延伸的空间.教师在讲评时充分发挥自身的才智,在不改变原有题意的基础上,与学生一起挖掘试题内涵,把命题人想表达但没有表达出来的内容表达出来,让学生的思维来一次飞跃.

图6

(1) 圆柱体边缘上某点的向心加速度;

(2) 圆柱体A、B与木板间的动摩擦因数;

(3) 从开始运动到重心恰在A的上方所需的时间.

这是某市2017年高三调研考试题,该题侧重考查圆柱与长木板间动力学方面的知识,在讲评时完全可以延伸到功能关系的角度来探讨:已知长木板质量m=1 kg,此过程中(1) 摩擦力对长木板做的功; (2) 摩擦力对圆柱体做的功; (3) 系统因摩擦产生的内能等等.这样,本试题的内容就更完整、更丰满,学生对相关的知识的掌握也更系统、更全面.