模型有差异 类比需谨慎
2018-03-21宋辉武
宋辉武 刘 博
(1. 鄂尔多斯市第一中学,内蒙古 鄂尔多斯 017010; 2. 长春师范大学物理学院,吉林 长春 130032)
笔者阅读了本刊2017年第6期一篇论文《2015年高考全国卷Ⅱ第21题评讲有感》,[1]对该文提出的模型迁移很感兴趣,该文将光滑半圆形轨道上质点运动的模型与高考题中的杆连物系的质心运动的模型进行类比,并以此来解释说明杆何时由顶变拉.经过深入思考仔细计算后,笔者发现文中的两个核心观点有失偏颇,实际上文中提到的两种模型形似而神异,作者只关注形式上的相似而忽视神韵上的差异,因此得出了一些经不住推敲的错误结论.


图1 图2
1 图2中质心的运动情况和图1中的质点的运动情况并不相同
首先我们设图1中的质点的质量为2m,图2中的a、b球的质量皆为m,杆长为2l,则我们根据动能定理,对于图1可得
(1)
对于图2可得
(2)
因质心位于杆的中点,因此质心的水平分速度与竖直分速度正好是a、b球的速度的一半(当然质心的水平分加速度与竖直分加速度也是a、b球的加速度的一半),即
(3)
(4)
因此(2)式可改写成
(5)
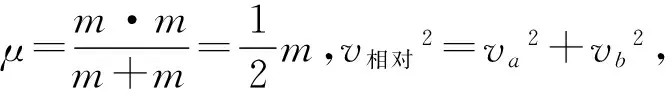
(6)
可以看出(6)式与(2)式是相同的,重力所做的功并不等于质心动能而是等于质心动能加相对动能(此即为柯尼希定理的内容).而图1的模型中重力所做的功全都转化为质点的动能,由此可以看出当图1中的质点与图2中的质心处于相同位置时,二者的速度并不相等,质心的速度必小于质点的速度,也就是说图2中质心的运动情况和图1中的质点的运动情况并不相同.
2 光滑竖直杆对b的弹力与光滑水平面对a的弹力的合力并不是背离圆心或指向圆心

根据质心运动定理可得
(7)
(8)
找到aa和ab的关系也就能够确定Na和Nb的关系,下面我们再来寻找aa和ab的关系.
设Oa长度为x,则x=2lcosθ,两边同时对时间求导得
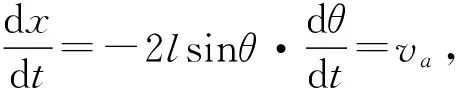
(9)
又vacosθ=vbsinθ,
(10)
则
(11)
将(9)式代入(11)式解得
(12)
(13)
将(7)、(8)两式代入(13)式可得
整理后为
g-ab=aatanθ,
(14)
根据(2)式可得
(15)
将(15)式对时间求导后可得
aa=gcosθ(3sinθ-2),
(16)
由(12)、(14)、(15)式可得
aa=gcosθ(3sinθ-2).
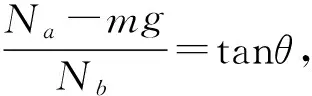
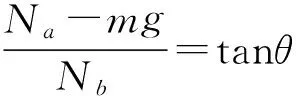
(1) 开始一段时间杆是顶的状态,此时满足Na-mg>0,且Nb>0,物理意义为Na>mg,且Nb方向为水平向右,这个过程中Na-mg与Nb的合力方向是背离圆心的.
(2) 后一段时间杆是拉的状态,此时满足Na-mg<0,且Nb<0,物理意义为Na (3) 临界情况即为杆上的弹力为0,此时杆既不顶也不拉,且满足Na=mg,Nb=0. Na-mg与Nb的合力的变化趋势为:方向先是背离圆心,大小逐渐减小为0,然后方向变为指向圆心,大小由0逐渐增大.Na-mg和Nb的变化趋势同样为逐渐减小到0再反向逐渐增大,即与合力的变化趋势保持一致. 1 唐召军.2015年高考全国卷Ⅱ第21题评讲有感[J].物理教师,2017(6):92-93.
