QC-LDPC码构造及其在BICM-ID系统中的应用*
2018-03-21江梓弘陈晓鹏贺玉成
江梓弘,陈晓鹏,周 林,2,贺玉成,2
(1.华侨大学厦门市移动多媒体通信重点实验室,福建 厦门 361021;2.西安电子科技大学综合业务网理论及关键技术国家重点实验室,陕西 西安 710000)
0 引 言
低密度奇偶校验(Low Density Parity Check,LDPC)码在1962年被首次提出。Gallager在他的文章中定义了LDPC码的概念[1-2],指出它具有稀疏的校验矩阵结构和优异的性能表现,引起了广泛研究。XiaoYu Hu等人提出了PEG(Progressive Edge Growth)算法用于随机构造LDPC码[3],在给定码长、码率和度分布的前提下,通过逐条增加边,获得更大的围长和较少的短环。之后,Tao Tian等人对PEG算法中边的选取方式进行改进,提出了ACE(Approximate Cycle Extrinsic Message Degree)算法[4]。结构化构造法是工程中实用的构造方法。L.Djurdjevic等人发明了一种利用RS码构造QCLDPC码的方法,这种码具有优异的瀑布区性能和很低的错误平层[5]。Shu Lin团队通过有限域方法构造了一系列具有准循环(Quasi-Cyclic,QC)特性的LDPC码[6-7]——QC-LDPC码,能够有效避免短环,具有较好的性能表现,且其校验矩阵拥有准循环的特性,在实际应用中具有很大优势[8]。
编码调制技术方面,1992年Zehavi提出了比特交织编码调制(Bit-Interleaved Coded Modulation,BICM)[9],用于改善衰落信道下的性能表现。该方案中,信息序列在经过编码后进入一比特交织器,之后再进行调制。这样可以分别设计编码器和调制器,灵活性大。同时,由于引入了编码分集增益,使得汉明距离尽量最大化,明显改善了衰落信道下的性能。1998年,Caire等人[10]推导证明了BICM系统抗干扰能力主要是由星座中最小欧氏空间调和均值、最小近邻数以及汉明距离决定的,并完善了BICM系统的理论框架。
1999年,Li等人在BICM的基础上,在解调器和译码器之间引入联合软信息迭代,提出了比特交织迭代译码编码调制(Bit-Interleaved Coded Modulation with Interleaved Decoding,BICM-ID)系统[11],大大改善了系统性能。BICM-ID系统在AWGN、Rayleigh衰落信道下都具有优异的抗干扰能力。理论和实践均表明,将具有强大纠错能力的LDPC码与抗干扰特性强的BICM-ID系统结合,是一种可逼近信道容量的高效编码调制方案。
本文基于有限域构造法,在一定的约束条件下,通过选取两个有限域子集构造QC-LDPC码的基矩阵,保证其Tanner图中的围长至少为6或8,并设计了一种简单有效的掩模矩阵构造法,在矩阵维数较小的情况下,能够获得较大的围长和更少的短环,从而构造出性能优异的QC-LDPC码。然后,将构造的QC-LDPC码与BICM-ID系统相结合,对比文献[12],给出本文构造的各种码在AWGN信道、Rayleigh衰落信道下的误比特率性能,并简单讨论分析解调器和译码器迭代次数对本文系统性能的影响。
1 基于有限域子集的QC-LDPC码构造法
1.1 基矩阵的构造
本文基于文献[13]中的两个定理,利用有限域来构造QC-LDPC码。
定理1:如果矩阵B是QC-LDPC码的基矩阵,且它的校验矩阵H是通过基矩阵B循环移位展开获得的,则该校验矩阵H相应的Tanner图围长最小为6的充分必要条件,是基矩阵B中任取一个2×2大小的子矩阵都是非奇异的或至少包含一个零元素。该约束记为2×2-SM约束。
定理2:如果矩阵B是QC-LDPC码的基矩阵,且它的校验矩阵H是通过基矩阵B循环移位展开获得的,则该校验矩阵H相应的Tanner图围长最小为8的充分必要条件,是基矩阵GF(q)中任取一个2×2或者3×3大小的子矩阵的行列展开式中没有两个相同的非零项。该约束记为3×3-SM约束。
根据上面两个定理,本文利用两个有限域元素的子集来构造QC-LDPC码。在有限域GF(q)设α为本原元。当两个整数k0和n0满足1≤k0,n0<q时,令 S1={αi0,αi1,…,αik0-1}、S2={αj0,αj1,…,αjk0-1}为 GF(q)中的两个元素的子集,其中i,j∈{-1,0,1,…,q-2},且i0<i1<…<ik0-1,j0<j1<…<jn0-1。于是,可构造如下形式的基矩阵B:

将子集S1和S2中的元素分别带入式(1),可得到完整的基矩阵B:
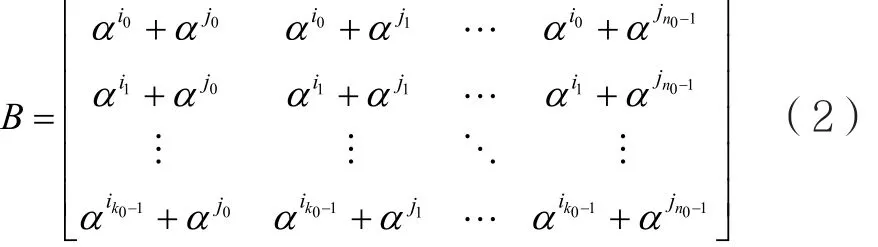
根据上述两个定理,该基矩阵显然满足行列约束条件,则构造出来的码Tanner图围长最少是6。
1.2 掩模矩阵的改进
由有限域构造的QC-LDPC码拥有高度的准循环结构,但因为其中的全零矩阵较少、稀疏性不够,得到的码性能不够优异。为了改善这种情况,采用掩模技术将基矩阵中的一部分非零元素置为0,从而提高校验矩阵稀疏性。传统方法中通常使用PEG生成掩模矩阵。该方法在矩阵较大时能得到较好的性能,但当掩模矩阵较小时,最终得到的码性能往往不佳。针对PEG算法存在的这个缺点,本文根据3×3-SM约束,改进了一种掩模矩阵构造的方法,保证矩阵中任意3×3子矩阵至少有一个零项,使最后得到的码围长至少为8。在掩模矩阵维数较小的情况下,本方法能够很容易地得到具有大围长且性能较好的码。
对于有限域GF(q)中的某个基矩阵B(k0,n0)=[Bi,j]0≤i<k0,0≤j<n0, 设 有 维 数 相 同 的 矩 阵D(k0,n0)=[di,j]0≤i<k0,0≤j<n0,且 D(k0,n0)中的元素只有 0或1。定义如下的运算规则:
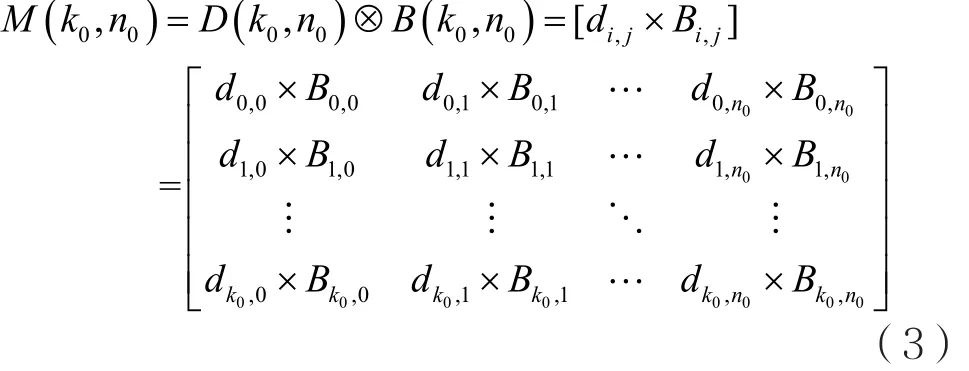
当 di,j=1时,di,j×Bi,j=Bi,j; 当 di,j=0时,di,j×Bi,j=0(全零矩阵)。定义D(k0,n0)为掩模矩阵;M(k0,n0)为掩模生成矩阵。经过这种掩模技术得到的矩阵M(k0,n0)密度较之前的基矩阵B(k0,n0)降低了很多,从而保证了稀疏性。
令两个矩阵y1和y2结构如下:

若基矩阵B(k0,n0)满足k0和n0都是4的整数倍,则可以构造如下形式的掩模矩阵D(k0,n0):

观察掩模矩阵D(k0,n0)易知,经过掩模后生成的矩阵M(k0,n0)的任意3×3大小的子块,最少包含一个零元素,符合3×3-SM约束。因此,它的Tanner图的围长最少是8。
矩阵M(k0,n0)中的每个元素都能够扩展成(q-1)×(q-1)大小的循环置换矩阵A,每个循环置换矩阵A的移位值就是该元素的幂次。将基矩阵B中的所有元素用相应的循环置换矩阵替换,最终便得到校验矩阵H。
2 QC-LDPC码在比特交织迭代译码编码调制系统中的应用
2.1 BICM-ID编码调制系统
BICM-ID系统的基本组成部分如图1所示,由LDPC编码器、交织器、映射器、解映射器、解交织器和LDPC译码器等组成。

图1 BICM-ID系统
将二进制信息序列u=(u0,u1,…,uK-1)输入LDPC编码器中,编码后输出码字序列 b´=(b´0,b´1,…,b´N-1)。将输出的码字序列送入比特交织器进行交织,得到序列 b=(b0,b1,…,bN-1)。将序列 b=(b0,b1,…,bN-1)通过映射器映射到调制信号星座图上,得到信号序列s。调制后的信号s通过信道时会存在一些噪声影响,因此最后接收端获得的信息y为:

其中,ρ为Rayleigh衰落的衰落因子,且E(ρ2)=1;n是复高斯白噪声,它的平均值为0,方差是σ2=N0/2ES;ES是信道符号能量,N0是单边噪声功率谱密度。在AWGN信道中,ρ=1。
接收端收到受到噪声干扰的信号y后,进行一系列处理,得到最终的译码判决结果u-。接收端的解映射器和译码器间采用联合迭代的方式译码。解映射器通过接收信号y和先验对数似然比,计算解映射器的比特级对数似然比外信息序列,其再经过解交织器后得到序列LDa作为译码器输入;译码器译码后输出外信息序列LDe,经交织后反馈回解映射器,作为下一次迭代的先验对数似然比LMa,然后重新变为先验信息送进解调器开始下一轮的迭代更新,以增加信息来源的可靠性。初次迭代时,LMa=0。通过反向交织器,译码器和解调器之间的信息在每一轮迭代时进行传递,增加外赋信息的准确性,从而最终降低错误概率。
2.2 解调译码方法
软信息迭代更新在解调和译码两个模块之间进行。假设进行第t次外部迭代时,对每个比特其先验信息是相互独立的。若从信道接收到的信号符号为yk,c表示对应比特序列,L表示比特序列的长度,则解调器的外赋信息可由式(7)计算得到:

译码器采用BP译码算法,具体步骤如下:
(1)初始化。初次迭代次数k=1,对全部的变量节点vn,计算初始的信道LLR值Lch,n;设是某个校验节点cm输出的,令Lch,n。
(2)计算校验节点。对校验节点集合B(m)中的某个cm,变量节点vn输出信息。
(3)计算变量节点。在第k次迭代中,vn更新后验LLR值和cm输出。
把该序列和校验矩阵的转置HT做乘法,获得伴随式Sk。若Sk=0,则译码正确,直接输出判决后的序列;若Sk≠0,则译码不正确,迭代次数加1,开始新一轮的迭代,直到Sk=0。若达到预先设定的迭代次数时Sk≠0,则译码失败。
2.3 仿真结果
本文搭建BICM-ID系统模型,采用本文构造的(1 524,762)和(4 088,2 044)QC-LDPC码作为信道编码,与文献[12]中由PEG算法构造的(5 310,2 655)非规则LDPC码进行性能对比,结果如图2所示。本仿真在AWGN信道下进行,LDPC译码器最大内迭代次数设为20次,外迭代次数设为1次,调制方式为16-QAM和64-QAM,星座图均采用Gray映射,LDPC译码器采用标准和积译码算法。
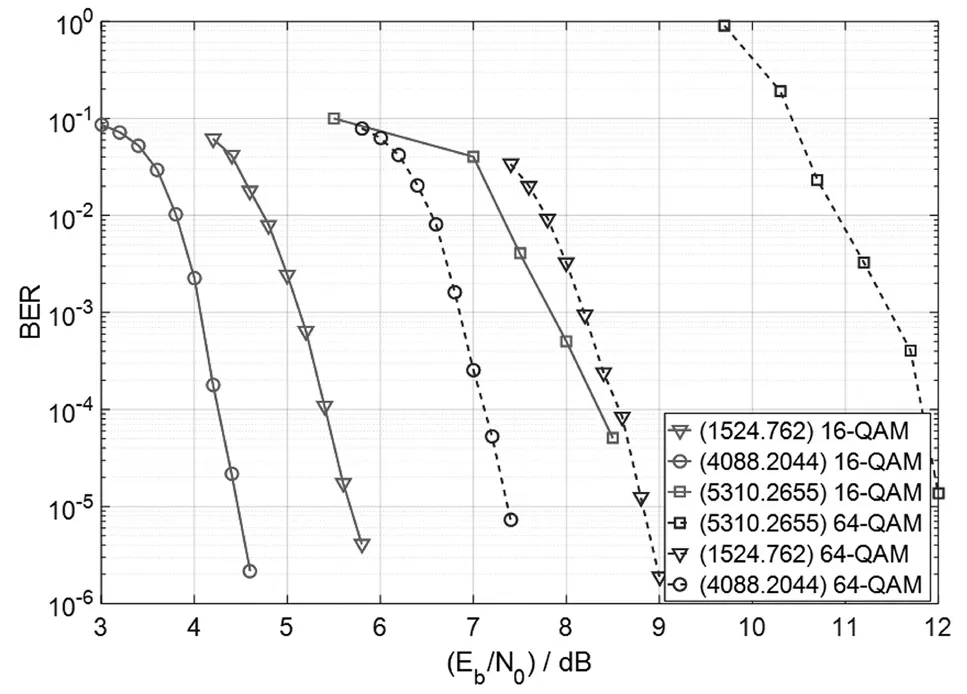
图2 AWGN信道下误码率曲线对比
如图2所示,本文构造的QC-LDPC码误码率性能表现更加优异,(1 524,762)和(4 088,2 044)QC-LDPC码对比(5 310,2 655)非规则LDPC码,在16-QAM调制下,当误码率达到10-4时,前者性能改善约3 dB,后者性能改善约4 dB;在64-QAM调制下,当误码率达到10-5时,前者性能改善约3.2 dB,后者性能改善约4.5 dB。
采用本文构造的(1 524,762)和(4 088,2 044)两种QC-LDPC码,结合QPSK、16-QAM和64-QAM三种调制方式,在Rayleigh衰落信道下进行仿真。LDPC译码器最大内迭代次数设为10次,外迭代次数设为5次,采用和积译码算法,其性能表现如图3所示。可以看出,在Rayleigh衰落信道下,本文构造的QC-LDPC码有着优异的BER性能,且随着码长的增加,其抗衰落性能有更大的改善。

图3 Rayleigh衰落信道下不同调制方式的误码率曲线对比
采用本文构造(1 524,762)和(4 088,2 044)两种QC-LDPC码,结合16-QAM调制方式,在Rayleigh衰落信道下进行仿真。LDPC译码器最大内迭代次数分别设为10次和30次,外迭代次数分别设为1次、5次,采用和积译码算法,其性能表现如图4所示。可以看出,码长和码率不变的情况下,最大内迭代次数不变,随着外迭代次数的增加,误码率性能提高。同理,外迭代次数不变,随着最大内迭代次数的增加,误码率性能提高。究其原因,在于增加LDPC码译码的内部迭代次数,使得LDPC码的译码算法产生的外信息可靠性提高,从而有效减少了错误传播,且通过增加解调器与LDPC码之间信息交换进行的外部迭代次数,能够进一步提高系统性能。

图4 Rayleigh衰落信道下不同迭代次数的误码率曲线对比
3 结 语
本文在有限域基础上,设计了一种基于有限域子集的QC-LDPC码构造方法,同时针对PEG算法在构造维数较小的掩模矩阵时最终获得的码性能不好的缺陷,改进了一种简单有效的掩模矩阵构造法。在BICM-ID系统的基础上,结合几种调制方式,得到了不同码长的QC-LDPC码在不同信道下的误码率曲线。仿真结果表明,本文构造的QC-LDPC码在AWGN信道和Rayleigh衰落信道下的误码率性能表现优异。它在AWGN信道下通过不同调制方式,表现的误码率性能均优于传统方法。当误码率达到10-5时,最大性能改善达4.5 dB。此外,QC-LDPC码的校验矩阵拥有准循环特性,在实际应用中具有明显优势。
[1] Gallager R G.Low-density Parity-check Codes[J].IEE Trans. Inform. Theory,1962(08):21-28.
[2] Gallager R G.Low-Density Parity-Check Codes[D].Cambridge MA:MIT Press,1963.
[3] Hu X Y,Eleftheriou E,Arnold D M.Progressive Edge-growth Tanner Graphs[C].Proc. IEEE Globecom,2001:995-1001.
[4] Tian T,Jones C,Villasenor J D.Selective Avoidance of Cycles in Irregular LDPC Code Construction[J].IEEE Trans. Commun.,2004:1242-1247.
[5] Djurdjevic J X,Abdel-Ghaffar K.A Class of Low-density Parity-check Codes Constructed Based on Reed-Solomon Codes with Two Information Symbols[J].IEEE Commun. Lett.,2003,7(07):317-319.
[6] Lan L,Zeng L Q,Tai Y Y.Construction of Quasi-cyclic LDPC Codes for AWGN and Binary Erasure Channels:A Finite Field Approach[J].IEEE Trans. Inform.Theory,2007,53(07):2429-2458.
[7] Kou Y,Lin S,Fossorier M P C.Low-density Parity-check Codes Based on Finite Geometries:A Rediscovery and New Results[J].IEEE Trans. Inform. Theory,2001(47):2711-2736.
[8] Xu H,Feng D,Luo R.Construction of Quasi-Cyclic LDPC Codes via Masking with Successive Cycle Elimination[J].IEEE Commun.Lett.,2016,20(12):2370-2373.
[9] Zehavi E.8-PSK Trellis Codes for a Rayleigh Channel[J].IEEE Trans. Commun.,1992,40(05):873-884.
[10] Caire G,Taricco G,Biglieri E.Bit-interleaved Coded Modulation[J].IEEE Trans. Inform. Theory,1998,44(03):927-946.
[11] Li X,Ritcey J A.Bit-interleaved Coded Modulation with Iterative Decoding[C].Proc. IEEE International Conference on Communications(ICC),1999(02):858-863.
[12] 顾品标,吴乐男.迭代译码的LDPC-BICM方案在中短波信道中性能分析[J].信号处理,2014,30(01):30-36.GU Pin-biao,WU Le-nan.The Performance of Iterative Decoding Schemes based LDPC-BICM in MF and HF Channels[J].Journal of Signal Processing,2014,30(01):30-36.
[13] Li J,Lin S,Abdel-Ghaffar K.Algebraic Quasi-cyclic LDPC Codes:Construction,Low Error-floor,Large Girth and a Reduced-complexity Decoding Scheme[J].IEEE Trans. Commun.,2014,62(08):2626-2637.
