一种改进的认知无线电信号检测方法研究
2018-03-21陈通,熊刚
陈 通,熊 刚
(中国电子科技集团第三十研究所,四川 成都 610041)
0 引 言
随着无线通信技术的迅猛发展,可用的频谱资源日益缺乏。目前,一些固定频段分配技术使通信系统的容量和灵活性受到局限,且容易导致干扰。由此,认知无线电技术作为一种能够自动感知周围无线环境、实时调节信号参数的智能通信系统应运而生。对于认知无线电系统,在不干扰主用户的前提下,其他用户可动态检测和利用空闲频谱信号,理论上容许进行多维复用,提高了频率资源的利用效率。认知无线电在民用和军事领域都具有广泛的应用前景和重要研究意义[1],如超宽带(UWB)通信系统、无人机智能数据链、物联网传感系统等。从2005年到现在,美国研究机构通过国防部资助,已顺利实现了XG计划、GEMSIS、WNaN计划等重点项目,奠定了良好的技术基础;欧盟在移动通信方面成功实施了DRIVE、OverDRiVE和TRUST等认知无线网络项目研究,取得一些进展;近年来,我国在863计划和973计划的支持下,开始对认知无线电网络系统的空间信号检测和分析、合作和跨层设计技术以及QoS保证机制等方面进行深入研究,受到了研究人员越来越多的关注。
认知无线电需要具备频谱感知能力,从而检测并获取到可用频段中的频谱资源,在不影响原授权用户的情况下,实现认知用户的正确通信。信号频谱检测技术是认知无线电系统中的一项关键技术,有助于感知周围电磁环境中是否存在空闲频率,并能检测出新用户是否接入该频段,确保二级用户实时、合理地使用和退出,提高通信频谱效率[2]。随着认知无线电和动态频谱接入技术的进一步发展,认知无线电信号检测已逐步成为研究热点。学者们在过去提出了一些认知无线电信号的检测思路,一般可分为三大类:基于发射机的检测、基于接收机的检测和基于干扰检测的思路。目前,使用较广泛的是基于发射机的检测思路,属于非合作式检测,应用范围比其他思路更广泛。此外,基于匹配滤波器的检测算法的缺点在于需要事先取得主用户信号特征信息,且对相位同步要求高,否则性能将受到很大影响。能量检测算法虽然无需先验知识,但在低信噪比下的性能较差,且由于噪声的不确定性,其检测门限难以确定。基于静态循环谱特征检测的算法缺点是计算量大、处理时间长,满足实时性要求较困难。
针对以上问题,本文提出了一种适用于认知无线电信号检测的新改进方法。该方法首先采用基于能量检测的思路进行初判决,其次根据预判进一步分析信号的相关性特征,并通过自适应动态门限达到最终正确检测的结果。该算法利用信号的相关系数特征,可以增强算法的抗噪性能;在处理中进行优化,比过去一些基于信号相关和循环谱检测思路的运算量更小,使得算法具有良好的工程实用性。
仿真结果表明,本文的改进算法在低信噪比条件下能够达到较高的正确检测概率,相比传统的能量检测算法性能更优。
1 传统的信号检测模型
信号检测技术的传统思路是采取能量检测法,这对于认知无线电信号判识也适用。在非合作情况下,信号检测算法设计中的一个难点是实现低信噪比条件的准确判断。认知无线电信号检测可表示为如下的二元假设检验模型:

其中t表示采样点序号,M表示观测时间内收集的采样点数,s(t)表示主用户发射信号,是独立同分布的随机过程。n(t)表示高斯白噪声,是独立同分布的高斯随机过程,其方差为σn2,均值为0。h(t)表示待检测频段的信道响应,x(t)表示认知用户的接收信号。假设频谱感知时间小于信道响应的持续时间,且信道增益在该段时间内基本不变,由此h(t)可视为常量h。
模型假设H0表示待检测频段中的主用户信号不存在,假设H1代表该频段中存在有主用户信号。设认知节点收集了M个接收信号采样点,而信号能量检测的计算式可表示如下:


其中n表示时间-带宽乘积,η表示信噪比。在低信噪比情况下,为了满足一定的性能,M的值通常很大。所以,可以采用中心极限定理将检验统计量近似为高斯量:
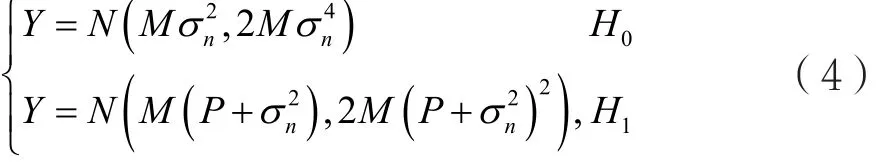
其中P表示主用户的平均信号功率,然后预警概率Pfa和检测概率Pd为:

其中Q(·)表示标准的高斯复数累积分布函数,且Pfa表示判决门限。根据常虚警率(CFAR)定理,在认知无线电系统中,判决门限应设置为满足一定的虚警概率Pfa。γ可由式(7)给出:

2 算法分析和改进
传统的能量检测算法极易受到噪声的影响,在低信噪比情况下,一般较难区分噪声和主用户信号。因此,为了减少信噪比因素对算法性能的影响,本文算法引入了基于信号相关性特征的判断思路,并采用动态检测门限以提高检测概率。根据式(5)和式(6),如果能够对主用户信号进行预判决,则可以合理调整门限达到最优,由此提高检测概率,减小虚警概率。
本文提出了一种基于能量检测与信号相关性特征结合的认知无线电信号检测算法。因为短时间内认知无线电主用户信号状态不会发生较大变化,所以在一段连续时间内统计的主用户信号能量可被划分为L部分,且在不同时间段内对能量Y(x)(i)(1≤i≤L)进行计算。时长L内的能量均值可表示为:

算法处理中,可对主用户信号存在状态进行预判,即如果Y(x)avg≥γ,则判断H1成立,表示主用户信号可能存在;如果Y(x)avg<γ,则判断H0成立,结论相反。
与基于循环谱的检测算法不同,本文改进方法综合考虑了计算量因素,不需进行复杂的循环谱计算求取过程。由于主用户信号之间相关性与高斯白噪声的不同,可引入相关系数ρ进行计算分析,进一步实现最终的判决。
在时长L内的不同时间段,能量可以用式(9)表示:

信号采样点相关运算的均方差矩阵可表示为:

接下来在矩阵S的所有特征值集合内进行搜索,求出相关特征值的最大值和均值。相关系数可由式(11)进行计算:

若经过预判决处γ理后认为H1假设成立,动态检测门限可用进行计算;若经过预判决处理后认为H0假设成立,动态检测门限可用γdyn2=γρ进行计算,即:


下面对新改进算法处理步骤进行归纳说明。
(1)将一段时间内的待测信号输入检测算法模型,该段观测时间划分为L部分,并计算不同时间段的信号能量Y(x)(i)(1≤i≤L),然后再计算能量Y(x)(i)的均值 Y(x)avg;
(2)基于能量检测思路进行预判决,比较Y(x)avg和门限γ的值,若Y(x)avg≥γ,则H1成立,可初步判断信号存在;若Y(x)avg<γ,则H0成立,结论相反;
(3)采用动态门限的优化思路实现进一步检测。计算Y(x)(i)的相关性均方差矩阵,求取特征值
最终,可通过比较Y(x)L和γdyn,判断主用户信号是否存在,即:从而得出不同情况下的检测门限,如式(12)所示。
3 仿真结果及性能分析
为了验证本文方法的有效性,进行了下面的算法仿真实验。主用户信号采用BPSK调制方式,采样率为800 kHz,载波频率为200 kHz,码速率为50 kb/s,信号采样点长度为4 096,信道为高斯白噪声信道,Monte-Carlo仿真次数为1 000次。
仿真实验1:仿真参数如前所述,对不同信号累积长度L=10、15、20且不同信噪比情况下的算法性能进行分析。如图1所示,其中横轴表示检测概率Pd,纵轴表示信噪比SNR。

图1 本文方法对不同长度信号正确检测率曲线
从图1可以看出,信号的累积长度L越大,算法的性能越优,当L=20时,信号检测正确率最高。但在工程实际中需综合考虑计算复杂度等因素,所以一般可选取信号累积长度L=15,可满足低信噪比条件下的检测需求。
仿真实验2:仿真参数如前所述,对传统的基于能量检测方法和本文新改进方法进行仿真验证,结果如图2所示。
从图2可以看出,相比传统的能量检测方法,本文的改进方法检测性能更优。
4 结 语
认知无线电系统的目标是实现信号频谱的高效利用和自适应传输,具有巨大的发展前景。本文提出了一种对认知无线电信号检测的改进方法,将能量检测与基于相关性特征的算法进行融合,从而增强了抗噪性能和门限判决的适应性。仿真实验表明,和过去传统的一些方法相比,新方法可以提高检测性能,并该方法综合考虑了计算量因素,工程实用性较强。今后可进一步优化,为解决低信噪比的复杂环境中认知无线电信号检测问题提供一种更有效的手段,还可应用于电磁环境监测、通信对抗等领域。

图2 各方法的正确检测率对比曲线
[1] 白敏丹.基于认知无线电的无线通信研究现状[J].通信技术,2010,43(05):45-49.BAI Min-dan.Situation of Wireless Communication Research on Cognitive Radio[J].Communications Technology,2010,43(05):45-49.
[2] 刘元,彭端,陈楚.认知无线电的关键技术和应用研究[J].通信技术,2007,40(07):50-52.LIU Yuan,PENG Duan,CHEN Chu.Investigation on the Key Techniques and Applications of Cognitive Radio[J].Communications Technology,2010,40(07):50-52.
[3] Ramkumar B.Automatic Modulation Classification and Blind Equalization for Cognitive Radios[D].Virginia:Virginia Polytechnic Institute and State University,2011.
[4] Li B,Sun M W,Li X F,et al.Energy Detection Based Spectrum Sensing for Cognitive Radios over Time Frequency Doubly Selective Fading Channels[J].IEEE Transactions on Signal Processing,2015,63(02):402-417.
[5] JaisinghL R,Dey D K,Griffith W S.Properties of a Multivariate Survival Distribution Generated by a Weibull and Inverse-Gaussian Mixture[J].Scandinavian Journal of Statistics,1993,42(04):618-622.
