基于Gevers-Wouters算法的ARMA模型改进
2018-03-21唐欣欣邓光明
唐欣欣,邓光明,b
(桂林理工大学a.理学院;b.应用统计研究所,广西桂林541006)
0 引言
在时间序列分析中,一般会假设认为某一变量的未来值能够完全由该变量的现在和过去值预测,而不受到其他变量的影响。由于这个假设很强,通常不能完全满足,所以误差是不可避免的。例如对于平稳的时间序列会构造ARMA模型对数据进行拟合,但是往往拟合的效果并不能达到预期,为了能提高预测的准确性,这个时候就要通过一些特殊的统计方法对ARMA模型进行进一步的改进。
目前在改进ARMA模型方面已经有很多研究,有学者将ARMA模型与其他的模型相结合,吴朝阳[1]基于灰色GM(1,1)模型和ARMA模型得到组合模型GM-ARMA模型减小了误差,邵龙锋[2]把小波变换的思想引入到ARMA模型中对其进行改进而后预测,任强等[3]用Leslie矩阵和ARMA模型得到人口随机预测方法。同时也有学者在已构造的ARMA模型基础上,通过调整各项参数达到提高预测精度的目的,何永沛[4]结合优化理论中的阻尼最小二乘法求解ARMA模型参数并在预测性能上有了较大的提高,黄雁勇等[5]通过DFP算法构造具有遗传对称正定性的矩阵来近似Hesse矩阵的逆从而实现ARMA模型的参数估计,孙汝儒等[6]提出用改进的PSO算法对ARMA(r,m)模型定阶的新方法。
本文以我国国内航线的旅客周转量为例,考虑到航空客运行业会因为节假、气候等因素出现市场波动,需要一种精度较高的时间序列短期预测模型进行拟合,所以在剔除了季节趋势之后用ARMA模型解决这类时间序列建模的问题。但是由于预测的误差较大,为提高精度引入了Gevers-Wouters算法调整模型的参数,以此达到改进模型的目的。
1 理论基础
观测到的时间序列用{Yt}表示,并用{et}表示未观测到的白噪声序列(即一列均值为零的独立同分布的随机变量)。
一般线性过程{Yt}可以表示为现在与过去白噪声变量的一种加权线性组合,如公式(1)所示:
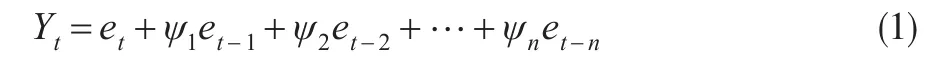
如果公式(1)的右侧是一个无穷级数,为了让表达式具有数学意义,则需要对权数ψ做出如下假设:

因为{et}是无法观测到的白噪声序列,所以假设et的系数为1不会导致公式(2)失去一般性,即ψ0=1[7]。
当有限个系数ψ不为零的时候,得到移动平均过程,写成公式(3)的形式:
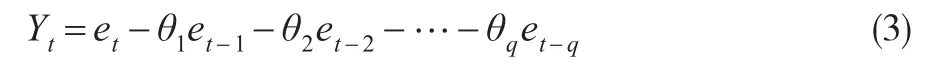
公式(3)被称之为q阶移动平均过程,简单记为MA(q)。
以自身做为回归变量的过程称之为自回归过程,记为AR(p),即序列Yt的当期值是自身最近p阶滞后项和新信息项et的线性组合,由此得到p阶自回归过程写为公式(4)的形式:
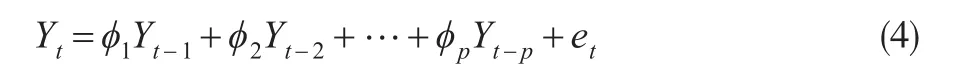
其中,et包括了序列在t期无法用过去数值来解释的所有新信息。对于每一个时期,假设et独立于Yt-1,Yt-2,Yt-3,…。
如果假定序列中部分为自回归过程,部分为滑动平均过程,由此就可以得到一个很普遍的时间序列模型,自回归移动平均过程,用公式(5)表示如下:
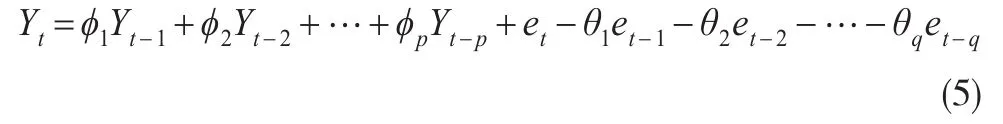
可以简单记为ARMA(p,q)。这种情况下,时刻t系统值Yt不仅和以前时刻的序列值相关,而且同以前时刻进入系统的扰动项也存在着一定的依存关系[8]。
2 数据来源及预处理
本文从2010年1月至2016年3月的中国民航主要运输生产指标统计获取国内航线的旅客周转量x1(单位:万人·公里),绘制出时序图,如图1所示。
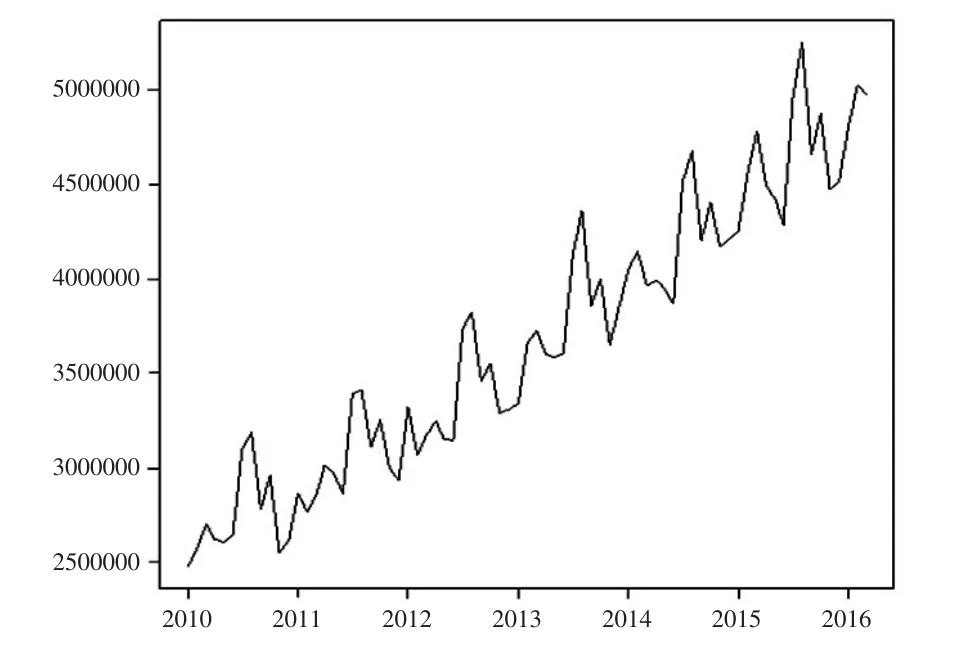
图1 国内航线旅客周转量时序图
从图1可以看出,我国国内航线的旅客周转量自2010年以来呈现出稳步上升的趋势,不可忽视的是,其中伴随着一定的季节波动。导致季节变动的原因是多种多样的,譬如气候、节假日等都是使时间序列发生规律性变动的因素。通过季节调整,消除序列中的季节性影响,能够更清晰地揭示趋势。为了可以更加准确地反映客观经济的本质属性,就需要对时间序列中的季节变动因素采取一定消除和调整的方法。为了能够准确地构建时间序列模型,需要剔除掉数据中的季节趋势部分。基于Loess方法对旅客周转量数据做季节趋势分解,得到三个部分,如图2所示,自上而下分别是趋势、季节以及冗余。
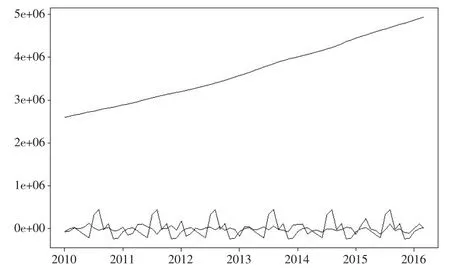
图2 国内航线旅客周转量的趋势分解图
输出季节部分的数据,各月季节波动的数据如表1所示。从表1中可以看出,在每年的8月份左右达到一个明显的高峰,在11月份左右产生低谷。了解了国内航线旅客周转量的基本趋势之后,需要进一步拟合曲线才能有效预测未来发展趋势。
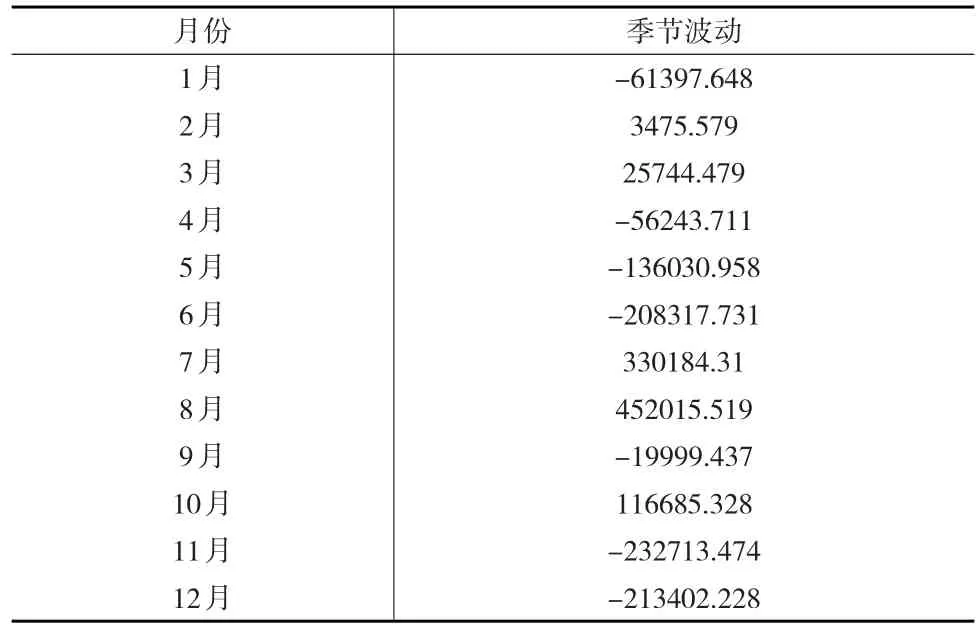
表1 各月季节变化情况
首先需要去除季节变动成分,将剩余部分的数据取对数后进行ADF检验。ADF检验显著性水平为0.01,0.05和0.1的临界值分别是-4.04,-3.45,-3.15(值越小越显著)。该数据的检验统计量为-6.5804,在显著性水平为0.01、0.05和0.1时均小于临界值,说明这组对数序列是平稳的。所以可以直接对这组对数数据构建ARMA模型。
3 构建ARMA模型
构建ARMA模型一般情况下是输出acf和pacf这两个条形图用以判断阶数,但是这样的判断带有一定的主观性而且很多时候阶数并不容易看出。所以,本文用R软件程序包TSA中的函数armasubsets()根据BIC准则来判断阶数。
本文将最大的p和q均设置为14,对于不同的p和q会显示出对应的BIC值。BIC是从贝叶斯的角度发展而来,近似于要求后验模型的概率最大,而先验模型在所有模型中有均匀的分布[9]。
BIC(贝叶斯信息量)的表达公式如下:

其中,L表示的是最大似然,n表示的是数据数量,k表示模型中的变量个数。
去除季节变动的国内航线旅客周转量At拟合的时间序列模型如公式(7)所示:

确定时间序列模型的阶数后,可通过Ljung-Box检验了解模型的拟合情况。
Ljung-Box检验的零假设是对于某个滞后序列独立,其p值小说明可能有相关性,而对于不相关的观测值(如:纯随机过程)p值则应该很大。对数据的残差做Ljung-Box检验,并将检验得到的p值做出点图,如图3所示。
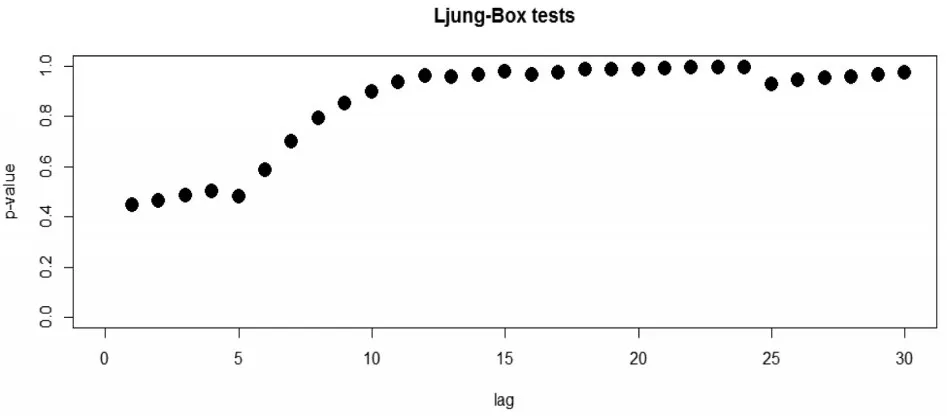
图3 数据残差的Ljung-Box检验的p值
从图3可以看出,在滞后1~5的Ljung-Box检验的p值较小,这个滞后范围看不出显著的不相关性,但是对较长滞后(5~30)做检验p值呈现出不断增大的趋势并接近于1。对于所有的滞后阶数p值均大于0.05这一水平,因此不能够拒绝原假设,即数据的残差不存在相关性[10]。所以,可以用公式(7)这个模型对国内航线旅客周转量的情况进行预测。
通过构造的时间序列模型预测2016年4月至2017年3月lnAt的值,并绘制出时序图,如图4所示。
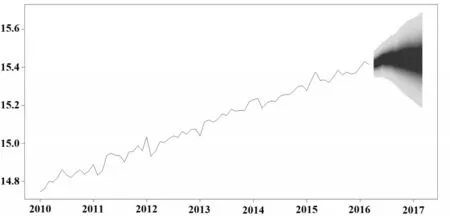
图4 ARMA模型预测图
图4标出了误差允许范围内的旅客运输周转量预测区间。在此基础上,加上各月季节变动量(见表1)求出旅客周转量预测值,即得到未来十二个月我国民航旅客运输周转量,如表2所示。目前中国民用航空局最新的数据公布为2016年4月的中国民航主要生产指标,通过与真实值比较可以发现,误差值为1.82%,该模型预测的误差还是较大的。为提高预测的精度,还需要对模型进行进一步的改进。
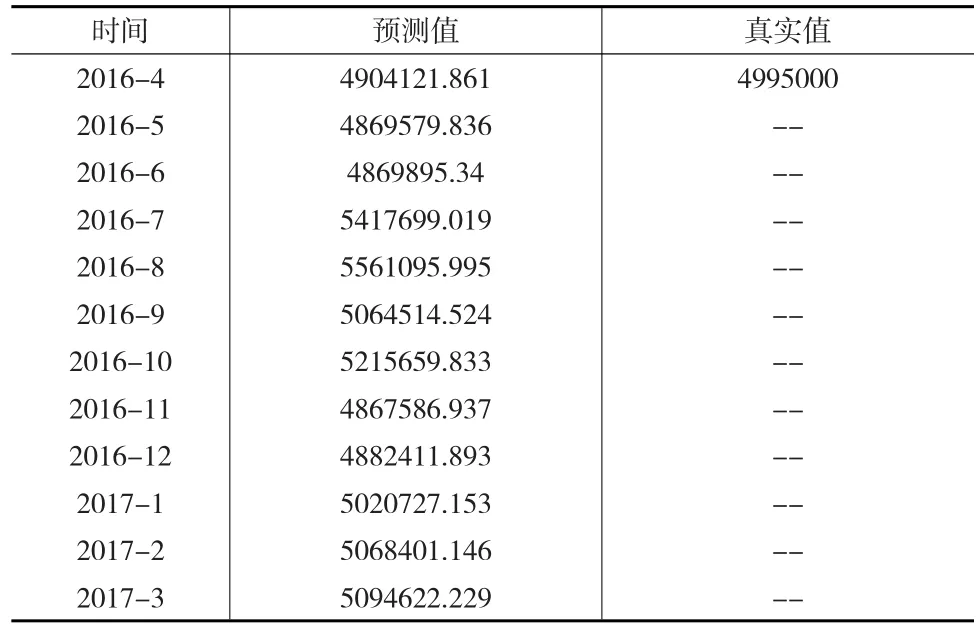
表2 旅客周转量预测值和真实值之间的比较
4 模型的改进
模型改进的目标主要是对国内航线构造的ARMA模型的参数进行合理的调整,由此引入ARMA新息模型的概念。ARMA新息模型是现代时间序列分析方法的基本工具,它是观测信号的ARMA模型。基于ARMA新息模型,可以把最优滤波问题转化为由新息序列生成的线性空间中的射影问题[11]。构造ARMA新息模型的关键就是构造其MA(移动平均过程)部分。
估计MA部分的参数用到了Gevers-Wouters算法[12]。
用r(t)表示m维的移动平均模型MA(n):
该试验选择在水稻成熟期(10月末)展开植株采样和水稻经济性状测试,专门对水稻的株高、有效穗、每穗实粒数、结实率以及千粒重进行对比分析。实验中采用了烘干法进行产量折算,最后对水稻生产的经济效益进行了精确评估。

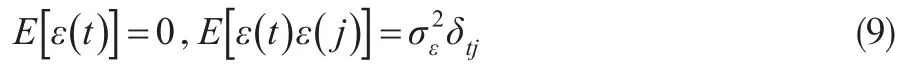
设初始时刻t0=-∞,则r(t)是一个平稳随机序列。已知r(t)的阶次nd和相关函数:
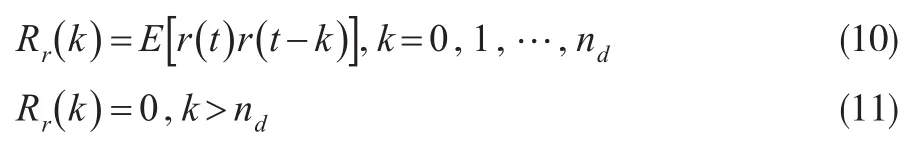
由Rr(k)求MA参数d1,…,dnd和[13]。
考虑可逆的纯量MA(nd)过程即公式(8),已知其相关函数Rr(k),k=0,1,…,nd,则可用Gevers-Wouters迭代算法求MA参数di和:
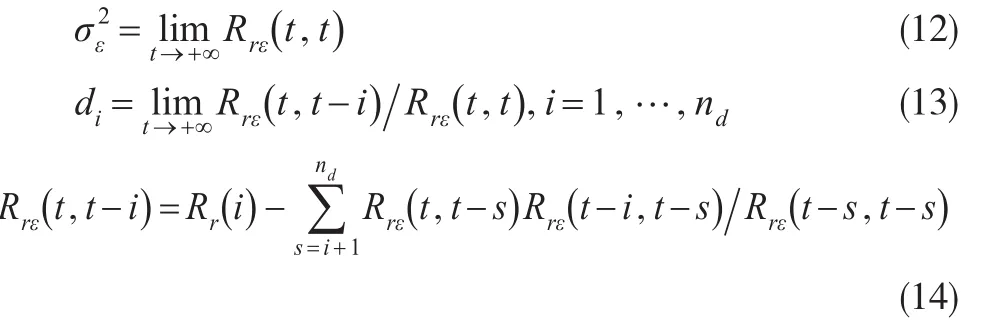
其中t=0,1,2,…,i=t,t-1,…,0且规定:
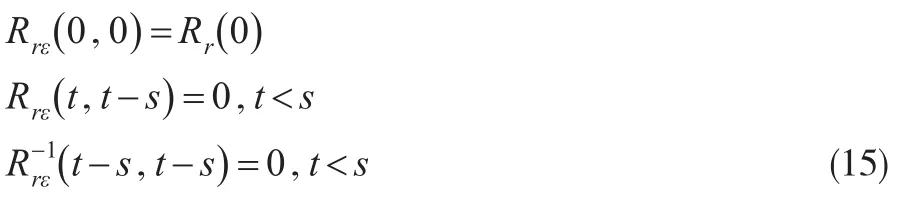
在较弱的情况下,上述的极限关系是成立的,并且可以保证MA(nd)过程是可逆的。应用上述Gevers-Wouters算法,取迭代次数t充分大,则在时刻t时有估值:

通过迭代次数t=50~100便可以达到参数估计误差不超过10-3的满意精度。
将上述单变量MA参数估计的Gevers-Wouters算法推广到多变量的情形,考虑可逆的多变量MA过程:

其中r(t)∈Rm,ε(t)∈Rm是零均值、方差阵为Qε的白噪声,q-1为单位滞后算子,且多项式矩阵D(q-1)=Im+D1q-1+…+Dndq-nd是稳定的(即detD(x)的零点全位于单位圆外)。记它的相关函数为Rr(i)=E[r(t) rT(t-i)],i=1,…,nd;Rr(i)=0(i>nd)。
将构造的国内航线旅客周转量ARMA(6,7)模型中移动平均过程单独提取出来,通过Gevers-Wouters算法重新估计参数。画出t=1~100时MA的各项参数估值,如图5所示。
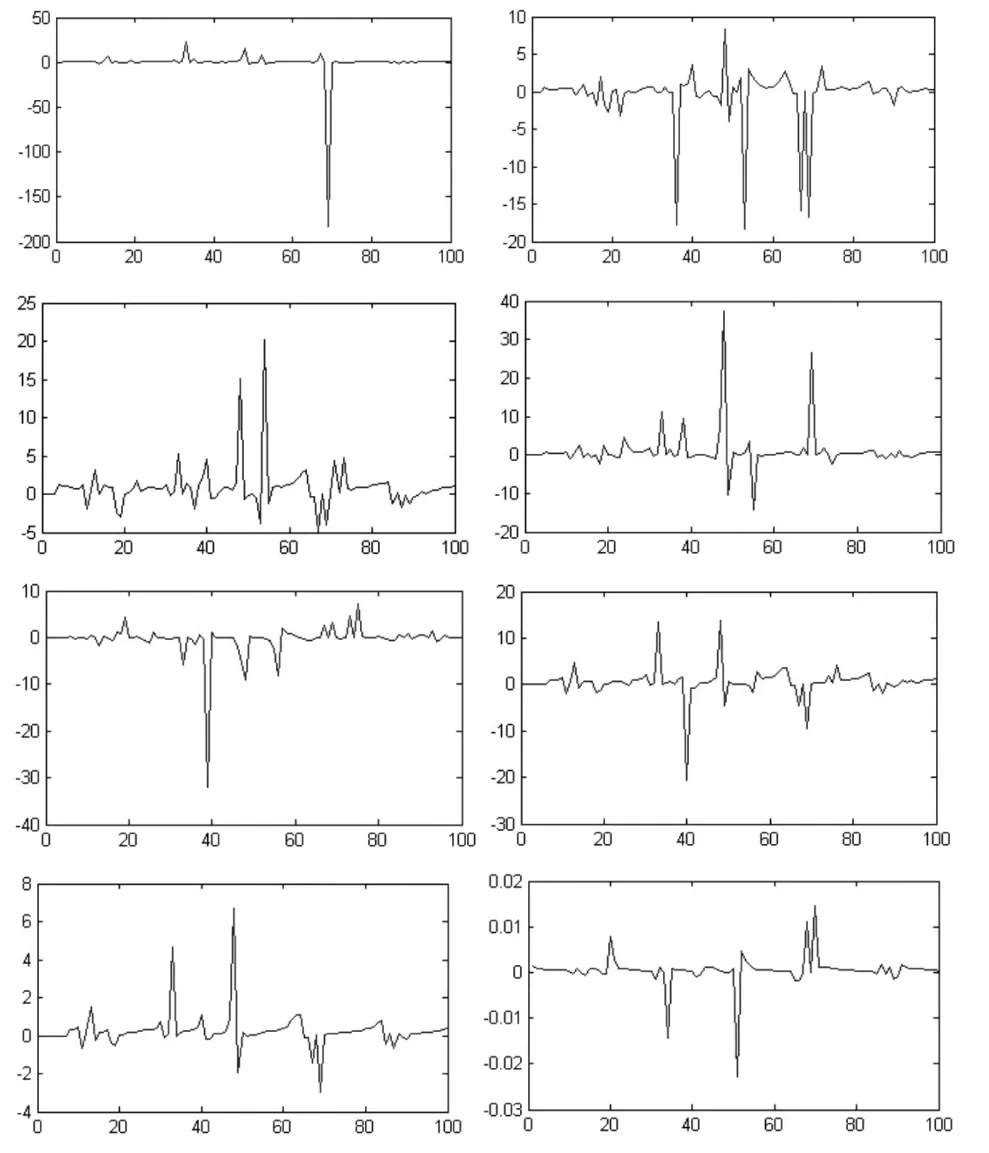
图5 用Gevers-Wouters算法进行MA参数估计
图5中分别显示的是在迭代次数t=1~100时MA的各项参数的估值(即),可以看出前期参数的估值波动很频繁,在t=80~100时参数的估值趋向于稳定。由于用于拟合模型的原数据(2010年1月至2016年3月)为75组,为了能提高预测的准确性,于是根据Gevers-Wouters算法得到的参数估值对之后每个时期分别构造模型。

根据结果调整ARMA(6,7)模型中MA过程的各个参数,由此计算出=15.461932,最后得到2016年4月国内航线旅客周转量的预测值为5032135.06。
以此类推,分别可以得到2016年5月至2017年3月的国内航线旅客周转量模型,并按照各个模型计算出预测值。通过整理汇总,与ARMA模型参数调整前的预测值相比较,如表3所示。从表3可以看出,基于Gevers-Wouters算法改进ARMA模型的参数后,误差值由原来的1.82%降到了0.74%,预测的精度明显提高。
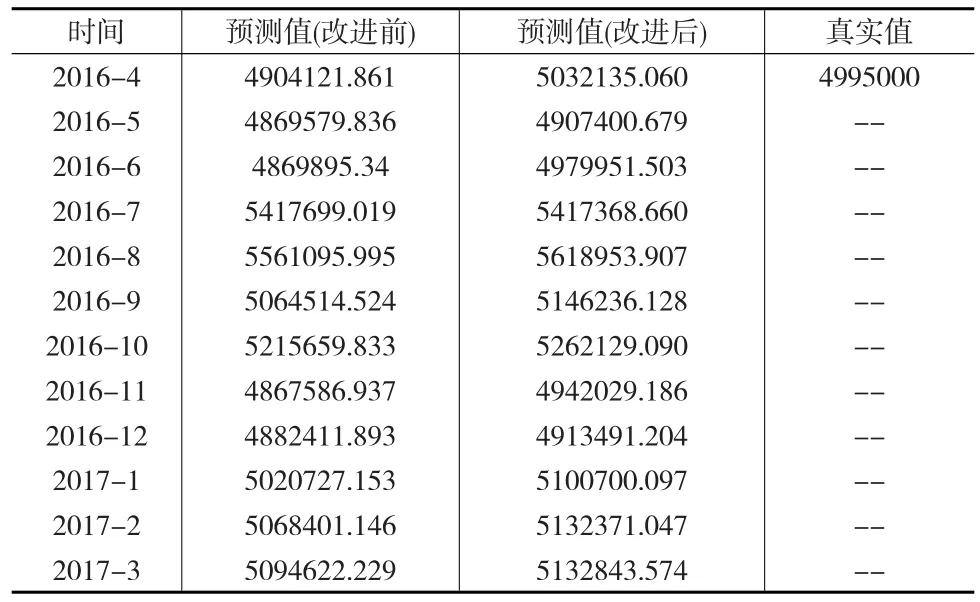
表3 模型改进前后预测值和真实值之间的比较
5 结束语
本文引入Gevers-Wouters算法,对ARMA模型中MA部分的各项参数进行调整。本文以国内航线的旅客周转量为例做实证分析,将训练集用于拟合ARMA模型,通过贝叶斯准则定阶,通过G-W算法对模型参数进行调整,最后得到的预测结果有了明显的改善。试验证明基于Gevers-Wouters算法改进ARMA模型可以有效提高预测的精度,且这种方法适用于其他的时间序列数据的预测研究,具有普遍性。
[1]吴朝阳.改进的灰色模型与ARMA模型的股指预测[J].智能系统学报,2010,5(3).
[2]邵龙锋.小波变换下ARMA改进模型预测话务总量的研究[D].重庆:重庆大学硕士论文,2015.
[3]任强,侯大道.人口预测的随机方法:基于Leslie矩阵和ARMA模型[J].人口研究,2011,35(2).
[4]何永沛.ARMA模型参数估计算法改进及在股票预测中的应用[J].重庆工学院学报,2009,23(2).
[5]黄雁勇,王沁,李裕奇.ARMA模型参数估计算法的改进[J].统计与决策,2009,(16).
[6]孙汝儒,肖迪.基于改进PSO算法对ARMA模型定阶新方法[J].计算机应用与软件,2013,30(12).
[7]Jonathan D.Cryer,Kung-Sik Chan.时间序列分析及应用:R语言[M].北京:机械工业出版社,2011.
[8]王婷.民航客运量的ARIMA模型与预测[J].五邑大学学报,2007,21(1).
[9]宋勇林.拓展的贝叶斯信息准则的一些性质[D].武汉:华中师范大学硕士论文,2014.
[10]Jafar Nouri Hajwal Hashem.时间序列模型的应用研究[D].武汉:华中师范大学硕士论文,2014.
[11]邓自立,王欣,高媛.建模与估计[M].北京:科学出版社,2007.
[12]De Keyser R M C,Van Cauwenberghe A R.A Self-Tuning Multistep Preditor Application[J].Automatic,1981,17(1).
[13]Zhang G S,Xu Y.Application of Gevers-Wouters Algorithm to Intelligent Dew Point Measurer Control Scheme[C].Switzerland:Trans Tech Publications,2014,(643).
