近非齐次指数离散灰色直接模型的适用范围及拓展
2018-03-21田念魏勇
田念,魏勇
(西华师范大学数学与信息学院,四川南充637000)
0 引言
GM(1,1)模型作为灰色系统理论核心内容之一已经广泛应用于社会、经济、科技等众多领域中[1-3]。然而在使用的过程中,学者发现GM(1,1)模型对近似齐次指数序列有较高的精度,对近似非齐次指数序列的模拟效果不佳。为了解决此问题,许多学者又把目光转向近似非齐次指数序列,对近似非齐次指数序列做了许多相应的研究,余逗[4]提出了适用于原始序列为近似非齐次指数律的GM(1,1)X新模型:刘常丽[5]为消除模型误差运用为近似非齐次指数序列GM(1,1)模型的背景值得到相应的白化微分方程:陈芳[6]运用向前差商和向后差商的加权平均值λ [x(1)(k)-x(1)(k-1)]+(1-λ)[x(1)(k+1)-x(1)(k)]作为近非齐次指数序列GM(1,1)模型的灰导数来优化模型;崔兴凯[7]运用x(0)(k)的加权均值序列px(0)(k)+(1-p)x(0)(k-1)为近非齐次指数序列GM(1,1)的灰导数来对模型进行优化和应用;崔杰等[8]根据经典灰色模型的建模机理,构建了一种基于近似非齐次指数离散函数的新灰色预测模型,利用最小二乘法和矩阵运算法推演出该新灰色模型参数的计算公式,并以微分方程为推理工具,求出了新灰色预测模型的模拟时间响应序列函数,即新灰色NGM(1,1,K)模型;王正新等[9]提出一种更为合理的背景值计算公式,从而优化了离散GM(1,1)模型,数据模拟和模型比较表明,优化后的模型模拟和预测精度有显著提高;谢乃明[10]针对非齐次指数增长规律的情况提出了NDGM(Non-Homogeneous Discrete Grey Model)离散模型,离散模型并不再与相应的白化微分方程相联系,直接从灰色方程x(1)(k+1)=β1x(1)(k)+β2k+β3角度来研究灰色预测模型;战立青[11]提出了近似非齐次指数数据的灰色建模方法,同时运用最小二乘优化了初始条件;姜爱平[12]针对现实中大量存在的非等间距近似非齐次指数序列,根据非等间距灰色模型建模机理,提出一个非等间距非齐次灰色模型,推导出模型参数的最小二乘估计及时间响应函数表达式等;童明余等[13]从近似非齐次指数序列的GM(1,1)模型时间响应函数出发,推导累加序列间的函数递推关系,并给出求解时间响应函数参数值的直接估计方法,构建一种能同时模拟近似齐次和近似非齐次指数序列的新NGM(1,1)模型;高明[14]从穆勇的研究成果背景值的一种优化表达式(1-λ)x(1)(k-1)以及形如x(0)(k)=beak+c的近似非齐次指数序列出发,发现x(0)(k)和x(1)(k)具有形如x(0)(k+1)=β1x(0)(k)+β2x(1)(k)+β3k+β4的关系式,得到一种适用于非齐次指数增长序列的直接型离散灰色模型;曾波[15]在文献[16]的思想启发下提出了DGM(1,1)直接建模法。因为传统灰色预测模型是通过对原始数列进行累加来找寻蕴含的灰指数规律,然而在原始数列为近似非齐次指数序列的前提下,若仍然对原始序列进行累加生成,反而会破坏原始数列的近似非齐次指数特征,从而导致模型失真。因此,这种不必对原始序列进行累加以及累减还原过程的建模方法,称之为DGM(1,1)直接建模法,简称DDGM(1,1)模型;谢乃明等[17]研究了近非齐次指数序列离散灰色预测模型在区间灰数序列的预测等。
以上文献都是针对近齐次指数序列和近非齐次指数序列等指数序列而言的,然而在生活中,并不是所有的序列都是近齐次指数序列或近非齐指数序列。比如线性增减序列及其与指数增减的组合序列,抛物型增减序列等都既不是近齐次,又不是近非齐次,甚至可能不单调;自然前面所讨论的各种模型模拟效果都不会很理想。为解决此问题,本文将文献[10]研究的递推关系近似为x(1)(k+1)=β1+β2k+β3x(1)(k)通过直接建模转化成研究递推关系近似为x(0)(k+1)=β1+β2k+β3x(0)(k)的建模,然后在由递推关系推导拟预测公式通项后发现适用范围除了近非齐次指数序列外,还有线性增减以及他们的组合序列,甚至还有抛物型序列,给出了近似这些特殊序列建模的参数估计方法;并证明了模型对这些特殊序列具有白化指数重合性、白化系数重合性,即(0)(k)=x(0)(k),然后通过优化初始条件,使得本文模型的模拟预测精度再次得到提高。
1 近似非齐次指数序列的灰色离散GM(1,1,β)模型
定义1[10]:设非负原始序列X(0)=(x(0)(1),x(0)(2),...,x(0)(n)),X(1)为X(0)的一次累加序列X(1)=(x(1)(1),x(1)(2),...,x(1)(n)),其中,称式(1)为近似非齐次指数序列GM(1,1,β)模型的离散形式。

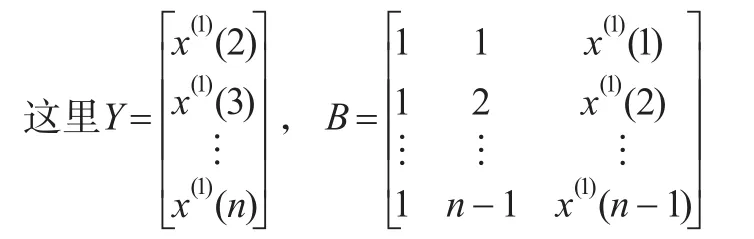
适用范围是一次累加近似满足x(1)(k+1)=β1+β2k+β3x(1)(k)的序列,由递推公式和累减还原可推得原始序列适用范围为非齐次指数形式:x(0)(k)=pβ3k+q,k=2,3,...,n,其中
2 近非齐次指数离散灰色模型直接建模
2.1 模型构造
定义2:设非负原始序列X(0)=(x(0)(1),x(0)(2),...,x(0)(n)),称式(2)为近似非齐次指数序列离散形式的GM(1,1,β)的直接建模模型。
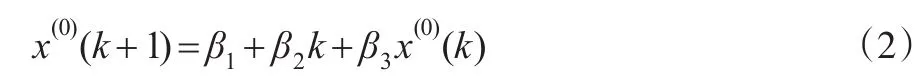

这里

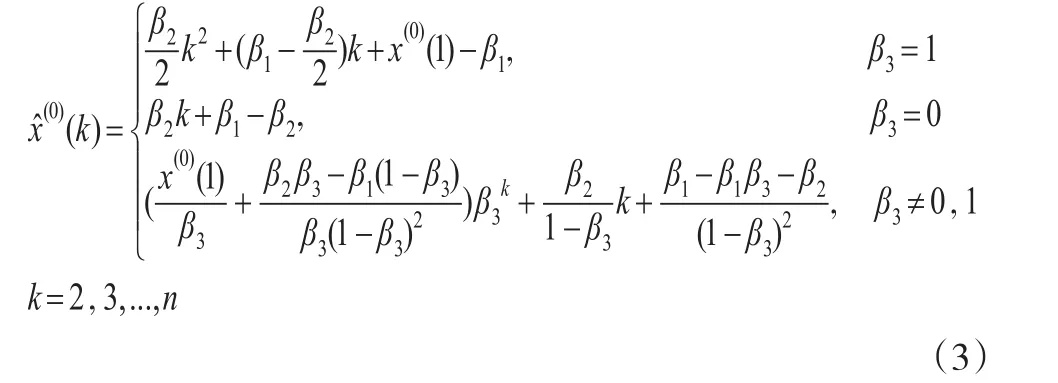
证明:分别取式(1)中k=2,3,...,n,可以得到:

把y(i)依次带入y(i+1),i=2,3,....,k,可得到:
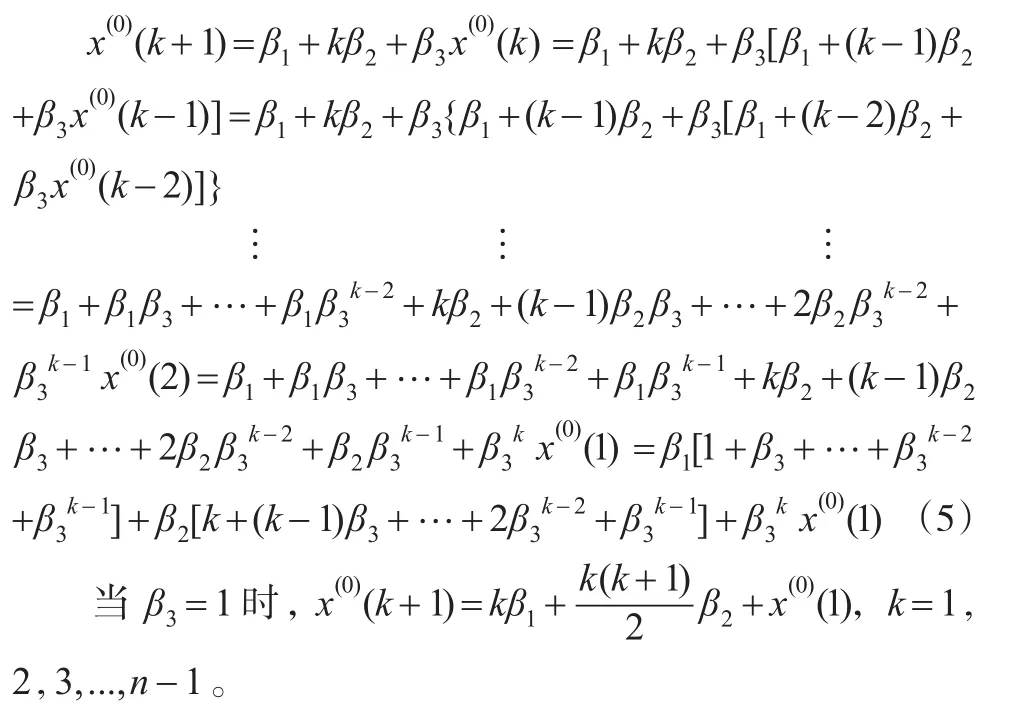
当β3=0时,x(0)(k+1)=β1+kβ2,k=1,2,3,...,n-1。
当β3≠0,1时,由等比数列求和公式得β1[1+β3+…+,又由初等数学技巧不难得到:于是k=1,2,...,n-1。则综合可知:

进一步归纳总结可知:

证毕。
2.2 模型解的两大基本类型及适用范围
通过由定理1公式(3)可将解分为两大基本类型:
(1)若β3=1,令,则x(0)(k)=Ek2+Fk+G。我们称这种形式的序列为抛物型序列。特别地,若β3=1,且β2=0,则抛物型序列退化为线性型序列。
若β3=0,令M=β2,N=β1-β2,则x(0)(k)=Mk+N。我们称这种形式的序列为线性型序列。
(2)若β3≠0,1,令

这种指数型与线性型组合序列实际上有以下三种特殊情形的组合:
当初始条件x(0)(1)=0时,有A=0,x(0)(k)=Bk+C为线性型序列。
当β2=0时,有B=0,x(0)(k)=Aβ3k+C为熟知的非齐次指数序列。
当β1=β2=0时,有B=C=0,x(0)(k)=Aβ3k为熟知的齐次指数序列。
从以上可以看出:通项同为x(0)(k)=Bk+C线性型序列,其递推关系式却有三种不同表达式,分别假定β3=1,β3=0,β3≠0,1都有与之对应的β1,β2,β3组成递推公式x(0)(k+1)=β1+β2k+β3x(0)(k)。
2.3 模型解的性质
既然模型的解只有这两种基本形式,显然只有对近似于这两类基本形式的原始序列才可能有较好的模拟效果,现在本文证明在原始序列已经是这两类基本类型的情形,模拟值将与原始值完全重合。
定理2:若原始序列为形如x(0)(k)=c1+c2k+qkc3,k=1,2,3,...,n 的指数型和线性型的组合序列,则(0)(k)=x(0)(k),即本文模型对指数和线性组合形式序列具有白化指数重合性、白化系数重合性。
证明:设原始数据序列为形如x(0)(k)=c1+c2k+qkc3,k=1,2,3,...,n ,根据定义2可得:

即对形如x(0)(k)=c1+c2k+qkc3的序列,模拟值与实际值完全相同,换句话说只有计算误差,从而对近似于这些类型的序列都有较高的模拟预测精度。
定理3:若原始序列为形如x(0)(k)=m3k2+m2k+m1,k=1,2,3,...,n 抛物型序列,则(0)(k)=x(0)(k),即本文模型对抛物型序列(m3≠0)和线性型序列(m3=0)均具有白化系数重合性。
证明:设原始数据序列为形如x(0)(k)=m3k2+m2k+m1,k=1,2,3,...,n 的抛物序列,根据定义2可知:
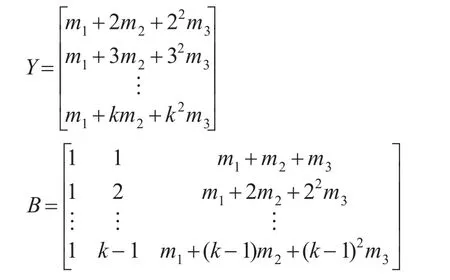
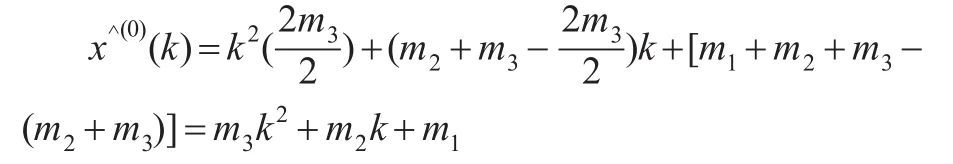
即本文模型对形如x(0)(k)=m3k2+m2k+m1的抛物型序列而言,模拟值与实际值完全相同,换句话说只有计算误差,没有模型误差。
除了严格满足这三种基本类型的序列没有误差外,近似满足这两种基本类型的序列也应有较高的模拟预测精度,这就是本模型的适用范围。
2.4 模型初始条件的优化
模型建模通常是选取实际初始值作为灰色模型的初始条件,也即指数曲线通过第一个点,但总体规律不一定过这个点。当实际初始值偏离整体规律时,这样建立的模型也会偏离整体规律,得到的模型会有较大的误差。所以为了减少误差,本文运用模拟值和原始值的误差平方和最小确定最优初始条件。设初始条件为(0)(1)=c,选取c使得原始序列与其模拟值的误差平方和最小。即可得:

3 模型建模精度比较
3.1 理论数据建模比较
例1:为了模拟指数增减和线性增减序列组合灰色预测模型,本文引用文献[15]中的4组不同形状的数据建模,而本文在此基础上构建5组新的数据X5-X9序列。其中X1={1.2,2.9,4.2,5.1,5.8}为上升指数序列,X2={5.8,5.1,4.2,2.9,1.2}为下降指数序列,X3={5,11,29,83,245}为严格非齐次指数函数序列,X4={1.4,2.0,2.8,3.9,5.4}为近似非齐次指数函数序列,X5={5,16,45,128,373}为严格的指数和线性的组合序列,X6={1.4,3.4,6.2,10.1,15.5}为近似指数增长和线性增长序列,X7={-15.2817,-30.6109,-37.9145,-23.4018,50.4132}为严格指数增和线性减组合波动序列,X8={13.2817,23.6109,25.9145,6.4018,-72.4132}为严格指数减和线性增的组合波动序列波动序列,X9={4,11,22,37,56}为严格抛物序列。并将本文提出的模型与文献[15]提出的两种直接建模模型进行比较,其中模型1为文献[15]中的DGM(1,1)模型,模型2为文献[16]中的DDGM(1,1)模型,本文模型没有优化初始值的模型为模型3;本文优化了初始值的模型为模型4。通过表1进行相应的比较,分析模拟结果并比较模拟精度。
根据文献[15]知,模型1的最终表现形式是离散齐次指数函数,模型2的表现形式是近非齐次指数函数,故根据模型的这一特征可知模型1适用于齐次指数序列,模型2适用于齐次或非齐次指数序列,而本文的模型既适用于齐次或非齐次指数序列又适用于波动序列、抛物序列等。由于X1和X2都是近齐次指数序列,故模型1和模型2与本文两种模型对X1和X2都有很好的效果,模拟精度(此处规定为:1-平均相对误差)相差不大;X3序列是高增长但为严格非齐次指数序列,而模型2和本文模型对这类序列都有指数重合性,故都没有误差;且根据序列X1-X9的模拟数据可以看出,本文的模型3和模型4的模拟精度均高于文献[15]的模型1和模型2,说明本文模型无论是对指数增减和线性增减的组合序列,还是对抛物增减序列,无论是单调递增、单调递减序列,还是波动序列,都有较好的效果。本文不仅在原有模型基础上大幅度提高了模拟预测精度,而且相对于近期优化模型也是再次提高。(其实文献分成凸凹形状的所有数据本文都逐一验证过有类似结果,因篇幅所限不一一列出)由此可知本文不只局限于单调的序列,也不只是针对指数和近指数序列,故本文在以前文献的基础上扩大了模型的适应范围,如抛物、线性,以及他们与非齐此指数序列所有可能的加减组合都是本文新增适应范围。同时针对严格严格非齐次、严格指数增长和线性增长组合序列、严格指数增和线性减组合波动序列、严格抛物序列等严格序列能够完全模拟,换句话说,对于前面讨论的严格序列只有计算误差,没有模型误差。
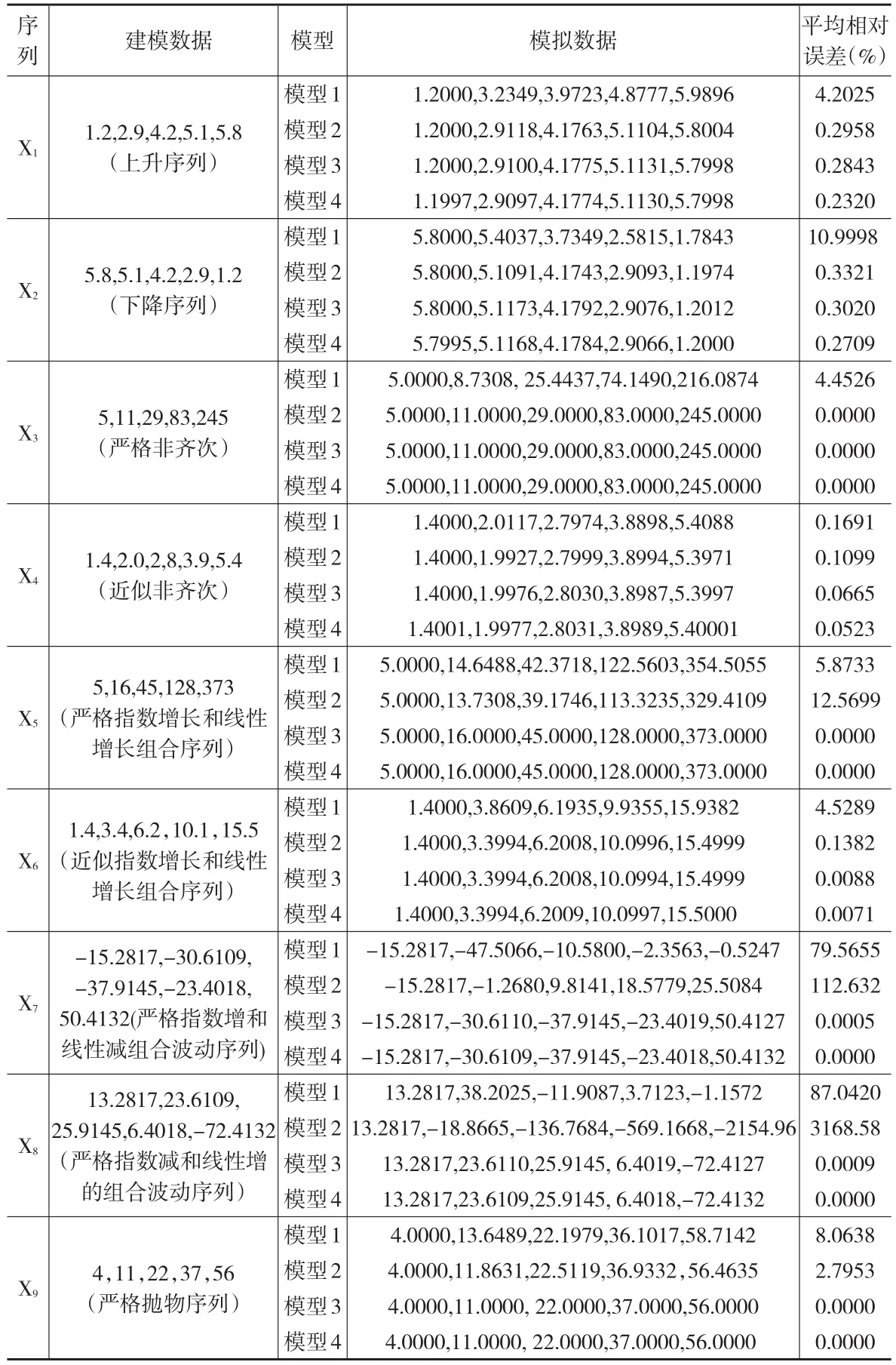
表1 模拟值及模拟精度
3.2 应用实例比较
例2:本文以文献[14]中2003—2008年西安市第三产业生产总值(数据来源于《西安统计年鉴2009》中综合类)为原始数据,X=[488.56,565.26,664.52,764.03,908.71,1098.89],文献[10]模型称为模型1,文献[14]模型称为模型2,本文模型没有优化初始值的模型为模型3。本文优化了初始值的模型为模型4,建模结果及数据分析见表2。

表2 三种不同的模型的误差比较
文献[14]中模型1和模型2都比原始模型更优(由于篇幅所限,没有列出原始模型),而从表2中的结果可以看到,本文的建模结果,不论是平均相对误差还是绝对误差平方和都明显优于文献[14]。由此可知本文近非齐次指数离散灰色模型直接建模不仅提高了拟合精度,还扩大了模型适用范围。
4 结束语
本文通过离散化思想和直接建模思想,对原始序列直接建模得到非齐次指数离散灰色预测新模型。以指数增减序列和线性增减序列的组合序列、抛物线增减序列建模突破传统齐次、非齐次序列建模的范围。其中离散化思想使模型不再与相应的白化微分方程相联系,直接从离散的角度来研究灰色模型;直接建模思想则不必对原始序列进行累加建模以及累减还原,直接得到原始序列的模拟值和预测值,使计算更加简单,从而减少了相应的误差。本文同时将适用范围拓展到近似非齐次指数增减序列与线性增减序列的组合序列、抛物线增减序列等情形,推导了待定系数的求解公式,从理论上证明了新模型对严格非齐次指数增减序列与线性增减序列的组合序列、抛物线增减序列具有白化指数、系数重合性;利用误差平方和最小对新模型的初始条件进行优化,使得本文模型的模拟预测精度再次得到提高;最后通过实例验证了所述结论,说明了本文方法的有效性和可行性,具有一定的理论价值和应用价值。
[1]邓聚龙.灰预测与决策[M].武汉:华中科技大学出版社,2002.
[2]刘思峰,党耀国,方志耕.灰色系统理论及其应用[M].北京:科学出版社,2004.
[3]Liu S F,Forrest J.The Role and Position of Grey System Theory in Science Development[J].The Journal of Grey System(UK),1997,9(4).
[4]余逗,魏勇.非齐次指数序列的GM模型[A].第16届全国灰色系统学术会议论文集[C].北京:中国高等科学技术中心,2008.
[5]刘常丽,屈绍建.一类GM(1,1)模型白化方程的优化[J].数学的实践与认识,2015,45(4).
[6]陈芳,魏勇.近非齐次指数序列GM(1,1)模型灰导数的优化[J].系统工程理论与实践,2013,33(11).
[7]崔兴凯,路秀英.基于NGM(1,1,k)模型的农产品产量预测方法[J].微电子学与计算机,2011,28(8).
[8]崔杰,党耀国,刘思峰.一种新的灰色预测模型及其建模机理[J].控制与决策,2009,24(11).
[9]王正新,党耀国,刘思峰.基于离散指数函数优化的GM(1,1)模型[J].系统工程理论与实践,2008,(2).
[10]谢乃明,刘思峰.离散灰色模型的拓展及其最优化求解[J].系统工程理论与实践,2006,28(11).
[11]战立青,施化吉.近似非齐次指数数据的灰色建模方法与模型[J].系统工程理论与实践,2013,33(3).
[12]姜爱平,张启敏.非等间距近似非齐次指数序列的灰色建模方法及其优化[J].系统工程理论与实践,2014,32(12).
[13]童明余,周孝华,曾波.基于直接估计法的NGM(1,1)模型拓展[J].控制与决策,2015,30(10).
[14]高明.一种适用于非齐次指数增长序列的接型离散灰色模型[J].统计与信息论坛,2010,25(4).
[15]曾波,刘思峰.近似非齐次指数序列的DGM(1,1)模型直接建模法[J].系统工程理论与实践,2011,2(31).
[16]王义闹.GM(1,1)逐步优化直接建模方法的推广[J].系统工程理论与实践,2003,23(2).
[17]Xie N M,Liu S F.Interval Grey Number Sequence Prediction by Using Non-homogenous Exponential Discrete Grey Forecasting Model[J].Journal of Systems Engineering and Electronics,2015,26(1).
