基于信息值的相关属性约减—加权二分类朴素贝叶斯算法研究
2018-03-21杨立洪李琼阳李兴耀
杨立洪,李琼阳,李兴耀
(华南理工大学数学学院,广州510640)
0 引言
朴素贝叶斯分类(Naive Bayes Classification)算法是目前公认的一种简单有效的分类算法,它是一种基于概率的分类方法,被广泛地应用于模式识别、自然语言处理、机器人导航、机器学习等领域。朴素贝叶斯算法是基于特征项间独立、对目标变量影响力一致的假设,但实际应用中极少数问题能满足此假设。为此许多学者致力于改进朴素贝叶斯算法,以期提高算法的普适性和准确率。改进之处主要体现在两个方面:一是在属性选择上预把控;二是衡量各属性对目标变量的影响程度,对属性加权。
在属性选择上,Geenen P Ld等[1]提出一种基于互信息选择特征属性的方法,并利用朴素贝叶斯算法在二分类问题上取得了极好的分类效果。魏浩和丁要军[2]提出用属性关联度表示一个属性和类属性间的相关性,反映这个属性对分类结果影响的程度;用属性冗余度表示一个属性和其他属性之间相关性,反映这个属性和其他属性间的依赖度。王行甫和杜婷[3]提出利用CFS算法选择特征属性。焦鹏等[4]提出将属性先验分布的参数设置加入到属性选择的过程中,并研究当先验分布服从Dirichlet分布及广义Dirichlet分布情况下的具体实践方案。研究出一种加权朴素贝叶斯算法,通过对不同的特征项提供不同的权值,削弱特征项之间的相关性。
在属性加权上,饶丽丽等[5]提出在传统权重计算基础上,考虑到特征项在类内和类间的分布情况,另外还结合特征项间的相关度,调整权重计算值,加大最能代表所属类的特征项的权重。Jiang L等[6]提出在训练集中深度计算特征加权频率,估计朴素贝叶斯的条件概率。Lungan Zhang等[7]提出了两种自适应特征加权方法:一是基于树的自适应特征加权;二是基于信息增益率的特征加权。
为了解决朴素贝叶斯算法的两个固有缺陷,本文将构建基于信息值的相关属性约减—加权二分类朴素贝叶斯模型,有效解决属性相关、属性加权的问题。在判定样本类别归属时,采用自适应学习选择合适的阈值,以此削弱不平衡样本集的影响,提高模型的准确率。最后在某运营商提供的垃圾短信用户行为消费特征样本数据上进行实证分析,结果表明:基于信息值的相关属性约减—加权二分类朴素贝叶斯较传统朴素贝叶斯模在模型准确率上有显著提升。
1 朴素贝叶斯算法
朴素贝叶斯算法的分类原理是通过某对象的先验概率,利用贝叶斯公式计算出其后验概率,具有最大后验概率的类则为该对象所属的类。朴素贝叶斯是在贝叶斯分类法的基础上提出的,该算法满足一个简单的假定,即在给定目标值时属性值之间相互条件独立。
朴素贝叶斯分类算法的工作过程如下:
(1)设A表示训练样本的属性集,有m个属性A1,A2,…,Am;C表示类集合,有k个类C1,C2,…,Ck;每个数据样本X用一个m维特征向量来描述m个属性的值,即:X=(x1,x2,…,xm),其中xi∈Ai(1≤i≤m)。
(2)对训练样本集进行统计,计算得到每个特征属性在各类别的条件概率估计,即:

(3)对每个类别计算后验概率,根据贝叶斯定理及朴素贝叶斯算法的假定可知:
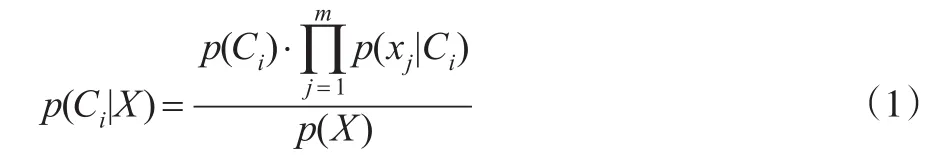
(4)取最大后验概率项作为样本所属类别:

2 基于信息值的相关属性约减—加权二分类朴素贝叶斯算法
2.1 信息值
信息值简称IV,衡量自变量对目标变量的影响程度,是建模时筛选变量的一个非常重要的指标。它起源于香农提出的信息理论,与广泛应用的熵有极大的相似性,主要适用于二分类模型。在介绍信息值之前,有必要先引入WOE(weight of evidence)。为方便表述,将二分类目标变量标识为0、1,其中1表示违约,0表示正常。WOE实质上是表示自变量取某个值时对违约比例的影响,例如当自变量取值为i时对目标变量违约比例的影响woei的计算公式如下:

其中,Bi指当该自变量取值为i时的违约样本数,Gi指该自变量取值为i时的正常样本数。BT指建模样本数据中总的违约样本数,GT指建模样本数据中总的正常样本数。
信息值衡量一个变量的信息量,例如对于一个有n个取值的自变量而言,该自变量的信息值计算公式如下:
当层间位移角到达2%rad,即梁加载中心点位移25.46 mm时,在梁端位移负向最大位移时,发生一声巨响,这是用简易扳手可拧动梁下翼缘与角钢相连的左排螺栓,但肉眼看不出。当层间位移角到达3%rad(38.19 mm)时,响声不间断的会发出,角钢略微掀起。

从计算公式上可以看出,信息值是自变量WOE值的一个加权组合,其值的大小决定了自变量对目标变量的影响程度。从形式上看来,信息值与信息熵也是极为相似的。
通常认为,0.1≤IV≤0.3时认为该变量对目标变量有中等影响力;0.3≤IV≤0.5时认为该变量对目标变量有较强影响力;IV≥0.5时认为该变量对目标变量有极强的影响力。
2.2 属性约减
朴素贝叶斯算法要求建模的自变量之间相互独立,但在实际应用过程中,参与建模的变量之间往往会存在一定程度的相关性。相关系数是反映两个变量之间相关程度的一个重要度量,计算公式如下:
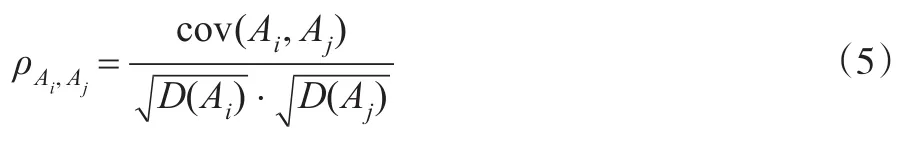
一般情况下,0.4≤ρAi,Aj≤0.6,认为Ai与Aj之间中等程度相关;0.6≤ρAi,Aj≤0.8,认为Ai与Aj之间强相关;0.8≤ρAi,Aj≤1,认为Ai与Aj之间极强相关。
为了尽可能满足朴素贝叶斯算法的假设条件,有必要对变量进行属性约减。约减规则如下:
(1)根据IV值筛选一批对目标变量影响程度较大的自变量,一般选择IV值大于0.3的变量。
(2)计算(1)中筛选出的自变量之间的相关系数,一般当ρAi,Aj>0.5时,即可认为Ai与Aj之间有较强的相关性,不宜全部进入模型。
(3)若ρAi,Aj>0.5,且变量Ai的IV值大于变量Aj的IV值,则只选择变量Ai参与建模。
2.3 属性加权
朴素贝叶斯算法选择后验概率最大的类别作为归属,在计算中默认各属性对目标变量的影响程度一致,但由于信息值已知,各自变量对目标变量的影响程度是有差异的,因此考虑利用各属性的IV值进行属性加权。经由前文中基于信息值和相关属性约减筛选出对目标变量有强影响力的m个变量,并保证了各变量之间几乎独立。假设这m个变量蕴含了所有的信息,则属性j所占的比重ej即为:

信息值的比重越大,该变量对目标比变量的影响力就越大,由于条件概率p(xj|Ci)的取值范围是(0,1),为此可以按照如下公式修正权重,即:
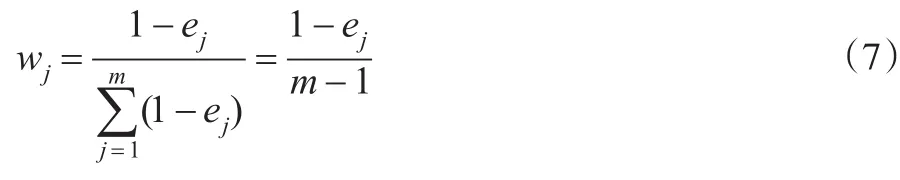
对后验概率公式进行修正:
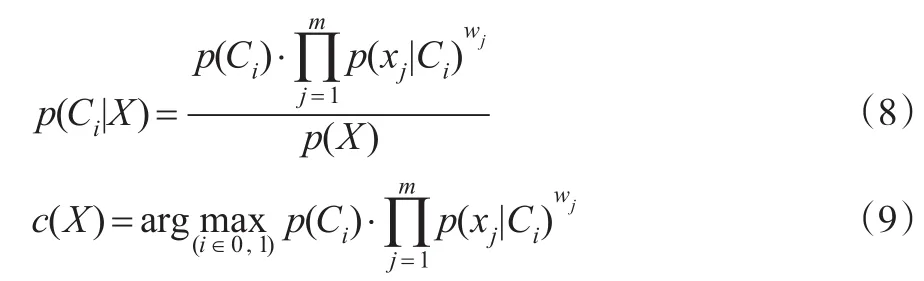
选择后验概率最大的类别作为归属。
2.4 自适应学习选择合适的阈值
在二分类朴素贝叶斯算法中,若p(C1|X)>p(C0|X),则把样本X归为C1类。但有时样本集中在二类样本的数量上相差极大,样本分布极不均衡,若仍按上述方式判定类别归属,则极有可能误判。考虑当p(C1|X)>l⋅p(C0|X)时,把样本X归为C1类,l值的具体选择可以依赖其在训练数据集上的表现。一般情况下,若C1类的样本错判到C0类的较多,可以考虑在(0,1)内选择合适k值;若C0类的样本错判到C1类的较多,可以考虑在(1,50)内选择合适k值,以此来提高模型的准确率。
3 实证
3.1 数据的收集和处理
某运营商提供了用户行为消费特征样本数据共78258条,其中垃圾短信用户样本数据11837条,用1标识;正常用户66421条,用0标识。数据集有当月消费额、品牌、通话时长、发送短信条数、短信回复率、账户余额、是否为垃圾短信用户等共56个属性。下面将利用基于信息值的相关属性约减—加权朴素贝叶斯算法来进行建模。
3.2 基于信息值进行属性约减—加权
在垃圾短信用户识别过程中,是否是垃圾短信用户是目标变量。利用信息值的计算公式,计算除目标变量的其他55个变量的信息值。按照上文中的属性约减规则进行属性约减,最终选定7个变量参与建模,变量的信息值、权重、相关系数如表1和表2所示。

表1 建模变量的信息值、权重

表2 相关系数矩阵
由参与建模的7个变量的相关系数矩阵可以看出,变量之间基本满足条件独立的假设。
3.3 模型构建及对比检验
在数据集中按照7:3的比例进行分层随机抽样,划分训练样本与检验样本。在利用模型求出每一个样本的后验概率之后采用自适应学习选择合适的l值,判别每一个样本的归属。经实验发现,当l=0.25时模型的准确率最高。至此,当p(C1|X)>0.25⋅p(C0|X)时,判断样本X为垃圾短信用户。
分别利用改进的朴素贝叶斯算法和传统朴素贝叶斯算法建立模型,二者在训练集和测试集的建模结果如表3所示:

表3 模型改进前后效果对比
由表3可以看出基于信息值的相关属性约减—加权朴素贝叶斯算法较传统的朴素贝叶斯算法在建模效果的准确率上有显著提升。
4 结论
朴素贝叶斯算法是目前比较高效经济的分类算法之一,也是常用的十大算法之一。本文在朴素贝叶斯算法的基础上,针对朴素贝叶斯算法的固有缺陷,提出基于信息值的属性约减—加权改进方法,该方法能有效处理相关属性,使之尽可能满足朴素贝叶斯的理论假设。同时利用属性的信息值为属性赋予的权重,采用自学习选择合适的判定阈值,以降低不平衡样本对模型的影响,从而最大程度上提高模型的准确率。
在垃圾短信客户识别的实际应用过程中也发现,基于信息值的属性约减—加权改进朴素贝叶斯算法较传统的朴素贝叶斯算法在准确率上有显著提升。
[1]Geenen P L,Gaag L C V D,Loeffen W L A,et al.Constructing Naive Bayesian Classifiers for Veterinary Medicine:A Case Study in the Clinical Diagnosis of Classical Swine Fever[J].Research in Veterinary Science,2011,91(1).
[2]魏浩,丁要军.一种基于相关的属性选择改进算法[J].计算机应用与软件,2014,31(8).
[3]王行甫,杜婷.基于属性选择的改进加权朴素贝叶斯分类算法[J].计算机系统应用,2015,24(8).
[4]焦鹏,王新政,谢鹏远.基于属性选择法的朴素贝叶斯分类器性能改进[J].电讯技术,2013,(3).
[5]饶丽丽,刘雄辉,张东站.基于特征相关的改进加权朴素贝叶斯分类算法[J].厦门大学学报:自然科学版,2012,51(4).
[6]Jiang L,Li C,Wang S,et al.Deep Feature Weighting for Naive Bayes and Its Application to Text Classification[J].Engineering Applications of Artificial Intelligence,2016,(52).
[7]Wang S,Jiang L,Li C.A CFS-Based Feature Weighting Approach to Naive Bayes Text Classifiers[J].Knowledge-Based Systems,2016,(100).
