基于广义熵的地区工业污染排放差异测度与分解
2018-03-21陆宇嘉
陆宇嘉
(西南科技大学a.经济管理学院;b.四川循环经济研究中心,四川 绵阳 621010)
0 引言
近年来,气候变化已成为全球性问题。作为经济总量最大的发展中国家,中国的经济增长伴随着庞大的资源环境消耗,工业污染排放量逐年上升,尤其是最近几年,频发的雾霾天气,引发了社会各界的广泛关注。在此背景下,中国政府积极在各地推行节能减排政策。由于各省资源禀赋以及在产业结构调整上的不一致,中国的环境污染本身就存在着较大的地区差异。而随着相关产业政策的实施,污染产业逐渐向中西部地区转移,使得地区间的环境不平等问题更加明显。全国污染减排目标的实现不仅有赖于技术、法规和市场化机制等多方面的保障,而且需要各地区的协同努力。因此,准确测度并把握地区环境不平等的现状和变化趋势,就成为合理分配减排治污任务、调整相关产业和能源政策的重要前提。
在过去二十多年间,一些学者采用收入不平等度量分析工具分析跨国或单个国家区域间的CO2排放差异[1-3],另一些学者则针对中国地区碳排放差异进行了研究[4-8]。还有学者对工业污染物的排放差异进行了研究[9]。虽然研究CO2排放差异的文献较多且较全面,然而需要指出的是,工业污染排放仍然是现阶段中国环境污染的主要来源,但相关研究尚不多见,目前涉及的文献还只是以单个省为研究对象,没有从国家层面上来考虑工业污染排放强度的差异,这就意味着难以从宏观整体上对各省市或各地域工业污染排放的减少进行谋篇布局,缺乏系统性的综合考量。那么,对于不同类型的工业污染物,各地区间的排放差异是否呈现相似的变化趋势?三类工业污染物的地区排放差异程度相同吗,是否有规律可循?怎样的系统原因引起了国内地区间的环境不平等?为解答以上问题,本文将通过省际和东、中、西部三大区域的双重视角,利用广义熵指数(Generalized Enropy,GE)中的平均对数离差T0和泰尔指数T1对1997—2014年工业废水、废气以及固体废弃物三类工业污染物排放强度差异进行测度,并在此基础上对测度结果进行相应分解,以期深入而全面地考察这一问题。
1 检验方法及数据说明
1.1 广义熵指数(GE)及其分解方法
作为在收入不平等度量中被广泛运用的指标工具,广义熵指数(Generalized Entropy)的数学形式如下:

在式(1)中,xi表示个体收入,是收入均值,n是样本容量,i∈(1,2,...,n),。β为参数,常取值0和1。β取较小数值时,广义熵指数能更敏锐地观测到低收入群体的收入变化。
当β等于0时,此时为平均对数离差T0,也常被称为泰尔L指数或第二泰尔指数:

当β等于1时,为泰尔指数T1,也被称为泰尔T指数或第一泰尔指数:

根据式(2)和式(3)可以推导出测度地区工业污染排放(Pollution,用P表示)差异程度的广义熵指数,则地区工业污染排放差异的T0指数如下:

在式(4)中,i为地区,某一区域的工业生产总值用Ii表示,I为全国层面的工业生产总值。Pi表示地区i的工业污染排放量,P为全国层面的工业污染排放总量。需要指出的是,工业污染物排放来自于工业生产,因此采用单位工业产值的污染物排放量(即排放强度)而非人均排放量来测度地区工业污染排放状况更合适。
同样,根据前文的变量转换可以得到工业污染排放差异的T1指数:

进一步地,根据测得的地区工业污染排放的广义熵指数,可以利用Shorrocks和Wan[10]提出的方法做出如下分解:

根据式(6),总体差异程度可以被分解为区域内部差异和区域间差异。若以泰尔L指数T0为例,则有:
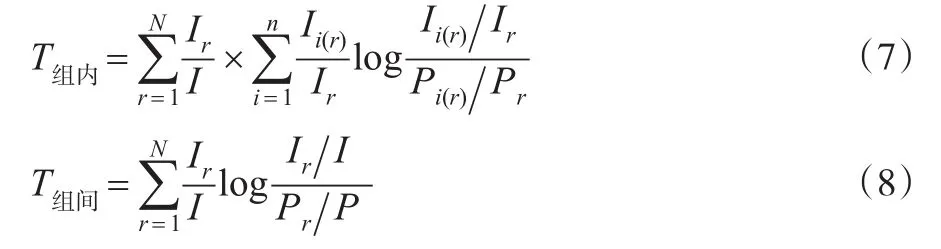
在式(7)和式(8)中,各变量含义与前文类似,只是r特指东中西部中某一地区,i为地区r中的某一省份。N为地区的总个数。相同地,泰尔T指数T1也可做类似分解,这里就不再一一赘述。
进一步在等式(6)左右两边同时除以T总体,可更深入地掌握区域间差异和区域内部差异分别对总体差异形成的影响程度,即有区域内贡献率为T组内T总体,区域间贡献率为T组间T总体。此外,若考虑各子区域对总体差异贡献的大小,需先计算出各子区域的平均对数离差T0,这里定义为Tr,则子区域对总体差异贡献率可表示为(Ir/I)×(Tr/T总体)。
1.2 数据说明
鉴于数据的可得性和时间的连续性,本文的观测对象包含了全国30个省、市、自治区(西藏以及港、澳、台地区除外)。各省份单位工业产值的工业污染排放量数据是由各省份各类工业污染物排放总量(包括工业废水排放量、工业SO2和工业烟尘排放量加总构成的工业废气排放量以及工业固体废物产生总量)除以各省份工业总产值得到。其中,各省份工业产值数据按照1997年价格进行调整,所有的数据均来自于1998—2015年《中国统计年鉴》以及相应年份的《中国环境统计年鉴》①由于2016年《中国环境统计年鉴》中工业废气排放口径发生了变化,不再对工业烟尘排放量进行统计,为了保持统计口径的一致性从而得到更准确的实证结果,数据只采用1998—2015年的相关统计年鉴。。
2 地区工业污染排放差异度量结果分析
2.1 分省排放差异度量
根据式(4)和式(5),将1997—2014年中国省份间的工业污染排放广义熵指数T0和T1的计算结果进行描点,可以得到图1至图3。为便于比较,在图中加入了工业污染排放差异的GINI计算结果,GINI、T0、T1的数值代表工业污染排放强度的不平等程度,18年的观测时期能够动态且全面地显示排放差异的变动趋势。
如图1所示,对于观测期的每一个年份,各省份工业废水排放强度的基尼系数波动程度大体上低于平均对数离差T0和泰尔T1的波动程度。以1999年为例进行说明,这一年省际间工业废水排放强度差异的T0和T1分别增加了35.71%和41.90%,而基尼系数只增加了14.42%;再以2006年为例,前两个指数分别减少了11.92%和15.01%,基尼系数却只降低了7.09%。由于T0能更敏锐地观测到排放强度较低的省份波动,相反T1能较敏锐地观测到排放强度较高的省市波动。因此总体而言,相较于工业废水排放强度水平居中的省份,高排放强度和低排放强度的省份的相对排位发生了较大变动。波动趋势显示,从1997—2014年,三种指数测度下的全国工业废水排放强度的差异变动大体相同,表现出倒U型的变动趋势。这说明随时间变化,全国省份间工业废水排放强度的差异程度先升高后降低。需要特别指出的是,在2005年,三种不平等指标的测度结果均最大,分别为0.267、0.124和0.133,表明此时的不平等程度最高。此后,全国工业废水的排放强度差异基本呈现出波动性下降趋势,2014年工业废水排放不平等程度达到最低点。

图1 1997—2014年全国工业废水排放强度的差异变动
如图2所示,全国工业废气排放强度差异也经历了先增加后减小的倒U型变动状态。以2004年为截点,可以将工业废气排放强度不平等分为1997—2004年和2004—2014年两个变化阶段。在前一阶段,无论是哪种指标,各省份工业废气排放强度都处于上升趋势。其中2000年的升幅最高,GINI、T0、T1分别增长 10.03%、18.80%、18.89%。在后一阶段,全国各省份工业废气排放强度差异基本上逐渐降低。在2008年,基尼系数、T0、T1的下降幅度最大,分别降低了6.5%、13.54%、13.70%。基尼系数的波动程度在样本期内最低,说明相对于工业废气排放强度较高和较低的省份,水平居中省份产生的变化最小。此外,和工业废水排放相比,全国各省份工业废气排放的差异性更加突出,GINI最低值为0.335,远高于工业废水的GINI最高值0.267。
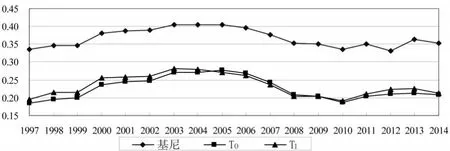
图2 1997—2014年全国工业废气排放强度的差异变动
图3显示了1997—2014年全国工业固体废弃物排放强度差异的动态变化趋势。从图形上看,和前文两种工业污染排放物不同,工业固体废弃物的不平等波动趋势类似于N型。此外,三种不平等指标的度量结果都表明工业固体废弃物的排放差异程度较高,不仅GINI的平均数值高达0.441,T0和T1均值也分别达到0.343和0.321,并且在2014年达到最大值0.482。而且与图1和图2进行横向对比发现,全国工业固体废弃物的排放差异也远大于工业废水和工业废气。

图3 1997—2014年全国工业固体废弃物排放强度的差异变动
2.2 三大区域工业污染排放差异度量
2.2.1 区域工业污染排放强度的差异
由于受到资源禀赋、历史以及地理因素的影响,中国的地区发展极不平衡。而各省工业污染排放差异度量仅能反映总体上的环境负担不平等,不能够体现出区域层面上的环境负担差异。因此本文将从东、中、西部视角,测度区域内部和区域间的工业污染排放差异,并具体分析不同层次差异的形成对全国总体工业污染排放不平等的影响程度。将总体差异拆分为组间和组内差异的理想指标为广义熵指数,而T0更偏好公平,在检测差异程度时表现得更为敏锐,后文将用它来度量和分解东、中、西部区域工业污染排放强度差异。表1至表3显示了1997—2014年三大区域的三类工业污染物排放强度差异及相应的总体差异分解结果。
表1显示,从1997—2014年,东、中、西部工业废水排放不平等分别为0.106、0.069和0.068,这表明东部地区内各省份工业废水排放强度不平等的程度最高,中部次之,西部最低。结合资源利用效率进行分析,在整个样本期内,西部平均贡献了全国总体工业产值的12%,排出的工业废水占全国总量的26%;中部平均贡献了全国总体工业产值的26%,排出的工业废水占比为28%;而东部对全国工业产值的平均贡献率最大,达到62%,而排出的工业废水占比为53%,说明即使东部地区的工业排放不平等程度最高,其资源利用效率却在三个地区中最好。通过总体差异的两种差异层次分解可以发现,区域间和区域内差异在2014年都出现了冲高式大幅度增长,在样本期内区域间差异一直小于区域内差异,且区域间差异显示出波动性下降状态,区域内差异则先增大后减小。
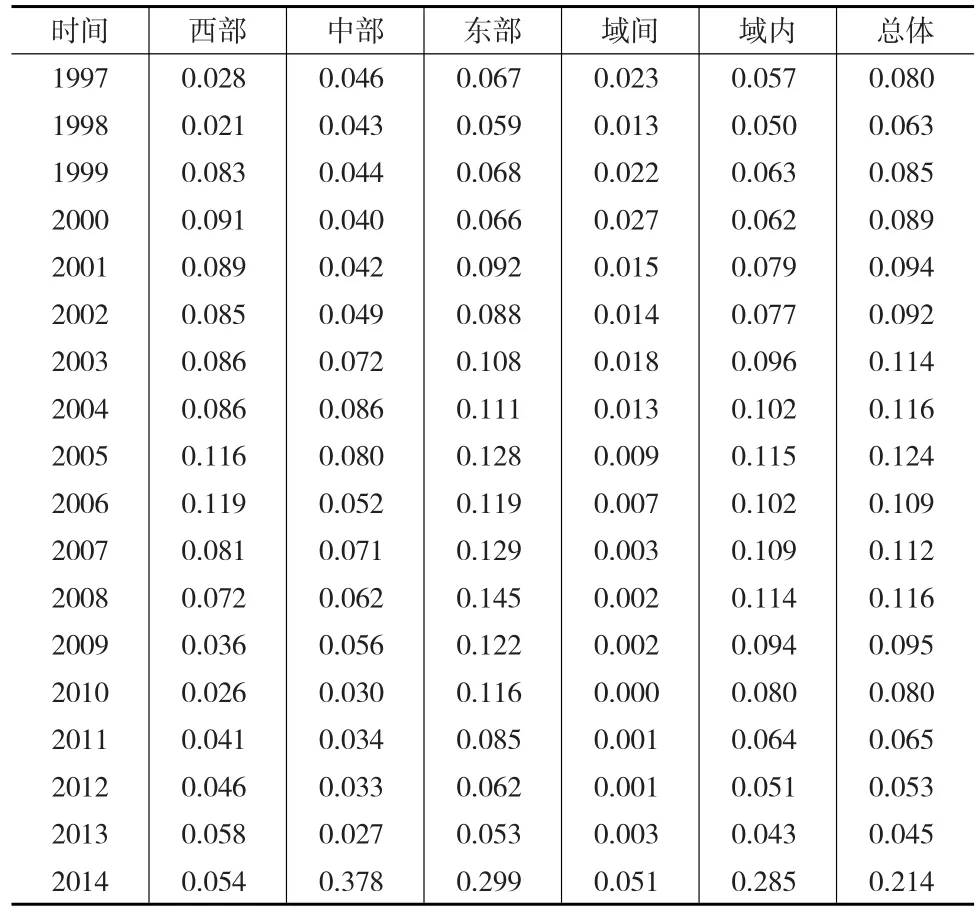
表1 三大区域工业废水排放强度差异
具体观察波动性特征可知,东部区域内工业废水排放不平等从1997年开始持续扩大,到2006年不平等程度达到最高。与此同时,中部区域内差异呈现先升高后降低的倒U型波动,西部的不平等程度在提升的过程中逐渐缩小与东部的差距。东、中、西部各自的区域内差异均值在这一时期分别为0.090、0.055和0.080。在2006年之后的时期内,东部的工业废水排放差异始终维持在三个区域中最高的水平上,均值为0.162。中部和西部差距随时间逐渐减小,但在2014年又表现出趋势背离,均值分别为0.0086和0.052。总体而言,东、中、西部区域内各省份工业废水排放差异都经历了先上升后下降的过程,但东、中、部省份工业废水排放在2014年的变动却较明显。
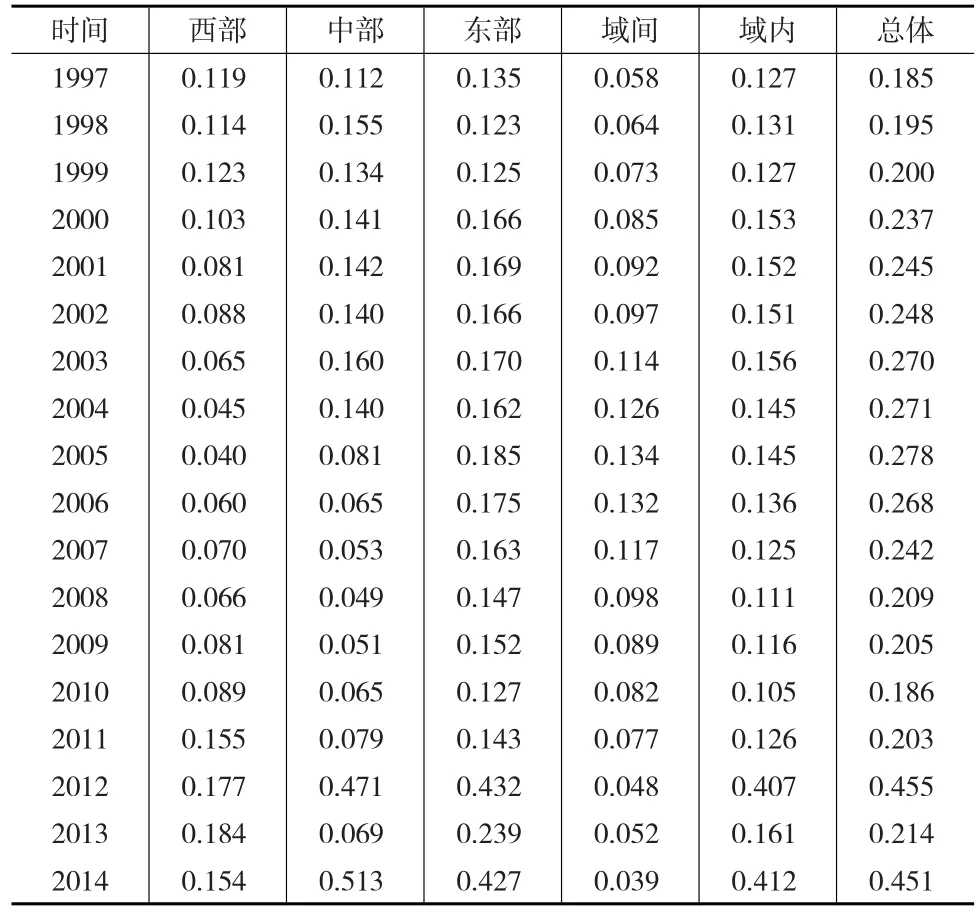
表2 三大区域工业废气排放强度差异
表2显示,从1997—2014年,东、中、西部三大地域内各省份工业废气排放的T0均值分别为0.189、0.146和0.101,这说明和工业废水的区域排放差异类似,东部的工业废气排放不平等程度最高,中西部相对较低。结合资源利用效率进行分析,在整个样本期内,西部平均贡献了全国总体工业产值的12%,排出的工业废气占比为22%;中部平均贡献了全国总体工业产值的26%,排出的工业废气占比为35%;而东部对全国工业产值的平均贡献率最大,达到62%,排出的工业废气占比仅为43%,说明东部的资源利用效率高于中部和西部地区。通过总体差异的双重维度分解结果可知,工业废气排放的区域间差异也始终小于区域内差异,区域内差异表现出增大—减小—增大的N型变动,而区域间差异则表现出先增大后减小的倒U型波动趋势。
此外,三大区域内工业废气排放不平等的波动趋势呈现出阶段性差异。2010年之前,东部各省份工业废气排放差异均值为0.155,中部均值为0.106,西部均值为0.082,三大区域的排放差异在逐渐减小。2010年之后,东部工业废气的排放差异度仍然为三个区域中最高,且东部和中部差异变化基本一致,但西部与东中部差异却随时间变化更加明显。总体而言,西部区域内工业废气排放强度差异变化比较平缓,而东部和中部地区却非常剧烈。

表3 三大区域工业固体废弃物排放强度差异
表3显示,在整个样本观测时期内,东部区域内工业固体废弃物排放不平等均值为0.362,中部均值为0.195,西部均值为0.126。这说明与前两种工业污染排放类似,工业固体废弃物的排放差异从大到小依次为东部、中部和西部,但工业固体废弃物排放与前两种工业污染排放相比,其区域内差异程度更高。此外,结合资源利用效率进行分析可知,在整个样本期内,东部平均贡献了全国工业总产值的62%,而其工业固体废弃物排放量仅占全国总量44%;中部的平均工业产值占比为26%,工业固体废弃物排放量占比为35%;西部的平均工业产值占比为12%,工业固体废弃物占比为21%,因此资源利用率从大到小依次为东部、中部和西部。
从波动趋势来看,2008年以前,东部的工业固体废弃物排放差异均值为0.317,波动变化程度不大;中部均值为0.184,表现出波动下降趋势;而西部均值为0.077,并且和中部的差距在缓慢缩小。2008年后,东部各省份排放强度差异一直保持高持续性增长,均值为0.452。而西部从2009年开始对数离差均值逐渐增大,在2011年首次超过中部并将这种情况持续到2013年,其均值为0.223;中部从2009—2013年有小幅上升但在2014年出现较大增长,均值为0.216。虽然在后面这个时期,中部工业固体废弃物排放差异程度在2014年呈现较大增长但在三个区域内仍然最低,西部的排放不平等则由于2011年的剧烈增加,缩小了其与东部的距离,但却增大了与中部的差异。综合而言,三个区域的工业固体废弃物排放强度差异发生了较为明显的波动。
2.2.2 污染排放强度差异对总体环境不平等的贡献
根据前文,可以计算出区域差异对全国总体工业污染排放差异的贡献,结果见表4。从1997—2014年,中国工业废水排放不平等的域内差异贡献率始终保持在69.8%以上,平均贡献度为87.9%。除去观察期末2014年,域内差异贡献率表现出波动递增状态。域间差异贡献率除在2014年有较大幅度增加外,其他年份却在波动中下降。因此,域内差异是全国工业废气排放总体差异的主要来源。此外分解域内差异可以发现,东部对总体差异的贡献率最低为46.8%,以倒U型先增大后减小;而中西部区域对总差异的贡献最高值分别为32.4%和18.6%。所以,东部区域内各省份工业废水排放不平等既是域内差异的重要原因,也是全国总体排放差异的主要构成因素。

表4 区域差异对总体工业废水排放差异的贡献 (单位:%)
表5的结果显示,从1997—2014年,中国工业废气排放不平等的域内差异的平均贡献度为63.1%,以U型曲线形式先减小后增大,这与工业废水域内差异波动增加的状况极不相同。域间差异则刚好相反,以倒U曲线形式先增大后减小,均值为36.9%。不难看出,域内差异仍然是总体工业废气排放不平等的主要原因。此外在域内差异中,东部区域对总体差异的贡献程度波动非常平缓,在样本期内平均贡献度为43.6%,而中部和西部区域对总体差异的贡献度平均为14.3%和5.2%,且以U型曲线形式先下降后上升。由此可见,工业废气排放不平等的域内差异主要来自东部。

表5 区域差异对总体工业废气排放差异的贡献 (单位:%)
表6显示,在样本期内,工业固体废弃物排放不平等的域内和域间差异平均贡献度分别为78.2%和21.8%,前者波动增加,后者波动降低。域内差异依然是全国总体差异的主要构成因素。与此同时,域内差异主要来自于东部区域内的排放不平等,东部对总体差异的贡献度达到了59.6%。而中西部排放不平等对总体差异的平均贡献分别为14.3%和4.3%,所占比例较小,三个区域对总体差异的贡献程度差异明显。

表6 区域差异对总体工业固体废弃物排放差异的贡献 (单位:%)
3 结论
本文以省域和东、中、西部区域的双重视角,采用不平等指标——广义熵指数及基尼系数,对1997—2014年中国三类工业污染排放的地区差异进行测度分解,得到如下结论:
(1)无论在何种视角下中国地区环境不平等都较为显著,工业污染排放强度呈现出明显的差异性特征。从差异程度上讲,工业固体废弃物排放差异程度最高,工业废气次之,工业废水排放差异程度最低。在波动状态上,在样本期内,各省份工业废水排放与工业废气排放差异的变动状况基本一致,以倒U型曲线形式先升高后降低;而工业固体废弃物却呈现出N型变化。从区域层面上看,东中区域内三种污染物排放强度不平等的变化趋势为N型。而西部工业废水排放强度不平等则表现为倒U型变化,工业废气和工业固体废弃物排放强度不平等表现出U型变化。
(2)对于域内工业污染的排放强度差异,无论对于哪类工业污染物,东部区域内各省份的差异程度最大,中西部区域内的排放差异程度则较小。在1997—2014年的整个观测时期内,东部工业废水排放差异均值为0.106,中部为0.069,西部为0.068;东部工业废气排放差异均值为0.189,中部为0.146,西部为0.101;东部工业固体废弃物排放差异均值为0.362,中部为0.195,西部则为0.126。
(3)分解总体差异可知,全国工业污染排放差异主要来自于域内而非域间。东部是域内差异的主要来源,并且区域内部的环境不平等程度在加剧。需要说明的是,虽然中西部区域内环境不平等程度较低,资源利用程度却较小。东部区域内环境不平等程度最高,但资源利用率却最大,这说明中西部地区有较大的节能空间。
[1]Hedenus F,Azar C.Estimates of Trends in Global Income and Re⁃source Inequalities[J].Ecological Economics,2005,55(3).
[2]Padilla E,Serrano A.Inequality in CO2Emissions Across Countries and Its Relationship With Income Inequality:A Distributive Approach[J].Energy Policy,2006,34(14).
[3]Groot L.Carbon Lorenz Curves[J].Resource and Energy Economic,2010,32(1).
[4]Clarke S A,Qu J,Wang Q,et al.Carbon Inequality at the Sub-nation⁃al Scale:A Case Study of Provincial-level Inequality in CO2Emis⁃sions in China 1997—2007[J].Energy Policy,2011,39(9).
[5]杨俊,王佳,张宗益.中国省际碳排放差异与碳减排目标实现——基于碳洛伦兹曲线的分析[J].环境科学学报,2012,32(8).
[6]李斌,赵新华.经济结构、技术进步与环境污染——基于中国工业行业数据的分析[J].财经研究,2011,(4).
[7]孙耀华,仲伟周,庆东瑞.基于Theil指数的中国省际间碳排放强度差异分析[J].财贸研究,2012,(3).
[8]郑佳佳.区际CO2排放不平等性及与收入差距的关系研究——基于中国省际数据的分析[J].科学学研究,2014,32(2).
[9]赵海霞,王波,曲福田.江苏省不同区域环境公平测度及对策研究[J].南京农业大学学报,2009,32(3).
[10]Shorrocks A,Wan G.Spatial Decomposition of Inequality[J].Journal of Economic Geography,2005,5(1).
