广义半参数趋势混合效应面板模型及其参数估计

殷亮，王维国

（1.大连民族大学理学院与预科教育学院，辽宁大连116650；2.东北财经大学经济学院，辽宁大连116025）

0 引言

在实证分析中，当假设被解释变量的分布为连续型正态分布的情况时，得到经典的线性的计量经济模型，此时模型的预测精度很高。然而，Escribano[1]表明线性的假定过于严格，从大量的经济理论和经济实证中发现，变量之间的关系不都是线性的，Gonzalo等[2]指出，使用经典计量方法研究变量之间的非线性关系时，往往得出错误的结论。因此，基于方法论的拓展和实证分析的需要，学者们将非线性引入到计量模型当中，不仅为计量模型的发展提供了一个方向，也成为计量经济学的前沿热点问题。

有关非线性回归模型的研究，很多成果可以借鉴。从McCullagh和Nelder[3]出版了关于广义线性模型（Generalized Linear Model,GLM）的著作以后，学者们通过各种变换构造广义线性模型对离散的数据进行分析，为非线性模型的发展打下了良好的基础。之后，GLM推广到广义线性混合效应模型（Generalized Linear Mixed Model,GLMM），它既可以对来自非正态分布的数据进行拟合，同时对测量数据和纵向数据模型的内在相关性也可以通过随机效应来刻画，有关广义线性模型的估计方法，McCulloch[4]采用了Monte Carlo Expectation Maximization（MCEM）方法去分析广义线性混合效应模型和广义线性固定效应。

半参数广义线性（SGLM）模型是非线性回归的另一个研究方向，半参数模型的参数部分表示变量间比较确定的线性关系，非参数部分表示不确定的部分。同时此模型假设被解释变量的条件概率分布属于指数分布族，为离散数据及属性数据的分析提供了较好的研究方法。

本文结合Lombardia等[5]的广义半参数趋势混合面板模型和Hunsberger[6]的广义半参数时间模型，建立了广义半参数趋势混合效应面板模型，其解释变量包含非线性时间趋势，为减少其对模型参数估计的影响，结合Robinson[7]和Lombardia等[5]的方法，给出模型的加权极大似然估计量及识别程序。

1 广义半参数混合效应趋势面板模型

广义半参数趋势混合效应模型一方面考虑被解释变量来自指数分布族，另一方面通过假设解释变量包含非线性时间趋势，是半参数广义线性模型的特例，也是半参数趋势面板模型的推广。其形式如下：

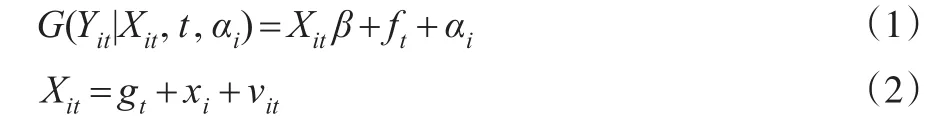
其中，i，t表示横截面单元和时间维度，为了研究方便，本文的Yit是一维被解释变量，Xit是已知解释变量，β(...βd)T是d维未知参数向量，ft=f(t)，gt=g(t)是未知非线性时间趋势函数。严格单调，充分光滑的函数G称为联系函数，给定(X，t，αi)时，Y的条件密度所对应的σ测度设为指数族形式：

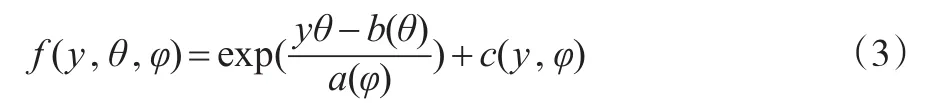
αi，xi是随机效应，这里假定αi～N(0，)，xi～N(0，，vit是平稳的残差序列，vit～N(0，并且限制eit～N(0，表示模型（1）残差向量。同时假定：

在广义半参数趋势混合效应面板模型中，Xit通过ηit=β+ft+αi的半参数形式与Yit建立联系，且半参数ηit=β+ft+αi通过G与Yit的数学期望E(Yit|Xit)相连接，即E(Yit|Xit)=G-1(β+ft+αi)，当G-1为指示函数时，则模型（1）和模型（2）变为半参数趋势随机效应面板模型。

2 广义半参数趋势面板模型的加权似然估计

广义半参数趋势混合效应面板模型估计的主要问题是识别被解释变量Yit和解释变量Xit的关系，本文的模型估计方法是结合Robinson[7]的非参数趋势面板模型的估计方法和加权极大似然估计方法[5]，涉及到极大似然函数的构建问题。因为指数分布族内包含多种分布，被解释变量的不同分布导致了极大似然函数的不同，所以本文分两种情况写出模型的估计方法，第一种是被解释变量来自一般指数分布族，第二种是被解释变量来自指数分布族的一种分布——指数分布。

2.1 被解释变量来自指数分布族

为了表述方便，对模型中变量表示做如下规定：Y∈R，X∈Rp，t∈R，考虑αi是随机影响因素，假设αi～N(0，σu2)，进一步假设残差项=，i=1，...，N，t=1，...，T，令θ=(，δ=(β，θ)，那么对于样本Yit，Xit，t，(i=1，...,N，t=1，...,T)，Yit在Xit和t下的条件概率密度函数为：

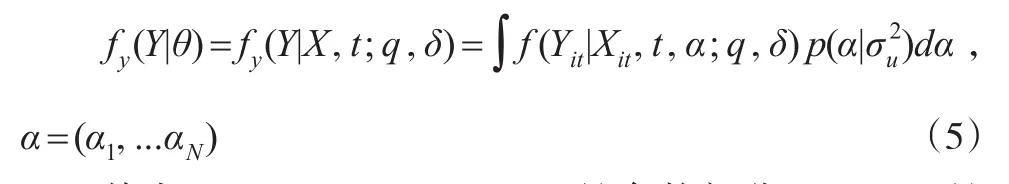
其中，θit=Xitβ+ft+αi，Xβ是参数部分，ft=f(t)是非参部分，是充分光滑的函数，这里，Xit=gt+xi+vit，gt=g(t)也是充分光滑的函数，E(vit)=0p，E()=。

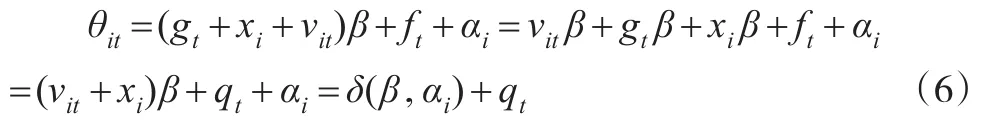
其中，qt=gtβ+ft是依赖于t的非参数部分，δ(β，αi)是依赖β，αi的参数部分，广义半参数趋势混合效应面板模型（1）和模型（2）的主要结果是通过估计加权极大似然函数得到的β，qt=q(t)和αi。

考虑解释变量的非线性时间趋势会对模型的参数估计产生影响，本文提出两步骤对广义半参数趋势混合效应面板模型进行估计。

第一步：采用Robinson[7]提出的非参数趋势面板模型的估计方法，对解释变量Xit进行估计，得到个体效应及非线性时间趋势g=g(t)。即估计模型：

在式（7）中的非线性时间趋势gt，反映解释变量受时间的影响而变化的情况，是非线性的不确定的函数关系，（因为前文设定xi～N(0p，，则E(Xit)=gt），将其代替Xit代入θit中，得到：

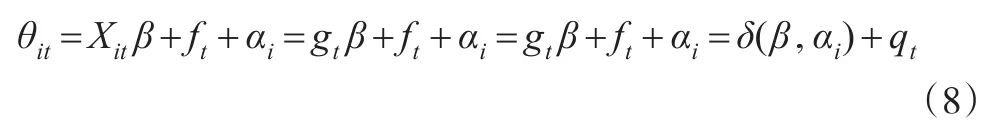
其中，依赖β，αi的参数部分是δ(β，αi)，依赖于t的非参数部分qt=ft，通过估计加权极大似然函数得到β和q(t)=f(t)为广义半参数趋势混合面板模型（1）和模型（2）的主要结果。

第二步：采用加权极大似然估计方法估计模型的参数和非参数估计量。

模型的估计问题主要是识别参数，即参数部分β和αi，非参数部分qt=ft是本文要估计的，由后验分布可知：

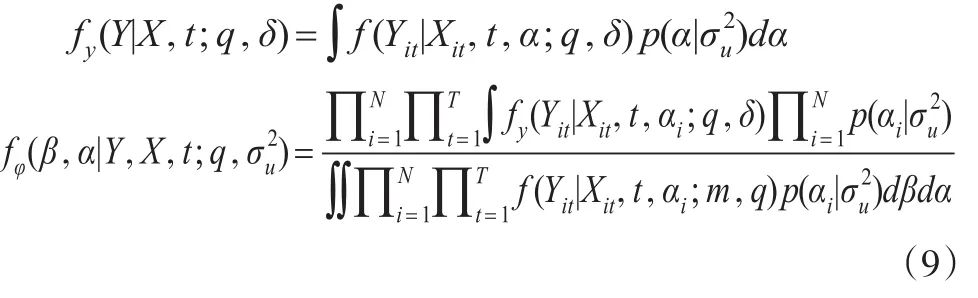
根据极大似然估计的思想，估计的参数β和αi能使得式（9）值达到最大，只需保证分子达到最大即可。定义：

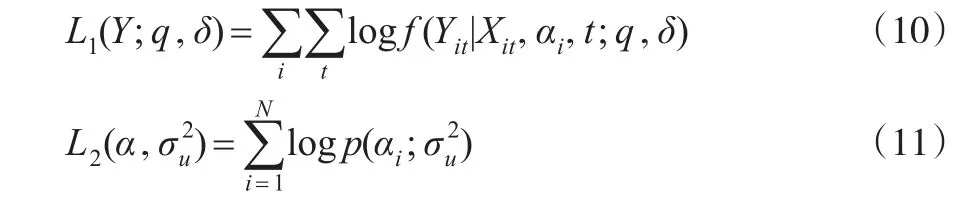
令L(Y，α;q，δ)=L1(Y;q，δ)+L2(α，，为了估计非参数部分qt=ft，本文固定t0点，计算t0点的Y的对数条件密度函数：

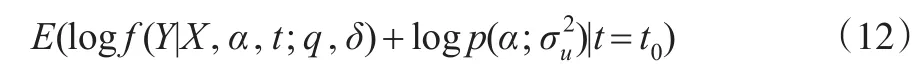
则加权极大似然函数为：

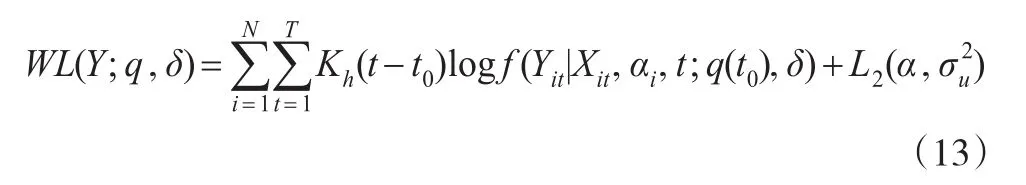
其中，Kh(t0)=K(t-t0h)是带宽为h的核函数，满足在[-1，1]上的lipschitz对称概率密度函数。

为表示方便，计算：

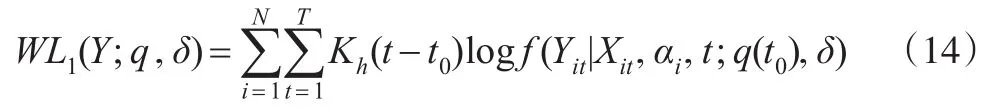
此式称为加权极大似然函数，其解为加权极大似然估计量。

2.2 被解释变量服从指数分布

为了使上面的估计方法具体化，选择指数分布作为指数分布族的一类分布，当被解释变量服从指数分布时：其概率密度函数为λe-λy，其中，λ=1 E(Y)，首先给出广义半参数趋势混合面板模型的形式，令模型的半参数部分为ηit=Xitβ+ft+αi，被解释变量的数学期望为E(Yit|Xit)=μit，二者通过G建立联系，即G(μit)=ηit=Xitβ+ft+αi，其中，严格单调充分光滑的G函数称为联系函数。h=G-1，即μit=h(ηit)=1/ηit，或G(μit)=1 μit。此时模型（1）和模型（2）变为：

当被解释变量服从指数分布时，借鉴上面给出的模型估计方法的一般情况，得到似然函数形式如下：

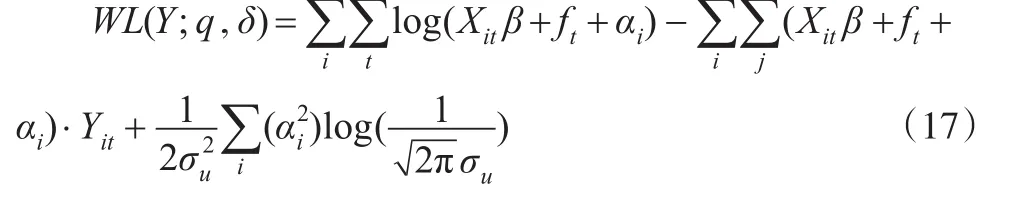
则其加权似然函数为：

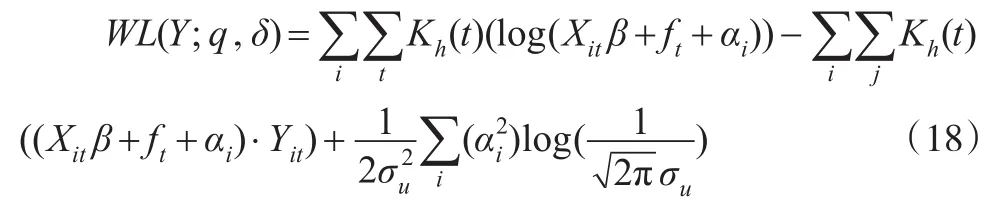
将采用Robinson的方法对解释变量的非线性时间趋势进行分离，将其代替解释变量代入到加权似然函数当中，得到：

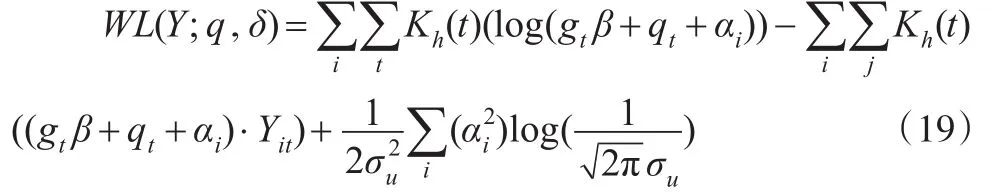
其极大似然估计量为∂WL(Y;q，δ)/∂β=0，求出被解释变量服从指数分布时的广义半参数趋势混合面板模型的参数估计量和非参数估计量。

3 最优化算法

半参数趋势随机效应面板模型的参数和非参数估计量是加权似然函数的最优解，然而它是非显示解。本文参考Lombardia和Sperlich[5]提出的算法，对其进行估计。

步骤1：对于固定时间的t0，当给定参数δ（β和αi）时，可以通过下式估计非参数部分q(t0)：

步骤2：结合式（20）结果，可以通过下式估计估计β和αi：

4 蒙特卡罗数值模拟

本文与Lombardia和Sperlich[5]不同的地方是除了考虑被解释变量是包含时间趋势的非平稳变量，解释变量也是如此。如果直接参考Lombardia和Sperlich[5]提出的估计方法估计模型的参数和非参数估计量，解释变量的时间趋势可能对估计方法产生影响。为了验证猜想，本文首先考虑解释变量是不含时间趋势的平稳变量，生成数据，对Lombardia和Sperlich[5]的估计方法进行验证，然后，考虑解释变量包含非线性时间趋势，生成数据，对本文提出的估计方法和Lombardia和Sperlich[5]提出的估计方法进行对比分析。

4.1 生成数据

为了研究方便，在此部分假定Xit为一维变量，则广义半参数趋势混合效应面板模型形式如下：

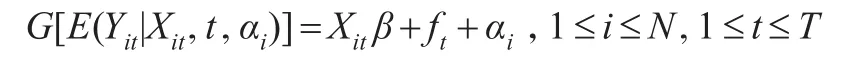
其中，Yit来自指数分布族，因为指数分布族中的分布的形式过多，同时与上面的估计方法相对应，所以本文基于指数分布族中的一类分布——指数分布给出广义半参数趋势混合效应面板模型的加权极大似然估计方法，在此部分，选用指数分布作为指数分布族的特殊分布给出数据生成过程。

（1）非线性时间趋势：本文中非线性时间趋势是被解释变量和解释变量非平稳的主要原因，f(u)=2u3+u，g(u)=2sin(πu)，k(u)=2πu为非线性的时间趋势，反映了政策、法律、法规等随机因素对变量的影响。

（2）随机效应：面板数据中，对于特定的个体而言，随机效应是不随着时间发生改变的影响因素。αit在N(0，0.25)的正态分布中随机抽取，xit在N(0，1)的正态分布中随机抽取。

（3）残差项：eit在N(0，0.25)的正态分布中提取，序列独立的序列。vit在N(0，0.6)的正态分布中提取。

（4）解释变量与被解释变量：本文的特别之处就在于考虑了解释变量是因包含非线性时间趋势而非平稳的变量。在数据生成部分，按照两种情况来生成解释变量Xit，一种是平稳变量，服从正态分布N(1，0.6)，不包含个体效应和时间趋势，另一种是包含时间趋势的非平稳变量，按照Xit=vit+xi+gt生成。在接下来的蒙特卡罗模拟中，考虑解释变量的时间趋势，加入g(u)=2sin(πu)及k(u)=2 πu，被解释变量Yit按照指数分布来生成，即：

其中，Yit是以E(Yit)=1/Xitβ+αit+ft为期望的指数分布生成，ft的形式是按照g(u)及k(u)来构造。

4.2 广义半参数模型蒙特卡罗数值模拟

按三部分进行模拟实验：第一，是验证Lombardia和Sperlich[5]提出的估计方法，第二，从标准差的角度对比分析本文的估计方法和Lombardia和Sperlich[5]的估计方法，第三，从均方误差的角度对比分析本文的估计方法和Lombardia和Sperlich[5]的估计方法。

（1）首先验证Lombardia和Sperlich[5]的估计方法，即对广义半参数混合效应面板模型的参数估计量和非参数估计量进行估计，分析其有限样本性质。

为了使实验更一般化，在蒙特卡罗模拟部分，对模型参数进行两种假定，即假设模型参数分别为β=3和β=5的情况及随机效应的分布方差为=0.0625和=0.09的情况。

考虑到时间维度或截面维度的变化会对广义半参数混合效应面板模型的参数估计产生影响，首先固定时间维度不变，增加截面维度。观察模型参数估计变化情况。然后固定截面维度不变，增加时间维度，观察模型参数估计变化情况。

取T=5保持不变，N增加（N=10、N=15、N=20、N=25、N=30），进行500模拟，计算500次模拟参数估计值的平均值和标准差。为了另取一时间维度不变，增加截面维度，即取T=10保持不变，N增加的情况（N=10、N=15、N=20、N=25、N=30）的情况。进行500次模拟，计算500次模拟参数估计值的平均值和标准差。结果如表1和表2所示。

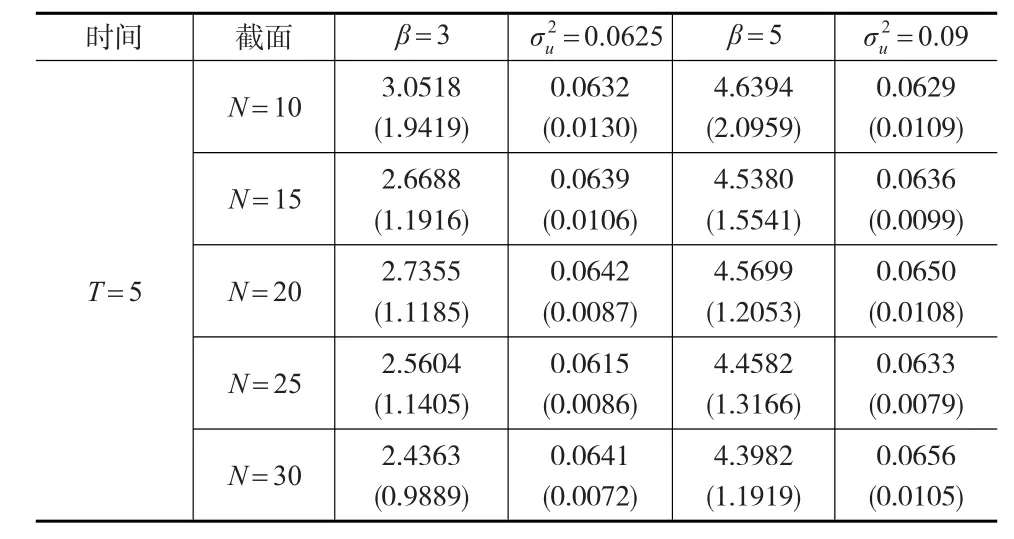
表1 广义半参数混合效应面板模型参数估计结果（T=5）

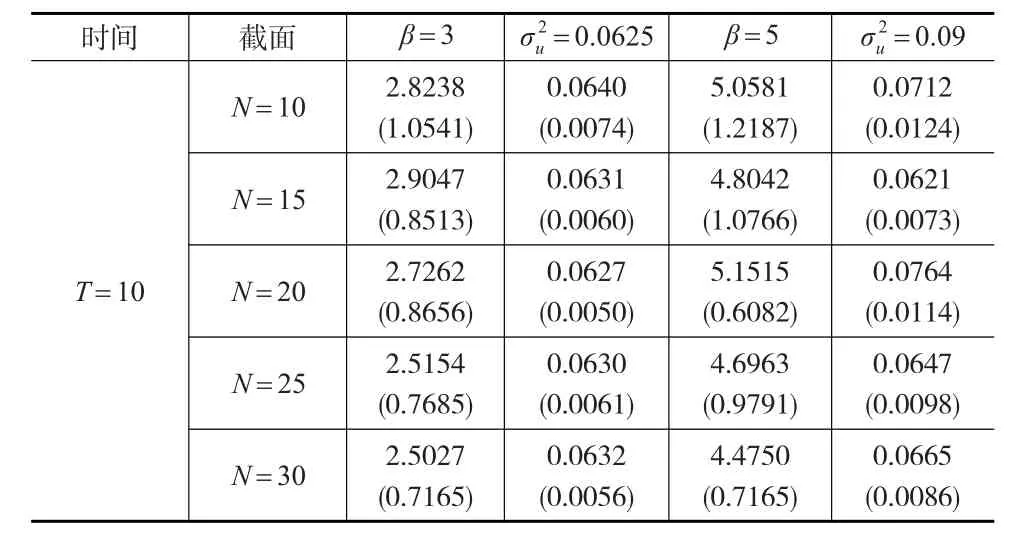
表2 广义半参数混合效应面板模型参数估计结果（T=10）

表1和表2列出了广义半参数混合效应面板模型的参数估计情况，随着样本容量的变化，其有限样本性质如下：

当保持时间维度T不变时，增加个体数N，广义半参数混合效应面板模型的参数估计结果有如下特征。第一，模型的参数估计值的均值变化比较稳定。比如，在假定β=3的情况下，保持时间维度T=10不变，N=15时参数估计值最接近真实值。第二，除个别情况下（T=5，N=25；T=10，N=15），随着截面个数N的增加，参数估计值的标准差有逐渐减小的趋势。比如，在β=5，T=5的情况下，随着个体数N的增加（N=10、N=15、N=20、N=25、N=30），参数估计值的标准差在逐渐减小。第三，随机效应分布的方差估计的结果较为理想，在β=3和β=5的假定下，其方差估计的结果较为准确。

当保持截面维度N不变，增加时期数T（从T=5到T=10）时，广义半参数混合效应面板模型的参数估计结果有如下特征。第一，模型的参数估计值的均值变化的稳定性提高，即在T=5下的情况下，β=3的均值变化幅度较大，而在T=10时，其均值变化比较稳定。第二，模型参数估计值的标准差在逐渐减小，即在T=5时，β=3的参数估计值的标准差在0.9～1.9之间，而在T=10时，β=3的参数估计值的标准差在0.7～1.1之间。第三，估计的随机效应分布的方差结果较为理想，在β=3和β=5的假定情况下的假定情况下，模型的随机效应方差估计的结果都比较准确。

（2）表1和表2是在假设解释变量为平稳的变量的情况下得到的结论，验证了广义半参数混合面板模型的有限样本性质，下面考虑解释变量为包含时间趋势的非平稳变量时，对比分析Lombardia和Sperlich[5]提出的广义半参数混合效应面板模型估计方法和本文提出的两步骤模型估计方法。表3和表4表明Lombardia和Sperlich[5]提出的方法的估计结果。

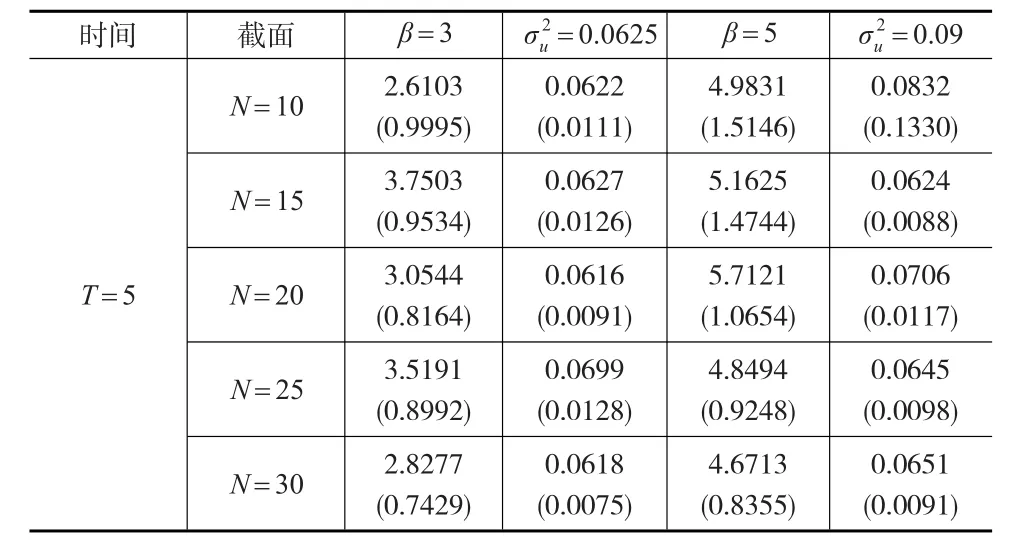
表3 广义半参数趋势混合效应面板模型参数估计结果（T=5）

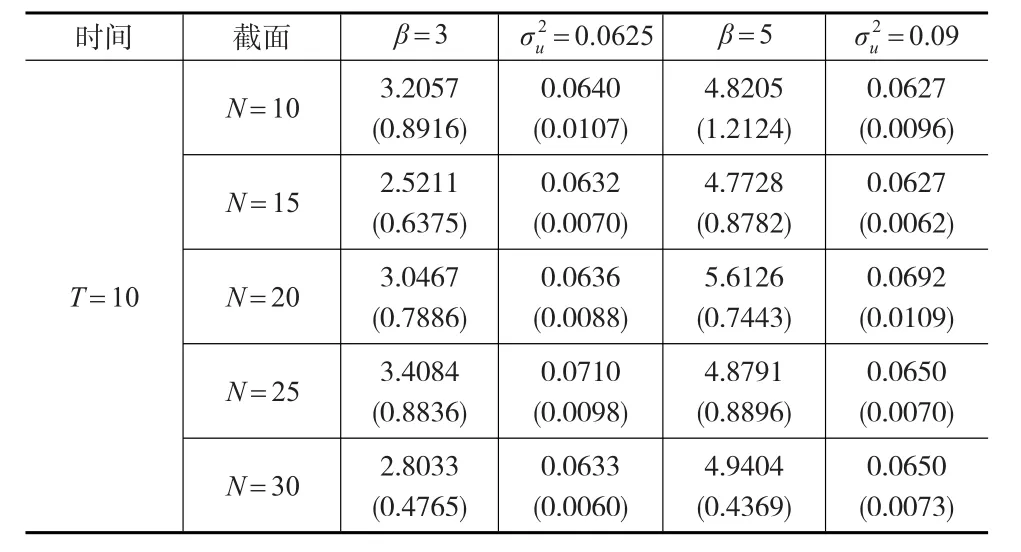
表4 广义半参数趋势混合效应面板模型参数估计结果（T=10）

从表3和表4的参数估计结果发现，当解释变量是含有非线性时间趋势的非平稳变量时，采用Lombardia和Sperlich[5]提出的极大似然估计方法估计广义半参数趋势混合面板模型的参数，参数估计结果较好。第一，随着样本容量N、T的变化，参数估计值变化比较稳定。第二，除个别情况下，随着样本容量N、T的变化，参数估计值的标准差有逐渐减小的趋势。第三，随机效应分布的方差估计结果较为理想。

尽管Lombardia和Sperlich[5]提出的极大似然估计方法依然可以对广义半参数趋势混合面板模型参数进行估计，然而，由于解释变量从平稳变量变成包含时间趋势的非平稳变量，Lombardia和Sperlich[5]提出的极大似然估计方法是否是最佳的？是本文需要研究的问题。接下来，采用本文提出的两步骤估计方法对广义半参数趋势混合面板模型进行估计，即首先采用Robinson(2012)[7]提出的非参数趋势面板模型估计方法对解释变量的时间趋势进行分离，然后用其代替解释变量代入到广义半参数混合效应面板模型当中进行加权极大似然估计，观察估计结果。如表5和下页表6所示。

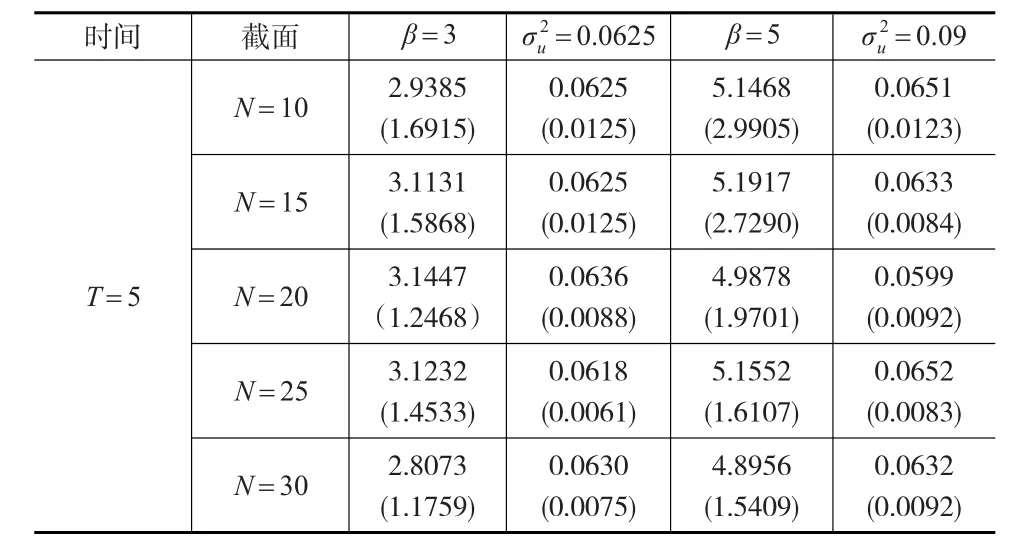
表5 广义半参数趋势混合效应面板模型参数估计结果（T=5调整）

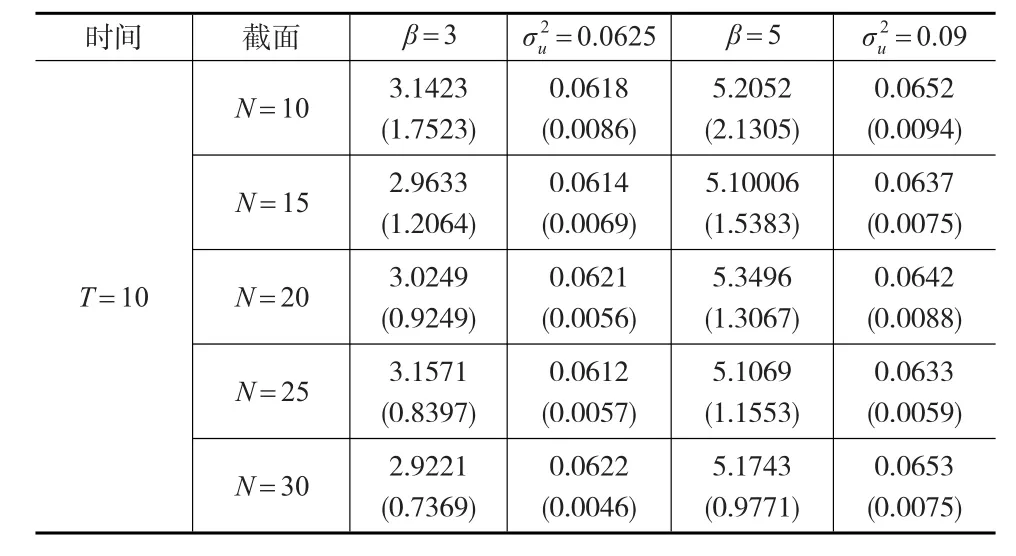
表6 广义半参数趋势混合效应面板模型参数估计结果（T=10调整）

从表5和表6与表3和表4的估计结果发现：当解释变量是包含时间趋势的非平稳变量时，本文提出的两步骤估计方法与Lombardia和Sperlich[5]提出的加权极大似然估计方法对比结果如下：从共同点来说，除个别情况下，两种参数估计结果都保持了参数估计值变化比较稳定，估计值的标准差随着样本容量的增大而减小的特征。从不同点来说，若直接采用广义半参数模型进行分析采用加权极大似然法估计，参数估计值均值估计较稳定的情况下，参数估计值的标准差结果好于先对解释变量进行分离然后再进行加权极大似然估计的估计结果，后者均值的标准差在整体水平上有明显的增大趋势。

（3）从以上两种方法的估计结果来看，参数估计值均值变化都较稳定，本文提出的估计方法的参数估计值的标准差虽然在整体水平上略大于Lombardia和Sperlich[5]提出的方法，但是相差不大。仅从估计值的标准差大小来判断两种估计方法哪个更可靠，不够客观，下面计算两种估计方法的估计值的均方误差，观察计算结果，进一步比较两种估计方法的优良。

对于参数β的估计值的均方误差计算公式如下：

均方误差刻画的是估计值的损失函数，均方误差越小，估计效果越好。为了清楚地对比两种方法均方误差的大小，下面列出β=3时，两种估计方法的参数估计值的均方误差，用L(2008)表示采用Lombardia和Sperlich[5]提出的加权极大似然估计方法，用L&R(2012)表示本文提出的估计方法，即先采用Roinson[7]对解释变量X的时间趋势进行分离，然后采用加权极大似然法进行估计。计算结果见表7。从表7的结果可以看出，本文提出的估计方法的参数估计值的均方误差略小于Lombardia和Sperlich[5]提出的加权极大似然估计方法。

表7 参数估计值的均方误差

5 结论

本文在Lombardia和Sperlich[5]和Hunsberger[6]的基础上，建立了解释变量为包含时间趋势的广义半参数趋势混合效应面板模型，并给出加权极大似然估计的有效估计量及识别程序。在仿真实验部分中，当被解释变量服从指数分布时，对于解释变量为非平稳的时间序列，本部分采用了Lombardia和Sperlich[5]提出的加权极大似然估计方法和本文提出的估计方法进行对比分析了两种估计方法的估计结果。

两种估计方法得到的参数估计结果较为理想，都保持了参数估计值变化稳定，估计值的标准差随着样本容量增加而减小的特征。从参数估计值标准差上来看，本文提出的估计方法的参数估计值的标准差略大于Lombardia和Sperlich[5]提出的加权极大似然估计方法的标准差，从均方误差来看，本文提出的估计方法的均方误差略小于加权极大似然估计方法的均方误差。

[1] Escribano A.Nonlinear Error Correction:The Case of Money Demand in the UK(1878-2000)[J].Macroeconomic Dynamics，2004，(8).

[2] Gonzalo J,Pitarakis J Y.Threshold Effects in Cointegrating Relationships[J].Oxford Bulletin of Economics and Statistics,2006，(68).

[3] McCullagh P,Nelder J A.Generalized Linear Models(second edition)[M].London:Chapman and Hall,1989.

[4] McCulloch C E,Natarajan R.A Note on the Existence of the Posterior Distribution for a Class of Mixed Models for Binomial Responses[J].Bimometrika，1995，(82).

[5] Lombardia M J,Sperlich S.Semi-parametric Inference in Generalized Mixed Effects Models Working Paper[J].Journal of the Royal Statisti⁃cal Society,2008,70(5).

[6] Hunsberger S.Semi-parametric Regression in Likelihood-Bsed Mod⁃els[J].Journal of the American Stastical Association,1994,89,(428).

[7] Robinson P M.Non-parametric Trending Regression With Cross-sec⁃tional Dependence[J].Journal of Econometrics,2012,(169).