Surfer软件在三角形组合喷灌均匀度计算中的应用
2018-03-21毕庆生顿文涛叶卫东
毕庆生,李 波,顿文涛,叶卫东
(1.河南农业大学资源与环境学院,郑州 450002;2.河南农业大学网络中心,郑州 450002)
水肥一体化喷灌系统设计的关键技术指标之一是组合喷灌均匀度,它即涉及灌水质量,也涉及施肥的均匀度和项目建设的资金投入,因此,《喷灌工程技术规范》(GB/T50085-2007)规定,“定喷式喷灌系统喷灌均匀系数不应低于0.75”[1]。在具体工程设计中,由于测试和计算复杂、工作量大,很少计算喷灌均匀度,喷头的布置主要是采用几何组合法、修正几何组合法和经验系数法等布置方法。由于喷头种类繁多、性能差异很大,对具体工程项目而言,按此方法布置结果有时并不十分理想。为此,一些学者就均匀度的计算开展了一些研究。杨路华[2]等(2004年)利用Surfer软件计算了喷(微)灌在喷头间距等于或小于喷洒半径情况下的均匀度;河北农业大学的张志宇[3](2006年)运用Matlab径向神经网络研究了基于径向基模型的组合喷灌均匀系数的计算,然后通过遗传算法进行组合最优化,得出最优组合间距;劳冬青、韩文霆[4](2010年)通过接口软件MATCOME4.5,结合Matlab与Visual C+ +工具混合开发出喷头水量分布仿真及组合优化软件系统;西北农林科技大学的张洋[5](2012年)以C#和OpenGL为开发语言,开发了一套集喷头水力性能和喷灌系统评价的软件系统,可以计算出给定的任意组合形式和组合间距进而求得组合均匀度。刘晓阳[6]等(2016年)采用矩阵叠加方法,利用Surfer软件和Matlab计算微喷灌的均匀度,对微喷头水量分布仿真及组合优化研究。这些方法无疑都是可行的,但是,这些方法要么需要自己编程,要么只能计算喷头间距不大于喷洒半径情况下的组合均匀度,在利用目前流行的应用软件来计算喷灌均匀度方面研究还不够。
Surfer软件以其强大的插值功能和绘制图件能力在地质、气象、水文等领域得到广泛的应用,已成为用来处理X、Y、Z数据的流行软件。本文以单喷头喷洒试验数据为基础,利用单喷头水量分布叠加原理,通过对单喷头喷洒区域的虚拟扩展,以及典型代表区域和计算区域的设定等,利用流行的Surfer软件的坐标变换、数据处理,以及excel软件的统计公式计算喷头三角形布置形式下各种不同间距组合喷灌均匀度,并通过算例对数据网格化插值方法及其数据间距跨度进行了分析。
1 三角形组合喷灌典型代表区域和计算区域的设置
1.1 典型代表区域设置
在进行喷灌设计时,一般一个地块选用的喷头都是同一品牌和同一型号,喷头性能一致(不考虑喷头制造的差异情况下),在整个喷灌区域按照一定方式均匀布置,因此,在计算喷灌均匀度时一般选取一个代表性区域进行计算,无需计算整个区域,该选取的代表性区域即为典型代表区域。对于三角形喷头布置而言,最常见的是选择相邻3个喷头包围着的三角形区域作为典型计算区域。如图1阴影部分所示。

图1 喷头三角形组合布置示意图
考虑投资要求,喷头间距不宜太小,生产中一般情况下大于喷洒半径R的一半;但也不能太大,否则会发生漏喷现象。如图1所示,设喷头沿支管间距为a,支管间距为b,喷洒半径为R,则不发生漏喷的临界状况是喷头p1、p2、p4以射程为半径的园相交于典型计算区域中的O点,因此,不发生漏喷的条件是(a2+4b2)/8b≤R。
根据喷头间距大小和喷头喷洒半径大小,它涉及3个或5个相邻喷头,如图1所示,当喷头p3、p5的喷洒半径R小于其距离三角形代表区域边线的距离时,对典型代表区域而言就只有3个喷头有效喷洒,否则即为5个喷头有效喷洒。
1.2 坐标系统建立与喷头坐标位置的确定
为了便于计算,建立直角坐标系,将典型计算区域相关的喷头位置布置在同一坐标系中,如图1所示。结合Surfer软件特点,选取左下角喷头p2位置为原点,其他喷头坐标按照喷头布置位置和间距计算确定。各喷头坐标见表1。

表1 三角形布置各喷头坐标
注:a为喷头沿支管间距,m;b为支管间距,m。
1.3 单喷头喷洒区域的虚拟扩展
Surfer软件数据处理时其操作区域形状为矩形。单喷头测试数据经Surfer软件网格化处理后,计算区域变换为以喷头为中心,2倍喷射半径为边长的正方形。这样的话,不同的喷头在典型计算区域只是覆盖了部分不同的区域,如图1所示。要计算典型计算区域上的各个喷头的叠加水量就要把典型计算区域分割成不同形状的小区域计算,计算非常麻烦,不能很好地发挥Surfer软件的计算功能。为此,考虑将单喷头的覆盖区域进行虚拟扩展,扩展后喷洒半径以内区域为真实区域,其喷洒水量大于0,喷洒半径之外区域为虚拟扩展区域,其喷洒水量为0。考虑到实际喷灌系统设计中喷头间距最大不会大于2倍的喷洒半径,否则就会出现漏喷现象。可将扩展后的区域确定为以4倍喷洒半径为边长的正方形区域。如图2所示。扩展后,所有相关喷头都可以对典型计算区域全覆盖,不需要将典型计算区域划分为不同的扇形、弓形区域等,只需要对典型计算区域进行整体处理即可,只不过真实覆盖区域喷洒水量大于0,虚拟扩展区域喷洒水量为0,典型计算区域所得水量分布仍为相邻多个喷头喷洒水量分布之和,这样就满足Surfer软件数据处理区域为矩形区域的规定,极大地简化了计算工作量。

图2 喷头喷洒面积与扩展面积示意图
1.4 计算区域设置
由于Surfer软件直接计算操作的区域为矩形区域,而典型代表区域为三角形区域,不能直接计算,因此,在对三角形典型代表区域计算前,首先设计一个包含全部三角形典型计算区域的矩形区域作为计算区域,如图3所示。先对该矩形区域进行数据计算处理,然后再通过三角形典型代表区域白化处理,计算三角形代表区域的喷灌均匀度。计算区域可按图3所示,选取p1、p2喷头为下顶角,以a、b为边长设置,覆盖三角形典型代表区域。

图3 矩形计算区域示意图
2 多喷头三角形组合形式下的均匀度计算步骤
在前文单喷头虚拟拓展、典型代表区域和计算区域设置的基础上,将单喷头测试数据利用Surfer软件对数据进行网格化处理、图形叠加和相应叠加部分的数据提取及转换等一系列的数据处理,可简便的计算出典型计算区域喷洒水量分布数据,然后利用excel软件数据统计公式计算喷灌组合均匀度,具体步骤如下。
第1步,以喷头为中心,将单喷头测试数据计算区域虚拟扩展边长为4倍喷洒半径的矩形区域。如果是按照径向射线布置测试数据,可视其为极坐标数据并转化为直角坐标数据,然后分别沿X轴、Y轴方向增加数据点,可在excel文件中,以喷头位置为中心,将X、Y的坐标范围扩大到4倍喷洒半径,其虚拟扩展部分的喷洒水量值Z设为0。
第2步,单喷头测试数据网格化处理。利用Surfer 11软件进行单喷头测试数据网格化处理,生成.grd格式文件。在网格化数据对话框中,数据插值方法可选用最近邻点法、克里金法、自然邻点法等几种插值法,选择数据间距后即可进行网格化处理。
第3步,单喷头测试数据去负值处理。在进行单喷头测试数据网格化插值的过程中可能会产生负值,显然这是不合理的,因为喷洒量不可能为负。我们可利用Surfer软件math计算功能的max(a,0)函数,将格式化中产生的负值变为0。这样处理的结果既保证了数据非负,也较好地维持了平滑插值的特点。
第4步,不同喷头位置坐标计算。多喷头组合喷洒,相当于单喷头在不同位置喷洒的叠加。利用Surfer软件的transform功能,在transform对话框中设定相应的坐标变换数据,参看图1和表1。经过坐标换算,逐一得到不同位置喷头的坐标值,相应的,也得到不同位置的单喷头喷洒水量分布数据。
第5步,各喷头矩形计算区域喷洒水量数据提取。各喷头位置不同,其对应于矩形计算区域的喷洒水量分布值也不同。对应矩形计算区域,利用Surfer 11软件的extract功能,在}对话框中设置矩形计算区域X、Y坐标范围,逐个喷头提取矩形计算区域喷洒水量分布值,并逐个保存为.grd格式文件。
第6步,矩形计算区域喷洒水量数据叠加(合并)计算。利用Surfer 11软件的math计算功能中的数据相加函数,计算对应矩形计算区域的叠加喷洒水量值,并生成叠加后的.grd格式文件。
第7步,设置典型计算区域.bln格式白化文件。有两种方法,一是可以在Surfer的plot场景下,在上述叠加水量文件生成的等值线图上利用数字化功能选取典型计算区域并生成.bln格式白化文件;二是在工作表上直接输入三角形典型计算区域各个顶角的坐标值,并保存为.bln格式白化文件。
第8步,利用blank命令和三角形典型计算区域的.bln格式文件,对第6步矩形计算区域叠加后的.grd文件进行白化处理,生成三角形典型计算区域白化后的.grd文件。
第9步,将典型计算区域白化后的.grd文件格式数据转换为.dat格式数据文件。在Surfer 11软件中,利用convert命令打开典型计算区域白化后的.grd格式的数据文件,另存为.dat格式数据文件即可得到三角形典型代表区域水量分布数据。
第10步,在excel软件中打开转换后的.dat数据文件,并将其中三角形典型计算区域以外的点去除,即将Z值(一般为C列)等于1.70E+38的行删除,然后对剩下的即三角形典型代表区域以内的有效点进行喷洒水量均匀度计算,得出不同喷头组合下的均匀度值。
这里,喷灌均匀度选用克里斯琴森系数[7]表示。算式如下:
(1)

3 算例与讨论
单喷头实测数据选用李小平博士论文《喷灌系统水量分布均匀度研究》[8](2005年)中的测试资料,测试条件为:①喷头型号:PY-20。②试验工作压力:350 kPa。③试验条件:风速0.3 m/s。④量雨桶布置如图4所示:雨量桶按8条径向射线“米”字形布置,第一个量雨桶到喷头中心间距为1 m,其余量雨桶间距为2 m,每条射线上12个测点。测试数据见表1。

图4 单喷头实验水桶布置示意图(单位:mm/h)
3.1 不同数据网格化插值模型有效性比较
Surfer 11提供了12种数据网格化插值模型,分为精确插值和平滑插值两类,经过分析,对喷灌均匀度计算而言比较适合的方法主要有克里金法(Kriging)、线性插值三角网法(Triangulation with Linear Interpolation)、最近邻点插值法(Nearest Neighbor)、自然邻点插值法(Natural Neighbor)4种,现对这4种网格化插值方法进行比较。
按照互有效性原理,采用交叉验证方法[9],即对第一象限即II射线12个测点(见图4)实测值与网格化插值预测值进行比较,分别计算其残差、平均估计误差百分比(PAEE)、相对均方差(RMSE),对各种模型进行有效性评价。结果见表2和表3。
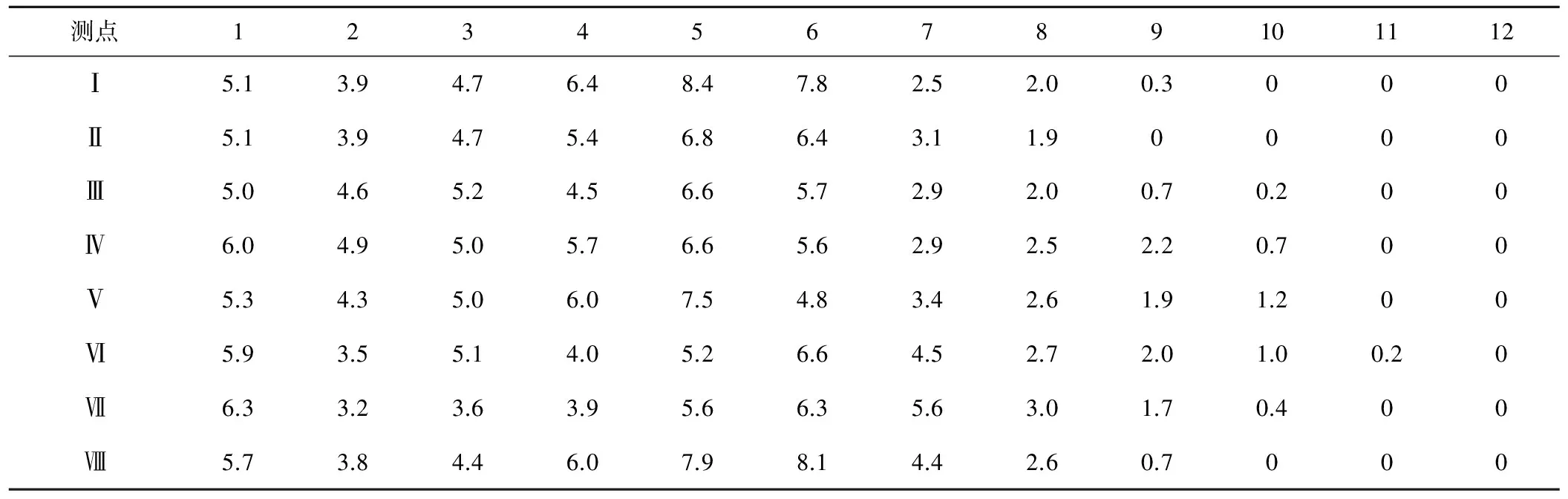
表1 射线法测量数据 mm/h

表2 各测点不同插值模型的残差 mm/h
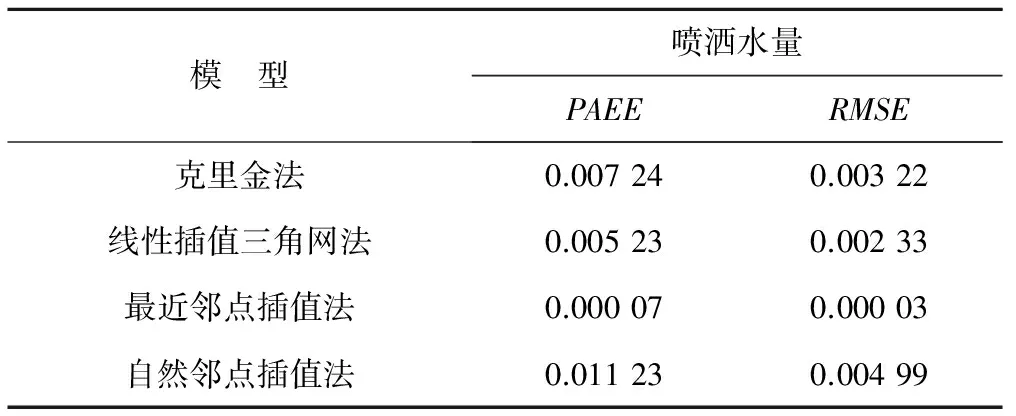
表3 各插值方法有效性比较 mm/h
通过12个测点不同插值模型的残差、平均估计误差百分比(PAEE)、相对均方差(RMSE)计算,结果表明最近邻点插值法残差、PAEE、RMSE均最小,因此,比较而言,4种插值模型中最近邻点插值法有效性好于其他模型,其次是线性插值三角网法、克里金法,自然邻点插值法有效性最差。
3.2 数据网格化跨度对均匀度计算的影响分析
按照上述方法步骤,采用最近邻点插值法对原始数据进行不同网格化跨度和喷头间距组合计算均匀度,计算结果见表4。数据网格化跨度取0.5、1.0、2.0这3个水平,喷头沿支管间距和支管间距分别为20×20、24×24、28×28这3种组合。

表4 不同喷头间距、不同数据网格跨度三角形组合形式下喷洒均匀度Cu %
注:a为喷头沿支管间距,m。b为支管间距,m。
从计算结果来看,在0.5~2.0的范围内,数据网格化跨度对均匀度计算影响很小。但是,根据典型代表区域确定规则,三角形典型代表区域边线应为一直线,由于计算中采用的是网格化处理方法,典型代表区域的边线实际为锯齿形折线。在Surfer软件白化处理时折线区域全部白化掉了,使得计算区域仅为折线内部的区域,比选定的典型代表区域要小,数据网格跨度越大,折线区域越大,实际计算区域比典型代表区域小的就越多;另外,当数据网格跨度不是所有相关喷头坐标的整倍数时,也存在各个喷头的计算区域错位现象,算例中为规避这一问题选取典型喷头间距。因此,在喷头和支管间距为整数时,建议数据网格跨度取0.5较为合适,虽然数据计算量大一些,但降低了三角形边线的折线幅度,消除了各个喷头计算区域错位现象,计算结果更可信。
4 结 语
(1)进行喷洒面积虚拟拓展可解决喷头间距大于喷洒半径时不同喷头喷洒面积叠加部分不规则的问题,使得应用Surfer软件快速计算喷灌均匀度得以简化而成为可能。
(2)应用Surfer 11软件计算喷灌均匀度时可以使用多种插值模型,交叉验证结果显示最近邻点插值法有效性明显好于其他模型。
(3)数据网格式化时的数据跨度间距对计算结果没有太大影响,但考虑到尽可能降低三角形边线的折线幅度,消除各个喷头计算区域错位现象,采用0.5的跨度间距更合适。
[1] GB/T50085-2007,喷灌工程技术规范[S].
[2] 杨路华,刘玉春,柴春玲,等.应用Surfer软件进行喷(微)灌均匀度分析[J].节水灌溉,2004,(5): 14-16.
[3] 张志宇.喷头水量分布的智能仿真与组合间距的优化[D].河北保定:河北农业大学,2006.
[4] 劳冬青,韩文霆.喷头水量分布仿真及组合优化软件系统研究[J].节水灌溉,2010,(1):42-45.
[5] 张 洋.基于C#与OpenGL喷头水量分布动态模拟及组合优化[D].陕西杨凌:西北农林科技大学,2012.
[6] 刘晓扬,杨路华,柴春岭,等.微喷头水量分布仿真及组合优化研究[J].节水灌溉,2016,(3):24-26.
[7] 王春堂.农田水利学[M].北京:中国水利水电出版社,2014.
[8] 李小平.喷灌系统水量分布均匀度研究[D]. 武汉:武汉大学,2005.
[9] 白世彪,王 建,常直杨.Surfer10地学计算机制图[M]. 北京:科学出版社,2012.
