基于Copula函数的区域作物生育阶段干旱频率分析
2018-03-21陈海涛李阿龙
陈海涛,邱 林,李阿龙
(华北水利水电大学水利学院,郑州 450011)
我国北方大部分区域,农业干旱问题突出,分析研究区域农业干旱特征,对于加强对干旱的预防和应急管理,促进区域水资源的合理配置具有重要意义[1,2]。
以往针对干旱事件的研究往往采用游程理论从长期实测资料中提取干旱指标(如干旱研究中常用的干旱历时、干旱烈度、干旱强度等),然后进行Copula拟合,从而分析研究区域的干旱分布状况。Copula函数不受各单变量边际分布类型的影响,可以方便地用于构建变量联合分布模型,目前在水文事件多元频率分析中得到了广泛应用。闫宝伟等[3]应用Copula函数分别构造了最大洪水发生时间及发生时间与其量级之间的联合分布;冯平等[4]采用Gumbel Copula构造降雨量和入境水量的联合分布;刘曾美等[5]采用Copula函数构建了区间暴雨和外江洪水位的联合分布模型;Genest和Favre[6]基于Copula函数建立洪峰洪量联合分布模型。在干旱研究方面,Copula函数也有大量的应用并取得一定成果,周玉良等、陆桂华等……采用Copula进行区域水文干旱频率、分布研究[7-11];陈永勤等[12]、李记等[13]采用Copula函数进行了流域干旱频率分析;于艺等[14]采用Copula函数进行多变量干旱特征分析;孙可可[15]等结合Copula函数建立抗旱能力指数与干旱频率的对应关系,得到实际抗旱能力下的农业旱灾损失风险曲线。
以往的方法在系统刻画研究区域干旱特性,分析区域水文干旱、气象干旱特性方面作用显著。但由于作物不同生育阶段生长需水量存在差异,而不同生育阶段缺水对作物产量影响也不相同,而上述方法不能得出作物不同生育阶段作物水分亏缺的概率分布状况,因此,该方法在分析农业干旱方面稍显不足。本文采用Archimedean Copula函数,结合干旱度指标对作物生育阶段降雨量进行分期划分,构建相邻生育阶段降雨量二维联合分布函数、分析研究该地区的作物生育阶段干旱特征,以期为区域干旱管理提供理论依据。
1 作物干旱指标与生育阶段降雨量
作物生育阶段水分的数学模型,包含供水时间和数量多少两方面对作物产量的影响,称为时间水分生产函数。该类模型将作物的连续生长过程划分为若干个不同生育阶段,认为在作物相同生育阶段水分具有同效性,在作物不同生育阶段才具有变化。M E Jensen(1968年)构建的Jensen模型给出了作物实际产量与作物相对蒸腾量之间的关系,而作物相对蒸腾量与生育阶段相对土壤水分胁迫之间存在某种联系。结合Jensen模型可定义出作物干旱度指标[16],见下式。
(1)
WCk=w0,k+Pk+Gk+Ik
(2)
WNk=wk+TEc,k
(3)
w0=1 000H1ηθ1
(4)
(5)
k=(1,2,…,t)
式中:Dr为评价区域干旱度,0≤Dr≤1,Dr=1为作物无收成,水分亏缺程度达到最大;Dr=0为作物丰收,水分不亏缺;λk为作物k阶段的敏感系数;WCk为作物第k阶段的供水量,mm;w0,k为作物第k阶段土壤初始贮水量供水量,mm;Pk为作物第k阶段时的有效降雨量,mm;Gk为作物第k阶段时的地下水补给量,mm;Ik为作物第k阶段时的净灌水量,mm;WNk为作物第k阶段的需水量,mm;TEc,k为作物第k阶段的蒸发蒸腾量,mm;wk为作物第k阶段正常生长发育所允许的最小土壤贮水量界限值,mm;Hk为作物第k阶段时的土壤计划湿润层深,m;θ1为作物第1阶段时的土壤含水率(以占土壤空隙体积的%计);t为作物生育阶段。
作物干旱度指标反映了区域在特定水文、气象、土壤及灌溉条件下由于缺水引起的作物减产情况。从以上公式可以看出,对于一个特定地区,作物敏感系数λk、需水量WNk是相对稳定的,作物干旱度指标主要与作物各阶段供水量有关。供水量WCk包括了4项内容,其中,对于北方地下水埋深较大的地区,Gk可忽略不计;w0,k主要由前期降雨量决定(w0,k-1主要受更前期的降雨量影响,TEc,k-1相对稳定,Gk-1忽略不计);阶段净灌水量Ik主要受人类活动影响,非自然因素;Pk为影响供水量的主要指标自然因素。通过上述分析可知,对于北方某一特定区域,在不考虑灌溉的情况下,各生育阶段降雨量为该区域干旱度的主要影响因素,如果能够对某种作物不同生育阶段降雨量及不同阶段之间的联系做一系统刻画,即可全面了解该区域的农业干旱状况,并针对旱情为不同阶段灌溉水量进行预估,从而为整个区域水资源调度提供依据。本文结合干旱度指标中的作物生育阶段划分,以实际调查为依据,统计某作物研究时段内各生育阶段降雨量,从而获取长系列以生育阶段为划分的降雨量序列。
2 基于生育阶段降雨量的两变量联合分布及检验
2.1 Copula函数概述
当选用相邻两个生育阶段降雨量来共同描述不同生育阶段干旱频率时,则需要度量两者之间的联系,即计算它们的联合概率分布函数。Copula理论已成为当今实现这种相关性分析的有效、通用的方法,其中Archimedean Copula函数因形式简单而被广泛应用,常用的Archimedean Copula函数有Gumbel-Hougaard、Frank和ClaytonCopula等十余种,表1列出了这几种常用Copula函数的表达式,θ为待定参数。

表1 4种常用的二维阿基米德Copula函数
2.2 各生育阶段降雨量单变量分布及检验
根据sklar定理,单变量概率分布即为多变量联合分布的边缘分布函数,合理确定单变量分布对最终确定的Copula函数的精确性有重要意义。大量数据分析计算表明,即使同为生育期降雨量,他们最佳分布函数类型也可能是不一致的,因此,对于不同的生育阶段,必须分别分析其分布函数。参考现有干旱水文干旱单变量分布研究成果,选定若干个备选分布函数,针对不同的分布函数对研究区各生育阶段降雨数据进行适线,然后根据经验点据与理论曲线的配合情况,选定各生育周期边缘分布类型。本文备选的单变量分布函数见表3。
对于某个生育阶段的降雨量,本文首先采用极大似然法(MLM)估计各备选分布函数的统计参数,然后进行分布函数的拟合度检验与评价,并最终选定该生育阶段降雨量的分布类型。具体检验评价步骤如下:①给定置信水平α,本文取90%;②利用传统的X2检验在给定置信水平条件下各备选分布函数是否通过检验;③若多个分布函数均通过检验,则进一步采用的是离差平方和最小准则(OLS)进行评价并最终选取该生育阶段降雨量的分布函数。OLS的计算公式为:
(6)
式中:Pi为理论频率;Pei为经验频率;n为样本容量。
采用该方法可确定各生育阶段降雨量的分布函数类型及其统计参数。
2.3 相依性度量
在用Copula函数描述变量间的相关性结构之前,还必须进行单变量相关性分析,以考察各变量之间的相关程度,确保它们是非独立的。相关系数是衡量随机变量之间相关性常用的指标,本文Spearman相关系数rn描述相邻生育阶段两两之间的相关关系:
(7)

本文采用t-检验检验两变量间的其相关性,当计算出的rn大于临界值rα时,则认为两个变量具有相关关系。
2.4 基于Copula函数的分布及检验
本文采用分步法计算Copula函数的统计参数,即当各生育期降雨量分布确定以后,再对相邻两个生育周期降雨量进行Copula拟合。对于某个选定的Copula函数,仍采用MLM法进行估计,求解方程组(8)即可得到Copula函数对应参数估计值。
(8)
式中:θ为参数集;αi为边缘分布函数参数;Fk为边缘分布函数;c(·)则为Copula函数的密度函数。
对于多个Copula函数,本文采用AIC信息准则法对其进行优越性评价。AIC信息准则包括两个部分:Copula函数拟合的偏差与Copula函数参数个数导致的不稳定性,AIC表达为:
(9)
AIC=nlnMSE+2m
(10)
(11)
式中:m为模型参数个数。
判断依据为,AIC数值越小则说明拟合度越好。
3 二维组合概率和重现期
为了更好的论述不同生育周期联合概率及其重现期,现对不同生育周期降雨量变量以JYLi(i=0,1,…,n)表示,i代表不同的生育阶段,0阶段为作物播种前的前期降雨阶段,n为某作物划分的生育阶段总数。各生育阶段对应的边缘分布记为ui(i=0,1,…,n)。作为二维分布函数,概率与重现期公式,关键取决于所选取变量的不同,本文以第一、第二生育阶段联合分布为例说明各个情况下的联合分布特性。本文选取如下3种概率/重现期从不同侧面对作物生育阶段干旱频率进行分析。
3.1 同现概率与同现重现期
同现概率与同现重现期刻画了连续两个生育阶段发生干旱状况的概率分布。
JYL1与JYL2同现不超越概率:
P(JYL1≤jyl1and JYL2≤jyl2)=C(u1,u2)
(12)
JYL1与JYL2不超越某个历时的同现重现期:
(13)
式中:E(L)and为JYL1与JYL2的同现历时,即连续两个JYL1≤jyl1and JYL2≤jyl2年份相距时长的数学期望,年。
3.2 联合概率与联合重现期
联合概率与联合重现期刻画了连续两个生育阶段最少一个阶段发生干旱的概率分布。
JYL1与JYL2联合不超越概率:
P(JYL1≤jyl1or JYL2≤jyl2)=u1+u2-C(u1,u2)
(14)
JYL1与JYL2不超越某个历时的联合重现期:
(15)
式中:E(L)or为JYL1与JYL2的联合历时,即连续两个JYL1≤jyl1or JYL2≤jyl2年份相距时长的数学期望,单位为年。
3.3 条件概率与重现期
条件概率与条件重现期刻画了连续两个生育阶段在第一个发生某种干旱状况的条件下第二生育阶段发生干旱的概率分布。
给定JYL1小于等于某定值条件下JYL2的条件概率:
(16)
(17)
式中:E(L)2|1为给定JYL1小于等于某定值条件下JYL2的联合历时,即JYL1小于等于某定值条件下,连续两个JYL2≤jyl2年份相距时长的数学期望,年。
4 应用实例
河南省渠村引黄灌区位于濮阳市西部,属东亚季风区,灌区内农作物种植面积为22.91 万hm2,主要作物为小麦、玉米和棉花,现有该灌区1961-2013共53 a逐月降雨资料。该地区玉米生育周期为[17]:第一阶段,播种~苗期(06-05-06-25),降雨量记为jyl1;第二阶段,拔节~抽穗(06-25-07-11)降雨量记为jyl2;第三阶段,抽穗~乳熟(07-12-08-12) 降雨量记为jyl3;第四阶段,乳熟~收获(08-13-09-02),降雨量记为jyl4;以播种前15 d(05-20-06-05)作为播种前期以充分考虑前期降雨对土壤含水量的影响,降雨量记为jyl0。本文以濮阳渠村灌区玉米种植为例对Copula函数在农业干旱分析中的应用加以说明。根据上述生育阶段的划分,渠村灌区玉米不同生育阶段降雨量统计特征值见表2。
4.1 边缘分布的确定
针对不同的生育阶段,参考水文统计常用的分布函数,利用3.2节所介绍方法进行单变量拟合检验。各生育阶段参数估计见表3。
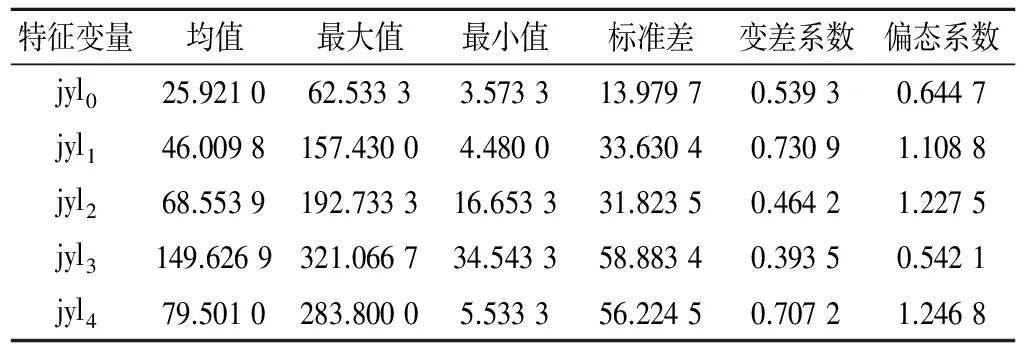
表2 各生育阶段降雨量统计特征表

表3 各生育阶段单变量参数估计成果表
X2检验结果为0表明通过检验,OLS越小,说明拟合度越好。从表3可以看出,jyl0服从gamma分布,jyl1、jyl2服从Lognormal分布,jyl3、jyl4服从Weibull分布。
4.2 相邻生育阶段降雨量相依性度量
利用3.3节所介绍方法进行变量相关性检验,检验结果见表4。

表4 相邻生育阶段降雨量相关系系数计算成果表
对相关系数进行显著性检验,对于样本容量n=53,置信水平α取90%时,临界相关系数rα为0.2306,从表4可以看出,相邻生育阶段降雨量之间的相关系数均大于临界相关系数,存在显著的相关性。
4.3 联合分布的确定
针对2.1节所描述的几种Archimedean Copula函数,利用3.4节所述方法对相邻两个生育阶段降雨量进行拟合并进行测评,其结果见表5。

表5 相邻生育阶段Copula函数参数估计与拟合度评价
表5中,“-”表示统计参数超出了定义域范围,不参与测评。从表5可看出,相邻两个生育阶段降雨量均以Gumbel-Houggard Copula为最佳拟合。
4.4 相邻生育阶段降雨量组合概率与重现期分析
根据4.2节确定的Gumbel-Houggard Copula函数参数,利用第3节所述方法计算相邻生育阶段降雨量的同现概率、联合概率及条件概率,见图1~图3。并可计算出其相应的同现重现期、联合重现期及条件重现期,由于篇幅有限,本文仅列出jyl0、jyl1两个生育阶段对应的成果,见表6~表8,表中“-”为实测数据区,实际应用中若数据落在该区间,则通过插值求得。

图1 同现概率等值线图(单位:%)

图2 联合概率等值线图(单位:%)

图3 条件概率等值线图(单位:%)

表6 jyl0~ jyl1同现重现期计算成果表 年

表7 jyl0~ jyl1联合重现期计算成果表 年

表8 jyl0~ jyl1条件重现期计算成果表 年
首先,图1~图3、表6~表8以玉米生长过程为例系统反应区域农业干旱状况,便于对相邻两个区域农业干旱状况进行对比。
其次,可对研究区域某一具体年份的当前农业干旱状况做出评价,并为下阶段灌溉制度提供依据。例如,假定该区域阶段降雨量小于阶段平均值即会对该阶段作物生长产生干旱影响(表2可查出该区域阶段降雨量平均值),则从图1~图3可以查出P(JYL0≤25.92 and JYL1≤46.01)约为25%,P(JYL0≤25.92 and JYL1≤46.01)约为65%,P(JYL0≤25.92 and JYL1≤46.01)约为70%;从表6~表8可以查出相应的同现重现期为9年一遇,联合重现期为2年一遇,条件重现期为4年一遇。这表明该区域玉米生长的前两个生育阶段均发生干旱的概率不是很大(25%),但这两个生育阶段中至少一个阶段发生干旱的概率较大(65%),因此,前两个生育阶段应做抗旱准备;尤其地,根据条件概率,若第一阶段发生干旱,则第二阶段发生干旱的概率达70%,即,若第一阶段干旱,则有必要加强第二阶段的抗旱工作,从而为灌区水资源配置提供预估。
5 结 语
本文以濮阳渠村灌区玉米种植为例,对作物生育阶段降雨量进行分期划分。首先,拟合各生育阶段降雨量分布函数,然后,选用Archimedean Copula函数构造相邻生育阶段降雨量的联合分布,计算出相邻生育周期降雨量的组合概率与组合重现期。该方法分析了相邻生育阶段降雨量之间的多种组合情况,能够全面地反映区域作物生育阶段干旱的特征,可为区域内农业干旱分析和水资源配置提供指导。
[1] 于 艺,宋松柏,马明卫,等.Archimedean 族 Copulas 函数在多变量干旱特征分析中的应用[J].水文,2011,31(2):6-10.
[2] 孙可可,陈 进,金菊良,等.实际抗旱能力下的南方农业旱灾损失风险曲线计算方法[J].水利学报,2014,45(7):809-814.
[3] 唐 蕴,王 浩,严登华,等.嫩江流域近45年来径流演变规律研究[J].地理科学,2009,29(6):864-868.
[4] 金菊良,刘 丽,汪明武,等.基于三角模糊数随机模拟的地下水环境系统综合风险评价模型[J].地理科学,2011,31(2): 143-147.
[5] 闫宝伟,郭生练,陈 璐,等.长江和清江洪水遭遇风险分析[J].水利学报,2010,41(5) : 553-559.
[6] 冯 平,毛慧慧,王 勇.多变量情况下的水文频率分析方法及其应用[J].水利学报,2009,40(1) :33-37.
[7] 刘曾美,陈子桑.区间暴雨和外江洪水位遭遇组合的风险[J].水科学进展,2009,20(5):619-625.
[8] Genest C,Favre A C. Everything you always wanted to know about copula modeling but were afraid to ask [J].Journal of Hydrologic Engineering,2007,12(4):347-367.
[9] 周玉良,袁潇晨,金菊良,等.基于Copula的区域水文干旱频率分析[J]. 地理科学,2011,31(11):1 383-1 388.
[10] 陆桂华,闫桂霞,吴志勇,等.基于copula 函数的区域干旱分析方法[J].水科学进展,2010,2121(2):188-193.
[11] 徐春晓,袁潇晨,金菊良,等.基于Copula的区域干旱空间分布特征分析[J].资源科学,2011,33(12):2 301-2 313.
[12] Shiau J T.Fitting drought duration and severity with two-dimensional Copulas[J].Water Resources Management,2006,20(5):795-815.
[13] 宋松柏,蔡焕杰,金菊良,等.Copulas函数及其在水文中的应用[M].北京:科学出版社,2012.
[14] 陈永勤,孙 鹏,张 强,等.基于Copula的鄱阳湖流域水文干旱频率分析[J].自然灾害学报,2013,22(1):75-84.
[15] 李 计,李 毅,贺缠生.基于Copula函数的黑河流域干旱频率分析[J].西北农林科技大学学报(自然科学版),2013,41(1) :213-220.
[16] 陈海涛,黄 鑫,邱 林,等.基于最大熵原理的区域农业干旱度概率分布模型[J].水利学报,2013,44(2):221-226.
[17] 陈晓楠,段春青,刘昌明,等.基于两层土壤计算模式的农业干旱风险评估模型[J].农业工程学报,2009,25(9):51-55.
