热噪声试验温度场分析方法研究

刘宝瑞，李海波，贾洲侠，吴振强，程 昊



热噪声试验温度场分析方法研究

刘宝瑞，李海波，贾洲侠，吴振强，程 昊

（北京强度环境研究所，可靠性与环境工程技术重点实验室，北京，100076）

针对热噪声试验系统设计与评估需求，建立了热噪声试验系统热分析计算模型，采用宏观流团与流动路径建立噪声气流换热模型，基于蒙特卡罗法计算辐射换热，基于热网络法获得不同加热功率下主要受热部件的温度场分布规律。通过和热噪声试验结果的对比分析，验证了计算模型的有效性，并在此基础上对热噪声试验系统在噪声环境下的最大加热能力进行了预测，为热噪声试验系统的性能评估和设计优化提供了技术支撑。

热噪声试验系统；热网络法；蒙特卡罗法；温度场

0 引 言

飞行器在大气层中高超声速巡航或者再入飞行时，飞行器结构表面将承受严酷的气动热环境和高量级噪声环境。大面积防热结构的温度超过1200 ℃，鼻锥、翼前缘等区域温度超过2000 ℃，结构在高温环境下的材料力学性能、动力学特性等会发生改变，影响飞行器结构承载能力和飞行控制[1]。开展热噪声试验、考核结构在热噪声环境中的完整性和耐久性是高超声速飞行器结构设计必须开展的工作[2~7]。热噪声试验面临高量级噪声载荷和大热流热载荷同时施加的问题，既要满足试验件表面的噪声量级和温度条件，又要保证试验系统在高温环境下可靠工作，准确的热噪声试验系统温度场分析是其中加热系统设计的关键。

本文研究的热噪声试验系统采用石英灯辐射加热装置施加热载荷，采用液氮供气系统、行波管和电动扬声器模拟噪声载荷。试验过程中，低温高速的噪声气流在通过行波管试验段时对试验件有强烈的冷却作用，石英灯加热器到试验件之间有行波管、热防护挡板和石英窗等部件，试验系统热交换关系十分复杂，辐射、导热、自然/强迫对流等多种换热形式同时作用。目前还未有文献针对热噪声试验系统温度场进行建模计算，试验系统设计缺乏科学方法，往往只能通过经验进行估算。采用CFD方法能够较准确地模拟对流换热效应，但是辐射换热模拟精度较差，而且计算效率较低；采用商用有限元软件计算效率较高，但是噪声气流的对流换热计算过于简化，且辐射换热计算精度较差。

本文采用Sinda/Fluint软件建立了热噪声试验的热分析计算模型，采用宏观流团建模方法模拟噪声气流的强迫对流换热，基于蒙特卡罗法计算辐射换热，基于热网络法获得不同加热功率下主要受热部件的温度场分布规律。通过和试验结果的对比分析验证了计算模型的准确性，并在此基础上对热噪声试验系统在热噪声复合载荷作用下的最大加热能力进行了预测。

1 研究模型

本文针对文献[1]所描述的热噪声试验系统开展温度场计算分析，试验系统如图1所示。试验件固定于行波管侧壁，加热器为带反射板的石英灯组，石英灯组透过固定在行波管一侧的石英窗对另一侧的试验件进行加热，行波管内通有噪声气流。

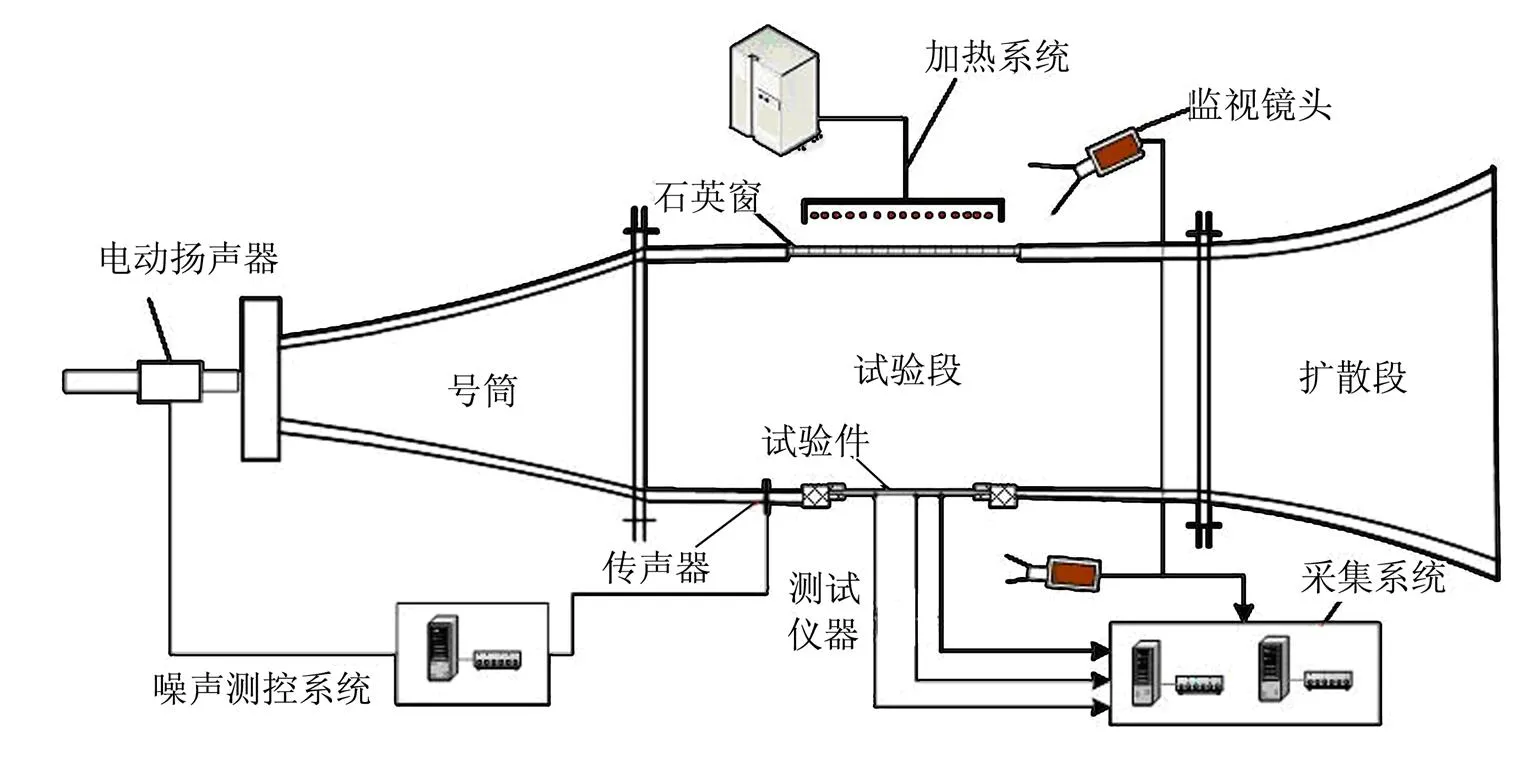
图1 热噪声试验系统

截取热噪声试验系统试验段，基于Sinda/Fluint软件建立热分析计算模型如图2所示，包括石英灯加热器、行波管、石英窗和试验件等主要部件。

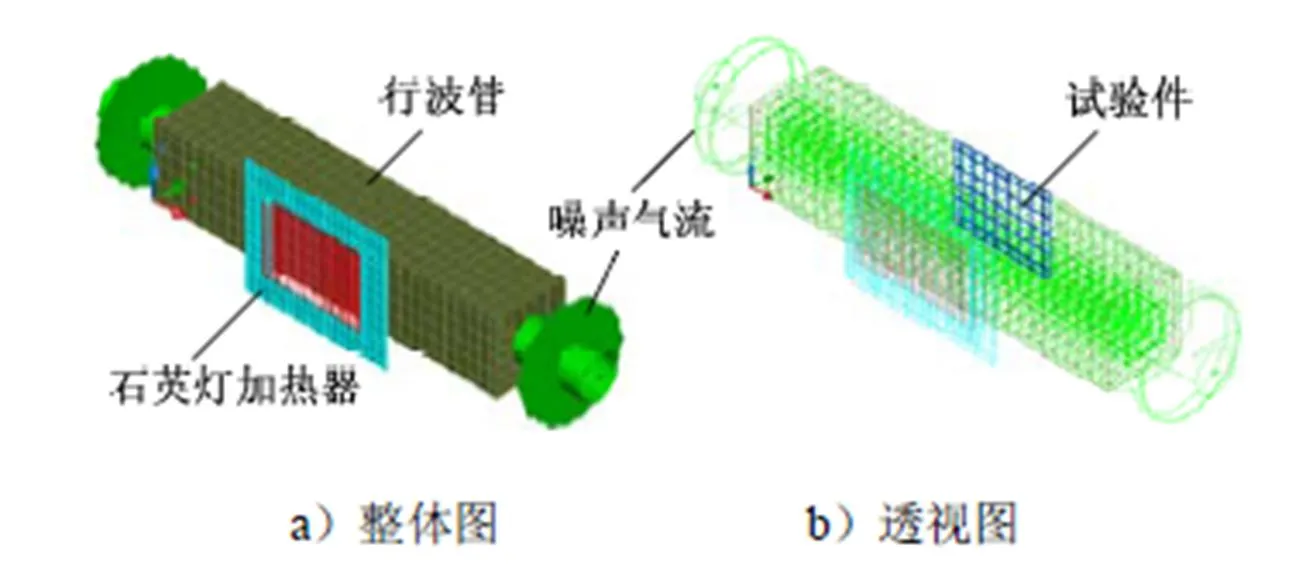
图2 试验段热分析模型

行波管试验段为壁厚8 mm的不锈钢方形管状结构，侧壁有两个长方形孔安装试验件和石英窗，考虑到不锈钢的导热性能较好，温度沿管壁厚度方向变化不大，因此忽略管壁厚度方向的温度差异，用面单元模拟行波管管壁。试验件为2 mm厚钛合金平板，通过螺栓固定于行波管侧壁，忽略对温度场影响不大的螺栓孔的建模和厚度方向的温度差异，采用矩形面单元模拟试验件。加热装置为带反射板的石英灯加热器，灯丝为螺旋缠绕形状的钨丝，采用圆柱面单元建模并施加表面热载荷，反射板以矩形面单元模拟，并设置为恒温边界条件。

外部空气与各个部件之间存在自然对流换热关系，根据各壁面的位置分布分别采用空气与水平板和空气与竖直壁板的自然对流换热模型进行计算。

采用热网络法建立行波管内噪声气流的传热模型，如图3所示。

图3 噪声气流传热模型

将行波管内的噪声气流沿流动方向划分为若干个流团，假设整个温度场分析过程中每个流团内部温度均匀，初始条件设置为常温、常压条件。在行波管试验段上游建立流入边界流团，根据所用的氮气源设置温度和压力边界条件。在行波管试验段下游建立流出边界流团，设置为常温、常压边界条件。行波管试验段内各相邻流团间沿气流流动方向建立流动路径，连接相邻流团，传递各流团间的温度、压力信息。每个流团的温度、压力和流量的关系采用如下方程计算：

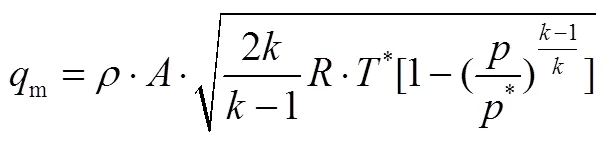
式中m为行波管内气体质量流量；为流团气体密度；为流团所在位置行波管横截面积；为气体常数；为气体比热比；*为气体总温；*为气体总压；为气体静压。

行波管内气体流量根据如下方程计算：

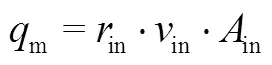
式中in为进口气体流速；in为流道横截面积，其中根据文献[4]所描述的噪声声压级与噪声气流速度关系确定。

在流入边界流团和行波管试验段首个流团间沿流动方向建立流入流动路径，设置流动横截面积、体积流量、质量流量等流入流动路径参数。

在行波管试验段末个流团和流出边界流团间沿流动方向建立流出流动路径，设置流动横截面积、质量流量、流阻系数等流出流动路径参数，压力损失Δout按照如下方程计算：

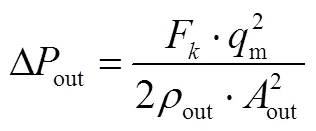
式中F为出口流阻系数，根据行波管出口形状计算；out为出口气体密度；out为出口流道横截面积。

建立流团与行波管壁对流换热模型，采用流体在方形管路内流动时的强迫对流换热模型计算对流换热系数，行波管试验段流团簇和行波管内壁面间的强迫对流换热系数采用如下方程计算[8]：

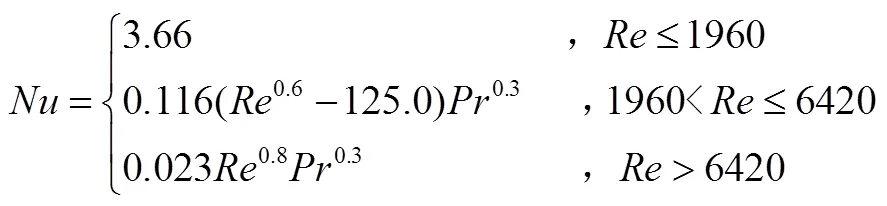
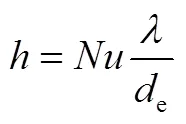
式中为努赛尔数；为噪声气流雷诺数，时为层流区，时为过渡区，时为湍流区；为噪声气流普朗特数；为噪声气流导热系数；e为行波管横截面的当量直径。

2 计算方法

基于热网络法，对结构件的温度场和其周边的流场进行同步求解[9,10]。对于结构中任意一个温度节点，以稳态传热为例，达到热平衡时，节点的静热流量为零，假设结构总共有个节点，其中第个节点上的热平衡方程可表示为

式中Q为节点自身产生的热量以及通过辐射方式传入的热量；f为节点和相邻节点之间的传热关系；对于对流换热传热，f=()，其中：为两个节点和之间的对流换热系数，为换热面积，对于导热传热，f=(/)；为导热系数；为节点距离；T，T分别为节点和的温度。

针对每个节点建立热平衡方程，可以得到整体结构的热平衡方程组，即：

对于温度已知的热边界节点，采用热边界方程：

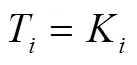
其中，K表示边界节点的温度值，进一步获得如下热平衡方程组：

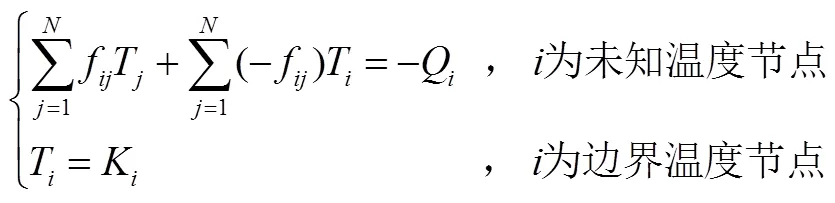
求解式（9）即可得到各未知节点的温度值。

采用蒙特卡罗方法计算各节点的辐射热流。蒙特卡罗方法是以概率统计理论为基础的一种方法，在求解辐射热流密度方面具有较高的计算效率[11]。求解辐射热流密度的基本思想是：令每个石英灯丝温度节点发射大量独立能束，通过随机数描述能束的发射位置和发射方向，将辐射传输过程的发射、透射、反射、吸收和散射等过程转化为随机问题，建立每个过程的概率模型，通过几何空间分析对各能束的归宿进行跟踪，判断能束节点吸收、透射或逸出等情况，进一步通过统计处理得到辐射热流场分布。以石英灯辐射加热系统为例，其辐射传热物理模型如图4所示。灯丝的辐射能首先与灯管相互作用，在灯管内外壁面经历吸收、折射、反射、透射等过程，从石英灯管透射出的能量入射到反射板及目标面上或逸出系统，其中入射到反射板的能量一部分被吸收、一部分被反射到其他目标面或逸出系统，被目标面或逸出的能束则结束历程。对以上能束最终归宿进行统计处理，即可获得系统各节点的辐射热流密度，即式（7）中的Q。

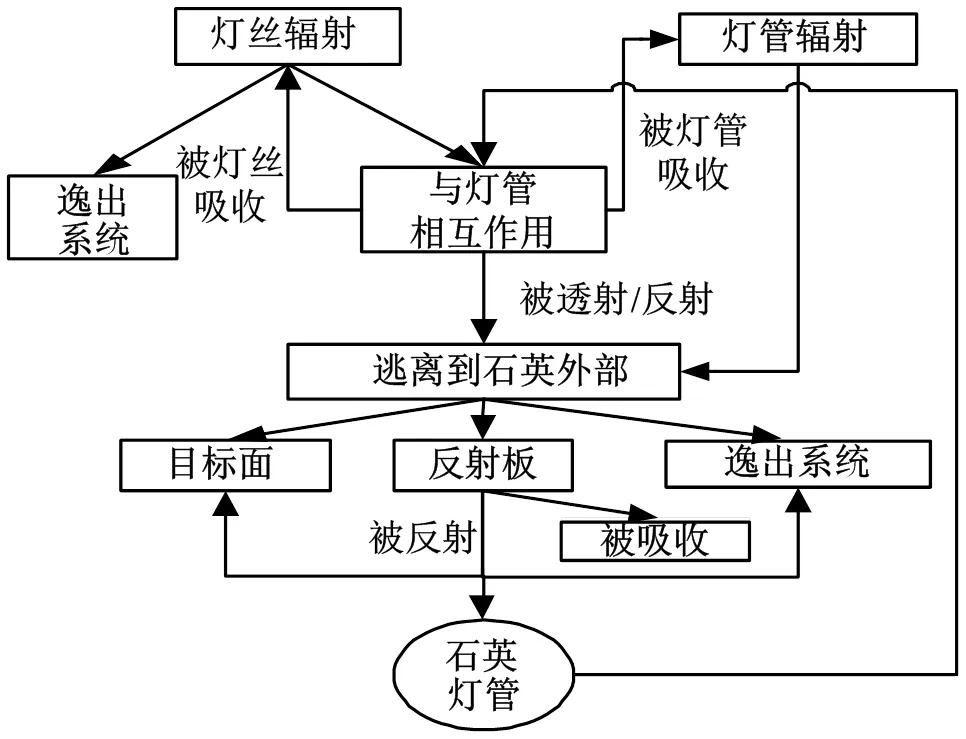
图4 石英灯加热系统能束的物理过程

3 计算结果与分析

3.1 单一热环境热分析计算

针对单一热环境试验工况，采用如图5所示的石英灯加热功率曲线进行瞬态热分析计算，得到主要受热部件的温度场分布随加热时间的变化规律。

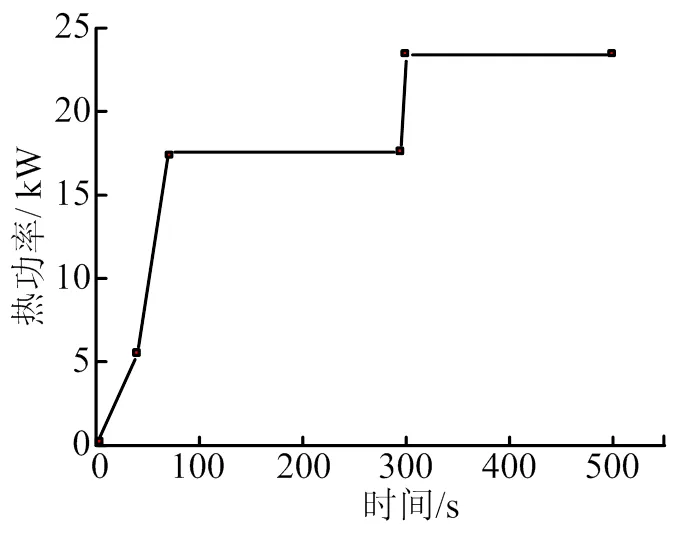
图5 石英灯组加热功率随时间变化

图6为计算得到的试验件400 s时的温度场分布图。从图6中可以看出，试验件的温度场分布并不均匀，中心温度最高，呈辐射状向四周逐渐降低，最高温度约为533 ℃。

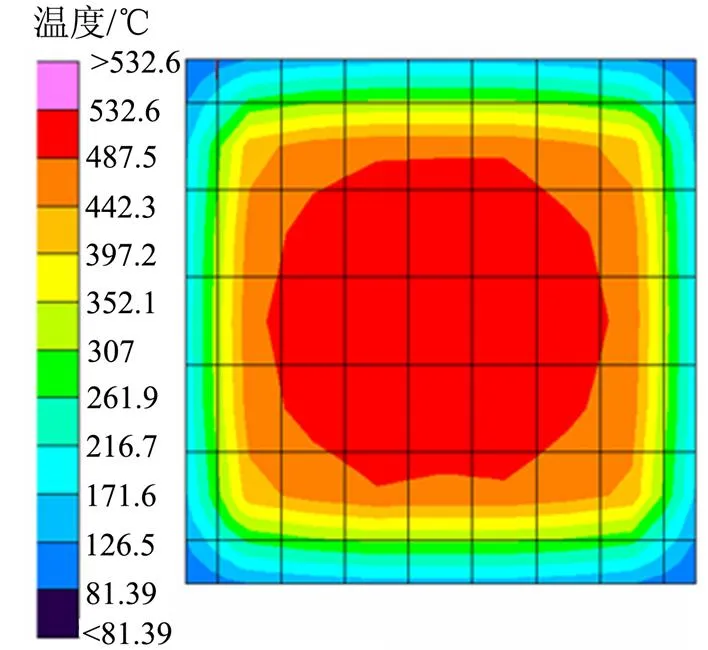
图6 单一热环境试验件温度场分布图（400s）

图7为行波管温度场分布图，最高温度出现在中间段靠近石英灯组加热器的一端，约为192 ℃。

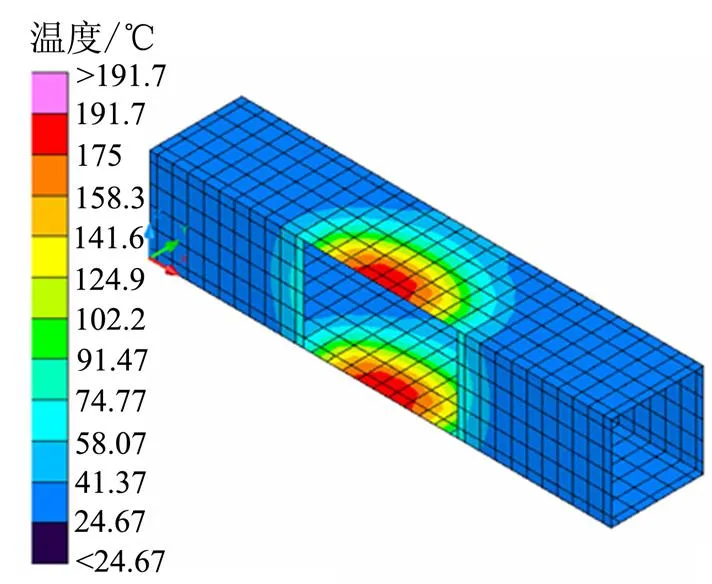
图7 单一热环境行波管温度场分布图（400s）

图8为试验件温度测点试验结果和计算结果随时间的变化曲线。

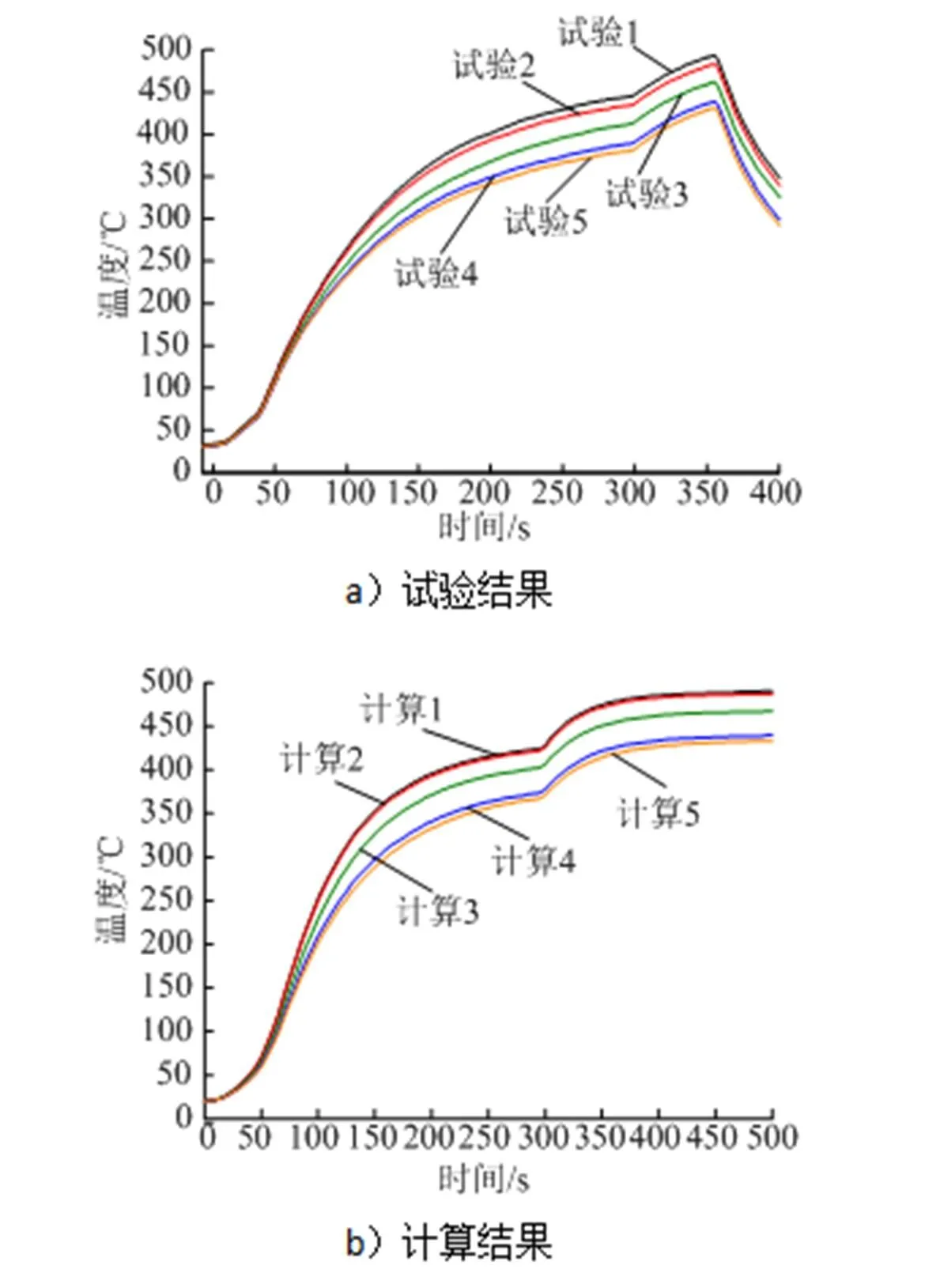
图8 单一热环境下试验件温度测点随时间变化曲线

由图8可以看出，试验件温度的计算结果和试验结果变化趋势一致，试验件温度随着石英灯组加热功率的增加而增加，在70～300 s时加热功率保持17.57 kW恒定，试验件温度逐步达到稳态；将功率继续加大到 23.4 kW，约450 s以后试验件温度场达到稳态，测点最高温度约为490 ℃。通过对比发现，350 s之前，试验件测点位置计算结果和试验结果的变化规律和数值的一致性较好，验证了方法的可行性。试验在360 s之后进行了卸载，温度出现下降。

3.2 热噪声复合环境热分析计算

在单一热环境瞬态热分析模型的基础上，建立噪声气流与热噪声试验系统的换热分析模型，进行了热噪声复合环境下的瞬态热分析计算。按图5所示曲线改变石英灯组的加载功率，得到热噪声试验装置的瞬态温度场分布，如图9~11所示，热噪声复合环境下试验件和行波管的温度场分布规律和单一热环境下基本一致，由于噪声气流对行波管和试验件的强迫对流冷却作用，最高加热温度下降至约470 ℃，温度下降63 ℃，且达到热平衡的时间提前约50 s。文献[4]开展了热噪声复合环境试验，首先将试验件加热到500 ℃，然后施加150 dB噪声载荷，噪声气流使得试验件温度下降50~100 ℃，验证了本文热噪声复合环境热分析计算方法的有效性。

图9 热噪声复合环境下试验件温度场分布图（400s）

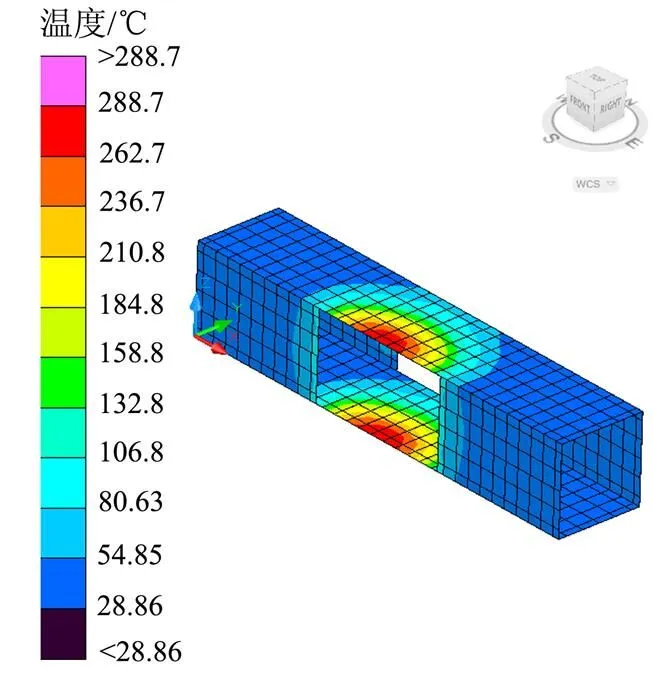
图10 热噪声复合环境下行波管温度场（400s）

图11 热噪声复合环境下试验件温度测点随时间变化曲线

3.3 热噪声复合环境下试验系统的加热能力预测

采用以上热分析模型对该热噪声试验系统设计方案在噪声工况下的加热能力进行预测，获得热噪声复合环境下试验件中心点温度随石英灯组加热功率的变化规律如图12所示，由图12中可以看出，试验件温度随着石英灯组加热功率的增大而增大，但增大的幅度逐渐减小，在石英灯组功率66 kW情况下，试验件中心温度最高为709 ℃，行波管的最高温度为638 ℃。为了保护试验装置不受损坏和试验安全，需要对行波管进行适当热防护。

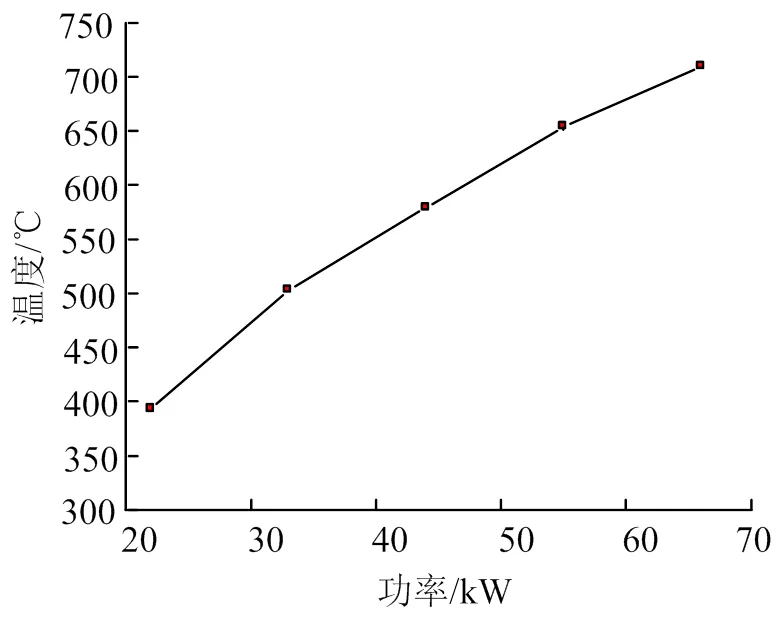
图12 试验件中心温度随石英灯组加热功率的变化曲线

4 结束语

本文建立了某热噪声试验装置的热分析计算模型，综合考虑辐射、自然/强迫对流、导热等多种换热形式，采用宏观流团建模方法模拟噪声气流的强迫对流换热，基于蒙特卡罗法计算辐射换热，基于热网络法获得不同加热功率下主要受热部件的温度场分布规律，计算结果和试验数据取得了良好的一致性。进一步对该热噪声试验系统的加热能力进行预测，得到了试验件温度随加热功率的变化规律以及最大加热能力，能够为热噪声试验系统设计提供技术支撑。

[1] 吴振强, 李海波, 程昊, 等. 热环境下金属壁板噪声激励动响应试验研究[J]. 强度与环境, 2016, 43(2): 25-33.

Wu Zhenqiang, Li Haibo, Cheng Hao, et al. Dynamic response tests of metallic panels excited by acoustic loads in thermal environment[J]. Structrure & Environment Engineering, 2016, 43(2): 25-33.

[2] 蒋持平, 柴慧, 严鹏. 近空间高超声速飞行器防热隔热与热力耦合研究进展[J]. 力学与实践, 2011, 33(1): 1-9.

Jiang Chiping, Chai Hui, Yan Peng. Advances in thermal protection of near space hypersonic flying vehicles and related researches of thermal-mechanical coupling[J]. Mechanics in Engineering, 2011, 33(1): 1-9.

[3] 吴振强, 任方, 张伟, 等. 飞行器结构热噪声试验的研究进展[J]. 导弹与航天运载技术, 2010 (2): 24-30.

Wu Zhengqiang, Ren Fang, Zhang Wei, et al. Advances in thermal-acoustic testing of aerospace structures[J]. Missiles and Space Vehicles, 2010 (2): 24-30.

[4] 吴振强, 张伟, 孔凡金, 等. 热噪声复合环境试验装置研制及其能力验证[J]. 导弹与航天运载技术, 2014(5): 60-67.

Wu Zhengqiang, Ren Fang, Zhang Wei, et al. Research and capability verification of the test apparatus simulating combined thermal and acoustic environment[J]. Missiles and Space Vehicles, 2014(5): 60-67.

[5] Swanson A D, Coghlan S C, Pratt D M, et al. Hypersonic vehicle thermal test challenges[R]. AIAA-2007-1670, 2007.

[6] Clarkson B L. Review of sonic fatigue technology[R]. NASA-N94-29407, 1994.

[7] Mixson J S, Roussos L A. Acoustic fatigue: overview of activities at NASA Langley[R]. NASA-N87-24965, 1987.

[8] 杨世铭, 陶文铨. 传热学[M]. 北京: 高等教育出版社, 2006.

Yang Shiming, Tao Wenquan. Heat trasfer theory[M]. Beijing: Higher Education Press, 2006.

[9] Cullimore B A, Ring S G, et al. SINDA/FLUINT user’s manual[M]. Colorado: C&R Technologies, Inc. 2010.

[10] Panczak T D, Ring S G, et al. Thermal desktop user’s manual[M]. Colorado: C&R Technologies, Inc. 2010.

[11] 刘宝瑞, 孔凡金, 张伟, 等. C/SiC舵结构热试验瞬态温度场预示技 术[J]. 强度与环境, 2015, 42(1): 40-45.

Liu Baorui, Kong Fanjin, Zhang Wei, et al. Prediction techniques of transient temperature distribution during thermal tests for C/SiC rudder[J]. Structure & Environment Engineering, 2015, 42(1): 40-45.

Study on the Temperature Distribution Analysis Method of the Thermal-acoustic Experiment

Liu Bao-rui, Li Hai-bo, Jia Zhou-xia, Wu Zhen-qiang, Cheng Hao

(Science and Technology on Reliability and Environment Engineering Laboratory, Beijing Institute of Structure and Environment Engineering, Beijing, 100076)

For the design and evaluation of the thermal-acoustic experimental system, the thermal model of the thermal-acoustic experimental system is built. The acoustic flow model is built by lumps and tubes. The radiation heat rate is calculated by Monte-Carlo theory. The steady and the transient state temperature distributions of the main components are obtained based on the thermal network theory. The validity of the model is proved by comparing with the test results, and the maximal heating ability of the thermal-acoustic experimental system is predicted, which can be used to support the performance evaluation and the design optimization of the system.

Thermal-acoustic experimental system; Thermal network theory; Monte-arlo theory; Temperature distribution

1004-7182(2018)01-0116-06

10.7654/j.issn.1004-7182.20180123

V216.5

A

2016-11-28；

2017-01-21

刘宝瑞（1985-），男，高级工程师，主要研究方向为结构力热试验与分析技术