液体重定位推力时序的优化研究

刘 桢，王丽霞，林 宏，林 若，周运强



液体重定位推力时序的优化研究

刘 桢1，王丽霞2，林 宏3，林 若1，周运强1

（1. 北京航天长征飞行器研究所，北京，100076；2. 北京强度环境研究所，北京，100076；3. 北京宇航系统工程研究所，北京，100076）

研究了液体重定位的数值仿真方法，并利用半人马座在美国路易斯落塔试验室的落塔试验结果验证该计算方法的准确性，使用该数值仿真的方法对某贮箱液体重定位推力时序进行优化研究，研究结果表明通过对推力时序的优化能够加速液体重定位并能有效减少该过程需要消耗的能量。

微重力液体管理；液体重定位；推力时序优化

0 引 言

飞行器在轨无动力滑行时，贮箱内的液体推进剂处于微重力环境而悬浮于贮箱中的任意位置。若飞行器是在低轨滑行，稀薄空气的阻力作用甚至会使贮箱内的液体推进剂移动到贮箱的上底处。此时，飞行器要完成变轨、轨道调整或位置保持等动作，必须在主发动机启动前使用姿控发动机推力将悬浮的液体推进剂重新定位到贮箱下底的出口处。液体的这个流动过程称之为重定位过程，而利用这种方法实现在轨滑行飞行器多次启动的液体管理方法就是正推重定位管理方式[1]。

正推重定位管理方式中由于贮箱里没有设置额外的推进剂管理装置（Propellant Management Devices，PMD），因此不存在推进剂与结构材料之间的兼容性问题，经常应用于长时间滑行的低温上面级液体管理，例如，美国通用上面级——半人马座系列[2]等。

在正推重定位推力时序设计时，总是希望尽量通过合理控制液体的惯性力，来抑制重定位过程中的液体动能并加速其衰减，达到贮箱内液体快速稳定的目的。20世纪80年代末，美国提出脉冲式重定位的方 法[3,4]，通过合理地对推力大小、推力作用时间和周期进行优化，减少了姿控系统推进剂消耗量、提高有效运载能力。

在地基上开展液体重定位试验研究需要建造很高的落塔设备来提供足够的失重时间，研究周期很长且成本高。而基于天基（如空间站等）的试验研究在试验准备和试验操作上尚存在很多难以解决的问题。本文旨在对贮箱内液体重定位过程采用有限体积数值仿真的方法来研究液体重定位过程推力时序设计的有效优化。

1 重定位过程和数值仿真

液体重定位问题是一种无法用数学公式描述的复杂气、液两相流问题，要准确地对贮箱内液体重定位过程进行数值仿真，必须先要了解重定位过程各阶段的物理特征。

重定位过程中的姿控推力一般比较小，属于低重力的过载环境范畴，此时，表面张力对流动作用还不能忽略。因此，液体重定位流动的控制力主要包括姿控推力产生的惯性力、液体的黏性力和流动相的表面张力等。

从流动特征来看重定位过程可分为4个阶段[5]（见图1）：a）液体呈薄层状从箱顶沿箱壁向箱底加速流动过程；b）薄层状流动液体前沿在箱底汇合以“喷泉”状涌起；c）“喷泉”消失，所有液体在箱底聚集晃动；d）箱内液体基本平稳，液体中混夹的气泡逐渐上升析出。

图1 重定位过程

数值计算的初始状态，需先构造尽量与实际状态一致的流体区域，然后以某一特定条件（如“邦德数=15[6]”等）维持贮箱内液面的低重形状达到平衡，以保证重定位开始时所有液体沿箱壁向下流动。由重定位过程特征可知，该问题是一个典型的气、液两相流问题，重定位流动开始之后，在整个重定位流动过程中箱内气枕不仅影响着前期薄层的流动形态，在中期气枕分裂成气泡、气泡破碎成小气泡以及后期的小气泡合并成大气泡析出都是液体重定位过程重要的组成部分。

因此，在数值计算过程中不能简单地只考虑表面张力和贮箱整体的气液界面，可以采用绝热气泡模型模拟流动过程中气体内压力、位置的变化导致气泡的体积变化以及分裂、合并析出等现象。重定位过程中液体流速比较低，此时，可以忽略液体的湍流效应而采用层流模型来考虑液体黏性力对运动的影响。

2 人马座落塔试验和数值仿真的验证

人马座重定位落塔试验研究[6]是在美国路易斯（Lewis）零重力设备上完成的，该落塔设备的自由落体高度约为142 m，可以提供大约5 s的失重时间。此零重力设备的自由落体高度处于世界领先水平，即便如此，其所能提供的失重时间与实际的人马座贮箱重定位的时间还是不在一个量级，而必须采用缩比模型进行模拟试验，通过牺牲模型的几何尺度来延长模拟试验的时间尺度。试验中用于模拟氧化剂箱和燃烧剂箱的模型贮箱半径为5.5 cm和7.0 cm，长度分别为 21.8 cm和27.8 cm，分别以Freon-TF和FC-78为试验液体，并通过反推喷气系统调节下落时的推力来达到重定位初期以及重定位流动开始之后的邦德数相似。

图2为人马座落塔试验和数值仿真对比。图2a是半径为7.0 cm，长度为27.8 cm的人马座缩比贮箱重定位试验结果。人马座落塔试验初期使用邦德数=15维持贮箱内液面的低重形状。试验中典型重定位过程的前2个阶段的特征非常明显，由于邦德数较大，流体的惯性作用影响显著，薄层状流动液体前沿在箱底汇合后涌起强健有力的柱状“喷泉”，喷泉冲上贮箱的顶部后再沿箱壁往下流动形成流动循环。试验后期流体动能减少逐渐使喷泉变细，最后消失。由于落塔时间的限制，重定位的过程中喷泉消失后的晃动以及液面基本平稳之后的气泡析出过程无法通过试验模拟。图2b是采用有限体积的数值计算方法对人马座缩比贮箱重定位试验进行数值仿真得到的在相同特征时刻的流型图。

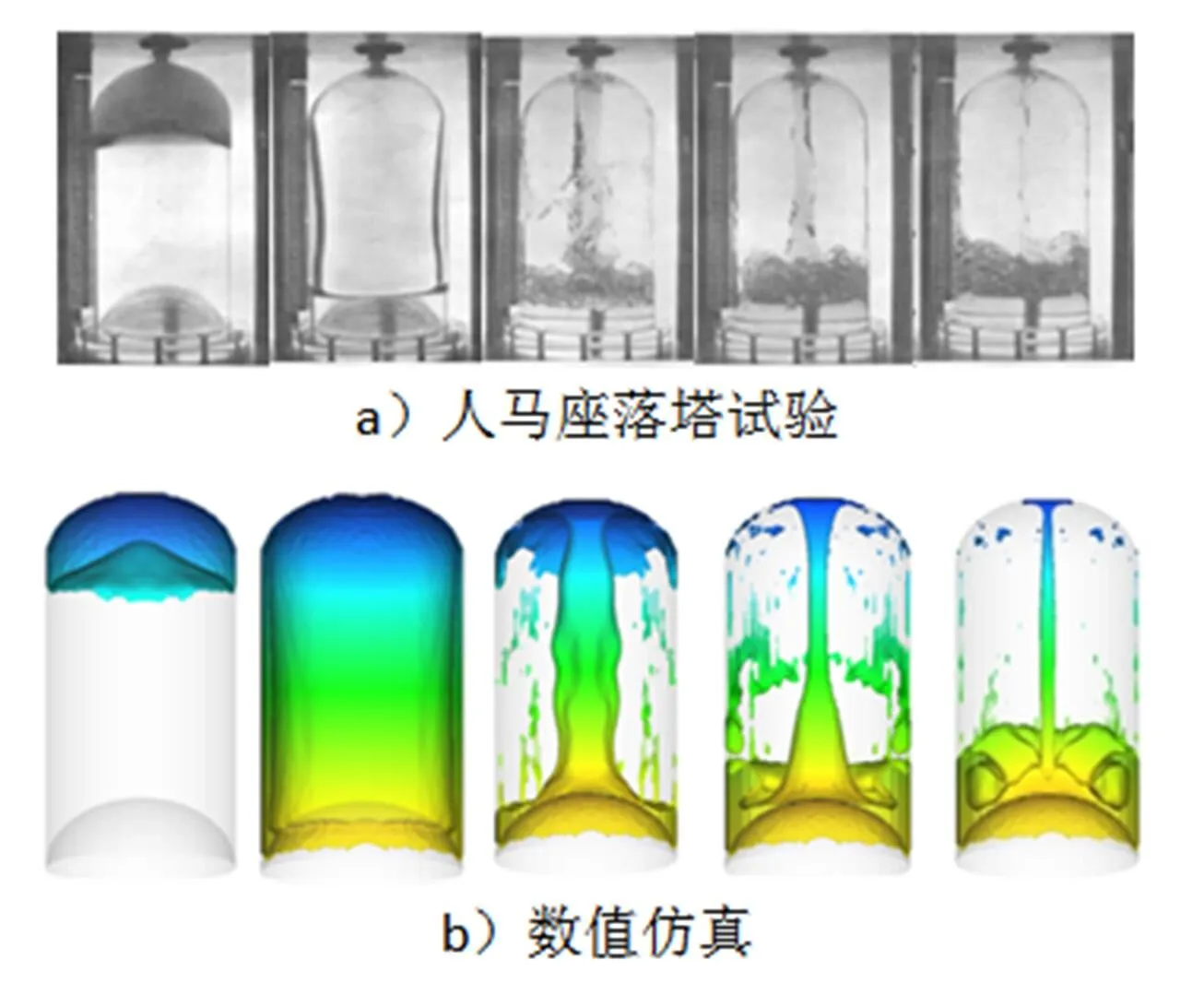
图2 人马座落塔试验和数值仿真对比

从图2中可以看出，数值仿真的液体重定位过程与试验研究过程一致性很好，在同一特征时刻，数值仿真的液体的运动形态与试验结果非常一致。从而说明数值计算中采用的物理模型基本上符合液体重定位过程的物理特征。由于数值计算相比于试验研究方法来说具有不受自由落体时间限制的优势，非常适用于液体重定位推力时序设计的优化。

3 重定位推力时序优化研究

在现役飞行器的实际应用中，通常采用小推力发动机推力让液体沉底来减少液体在重定位过程对贮箱的反向冲击，同时达到减少姿控系统燃料消耗的目的，等液体基本聚集在箱底后再采用大推力发动机推力抑制贮箱内液体晃动，加速气泡析出，确保能给主发动机启动输送不夹气的推进剂。典型液体重定位推力时序如图3所示[1]。

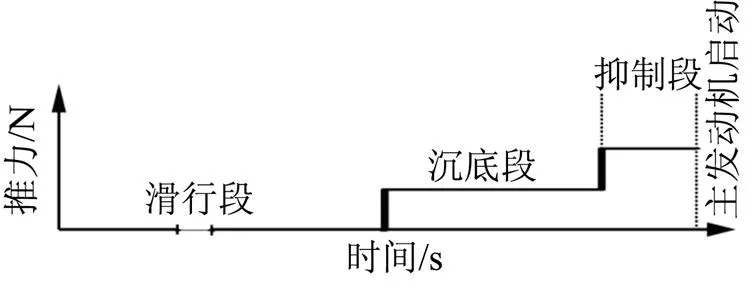
图3 液体重定位典型推力时序

沉底段使用小推力发动机需要的重定位时间长，一方面影响飞行器的机动特性；另一方面也不一定能最大限度地减少姿控系统燃料的消耗。因此在沉底段考虑使用大推力发动机加速重定位过程。但是大推力发动机的过早介入，有时不仅达不到抑制贮箱内液体晃动的目的，还会使贮箱内的液体晃动加剧。因此，选择变推力时间点让大推力发动机作用适时地介入到重定位过程中是时序优化的关键。

在本次重定位推力时序优化研究中，假设姿控系统仅具有300 N和600 N 2种正向推力的发动机，且发动机不具有脉冲的工作能力。

试验参数包括：模型贮箱直径为0.88 m；柱段长度为0.57 m；四氧化二氮密度为1458 kg/m3；表面张力系数为25.61×10-3N/m；动力粘度系数为0.4189×10-3kg/m•s。该模型参数在300 N推力时邦德数为150左右。

为了选择合理的变推力点，先采用300 N推力完成整个重定位过程，并提取计算过程中能够表征液体运动幅度的轴向重心位置和液体动能随时间的变化曲线，如图4所示。分析中统一采用动能变化曲线稳定低于0.0005时作为重定位运动结束的判据。

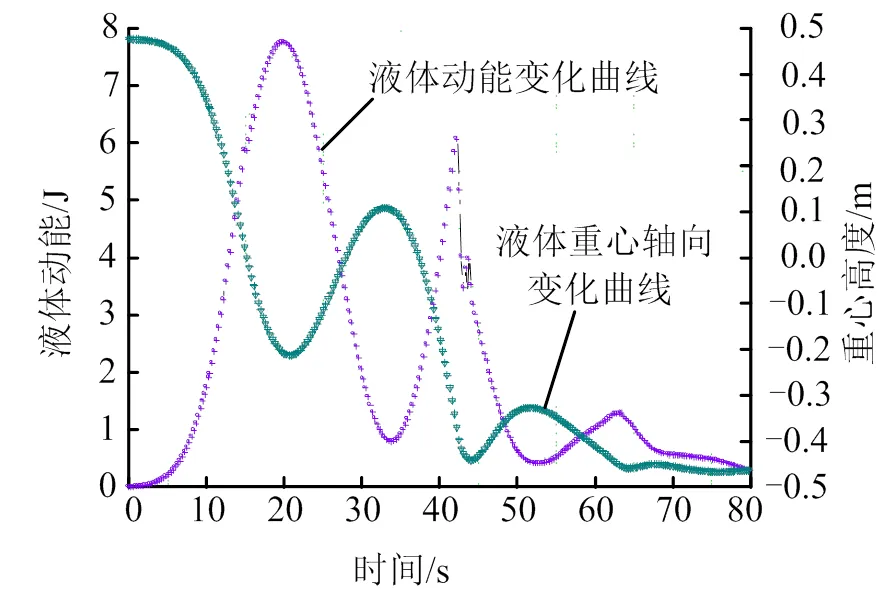
图4 沉底段采用300N推力液体动能和液体重心轴向变化

从图4中可以看到，重定位过程大约耗时75 s。液体重心轴向变化反映液体的势能变化，当动能具有峰值时，重心位置基本上处于极小值位置，符合能量守恒规律。

优化的推力时序，可以从以下4种方式考虑变推力时间点：a）液体基本聚集在箱底后再采用大推力发动机推力，这也是飞行器实际应用中通常采用的方式。从图4中可以看出，在44 s左右是重心位置的极小值点，若在此刻变大推力有利于减小液体整体势能，图5为300 N正推重定位过程中变推力时刻的液体流型图。此时刻液体流型图如图5d所示，液体已经基本上都聚集在箱底；b）大推力发动机提前介入，从减小整体液体势能的角度考虑在重心变化曲线第1个波谷位置 （20 s）施加变大推力，此时的贮箱内流型图如图5c所示，喷泉已经涌起；c）在薄层状流动液体前沿在箱底汇合时刻（14 s）施加大推力，贮箱内流型图如图5b所示，此时液体铺满在贮箱内表面，重心位置位于贮箱的中心位置左右；d）作为对比分析，从一开始就采用600 N大推力沉底，重定位初始状态设定为与 300 N状态一致，起始状态贮箱内流型图如图5a所示。

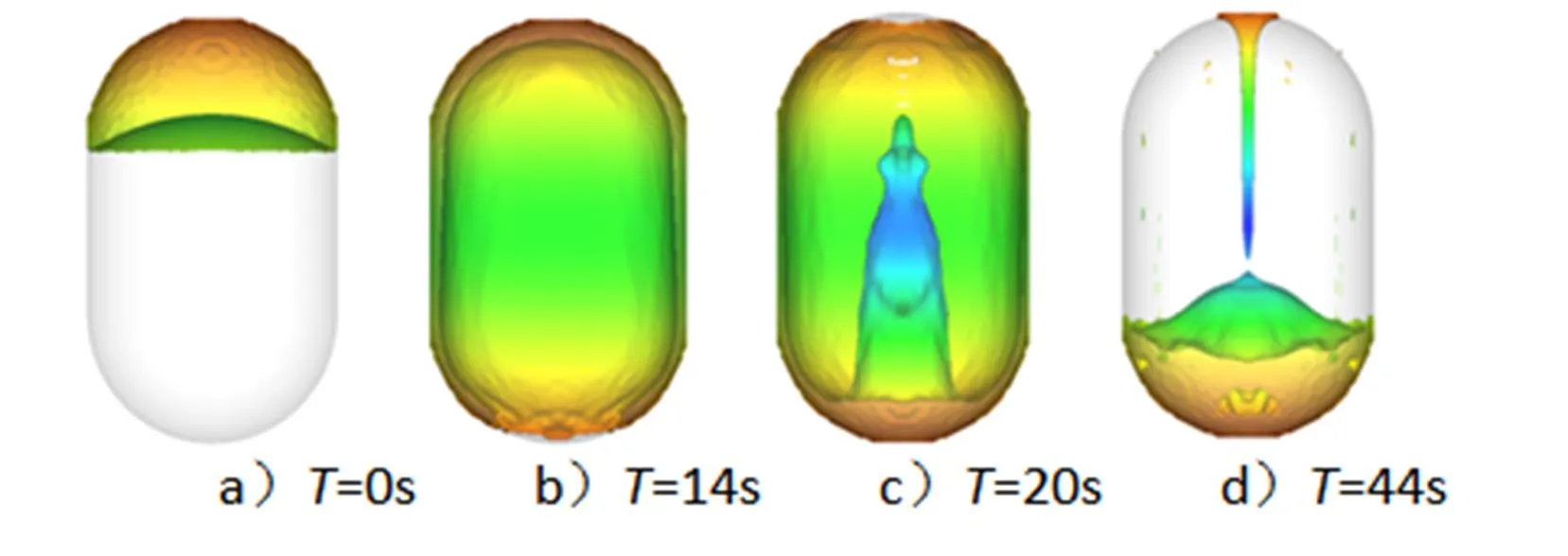
图5 300N正推重定位过程中变推力时刻的液体流型

2种恒定推力方式和3种变推力方式重定位过程中的动能变化如图6所示，时间和能量消耗的对比结果如表1所示。

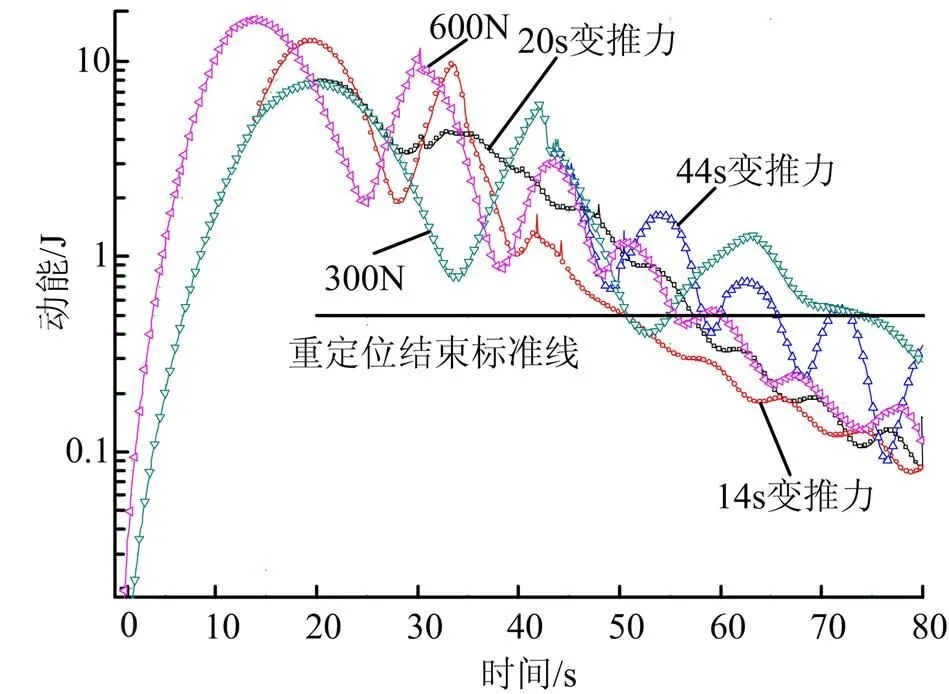
图6 各种重定位推力方式下的液体动能变化

表1 各种重定位推力方式下的时间和能量消耗对比

Tab.1 Comparision of Time and Energy in Various Thrust Modes

参数推力方式重定位时间/s各工况与恒定300N时的重定位时间比值重定位消耗的能量/J各工况与恒定300N时消耗能量的比值 恒定300N751225001 恒定600N600.8360001.6 44s变推力720.96300001.33 20s变推力570.76282001.25 14s变推力500.67258001.15

从重定位的时间上考虑，恒定300 N小推力方式重定位需要的时间最长，但是，恒定600 N大推力重定位的时间却不是最短的，这也验证了上文所述的大推力过早介入重定位带来负面效应的观点。在重心变化曲线波谷位置，变大推力来减少液体整体势能加速重定位过程的方式具有一定的效果，尤其是20 s变推力方式的重定位时间比恒定600 N大推力方式更少。而14 s变推力方式的重定位过程中，液体动能在经历2次波动后迅速下降并达到稳定，其50 s的重定位时间是所有方式中最短的。

从能量消耗的角度分析，恒定300 N小推力重定位过程虽然重定位时间最长，但是消耗的能量却是最少的。而恒定600 N大推力方式最大的能量消耗没有换来最短的重定位时间。20 s变推力方式和44 s变推力方式在能量消耗方面表现优于600 N大推力方式。14 s变推力方式由于重定位时间上的较大优势，消耗的能量仅仅为恒定300 N方式消耗能量的115%，优于其它推力方式。

由于受网格大小的影响，计算过程中只能描述较大气泡（大于3 cm）的析出情况，而更小气泡的析出情况无法模拟。考虑到大推力时气泡析出快于小推力时气泡析出的特点，在计算的重定位结束时刻，14 s变推力方式液体中的气泡析出情况应该优于300 N推力方式，也就是说恒定300 N的推力方式要达到相同的气泡的析出程度还需更长的时间，说明14 s变推力的方式消耗的能量低于恒定300 N重定位消耗的能量。

综合以上分析，在300 N的推力作用14 s之后，变600 N大推力的重定位推力时序不仅能让主发动机最快启动，同时减少姿控系统的燃料消耗，是比较合理的重定位推力时序。通过对14 s变推力重定位时序的重定位过程中的速度云图进行分析，可以得到优化变推力介入时间点的规律，这对重定位时序设计有重要的意义。

图7是14 s变推力方式重定位过程中形成的喷泉时的轴向速度云图。速度云图以液体推力方向为运动正方向。

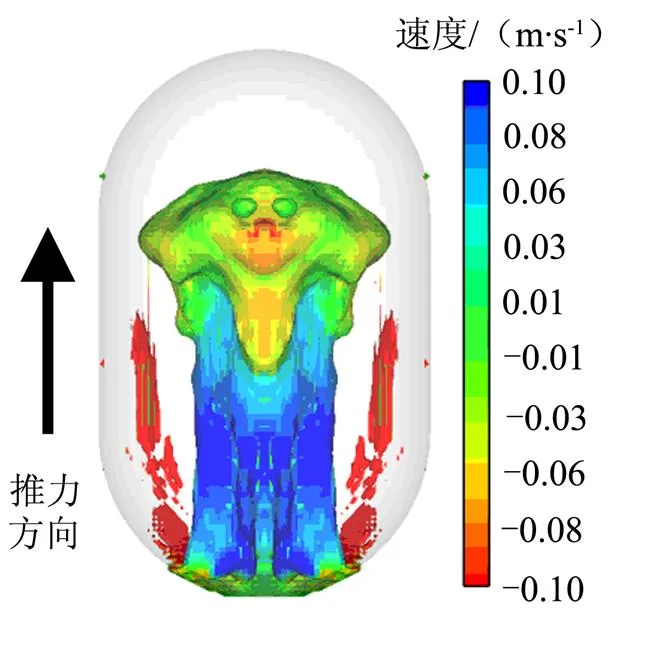
图7 14s变推力方式的喷泉速度云图

从图7中可以看到，此时喷泉的上部已经开始下落，而喷泉的下部则保持向上运动，两股液体的逆向运动在箱体中部形成对冲。从运动区域分布来看，对冲的两股流动动量基本相当，方向相反。两股流动对冲混合之后，箱内液体的总动量将迅速降低，此刻大推力的介入将有效地抑制液体势能和动能之间的转化。通过以上分析可知，当重定位过程重心位于贮箱中心位置时，施加大推力可以在第1次喷泉涌起之后的下坠过程中的一个时间点使箱内的液体具有最小总动量。

如本例计算结果所示，在重定位推力时序设计时将液体重心位于贮箱中心时刻设计为大推力介入时刻可以快速完成重定位并减小能量消耗。

4 时序优化的应用分析

以上计算分析工作是基于某一种贮箱特定的工况，分析在说明通过合理的优化推力时序，可实现快速节能完成液体重定位的一种途径。当液体重定位过程重心位于贮箱中心位置时，施加大推力可以平衡喷泉上涌和下落液体的动量，推力时序优化方法对于贮箱快速节能地完成液体重定位具有一般性。由于推力介入时刻的确定对推进剂本身的物理属性并不敏感[5]，因此认为该推力时序优化方法也可以用于燃烧剂重定位过程。

由于液体重定位是复杂的非线性过程，液体重定位流动形态与推进剂的初始容积以及贮箱的尺寸形状相关，而各飞行器的推力系统组成也不尽相同。因此，在实际应用中重定位推力时序优化设计时，本文中的推力时序优化方法可以作为参考。

对于双组元推进剂系统，燃烧剂和氧化剂的贮箱尺寸和充液比都存在差别，各贮箱液体重定位的特征时刻并不完全同步，需要多方面综合权衡燃烧剂和氧化剂贮箱的具体情况制定重定位推力时序。若燃烧剂和氧化剂质量相差较大时，单从能量的角度来说以质量较大的贮箱作为重定位推力时序优化主要研究对象是比较合适的。

5 结束语

液体重定位由于其运动的复杂性，要通过试验手段比较完整地模拟整个过程，无论是通过地基还是天基试验设备都几乎是不可能完成的。而不受过载和时间约束的数值分析方法逐渐成为液体重定位运动研究的重要手段。

本文通过数值分析方法，对多种推力方式的重定位效果进行对比，证明了恒定的使用大推力或是小推力来完成重定位的方式都不是最理想的，通过合理的优化推力时序，使用变推力的沉底方式，可以达到快速完成重定位同时又达到最小能量消耗的目的。

[1] 刘桢, 褚桂敏, 李红, 王丽霞. 运载火箭上面级微重力环境下的推进剂管理[J]. 导弹与航天运载技术, 2012(4): 20-26.

Liu Zhen, Chu Guimin, Li Hong, Wang Lixia. Propellant management of rocket upper stage in microgravity environment[J]. Missiles and Space Vehicles, 2012(4): 20-26.

[2] 王永志, 王丹阳. 同步通信卫星的发射[M]. 北京: 国防工业出版社, 2005.

Wang Yongzhi, Wang Danyang. The launch of synchronous communication satellite[M]. Beijing: National Defense Industry Press, 2005.

[3] Jaekle D E, Jr. Propellant management device conceptual design and analysis: traps and troughs[R]. AIAA 95-2531, 1995.

[4] Jaekle D E, Jr. Propellant management device conceptual design and analysis: Vanes[R]. AIAA 91-2172, 1991.

[5] 黄怀德, 褚桂敏, 张秀清. 振动工程(下)[M]. 北京: 宇航出版社, 1995.

Huang Huaide, Chu Guimin, Zhang Xiuqing. Vibration engineering(Ⅱ) (M). Beijing: Aerospace Press, 1995.

[6] Jack A S, William J M, Raymond F L. Low-gravity reorientation in a scale-model centaur liquid-hydrogen tank[R]. NASA TN D-7166, 1973.

Thrust Time-series Optimization for Reorientation of Propellant

Liu Zhen1, Wang Li-xia2, Lin Hong3, Lin Ruo1, Zhou Yun-qiang1

(1. Beijing Institute of Space Long March Vehicle, Beijing，100076; 2. Beijing Institute of Structure and Environment Engineering, Beijing, 100076; 3. Beijing Institute of Astronautical Systems Engineering, Beijing, 100076)

In this paper, a numerical simulation method was adopted to study the reorientation of propellant in microgravity environment, and verify the model in correct using the result of drop tower test of the centaur in Lewis Zero-Gravity facility .Based on the numerical simulation method, investigate the thrust time-series optimization of the reorientation of propellant .The result show that, the thrust time-series optimization can accelerate the reorientation and reduce the energy consumption.

Propellant management in microgravity environment; Reorientation of propellant; Thrust time-series optimization

1004-7182(2018)01-0106-05

10.7654/j.issn.1004-7182.20180121

V23

A

2016-03-03；

2017-07-03

刘 桢（1982-），男，高级工程师，主要研究方向为液体动力学