火星飞机的多胞LPV鲁棒控制器设计

关皓天，赵友铖，倪 昆，张庆振



火星飞机的多胞LPV鲁棒控制器设计

关皓天，赵友铖，倪 昆，张庆振

（北京航空航天大学，北京，100191）

随着火星探测的日益发展，火星飞机作为一种中尺度探测手段，能够很好地补充轨道和地表探测器之间的能力空白。针对火星飞机的强非线性、参数不确定性的特点，提出了一种火星飞机的多胞LPV变增益∞控制器设计方法。首先依据火星飞机的纵向非线性模型，在进行研究的飞行包线内选取适量平衡工作点进行雅可比线性化，通过线性化后的线性时不变系统数值拟合得到系统的LPV模型；然后通过张量的高阶奇异值分解理论进行张量积建模，实现火星飞机LPV模型的多胞形表示。最后设计基于LMI求解的鲁棒变增益控制器，使对象能够克服不利特性的影响，能够完成指令信号的快速跟踪并且使系统具有较强的鲁棒性。

火星飞机；高阶奇异值分解；多胞形LPV系统；变增益∞控制

0 引 言

火星探测作为深空探测的重要内容，成为世界各国研究的热点。火星车和轨道卫星对于火星上峡谷山脉等特殊地形的探测存在较大难度，火星飞机作为中尺度探测工具可以利用磁力计、质谱仪、点谱仪等仪器对火星大气及特殊地形表面进行探测完成科研任务[1]。但是火星特殊大气环境为火星飞机控制系统的设计带来了巨大的挑战。火星周围大气层很薄，周围大气的主要成分为二氧化碳和氮气等，实际的大气条件会根据位置，季节和一天的时段具有20%的摄动范围[2]。为了保证火星飞机在复杂飞行环境下的控制性能，一般在控制系统设计中采用鲁棒控制方法。文献[3]提出了一种PI-∞复合控制方法设计火星飞机的控制系统；文献[4]提出了一类混合灵敏度∞控制方法解决了火星飞机的纵向跟踪问题，取得了良好的控制效果。

火星的恶劣的大气环境决定了火星飞机比传统飞行器的控制系统具有更高的控制性能要求。传统变增益控制由于其自身的局限性[5]。显然无法满足火星飞机控制系统的高性能要求。而采用先进控制方法如动态逆，反步法等[6]将面临复杂的设计过程。近年来线性变参数（Linear Parameter Varying，LPV）理论大力发展，基于该理论的变增益控制广泛应用于飞机、导弹、机器人等控制对象中[7]，具有很强的适用性。基于LPV系统的鲁棒变增益控制理论的最大优势是设计控制器时可以对其采用线性控制理论中的方法，通过变参数的调度不仅展现系统的时变性和非线性，同时实现控制器参数的增益调度，弥补了传统变增益控制的不足。

本文针对火星飞机纵向模型，设计巡航飞行任务，建立火星飞机的LPV系统。基于张量积建模理论实现LPV系统的多胞形表示，并提出一种变增益输出反馈∞控制方法，完成火星飞机的纵向跟踪飞行任务。

1 火星飞机LPV建模

1.1 火星飞机模型

火星飞机的纵向非线性模型[8]为

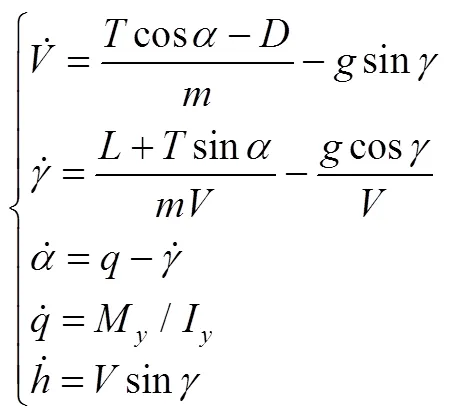
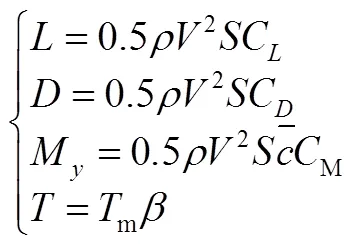
火星飞机的发动机可用一个二阶环节表示：

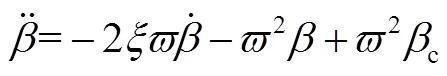
由于火星飞机是一个复杂的非线性系统，且飞行环境特殊，为了便于研究做出以下假设：a）忽略火星曲率；b）飞机几何外形对称，内部质量分布对称；c）忽略操纵面的转动惯量，忽略推进剂晃动；d）火星飞机在飞行过程中无横侧向运动。

1.2 多胞LPV建模

构建一个非线性系统的LPV模型首先要确定变参数即调度参数，通常情况下可选取高度、速度作为飞行控制系统的调度参数。尽管一个非线性模型的LPV表示不是唯一的，但是基于雅可比线性化的LPV建模是最简单直观的，其适用对象广泛、求解思路清晰。本文拟采用基于雅可比线性化的方法是实现LPV建模。雅可比线性化的基础是泰勒级数展开，给定一个非线性系统，有：

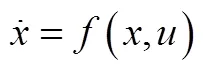
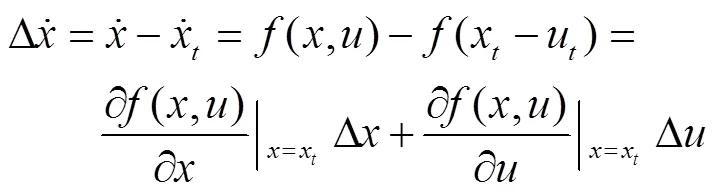
由此得到模型线性化的状态空间表达式：

在该飞行包线内选取一定数量的平衡点，对其进行雅可比线性化，将得到等数量的线性时不变系统（Linear Time Invariant，LTI），选取速度和高度作为变参量，选取合适阶数的拟合函数，对这些LTI进行数值拟合可得到火星飞机的LPV模型。

分析得到的上述多个雅可比矩阵，选择合适阶数的拟合函数，对LTI模型进行数值拟合，可以得到以高度和速度为变参量的火星飞机LPV模型：

由于LPV系统是由无数个LTI组成，在应用线性鲁棒控制理论设计控制器时，为了避免求解变参数轨迹上无数个线性矩阵不等式（LMI），需要将原LPV系统转化成具有凸性质的多胞形结构，从而将原LPV系统以有限的顶点完全描述，大大减小了求解控制器参数过程中的计算量。

目前，基于张量高阶奇异值分解（High Order Singular Value Decomposition，HOSVD）理论[9]的张量积建模法是求取多胞顶点的一种有效途径。首先将离散的LTI存储到高阶张量中，并对其进行HOSVD舍去较小的奇异值和相关奇异向量，将筛选得到的有限顶点系统表示成张量积的形式：

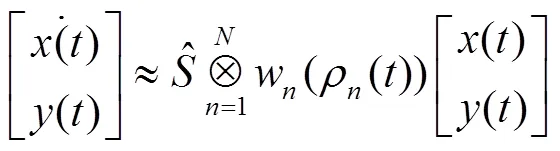
（9）

这样可以将式（7）的LPV系统转化为有限个顶点系统的多胞组合形式：

2 火星飞机的鲁棒变增益控制器设计

对于火星飞机LPV模型的多胞形表示式（10）, 可将其顶点系统表示成如下的状态空间：

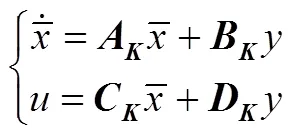
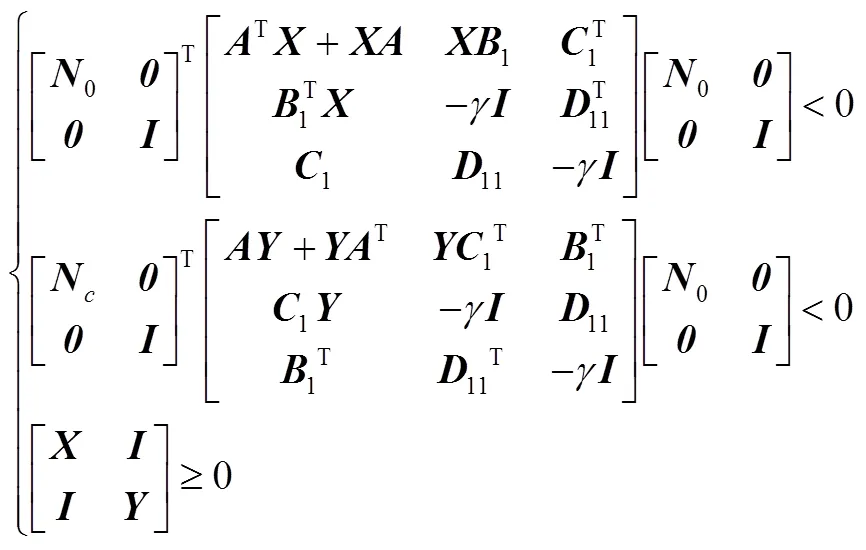
根据顶点性质[12]，飞行包线内任意工作的控制器参数可通过时变参数对顶点系统加权调度求解实现：

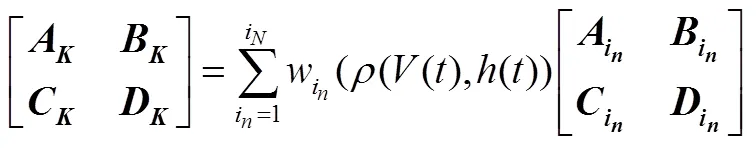
3 仿真分析

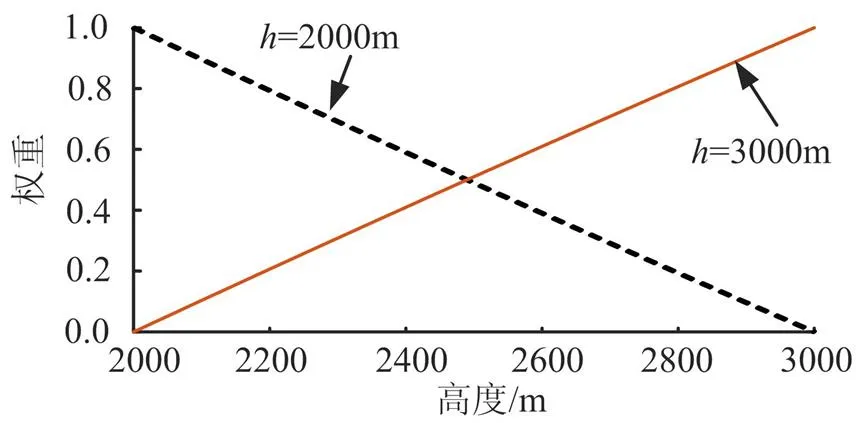
图1 调度参数高度的权重函数

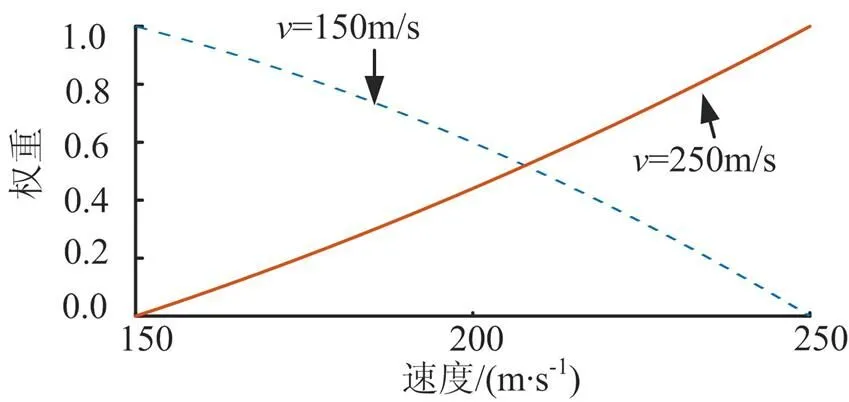
图2 调度参数速度的权重函数

图3 火星飞机控制系统结构

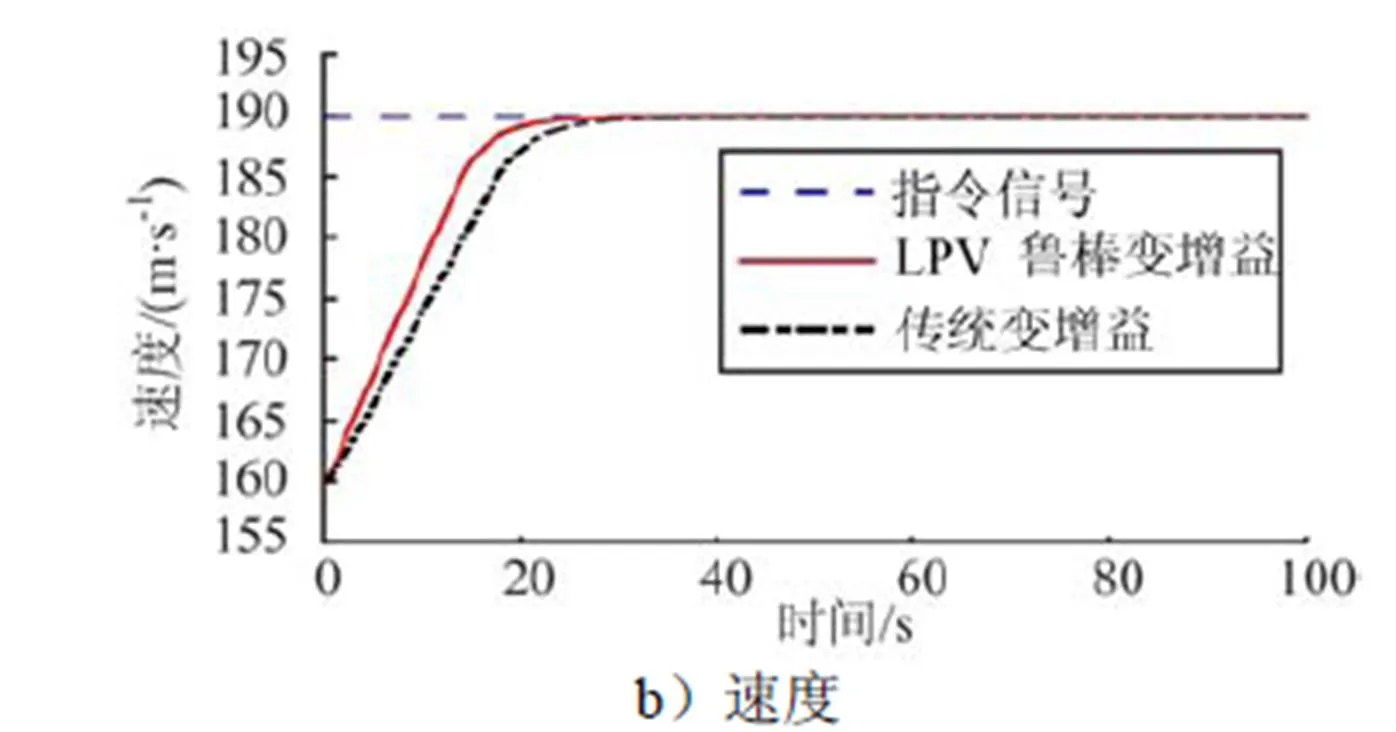
为了验证LPV鲁棒变增益控制器的控制性能，将其与传统变增益控制方法的效果进行比较，图4为标称模型下火星飞机的高度和速度的响应跟踪曲线。

图4 标称模型中高度和速度响应曲线

Fig.4 Curves of Height and Velocity in Nominal

续图4

考虑到火星飞机气动参数的大范围摄动和飞机参数的不确定性，首先给出飞机不确定范围为

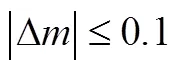
再给出气动参数的不确定范围为

针对火星飞机及气动参数的标称模型，定义其不确定参数上限和下限模型并给定相同的跟踪指令信号，得到在参数不确定条件下火星飞机的响应曲线，见图5、图6。

图5 不确定参数上限模型中高度和速度响应曲线

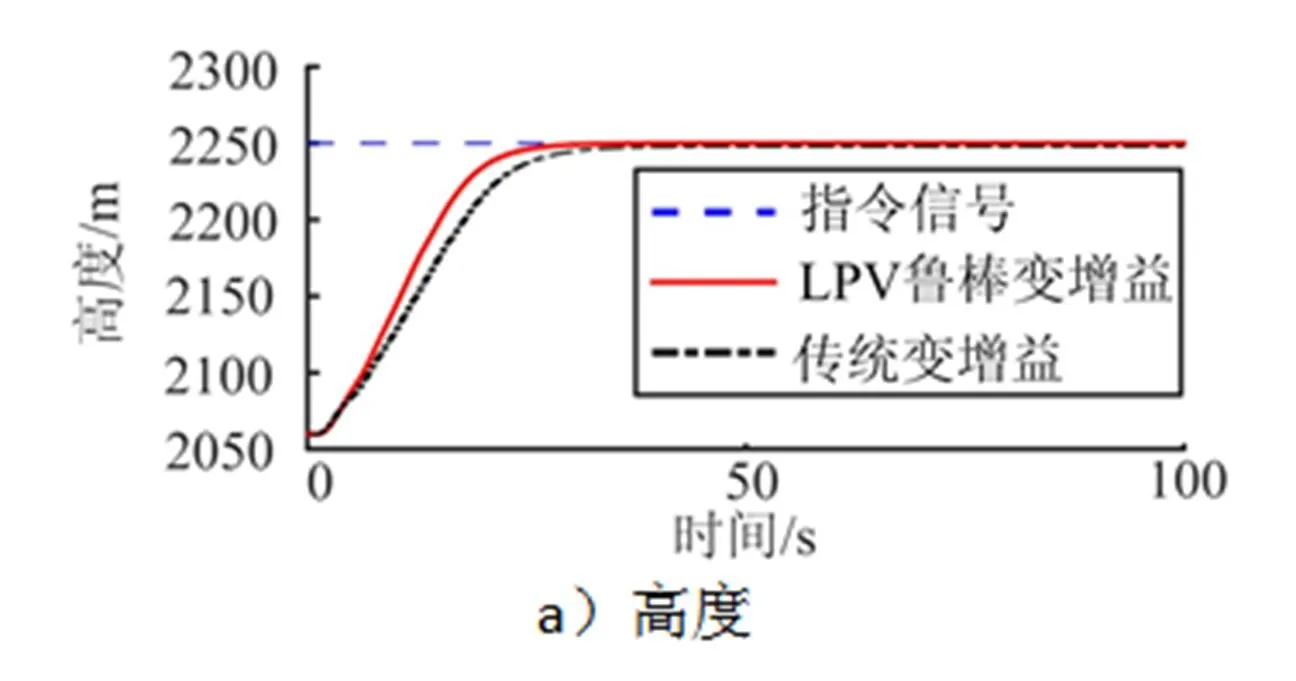
图6 不确定参数下限模型中高度和速度响应曲线

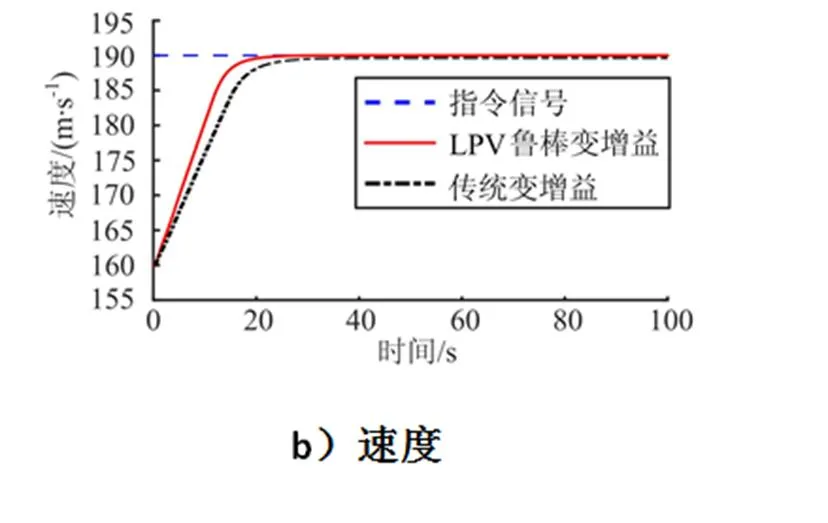
续图6

以上仿真结果表明：在标称模型下两种控制器都能使火星飞机快速跟踪指令信号，但是多胞LPV鲁棒变增益控制器的调节时间更短；在参数摄动的条件下，传统变增益控制将导致飞机产生跟踪误差，控制效果变差；相比而言，多胞LPV鲁棒变增益控制器的稳态误差更小，控制效果更好。说明设计的多胞LPV鲁棒变增益控制器具有较强的鲁棒性和较高的控制精度。

4 结 论

本文针对火星飞机纵向非线性模型，利用雅可比线性化方法拟合LPV模型，基于张量的HOSVD理论得到LPV模型的多胞形表示，并设计了变增益输出反馈∞控制器，通过仿真验证了基于张量HOSVD理论得到的多胞形LPV模型在误差允许范围内可以近似表示原系统；根据顶点性质设计的鲁棒变增益控制器可以通过变参数在线调度完成整个飞行包线内的控制任务，使得所设计的控制器能够较快地跟踪指令信号并具有较强的鲁棒性。

[1] Braun R D, Wright H S, Croom M A. Design of the ARES Mars airplane and mission architecture[J]. Journal of Spacecraft and Rockets, 2006, 43(5): 1026-1034.

[2] Justus C. A Mars global reference atmosphere model (Mars-GRAM) for mission planning and analysis[C]. Atlanta: AIAA, Aerospace Sciences Meeting, 2013.

[3] Hjartarson A, Paw Y, Chakraborty. A modeling and control design for the ARES aircraft, model-based aerospace challenge[C]. Hawaii: AIAA Guidance, Navigation and Control Conference and Exhibit, 2013.

[4] Bhattacharya R, Valasek J. On modeling and robust control of ARES[C]. Hawaii: AIAA Guidance, Navigation and Control Conference and Exhibit, 2008.

[5] 李文强. LPV系统鲁棒变增益控制研究及应用[D]. 长沙: 国防科技大学，2004.

Li Wenqiang. Reaearch and application of robust gain-scheduling based on LPV system[D]. Changsha: National University of Defense Technology, 2009.

[6] 宋超, 赵国荣, 盖俊峰. 基于非线性干扰观测器的高超声速飞行器反演滑模控制[J]. 系统工程与电子技术, 2012, 34(6): 1231-1234.

Song Chao, Zhao Guorong, Gai Junfeng. Sliding mode backstepping control for hypersonic aircraft based on nonlinear disturbance observer[J]. Systems Engineering and Electronics, 2012, 34(6): 1231-1234.

[7] Liu Y, Peng K. Flight control law using composite nonlinear feedback technique for a Mars airplane[J]. Journal of Guidance Control and Dynamics, 2016, 39(9): 1-9.

[8] 张少康. 基于 LPV 模型的高超声速飞行器鲁棒预测控制方法研究[D]. 天津: 天津大学, 2014.

Zhang Shaokang. Research on robust model predictive control based on LPV model for hypersonic vehicles[D]. Tianjin: Tianjin University, 2014.

[9] Petres Z. Polytopic decomposition of linear parameter-varying models by tensor-product model transformation[J]. Dissertation, 2006.

[10] 俞立. 鲁棒控制-线性矩阵不等式处理方法[M]. 北京: 清华大学出版社, 2002.

Yu Li. Robust control: linear matrix inequalities (LMI) treatment[M]. Beijing: Tsinghua University Press, 2002.

[11] Apkarian P, Gahinet P, Becker G. Self-scheduled H∞control of linear parameter-varying systems: A design example[J]. Automatica, 1995, 31(9): 1251-1261.

Robust Variable Gain Control for Mars Airplane Based on Polytopic LPV

Guan Hao-tian, Zhao You-cheng, Ni Kun, Zhang Qing-zhen

(Beijing University of Aeronautics and Astronautics, Beijing, 100191)

XWith the increasing development of Mars detection, Mars airplane as a mesoscale detection means, can be a good complement to fill the ability blank between the track detector and the surface detector. Considering the strong nonlinearity and parameter uncertainty of Mars aircraft, a variable gain∞control method for Mars airplane based on polytopic Linear Parameter Varying (LPV) system is proposed.Firstly,according to the longitudinal nonlinear model of the Mars aircraft, appropriate balance of work points are selected to conduct Jacobian linearization,the LPV model is obtained by numerical fitting of the LTI systems. Then,the tensor product model is carried out by High Order Singular Value Decomposition (HOSVD) theory of tensor,completing the polytopic representation of the LPV model. Finally, a robust variable gain controller based on LMI solution is designed, which can overcome the negative effects and complete the fast tracking of command signal so that the system has strong robustness.

Mars airplane; High order singular value decomposition; Polytopic LPV system; Variable gain control

1004-7182(2018)01-0069-05

10.7654/j.issn.1004-7182.20180114

V448.22+2

A

2017-03-01；

2017-06-22

关皓天（1993-），男，硕士研究生，主要研究方向为导航、制导与控制