独塔单索面单边受拉曲梁斜拉桥受力性能分析

李睿智，王立彬,*，王鹏展，刘文峰

0 引言

1979年冯先沛［1］首先在国内介绍了美国一座曲线型斜拉桥设计方案，虽然这座桥最后没有被建成实桥，但此桥巧妙的设计大大扩宽了桥梁设计的思路；1990年刘蓬风［2］介绍了日本一座S形曲线斜拉桥的抗风抗震分析和设计，该桥是世界首座S形曲线斜拉桥；1998年日本设计师KyoTakenouchi［3］首次讨论了独塔曲线斜拉桥，介绍了独柱塔的美学效应以及应用于曲线斜拉桥的诸多优势；1999年Jeffery Lee等［4］通过有限元模型对新加坡safti Link桥进行了动力分析，并在随后展开了一系列研究，safti Link桥是世界上第一座单索系短跨非对称曲线斜拉桥，是曲线斜拉桥发展中的一座里程碑；2000年孙传洲［5］介绍了瑞士一座曲线斜拉桥的实桥试验、模型试验及结构分析，研究表明斜拉结构可以用于曲线桥，但力

1.2 单索面曲梁斜拉桥斜拉索的传力特征

拉索两端分别锚固于主梁和塔顶，拉索和主梁由于空间效应形成各种角度，拉索布置对主梁受力有较大的影响。

当塔顶锚固点位于圆心正上方时，斜拉索的水平分力Ni,H指向圆心，相当于给主梁施加了压力，如图3（a）所示；当塔顶锚固点偏向主梁时，斜拉索的水平分力Ni,H可以分解为垂直于主梁的分力Ni,HV和与主梁相切的分力Ni,HT，这两个分力相当于共同给主梁施加了压力，如图3（b）所示；当塔顶锚固点远离主梁时，斜拉索的水平力Ni,H同理也可以分解为垂直于主梁的分力Ni,HV和与主梁相切的分力Ni,HT，但此时Ni,HV所转化给主梁的压力与Ni,HT给主梁施加的拉力方向相反，如图3（c）所示，合力是压力还是拉力取决于斜拉索的具体布置。

当塔顶锚点位于曲线外侧时，斜拉索的水平分力NO,H同理也可以分解为垂直于主梁的分力NO,H,V和与主梁相切的分力NO,H,T，NO,H,T相当于给主梁施加了压力，但NO,H,V的方向则不固定，如图3（d）所示，NO,H,V的方向临界变化条件是最外一根斜拉索水平投影与主梁线形是否相切。若投影在圆弧内，则NO,H,V方向指向圆心，与其他斜拉索在主梁锚点的分力方向相反，容易造成较大的主梁横向弯矩；若投影与圆弧相切，则NO,H,V为零；若投影在圆弧外，则NO,H,V方向远离圆心，且与其他斜拉索在主梁锚点的分力方向相同。

以上分析表明，若斜拉索布置的合理，曲梁与斜拉索的结合，可以大大减小多余水平分力所造成的主梁横向弯矩。

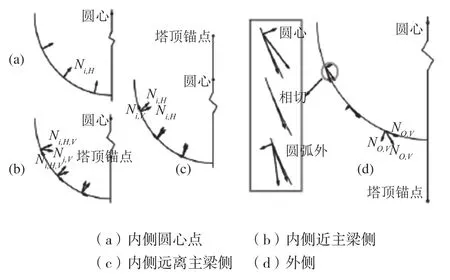
图 3 斜拉索主塔锚固位置水平效应示意图Fig.3 Influence of the horizontal force induced by cable-tower anchor point

1.3 单索面曲梁斜拉桥曲线主梁抗扭措施

为了抵抗扭矩，可以通过以下三种方式，分别为施加环向预应力方法、采用偏心截面法和锚固位置调整法：

（1）施加环向预应力方法如图4（a）所示，当斜拉索面在梁曲线外侧时，索力NO的垂直分力NO,V和重力G产生扭转力TO,1，为了抵抗这个扭转力，增大主梁横截面高度，并在主梁下部引入水平力PC。水平力PC与索力NO的水平分力NO,H,T产生扭转力TO,2，这两个扭转力方向相反，可达到主动抵抗扭转的目的。水平力PC可以通过对梁下部施加压力C实现。

同理，如图4（b）所示，当斜拉索面在梁曲线内侧时，可以通过对主梁下部施加拉力S，由此产生的水平力PS与索力Ni的水平分Ni,H力产生扭转力Ti,2，达到抵抗索力Ni的垂直分力Ni,V和重力G产生扭转力Ti,1的作用。

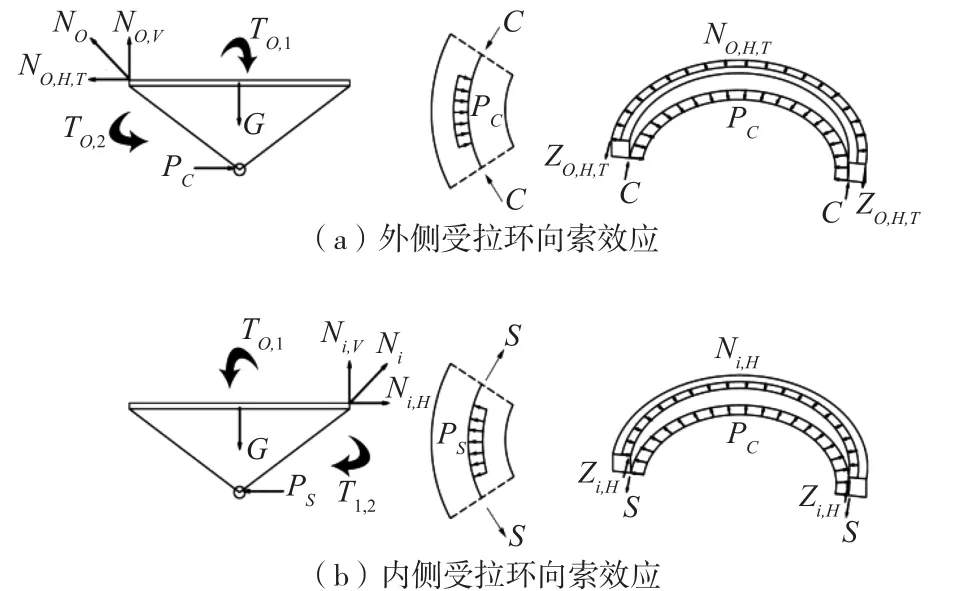
图 4 环向索效应示意图Fig.4 Effect of hoop cable

（2）采用偏心截面法如图5所示，该方法通过采用偏心截面主梁而非对称型主梁截面，减小力臂的大小，达到减小扭矩的作用。

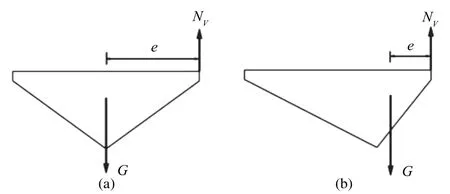
图 5 主梁横截面变化导致重心变化Fig.5 Gravity center change induced by beam cross section change

（3）锚固位置调整法如图6所示，该方法通过主动利用扶手栏杆等刚性杆件，改变斜拉索主梁的实际锚固位置，但其延伸线尽可能接近截面中心，以减小力臂大小，达到减小扭矩的作用。

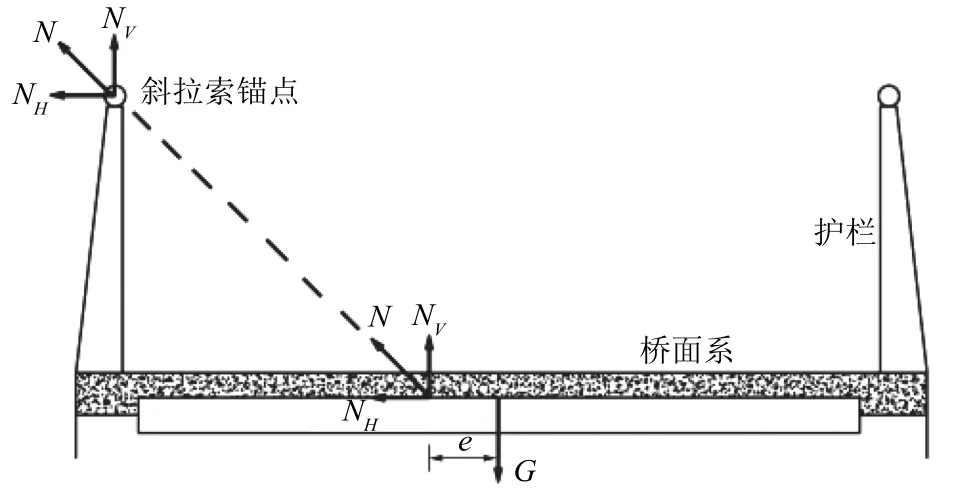
图 6 斜拉索-主梁锚固位置引起力臂减小Fig.6 Force arm reduced by change of the cable-beam anchor point

1.4 桥型设计

根据以上基本力学特征分析，设计一曲线斜拉桥并进行参数分析。

桥梁平面位于曲线半径100 m、圆心角90°的圆曲线上。直线跨度141.42 m，沿曲线跨度157.08 m，桥面宽度7m。综合考虑斜拉桥结构的受力特点和整体空间效果，桥塔设计标高为52.2 m，与水平面夹角80°。主塔与主梁仅通过斜拉索联系。斜拉索采用辐射形布置，索面呈抛物面。内侧单边受拉时，梁上索距间隔9 m，全桥共16根斜拉索；外侧单边受拉时，梁上索距间隔9.6 m，全桥共16根斜拉索。如图7（c）和图7（d）所示。

桥面系在单侧拉索作用下，横向受力是整个结构的关键受力之一，应尽可能降低索力，减小斜拉索径向力对主梁的不利影响，因此可选择钢箱梁这种自重较小的主梁形式；自重引起的扭转是整个结构的另一个关键受力，因此底板向索梁锚固侧偏移，从而改变截面重心。顶板、底板、纵向肋均采用Q345，24 mm厚钢板，钢箱梁各板件连接全部采用焊接形式，如图7（a）所示。

桥塔将承受较大竖向压力，为了增加桥塔的刚度和稳定性，桥塔主体采用钢管混凝土组合截面，钢管截面直径为1 200 mm，壁厚为10 mm，内置T型肋，采用Q345钢，钢管内部采用C30混凝土浇筑，如图7（b）所示。

斜拉索采用直径为7 mm的低应力平行镀锌钢丝索体，极限强度为1 670 MPa。

2 有限元模型的建立与分析方法

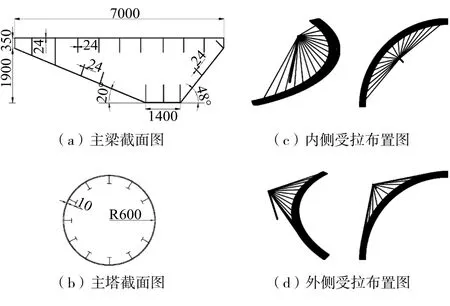
图 7 桥梁截面与布置（mm）Fig.7 Cross section and layout of the bridge

采用Midas/civil有限元软件建立桥梁的空间模型，钢箱梁、桥塔采用梁单元，斜拉索采用桁架单元。结构共划分为85个单元，塔底与支座固接，索梁为铰接。在软件中建立自重荷载工况，设定重力加速度9.805 m/s2，桥面铺装恒载0.5 KN/m2。

斜拉桥是高次超静定结构，斜拉索合理索力值存在多组方案，确定合理成桥状态的方法有多种，本文采用分步算法以融合多种算法确定合理成桥状态，具体为：先用最小弯曲能量法初定成桥状态；然后以应力平衡法确定主梁成桥恒载弯矩“可行域”；最后用影响矩阵法确定综合考虑主梁、塔和索等结构受力要求的合理成桥状态［9］。

3 受力特征参数分析

通过改变独塔单索面单边受拉曲线斜拉桥主塔位置、索梁锚固位置、索塔锚固位置，分析曲线梁特有成桥状态下结构轴力、扭矩及横向、竖向弯矩的变化，通过设置环向索对比分析结构扭转的影响。

3.1 主塔锚固点偏移影响分析

内侧受拉曲线斜拉桥斜拉索主塔锚固偏移布置如图8（a）1～7号点所示，即分别布置在弦内1个，弦外1个，圆心靠主梁一侧2个，圆心1个，圆心远离主梁2个，共7个点。

外侧受拉曲线斜拉桥斜拉索主塔锚固偏移布置如图8（b）1～5号点所示，分别布置在最外侧斜拉索切线靠近主梁一侧2个，切线位置1个，最外侧斜拉索切线远离主梁一侧2个，共5个点。

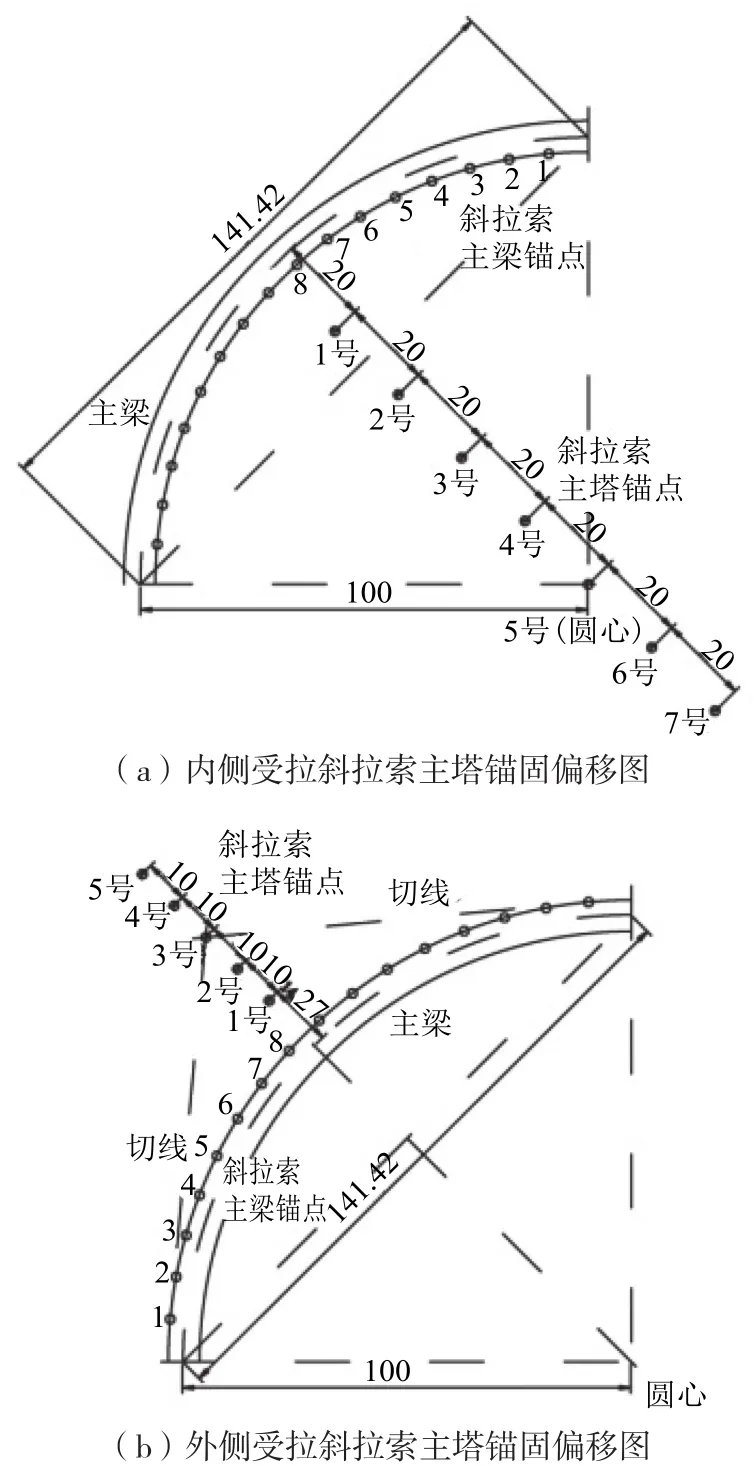
图8 斜拉索主塔锚固点偏移图(m）Fig.8 Arrangement of cable-tower anchor point

建立7个模型进行分析，分析结果如图9所示，内侧单边受拉的主梁，全梁截面承受压力。压力趋势为：当锚固点位于圆心靠主梁一侧时，压力两边小中间大；当锚固点位于圆心远离主梁一侧时，压力中间小两边大；锚固点位于圆心时，压力较为均匀，如图9（a）所示。这是因为随着主塔锚固点的偏移，斜拉索水平分力的切向分力方向发生了改变，方向变化的临界位置为圆心，切向分力由压力变化为拉力，从而减弱了梁压力。

如图9（b）所示，扭矩表现出反对称分布，曲梁对称面上扭矩几乎为零，随着主塔锚固点远离主梁，扭矩的正负发生了变化，5号锚固形式即当索塔锚固点位于圆心时，成为临界位置，此种情形下主梁扭矩趋于零，如1.2节分析，这是因为此时斜拉索的延长线几乎穿过主梁各横截面重心，从而大大减小了结构几何上的偏心所导致的扭转。

弯矩方面，随着主塔锚固位置远离主梁，跨中竖向弯矩部分从负值逐渐变化为正值，横向弯矩也由下凹形状变为上突形状，横向和竖向弯矩表现出类似的趋势。综合内力分布情况，可见4号位置为一个内力分布的最优布置点。

外侧单边受拉的主梁，承受拉力。拉力趋势为：均为跨中间小两边大，如图9（a）所示。这是因为斜拉索水平分力的切向分力方向不随主塔锚固点位置的偏移而发生改变。主梁扭矩为反对称，5种方案扭矩分布基本趋势有较好的一致性。

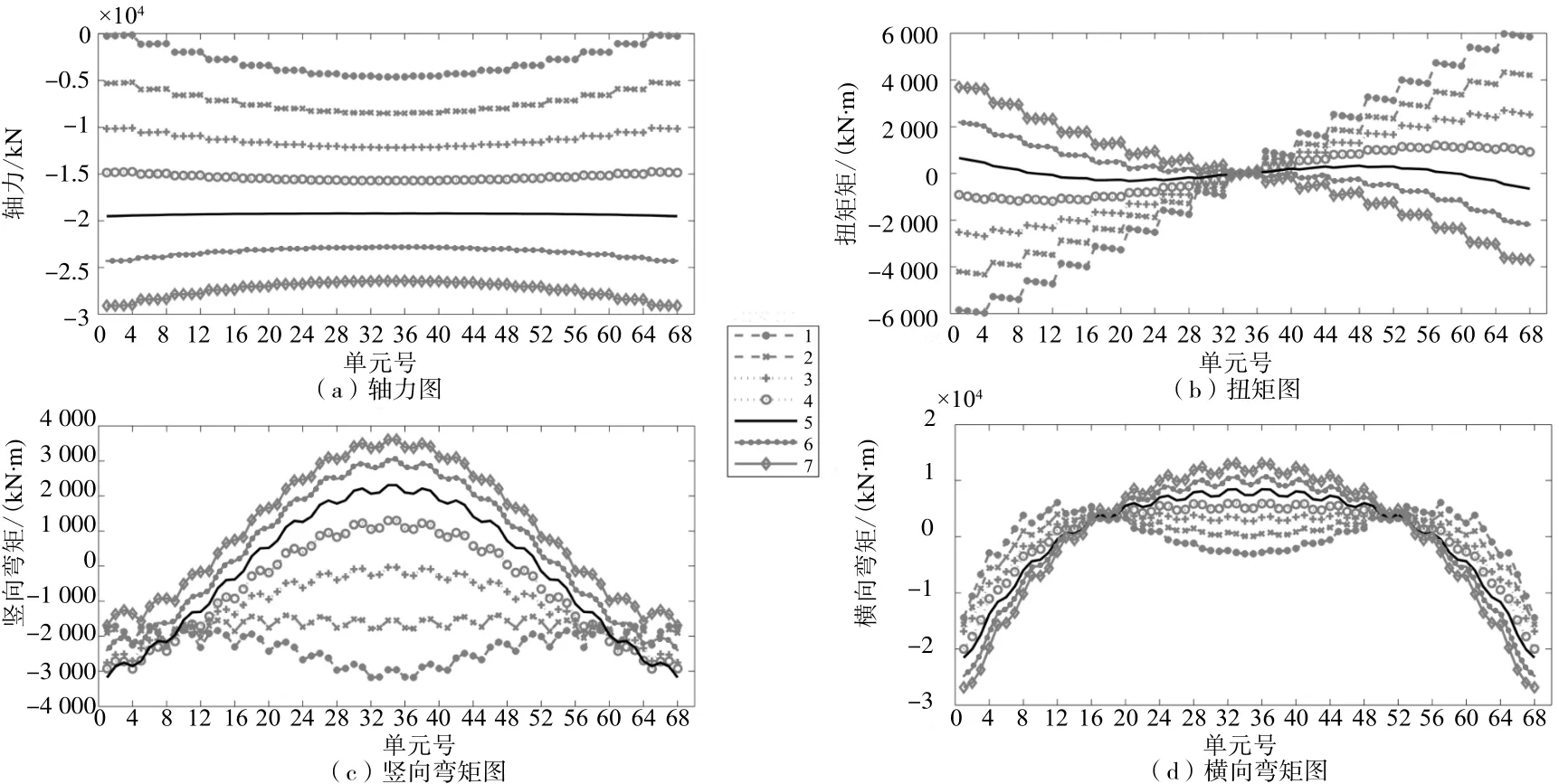
图 9 内侧受拉斜拉索主塔锚固点偏移影响Fig.9 Influence of inner cable-tower anchor point arrangement

主梁竖向弯矩在边跨处为负弯矩而中跨处为正弯矩，各种布置方案下弯矩分布形式一致，幅度变化不大。主梁横向弯矩差随主塔锚固点偏移量的增加而增加，且以“切点”为临界位置，内外的弯矩差显著增大，如图10（d）所示。这是因为随着主塔锚固点的偏移，斜拉索水平分力的径向分力方向发生了变化，方向变化的临界位置为“切点”，从而增加了横向弯矩差。在主梁四分之一处，5种方案的横向弯矩相近，为弯矩不敏感区域。综合而言，外切交合点位置为一个理想的上锚点位置。

3.2 环向索影响分析

水平环索采用φ115 mm的大直径密闭索，强度为1 670 N / mm2，沿桥梁弧形分布于主梁底部，两端锚固于基础，与主梁采用弹性连接的刚性连接相连接，如图11所示。力变为拉力，主梁仍然以压力为主，对于扭矩而言，除环向索在端部有一定的改善作用外，主梁大部分位置与不施加环向索的情形一致。

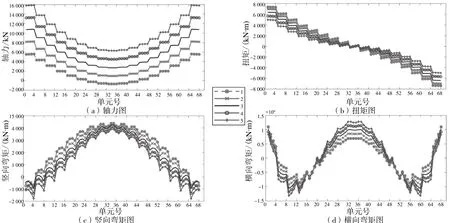
图 10 外侧受拉斜拉索主塔锚固点偏移影响Fig.10 Influence of outer cable-tower anchor point arrangement

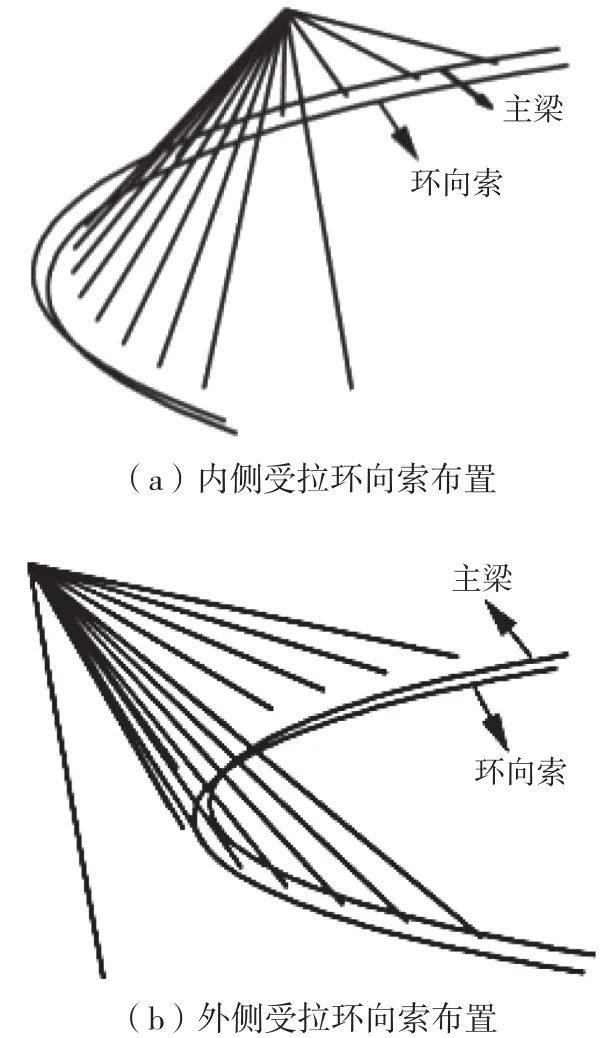
图 11 环向索布置示意图Fig.11 Arrangement of hoop cable

对于外侧单边拉吊形式斜拉桥，施加环向预应力，除端部轴力外其余都有一定程度的改善，但对于外侧拉吊情形，环状索对曲线梁内力改善不大。

4 结论

分析得出，对于内侧单边拉吊形式斜拉桥，环向索的布置可以在曲线主梁的两个端部显著减小横向弯矩，在所有梁截面内一定程度上改善了主梁竖向弯矩，对轴力而言，曲梁端部小范围内轴力由压

本文以一位于半径100 m的圆曲线上，直线跨度141.42 m，桥面宽度7 m的钢管混凝土组合截面曲梁斜拉桥为模型，运用Midas/civil软件建立了7个外侧受拉曲梁斜拉桥有限元模型和5个外侧受拉有限元模型，分别计算分析了主塔锚固点位置偏移和设置环向索对内、外侧单边受拉曲线主梁受力的影响，研究了曲梁斜拉桥斜拉索、主塔和主梁的不同布置形式对桥梁受力产生的影响，最终得出了以下结论：

（1）拉索与曲线梁的空间角度关系对结构产生重要影响，对于内侧独塔单索面单边受拉曲线斜拉桥而言，上锚点在曲线梁圆心处位置为曲线梁内力分布变化的临界位置。对轴力、扭矩、横弯和竖弯弯矩分布而言，存在最佳锚固位置，且位于圆心内侧。

（2）对于外侧独塔单索面单边受拉曲线斜拉桥而言，内力分布方式随着上锚固点的位置变化的趋势基本一致，仅仅是幅值大小的不同。

（3）环向索可以改善内侧独塔单索面单边受拉曲线斜拉桥的内力分布，但是对于外侧独塔单索面单边受拉曲线斜拉桥而言，效果不明显。

［1］冯先沛.曲线型斜拉桥简介［J］.中国铁路, 1979(21): 22-24.

［2］刘蓬风.一座S形曲线斜拉桥的抗风抗震分析和设计［J］.世界桥梁, 1990(1): 46-54.

［3］Takenouchi K. Single pylons for curved cable-stayed bridges［J］.Structural Engineering International, 1998, 8(4): 269-272.

［4］Brownjohn J M W, Lee J, Cheong B. Dynamic performance of a curved cable-stayed bridge［J］. Engineering Structures, 1999, 21(11): 1015-1027.

［5］孙传洲.曲线斜拉桥的实桥试验、模型试验及结构分析［J］.国外桥梁,2001(1):15-19.

［6］李正仁, 刘祖国.曲线斜拉桥的应用与展望［J］.钢结构,2003, 18(6): 43-45.

［7］马路, 张崇厚.一单索系曲线斜拉桥的结构分析［J］.河北建筑科技学院学报自然科学版, 2007, 24(2): 4-7.

［8］康厚军,赵跃宇,杨相展.弯斜拉桥中索的主共振研究［J］.工程力学,2008(11):86-91.

［9］孙测世, 童建胜, 周水兴.曲线斜拉桥锚固点与支座偏移受力影响［J］.重庆交通大学学报(自然科学版), 2009,28(3): 492-496.

［10］刘铁林,许传贵,刘泓.斜拉弯桥有限元分析模型的对比研究［J］.沈阳建筑大学学报(自然科学版),2010,26(5):838-842.

［11］刘乐天.独塔单索面曲线地铁斜拉桥关键技术研究［J］.都市快轨交通, 2011, 24(6): 72-76.

［12］丁磊, 单宏伟, 郑纪研.独塔双索面曲线斜拉桥钢箱梁设计［J］.现代交通技术, 2011, 8(2): 44-46.

［13］辛连春.一单索面曲线斜拉人行桥结构的分析与设计［A］.2011全国钢结构学术年会论文集［C］.北京:中国钢结构协会,2011:154-158.

［14］Bursi O S, Kumar A, Abbiati G, et al. Identification, model updating, and validation of a steel twin deck curved cablestayed footbridge［J］. Computer-Aided Civil and Infrastructure Engineering, 2015, 29(9): 703-722.

［15］徐佰顺, 钱永久, 李豹, 等.大跨径曲线矮塔斜拉桥参数敏感性分析［J］.世界桥梁, 2016, 44(5): 62-66.

［16］丁幼亮,卞宇,赵瀚玮,等.公铁两用斜拉桥竖向挠度的长期监测与分析［J］.铁道科学与工程学报,2017,14(2):271-277.

［17］丁幼亮,周凯,王高新,等.苏通大桥斜拉桥伸缩缝位移的长期监测与分析［J］.公路交通科技,2014,31(7):60-64.

［18］李睿智.独塔曲线斜拉步行桥力学性能研究［D］.南京: 南京林业大学, 2017.

［19］董伟,杨华.波形钢腹板多箱结合独塔斜拉桥的受力分布研究[J].公路工程,2017,42(6):128-131.