基于ROC-SVD的轴承故障检测*
2018-03-20于洪兵张亚岐周副权陈重均
于洪兵 张亚岐 周副权 陈重均
(①包头职业技术学院, 内蒙古 包头 014030;②东风汽车公司技术中心,湖北 武汉 430058)
轴承在机械传动过程中起到支承作用,其可靠性关系到整个传动系统的正常运转。其结构要求严格,但由于轴承工作环境复杂,润滑条件受温度影响较大,在密封不好的传动系统中,轴承很容易出现失效,造成传动系统瘫痪。目前车载诊断系统能够对车辆实现全方位的故障检测,对可能出现的故障提前预警,在一定程度上改善了现有车辆的行驶安全性和可靠性,而轴承作为机械传动的核心部件,被称之为机械“关节”,因此滚动轴承的正常运转直接制约着整个系统的运行。在通常工程实际运行过程中,由轴承故障造成的事故屡屡发生[1]。在此,需要了解、掌握轴承结构和它的故障机理的理论基础上,对其进行及时、正确的检测与诊断分析,从而预防故障的扩大化,延长整个机械系统正常运行周期,进而提高生产经济效益。
由于滚动轴承在工作过程中受到振动影响,故障信号与承载轴振动信号频率接近,故障信号很容易被吞没。在故障初期表现最为突出,传统的常规手段很难将信噪分离,而检测出早期的故障信号对提升整个传动系统的可靠性才有意义。因此,在轴承故障发生初期,利用信号提取技术将故障合理有效的故障特征提取出来,并结合信号处理技术,给出当前故障所处阶段,判断是否需要采取相应措施,这些均已成为故障诊断系统的关键技术。奇异值分解[2](singular value decomposition,SVD)是一种理想的去相关性理论,该理论在检测信号同时提取周期成分,根据奇异值能量的贡献率来判定奇异值的有效性,并通过奇异值的重构来提取故障信息。在奇异值分解时,奇异值阈值选择的随意性对检测结果有一定影响,在对低信噪比或者融合多个故障信号检测时,阈值选择的影响更为显著。为了最大限度的降低奇异值阈值对检测结果的影响,本文采用受试者特征工作曲线(ROC曲线)对初选的阈值进行优化,保证相邻两个时窗的故障频率误差不超过5%,从而提升实时在线检测的准确率。
1 基本理论
1.1 奇异值能量
对于一个离散数字信号X=(x(1),x(2),…,x(N)),其中,1,2,…,N分别是采样点数,对信号X进行Hankel矩阵构造,构造具体内容如下:
(1)
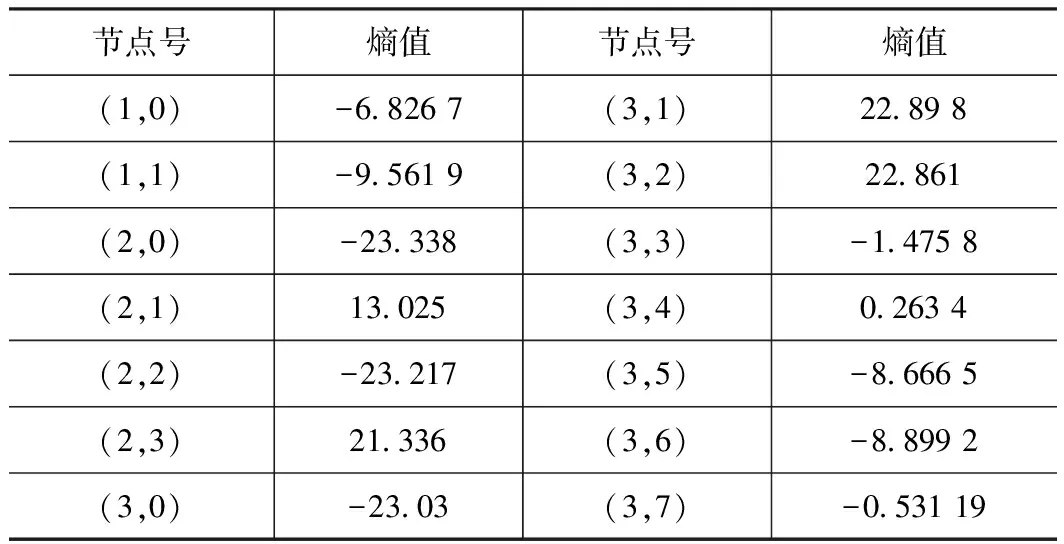
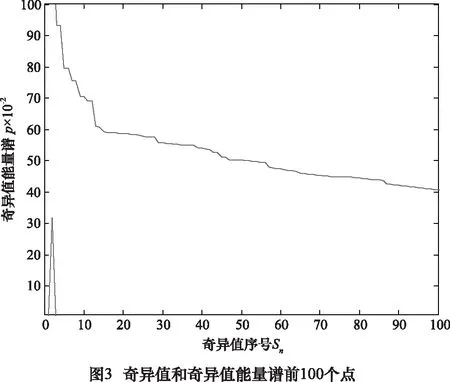
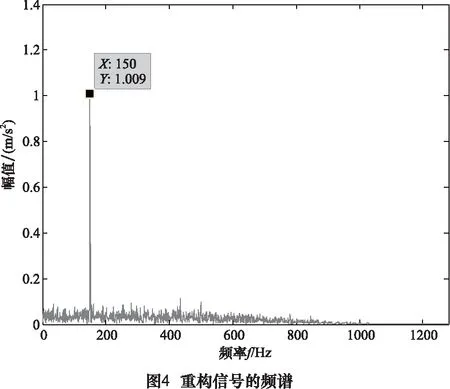
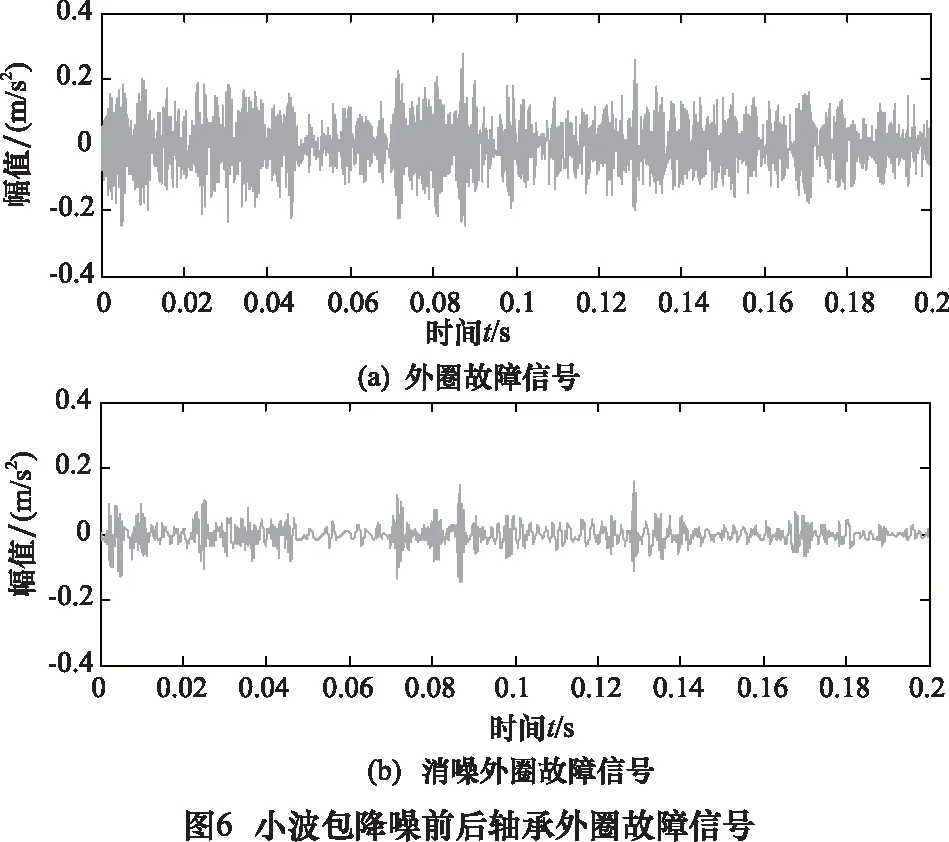
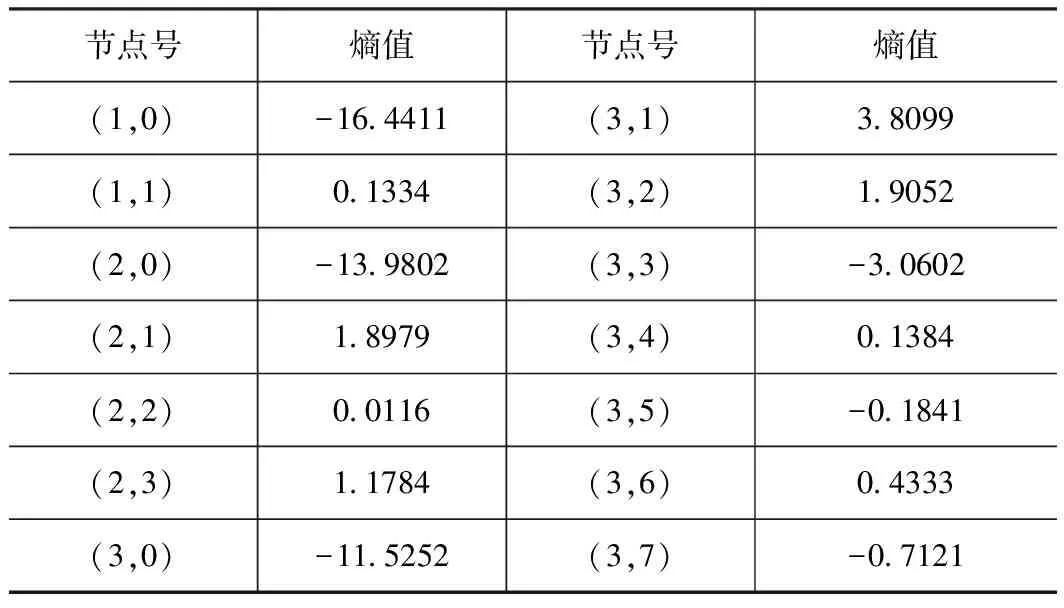
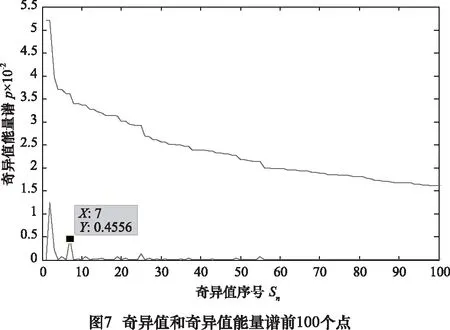
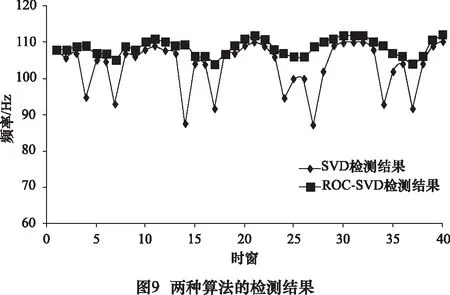
式(1)中n的范围是1 奇异值分解的本质就是实矩阵A[6-8],存在两个矩阵U=(u1,u2,…,um)∈Rm×m和V=(v1,v2,…,vn)∈Rn×n,满足公式: A=UDVT (2) 这种情况。式中的矩阵D=(diag(δ1,δ2,…,δq),0)或其转置矩阵DT,由m 此时的Hankel矩阵为最佳矩阵。 为了实现自动判断有效奇异值的个数,定义奇异值能量,并且进行能量归一处理:设所有奇异值按从小到大顺序所形成的一个序列S=[e1,e2,…,eq],则 (3) 其能量公式为 则: (4) ROC曲线即受试者工作特征曲线(receiver operator characteristic curve, ROC曲线)[5-6],最初用于评价雷达性能,又称为接收者操作特性曲线。ROC曲线是根据一系列不同的二分类方式(分界值或决定阈),以真阳性率(灵敏度)为纵坐标,假阳性率(特异度)为横坐标绘制的曲线。 传统的诊断试验评价方法有一个共同的特点,必须将试验结果分为两类,再进行统计分析[7-9]。ROC曲线的评价方法与传统的评价方法不同,无须此限制,而是根据实际情况,允许有中间状态,可以把试验结果划分为多个有序分类,如正常、大致正常、可疑、大致异常和异常5个等级再进行统计分析。因此,ROC曲线评价方法适用的范围更为广泛。 该方法简单、直观,通过图示可观察分析方法的临床准确性,并可用肉眼作出判断。ROC曲线将灵敏度与特异性以图示方法结合在一起,可准确反映某分析方法特异性和敏感性的关系,是试验准确性的综合代表。ROC曲线不固定分类界值,允许中间状态存在,利于使用者结合专业知识,权衡漏诊与误诊的影响,选择一更佳截断点作为诊断参考值。提供不同试验之间在共同标尺下的直观的比较,ROC曲线越凸越近左上角表明其诊断价值越大,利于不同指标间的比较。曲线下面积可评价诊断准确性。 在进行实时检测时,必须设定一定长度的时窗,时窗大小跟信号采集设备的采样频率有关。根据数理统计相关知识可知:50个样本以上算是大样本数据,大样本数据具有统计分布规律。因此,时窗长度与采样频率存在如下关系: (5) 式中:f为采样频率。 针对滚动轴承故障存在冲击特征非平稳、微弱等特点,本文首先运用小波包分解方法对采集到的信号进行分解得出最小熵,从而获得低信噪比的故障信息,分离出强烈的噪声,剔除干扰噪声;然后利用奇异值能量分析方法对高信噪比故障信号进行再去噪,进一步剔除伪信号,进而得到故障特征频率。具体执行步骤可分为如下: (1) 确定原始信号小波包基与分解层数,并对其进行小波分解;计算得到相应节点系数的熵值,通过比较确定出最佳的小波包基,通过信号重构得到降噪后的信号。 (2)对降噪重构后的信号构建奇异值hankel矩阵,计算奇异值序列并进行能量归一化处理,通过Hilbert变换,得到当前时窗下故障频率;再对下一时窗信号进行检测时,将上一时窗奇异值阈值作为初值,利用ROC曲线对阈值进行修正,使得相邻两时窗故障频率误差在5%以内。 (3)信号重构并进行包络谱分析,提取故障信息。 图1所示为分析流程图。ROC的具体优化过程如下: 设k时刻所检测出的故障频率为:f(k-1),奇异值阈值为s(k-1),以k-1时刻的奇异值阈值作为k时刻阈值时,检测出的故障频率为f(k),k时刻的奇异值阈值的值域为[s(k-1),smax(k)],分类标记为ST,如果|F(k)-F(k-1)|/F(k-1)≤0.05,就以此值域中的数值作为阈值,来判定一段时窗内检测出的频率是否小于0.05,若小于0.05则分类标记记为1,否则置为0,由此将分类准确率作为选择阈值的依据,最终确定每个时窗的最佳阈值。 为考察小波包最小熵与奇异值能量对轴承故障信号处理的有效性与正确性,取含有实际故障特征的仿真信号y(t)(如图2a)进行3层小波包分解,得到各个小波包节点系数,对每个节点求其熵值(如表1)并进行比较,得到最佳小波包树,如图2。阈值降噪,y′(t)。仿真信号y(t)为: y(t)=sin(2×π×150×t)+randn(t) (6) 从图2b中可知,通过降噪,信号的波动性得到一定的抑制,但依然无法得到想要的结果。 在降噪信号基础上,对y′(t)进行奇异值能量处理。首先构建相应的对角矩阵,通过奇异值分解得到信号的奇异值序列,再进行奇异值能量谱计算,奇异值能量谱中峰值位于信号前端部分,后端的峰值都趋于零。为了更有效地观察奇异值能量谱的分布情况,分别把奇异值序列前100个点的曲线图(图3中上部的第一条曲线)和能量谱(图3中下部的第二条曲线)前100个点的曲线图绘制到同一个坐标系下,如图3所示。观察图可以发现:根据初选阈值选取保留前2个奇异值后面奇异值为0,然后对奇异值重构,再进行Hilbert变换,其包络谱分析信号如图4所示。从图中清楚的找到频率150 Hz。 表1 节点熵值 节点号熵值节点号熵值(1,0)-68267(3,1)22898(1,1)-95619(3,2)22861(2,0)-23338(3,3)-14758(2,1)13025(3,4)02634(2,2)-23217(3,5)-86665(2,3)21336(3,6)-88992(3,0)-2303(3,7)-053119 实验采用加速度振动测试系统来获得机械轴承故障振动信号,并利用最小熵降噪与奇异值能量分析对振动数据提取轴承故障特征。实验台主要由电动机、转子、加载器及轴承组成。轴承为N205EM圆柱滚子轴承,其外圈故障尺寸为滚道上宽0.1 mm、深0.2 mm平行轴承轴线方向的微小沟槽,如图5,轴承内圈完整无缺。轴承内径25 mm,外径52 mm,宽度15 mm,滚动体直径为7.5 mm,节圆直径为39 mm,滚动体个数为12,接触角为0°。实验中,外圈固定,内圈旋转,使用采样频率为10 240 Hz的数据采集卡与加速度传感器对轴承转速在1 350 r/min作为分析数据对象,计算轴承各部件故障特征频率,其结果如表2所示。 表2 轴承各部件故障频率 部件名称内圈故障滚动体故障外圈故障故障特征频率/Hz16065113410935 依据图1的步骤,先对振动信号(图6a)进行小波包分解层数的确定,在轴承故障不清楚的情况下,利用公式: Jf (7) 将采集频率FSample=10 240和表2中的外圈理论故障特征频率Ffault代入公式(7),通过计算:Jf≤3.96,小波包分解层数为整数,只能取最小值Jf=3,通常绝大多数滚动轴承的故障分解层数在3~5层。 试验中确定的时窗长度为0.004 8 s,选取一段连续的数据为分析对象,利用ROC-SVD算法对故障信号进行检测;前一时刻检测出的故障频率为108.8 Hz,奇异值阈值为0.246 2。 首先结合计算结果,在此采用三层小波包分解,求小波包每个节点香农熵值并对各值比较,见表3,寻找出最小熵来构建最佳小波包树;对最小熵各节点阈值降噪并进行重构得到如图6b降噪信号,通过与原信号图(图6a)比较,可以看出:对噪声的降噪效果很明显,但故障特征依然无法确定。 表3 节点熵值 节点号熵值节点号熵值(1,0)-164411(3,1)38099(1,1)01334(3,2)19052(2,0)-139802(3,3)-30602(2,1)18979(3,4)01384(2,2)00116(3,5)-01841(2,3)11784(3,6)04333(3,0)-115252(3,7)-07121 接着运用奇异值能量分析方法对降噪重构后信号进行处理。首先对信号进行对角矩阵构建,也就是hankel矩阵构造,通过奇异值分解可以得到信号的奇异值序列,再进行奇异值能量谱计算,奇异值能量谱中峰值位于信号前端部分,后端的峰值都趋于零。为了更有效地观察奇异值能量谱的分布情况,分别把奇异值序列前100个点的曲线图和能量谱前100个点的曲线图绘制到同一个坐标系下,如图7所示。重构后的信号频谱如图8所示。 根据上一时刻确定的阈值,选取前55个点,检测出故障频率为102.1 Hz,相邻两时刻检测出的频率差值大于0.05,故需用ROC曲线对所选阈值进行优化。前55个点的奇异值值域范围为[0.2642,1.6420],对奇异值的范围进行分类,依次以值域内每一个数值为阈值,确定奇异值个数,而后通过重构与Hilbert变换得到相应的检测频率。图9是两种算法实时检测的结果。 从图9可以看出,单纯的SVD检测算法实时检测的效果并不理想,相邻时窗检测出的结果存在一定的差异性;而ROC-SVD的检测结果的一致性较好,跟实际的检测结果较为接近,且最大误差尚未超过5%。 (1)在低信噪比情况下,小波分解无法准确进行信噪分离。 (2)给出了实时在线检测的时窗确定方法。 (3)ROC-SVD实时检测结果一致性明显优于单纯的SVD算法。 [1] 王立臣,梁浩.滚动轴承故障诊断技术现状及发展趋势 [J].电子测试, 2013,22:141-143. [2] Kakarala R, Ogunbona P 0.Signal analysis using a multiresolution form of the singular value decomposition [J].IEEE Transactions on Image Processing, 2001, 10 (5): 724-735. [3]张超,陈建军,郭迅.基于EMD能量熵和支持向量机的齿轮故障诊断方法[J].振动与冲击,2010,29 (10) :216 -220. [4] 赵志宏,杨绍普.于双树复小波包变换和SVM的滚动轴承故障诊断方法[J].振动与冲击,2012,31(6):136-140,154. [5] 涂福泉,陈奎生,陈建勋,等.ROC分析技术的研究现状和发展趋势[J].计算机与数字工程,2007,35(3):33-37. [6] 张晓龙,江川,骆名剑.ROC 分析技术在机器学习中的应用[J].计算机工程与应用,2007,43(4):243-247. [7] 邹洪侠,秦锋,程泽凯.二类分类器的ROC曲线生成算法[J].计算机技术与发展,2009,19(6):109-112. [8] 邓国荣,杨朝辉.基于R O C 曲线的边缘检测算法性能评估[J].创新科技导报,2011(19):128-129. [9] 韦修喜,周永权.基于ROC曲线的两类分类问题性能评估方法[J].计算机技术与发展,2010,20(11):47-50.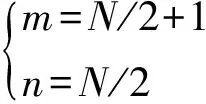

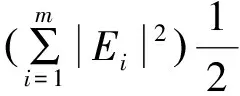
1.2 ROC曲线
2 奇异值能量与ROC曲线优化的滚动轴承故障诊断方法
2.1 时窗确定
2.2 ROC-SVD故障检测算法
3 数字仿真信号分析


4 轴承实验数据分析



5 结语
