基于经济分析的机床产品可靠性控制技术研究*

王 扬 朱 清 李 丽 钟德明 张根保

(①重庆大学机械工程学院，重庆 400044；②四川华都核设备制造有限公司，四川 都江堰 611830；③北京机床研究所，北京 100102)

1 可靠性控制的相关概念

当前，机床企业在产品生产过程中的可靠性控制主要存在如下问题：(1)往往在产品可靠性劣化到不可接受的程度之后才进行被动的控制，由于产品故障产生损失较小的情况不能进行有效分析。(2)可靠性改进的程度分析以及改进措施重要性顺序的确定还缺乏有效方法。产品可靠性提升究竟能产生多大的效益？可靠性改进到什么程度才能使得产生的效益最大化？这些企业最关心的问题还没有得到解决。(3)不同用户对产品可靠性的要求是不一样的，如何通过可靠性控制使得产品在成本不变的情况下尽可能多地满足用户群体是需要进一步研究的内容。针对这些问题，本文提出了一种新的机床产品可靠性控制方法，其流程如图1所示。

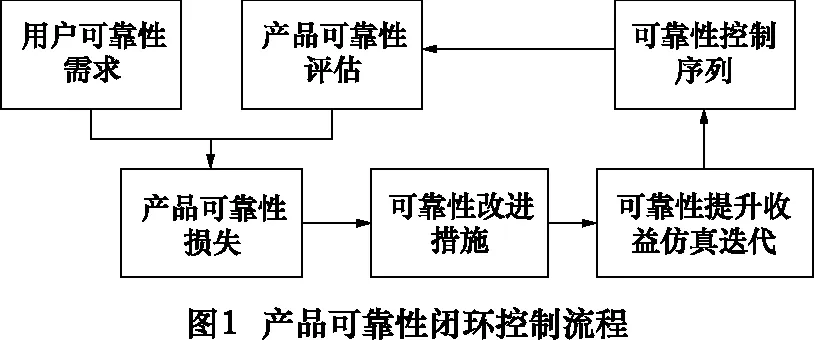
该流程首先通过收集用户对产品可靠性的需求，从而得到产品可靠性控制的目标。另一方面，利用试验数据、售后数据、用户使用数据以及产品检验数据对产品的可靠性进行评估，为分析产品故障产生的损失提供数据支撑。在充分了解产品可靠性损失的基础上，枚举出所有可选的可靠性改进措施，建立可靠性提升收益模型，对各项措施能够产生的收益进行仿真迭代，计算出最佳的可靠性控制序列。可靠性控制序列实施后，产品可靠性发生变化，则再按照此循环进行闭环控制，实现产品可靠性的有序稳定提升。

2 用户可靠性需求建模

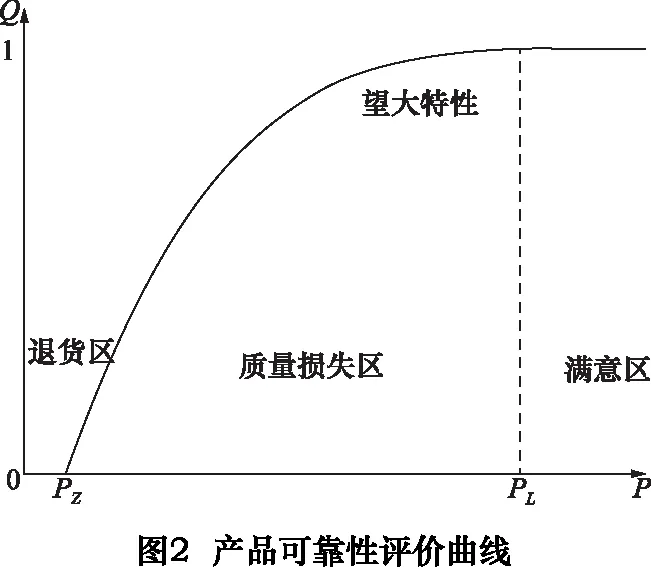
机床作为装备制造业的“工作母机”，用户在使用过程中需要机床尽可能连续不断地运行，因此，对于机床产品的可靠性要求普遍较高。平均无故障工作时间(mean time between failure MTBF)是评价机床产品可靠性最常用的指标，该指标属于望大特性，即该指标越大越好。用户对于机床平均无故障工作时间需求的差异主要体现在退货值和满意值的选取上，如图2所示。

图中，PL为满意值，当平均无故障工作时间高于此无损失值时，参数符合度Q=1，即用户对于产品可靠性达到期望。当平均无故障工作时间低于PL时，产品可靠性差会给用户带来损失，低于退货值PZ时，产品不被用户所接收。另一方面，不同的用户对于退货值和满意值的期望也是不同的。例如，A企业对于退货值的期望为700 h，而B企业由于在生产线中使用机床，对于机床可靠性的要求很高，期望值为1 200 h。这种差异可以通过分布的方式得到体现，图3给出了一个例子。

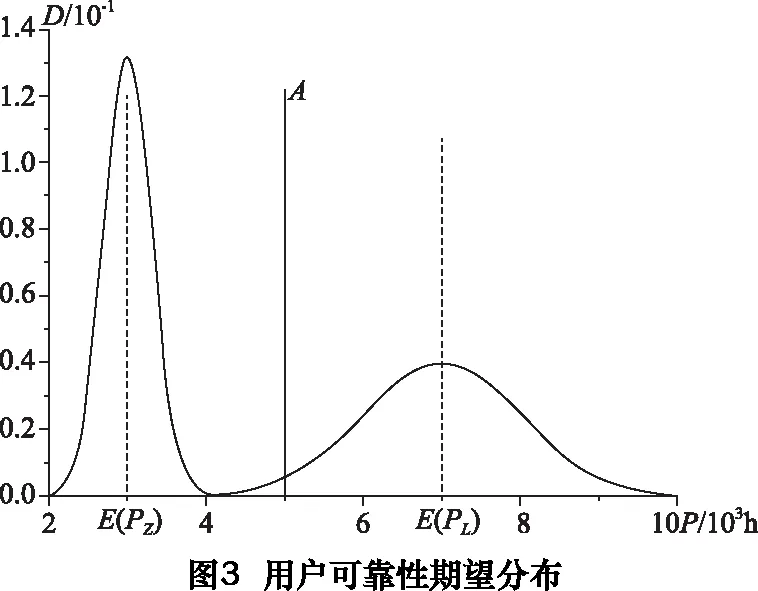
图中，P代表平均无故障工作时间，D代表用户分布的比例，左边为退货值的分布，右边为满意值的分布，样本数量一般在20以上。退货值PZ的均值为3 000 h，满意值PL均值为7 000 h，用户对于这两个值的选取都分布在期望的两边。A为假定的产品实际平均无故障工作时间值5 000 h，从而可以看出当前产品可靠性存在损失，不能满足绝大部分用户的需求。对于图中的情况，尽管A点至分布中心的数值距离是相等的，即A到的PZ的距离为3 000 h，到PL的距离也为3 000 h，但是，由于退货值的分布集中，满意值的分布较为分散，因此，产品更加趋向于可靠性损失，退货的比例极少。从图中也可以看出很少的用户认为A点处于需要退货状态。为了描述这种因为用户期望的集中程度产生的评价差异，马氏距离被引入到建模当中，从而消除分布方差带来的影响。马氏距离 (mahalanobis distance)表示数据的协方差距离。

(1)

马氏距离与变量的量纲和尺度无关，由标准化数据和中心化数据(即原始数据与均值之差)计算出的二点之间的马氏距离相同。这些优点使得它非常适合用来对产品可靠性特性进行评价。此处，DM为马氏距离，x为无故障工作时间，μ为用户期望的样本均值。

3 产品可靠性损失计算

产品的平均无故障工作时间记为X，存在用户可接受的最小平均无故障工作时间(退货值)PZ和损失产生的临界平均无故障工作时间(满意值)PL。用户对于产品平均无故障工作时间(MTBF)的直观认识在于产品使用过程中的故障数。在某一给定时间段T内，实际产生的故障数N与用户期望的可靠性无损失故障数N0之间的偏差为：

(2)

当平均无故障工作时间达到用户可接受的最小平均无故障工作时间时，故障数偏差达到最大：

(3)

根据用户期望符合度函数的定义，在临界可靠性损失PL处的可靠性损失期望为0，可靠性损失零点PZL处的可靠性损失期望为1。因此，建立的可靠性损失函数为：

(4)

该可靠性损失函数建立在用户期望符合度的衰减过程是随着故障数与预期的偏差增大线性递减的。平均无故障工作时间X，在本文中被认为符合威布尔分布，其概率密度函数为：

(5)

式中：k、λ分别是分布的形状参数、尺度参数。通过采用定时截尾方法对机床进行试验及已经出厂机床产品售后所收集的数据进行分析，利用软件拟合威布尔分布进行分布检验和参数估计。可靠性损失函数中相减的部分以马氏距离的平均值进行计算，其余部分以期望进行计算。即：

(6)

此处，平均距离函数的第一个参数PL为计算中心距离的目标分布。

4 机床产品可靠性评估

机床产品可靠性评估的关键在于故障数据的收集和统计分析，产品的故障间隔时间服从威布尔分布。本节中，某企业对该厂MKS16系列数控磨床进行可靠性综合评价，并根据评价结果进行相应的可靠性提升。机床可靠性评价通过收集试验故障数据以及售后故障数据，进行故障分析。利用威布尔分布检验并拟合故障数据，得到无故障工作时间分布X。将148个故障间隔时间数据t∈[0，265 6]分为14组，绘制统计直方图并拟合威布尔分布曲线，如图4所示。

拟合结果，形状参数k=0.881 46，尺度参数λ=499.691 78。利用Matlab在显著性水平5%条件下对该结果进行检验，检验结果为：H=0，P=0.565 4，测试统计量的值ksstat=0.064 0小于临界值cv=0.111 2，表明不拒绝该假设。同理，对用户期望进行调研，利用正态分布进行拟合，得到PL和PZL的分布。参数及检验水平为0.05的t检验结果如表1所示。

表1 用户期望PL和PZL的分布参数

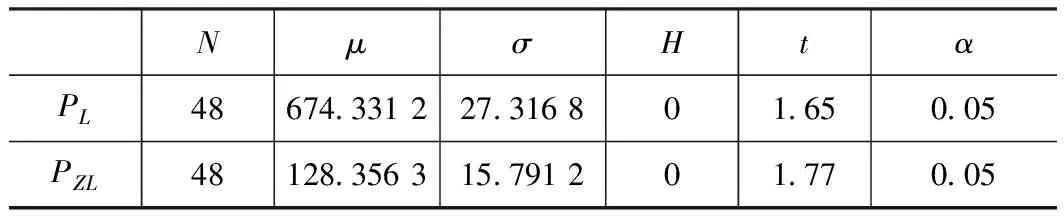
NμσHtαPL4867433122731680165005PZL4812835631579120177005

5 可靠性改进措施

机床的可靠性改进措施主要通过故障树分析(fault tree analysis FTA)来确定。砂轮架子系统作为数控磨床关键功能部件，其工作性能好坏直接影响所加工工件质量高低。因此以MKS1632型号的数控外圆磨床的砂轮架子系统为研究案例，来阐述具体的可靠性改进措施。通过对砂轮架系统的典型早期故障进行FTA分析可得图5～7故障树。

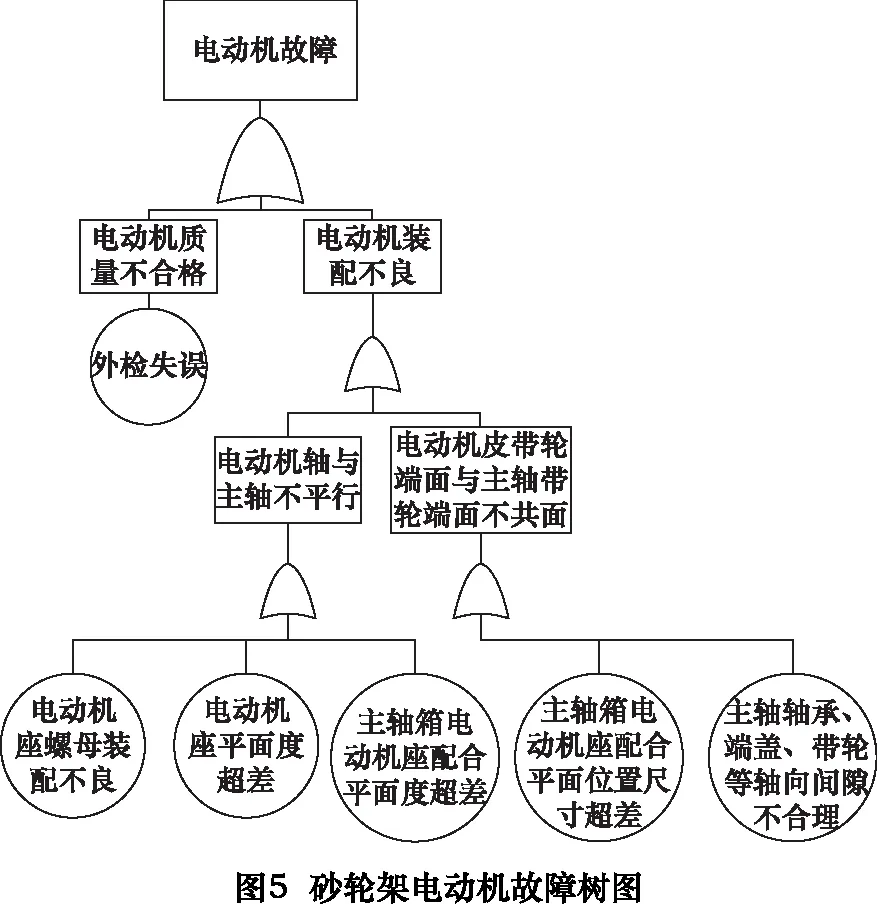
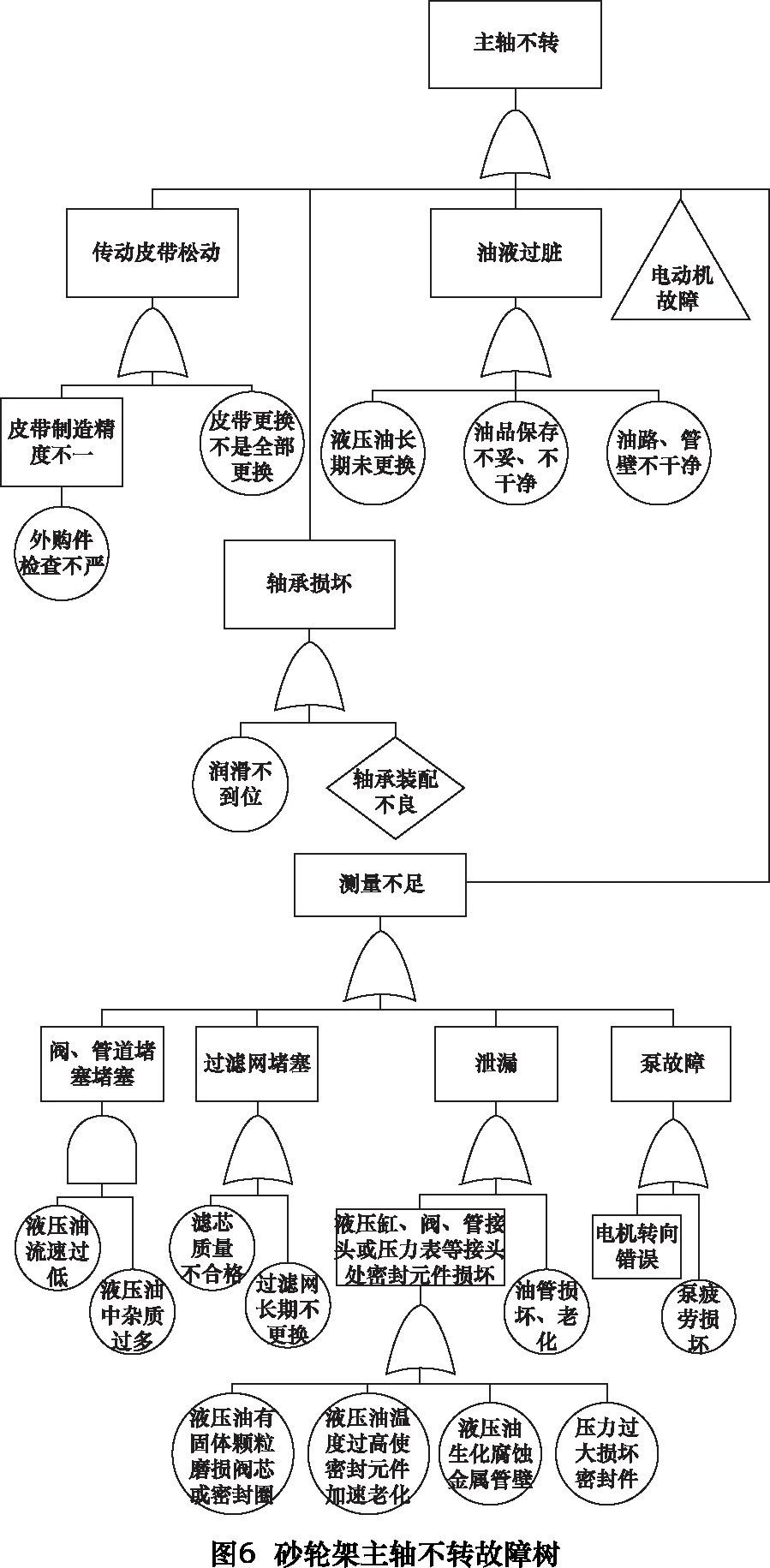
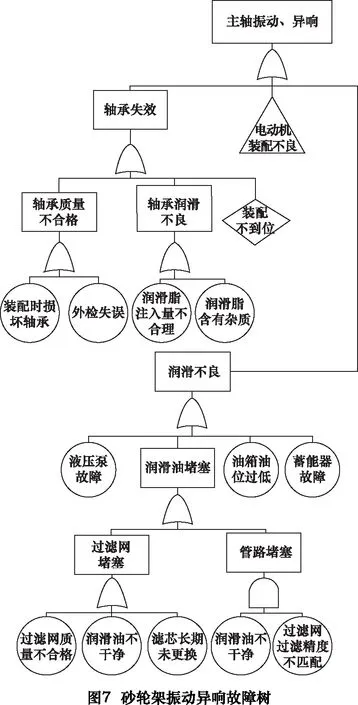
根据图5～7故障树分析，可以得到如下结论：

(1)主轴部分为故障常发生部位，主要原因有润滑油不干净，长期未更换。在使用过程中应该定期维护、清洗油路、更换主轴油。

(2)电动机安装过程应当注意紧固螺栓的拧紧力，装配完要进行试运行，排除造成电动机震动的原因。

(3)传动皮带作为外购件，需要对供应商进行考核评估，确保皮带精度及制造一致性。在入场检验时需对皮带松紧度进行试验考评。需要更换皮带时最好一次性全部更换。

消除砂轮架故障的详细措施见表2所示。

6 可靠性提升效益仿真迭代

表2 砂轮架故障消除措施

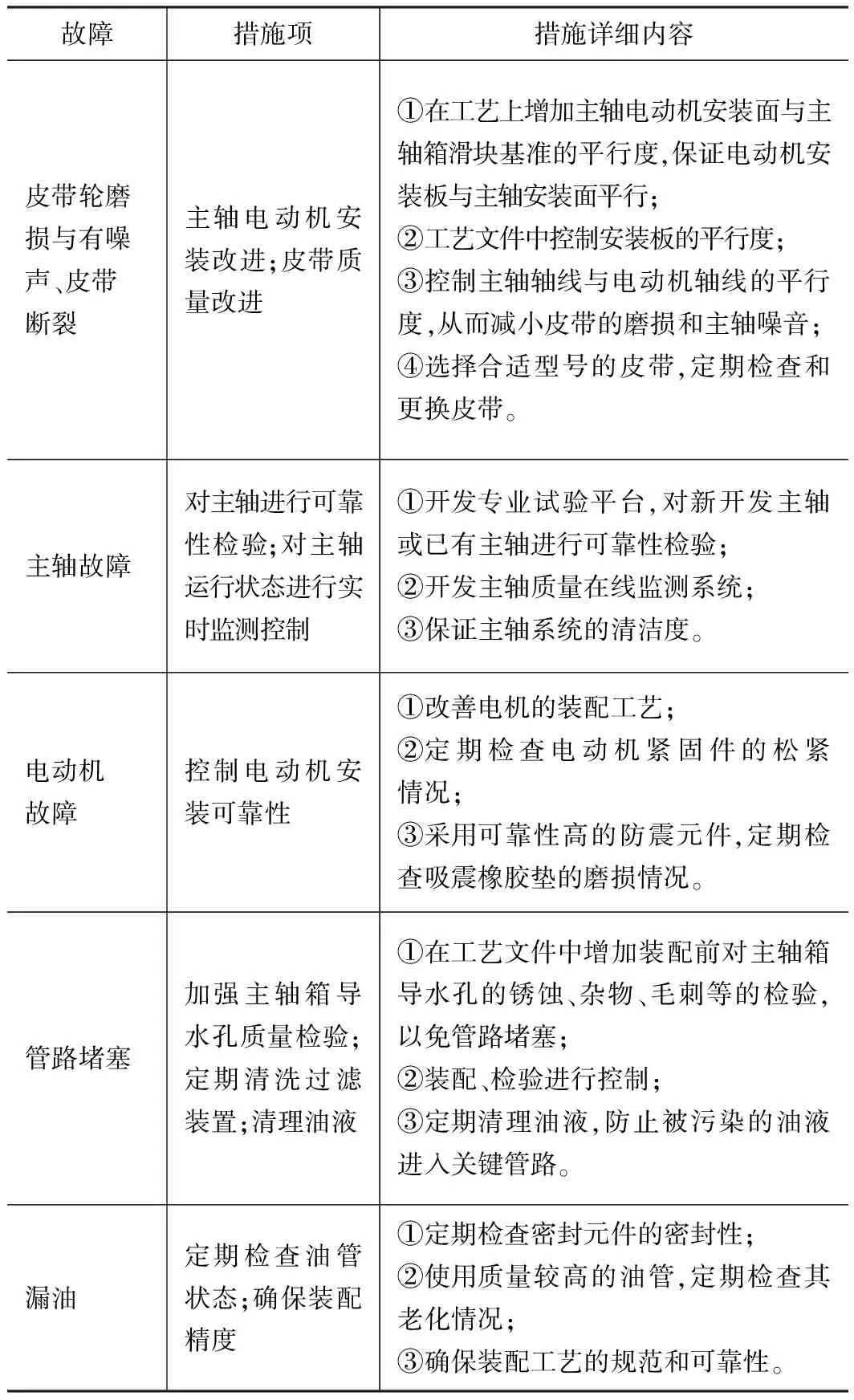
故障措施项措施详细内容皮带轮磨损与有噪声、皮带断裂主轴电动机安装改进；皮带质量改进①在工艺上增加主轴电动机安装面与主轴箱滑块基准的平行度，保证电动机安装板与主轴安装面平行；②工艺文件中控制安装板的平行度；③控制主轴轴线与电动机轴线的平行度，从而减小皮带的磨损和主轴噪音；④选择合适型号的皮带，定期检查和更换皮带。主轴故障对主轴进行可靠性检验；对主轴运行状态进行实时监测控制①开发专业试验平台，对新开发主轴或已有主轴进行可靠性检验；②开发主轴质量在线监测系统；③保证主轴系统的清洁度。电动机故障控制电动机安装可靠性①改善电机的装配工艺；②定期检查电动机紧固件的松紧情况；③采用可靠性高的防震元件，定期检查吸震橡胶垫的磨损情况。管路堵塞加强主轴箱导水孔质量检验；定期清洗过滤装置；清理油液①在工艺文件中增加装配前对主轴箱导水孔的锈蚀、杂物、毛刺等的检验，以免管路堵塞；②装配、检验进行控制；③定期清理油液，防止被污染的油液进入关键管路。漏油定期检查油管状态；确保装配精度①定期检查密封元件的密封性；②使用质量较高的油管，定期检查其老化情况；③确保装配工艺的规范和可靠性。

传统的机电系统可靠性的效益和费用分析主要集中在敏感性分析。当前，机电系统的复杂程度越来越高，这些方法的局限性逐渐暴露出来，各种参数间的耦合因素以及多因素的变动使得传统建模无法适用于现有的机电系统。因此，区间分析方法被提出，用来对多种不确定性因素下的可靠性经济指标进行定量求解。本文将美国电气和电子工程师协会(IEEE)所推荐的可靠性经济性模型岁收需量法与区间分析方法相结合，建立了机电系统可靠性经济特性模型，并通过仿真模拟对模型进行了验证。岁收需量法的基本公式为：

G=X+f·C

(7)

式中：G为制造企业在投产还贷期最小年收入；X为变动成本；C为可靠性项目投资；f为最小投资回报系数，反映因资金成本、折旧方式、还款时间、工程建设期等资金运作方式对于成本的影响。变动成本X可以表达为：

X=λ[xi+(gp-xp)(r+s)]X=λ[xi+(gp-xp)(r+s)]

(8)

式中：λ是每年的故障数或者故障率；xi是每个故障产生的额外费用，元/故障；gp是用户企业每小时停工产生的费用，元/h，xp是用户企业每小时停工节省的费用，元/h；r是设备故障后维修或者替换的时间，h；s是维修后再投入生产的时间，h。部件失效所产生的后果引起可变费用的增加。费用增加的程度由故障在系统中的部位以及分布类型有关，设备本身的质量以及安装质量对于故障数有很大的影响。当故障发生时，故障本身会产生费用，另一部分费用的增加正比于设备处于故障的时间。最小投资回报系数f包含如下几个部分：最小的可接受的投资回报率，包括风险；所得税；设备折旧；固定费用。计算投资回报系数的表达式为：

(9)

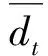
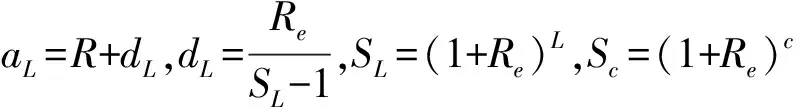
(10)

式中：dL为偿债基金因子。每一个不同的备选方案都对应不同的投资，以计算出各方案的总投资费用作为选择的条件，也可以计算一个最小的底限投资下各方案的增加费用进行判别。由于最小投资回报系数的存在，计算费用增加的方法存在一定的误差。

区间分析方法将定义在实数域R上的所有区间数的集合记为I(R)，区间数和区间函数通过方括号与普通的实数和函数加以区分。区间数的上下端点一致时，区间退化为点值。区间函数所有的参数变为点值时，函数退化为点值公式。

设g:Rn→R，如果存在区间映射[G]:I(Rn)→I(R)对任意的xi∈[X]i，(i=1,2,…，n)成立，[G]([x1,x1],[x2,x2],…,[xn,xn])=g(x1,x2,…,xn)，则称[G]为函数g的函数扩展。

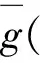
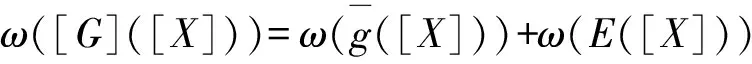
(11)

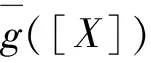
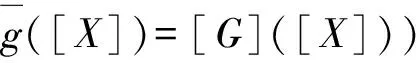
(12)

对于式(8)所给出的计算公式，函数中的参数均为区间数。表3根据企业数据，给出MKS1632型数控磨床产品的各项参数。

表3 模型参数列表

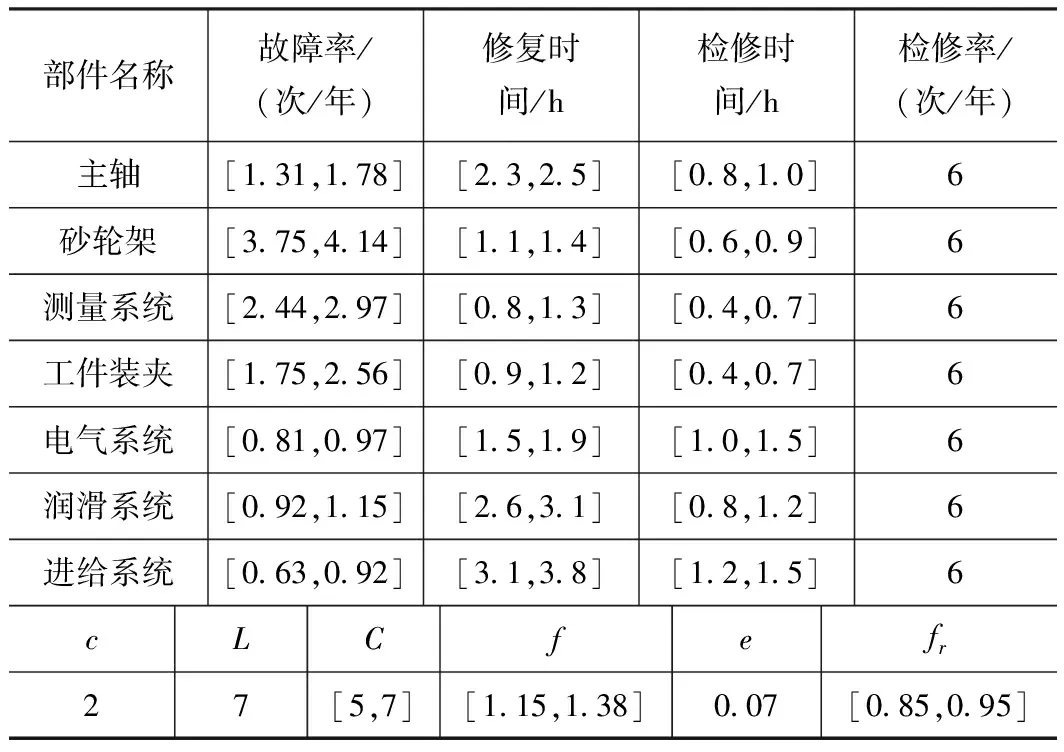
部件名称故障率/(次/年)修复时间/h检修时间/h检修率/(次/年)主轴[131，178][23，25][08，10]6砂轮架[375，414][11，14][06，09]6测量系统[244，297][08，13][04，07]6工件装夹[175，256][09，12][04，07]6电气系统[081，097][15，19][10，15]6润滑系统[092，115][26，31][08，12]6进给系统[063，092][31，38][12，15]6cLCfefr27[5，7][115，138]007[085，095]

利用Matlab对所建立的区间分析模型进行仿真可得图8。

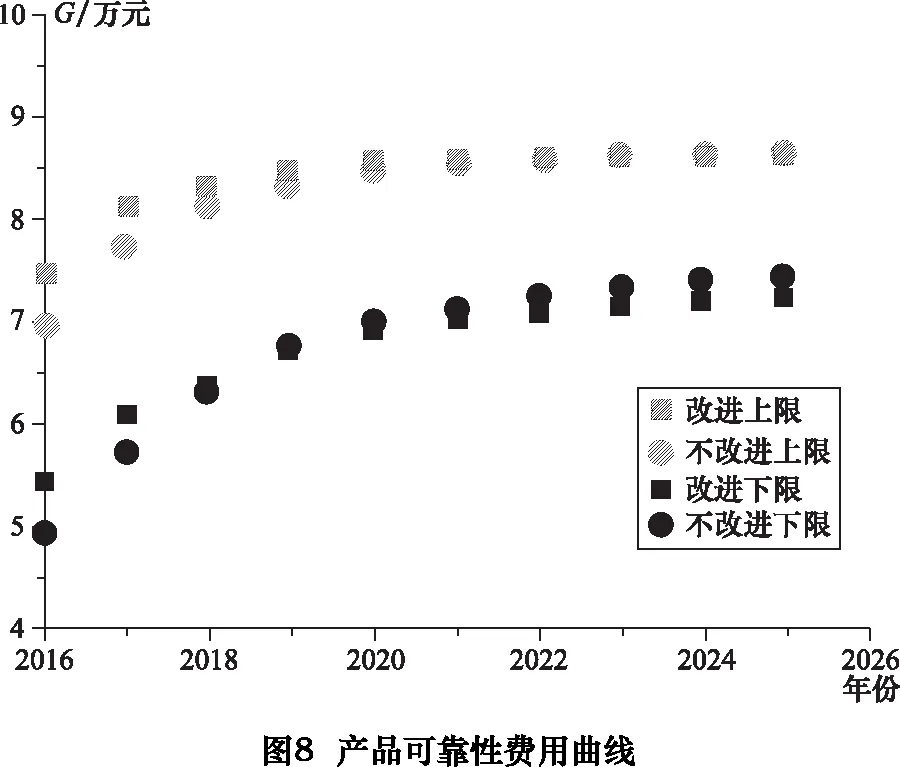
由图8所示产品可靠性费用曲线G可以看出，在产品生产的前4年里，无论是可靠性费用的上界还是可靠性费用的下界，可靠性改进过程的曲线都因为有改进成本的存在而高于未改进的曲线。而在4年后，由于可变可靠性成本的降低，两条曲线逐渐接近，直至最终改进曲线低于未改进曲线。

具体分析曲线趋势，两条曲线的接近速度也是由快变慢。这也是由于可靠性边际效用和边际成本的变化规律所决定的。可靠性改进开始时，大量容易解决的故障被消除，从而能够大幅提升产品可靠性，快速产生效益，因此，可靠性回报较大。当产品可靠性逐渐稳定时，再通过可靠性提升获得效益则较为困难。可靠性边际效用和成本曲线如表4所示。

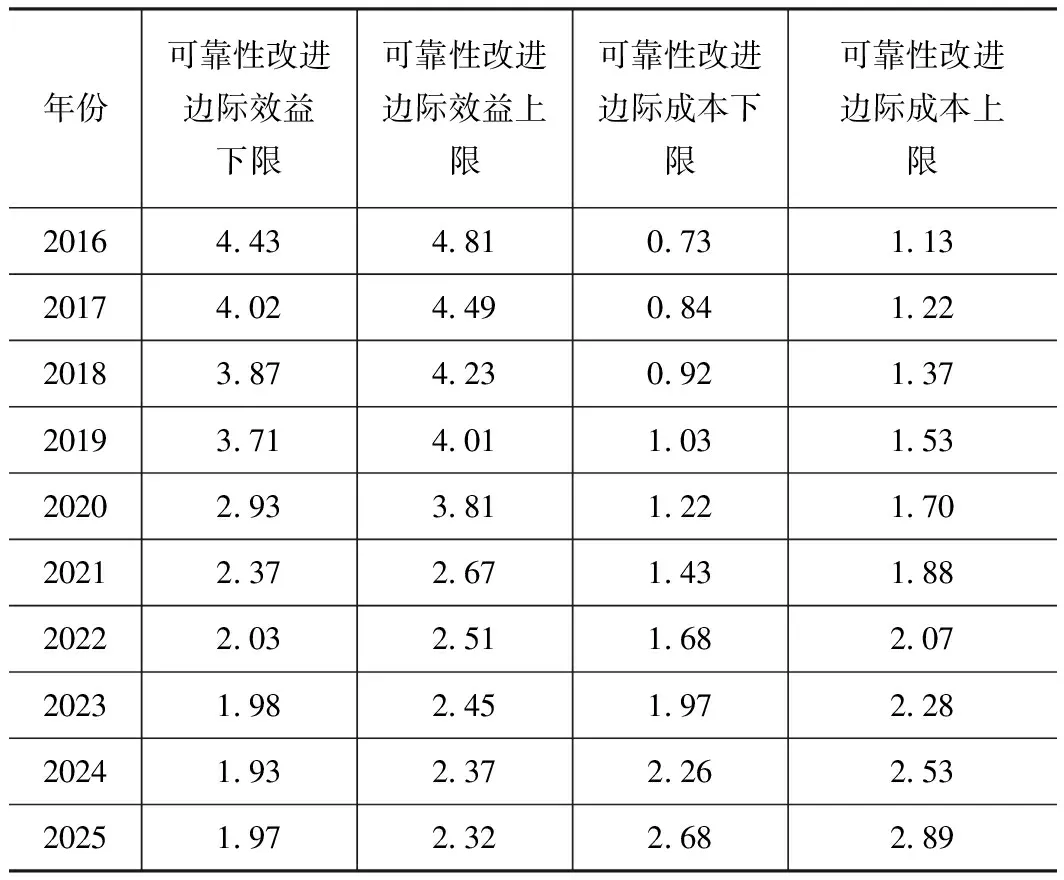
表4 可靠性改进边际成本和边际效益 万元

由可靠性改进边际成本和边际效益可知，产品在可靠性改进的初期效益明显。无论是改进效益的上界还是改进效益的下界都高于可靠性边际成本。到了2022年时，两者的差距逐渐减小，并且减小的速度也逐渐放慢。直到到了2024年，边际效益与边际成本几乎重合。这说明产品的可靠性收益与可靠性投入几乎持平，再继续采取可靠性改进措施将得不偿失。因此，应当于此时停止可靠性改进措施。

7 可靠性控制序列

本节通过计算可靠性提升措施的效费比，对各改进措施的优先程度进行评价。可靠性改进措施在本节中有如下假设：

(1)能够在一定精度和置信度范围内确定该改进措施对于平均无故障工作时间的影响。例如，更换外购件砂轮的供应商能够将额定条件下砂轮故障发生比例由10%下降到5%，同时，MTBF增加50 h。

(2)给定的可靠性改进策略下，该措施对于所有产品可靠性的影响是均一、独立的。例如，更换砂轮的供应商后，所有产品平均无故障工作时间得到的提升被认为是一致的。

(3)各改进措施对于产品可靠性的提升是相互独立的。例如，砂轮的改进措施与头架的改进措施对于产品可靠性的影响可以相互叠加。

(4)措施改进的成本是可以确定的。这一条主要针对技术、人工、改进周期等非经济投入的量化，在本节中都折算成相应的成本并且平均到每一台出厂机床。

以上假设是为了简化各可靠性提升措施对于产品可靠性特性的影响存在复杂的耦合关系的情况，该耦合关系可以通过相关性分析以及聚类分析进行解耦，在本文中不做讨论。效费比的计算以可靠性损失的减少与改进措施成本的比值进行计算：

(13)

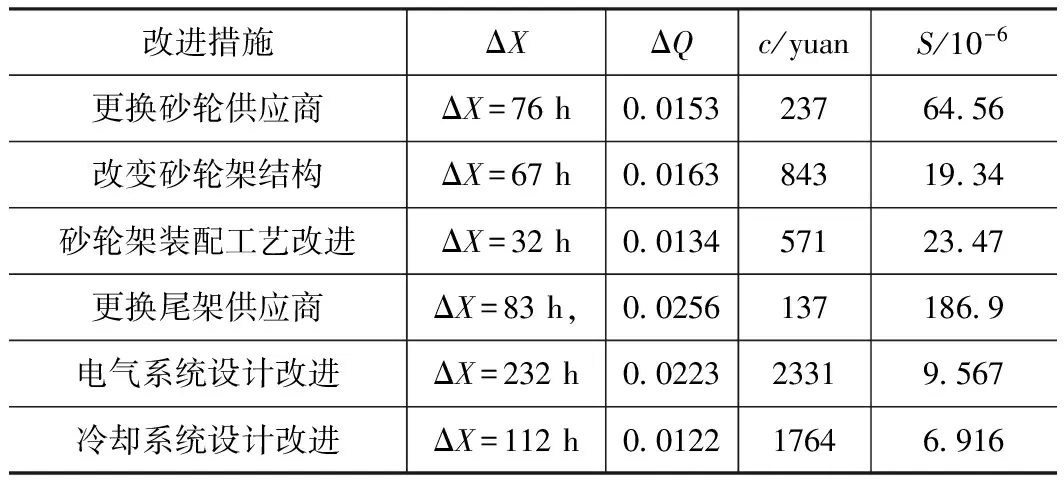
得到各可靠性提升措施的效费比计算结果如表5所示。

表5 可靠性提升措施效费比计算

改进措施ΔXΔQc/yuanS/10-6更换砂轮供应商ΔX=76h001532376456改变砂轮架结构ΔX=67h001638431934砂轮架装配工艺改进ΔX=32h001345712347更换尾架供应商ΔX=83h，002561371869电气系统设计改进ΔX=232h0022323319567冷却系统设计改进ΔX=112h0012217646916

由可靠性改进措施效费比的计算可以看出，利用可靠性参数更高的供应商提供的外购件对故障发生较多的外购件进行替换能够得到极大的效用费用比，既能够较大幅度地提升产品可靠性，又能够节约可靠性提升的成本，应该优先予以执行。而涉及到产品设计改进可靠性提升策略，虽然也能够对产品可靠性进行提升，但是平均到单台机床的成本较高，应该在产品可靠性改进循环执行到一定程度后，其他可靠性改进措施的效费比低于设计改进消费比后，再执行产品设计改进。可靠性改进措施属于动态循环过程，随着产品可靠性参数的改变而变化。

表5也说明，在产品处于可靠性水平较低的阶段时，对产品进行可靠性改进能够有很好的效果，即少量的投入能够得到非常大的回报。当产品可靠性到达一定的水平之后，再对产品可靠性进行改进，收到的效果很小，费用却很高。该项分析能够将产品可靠性改进投入所得到的效用最大化。

8 结语

本文从机床可靠性提升的目的入手，以用户需求和可靠性提升效益为优化目标，阐述了产品可靠性控制的流程。并以实例分析了流程中各环节的分析步骤，为企业提升自身产品的可靠性提供了明确的思路。结论表面，产品可靠性的提升不仅能让用户对自己的产品更加满意，还能够为企业带来直接的经济效益，同时，效费比的计算分析了合理有序的可靠性改进措施序列，从而为机床企业的可靠性提升决策提供定量的依据。

[1]张根保, 王扬, 李冬英, 等. 基于可靠运行区间重叠度的设备维修决策模型[J]. 计算机集成制造系统, 2015(3): 859-866.

[2]张根保，王扬.五轴加工机床可靠性概述[J] 金属加工：冷加工, 2015(18) :43-47.

[3]张根保，王扬.可靠性经济分析 “数控机床可靠性技术”专题(三)[J]. 制造技术与机床, 2015(9): 5-10.

[4]开宗舜．机械制造装配工艺设计与装配CAPP[M]．北京：机械工业出版社，2006.

[5]金垚, 仓婷, 潘尔顺, 等. 基于田口质量损失函数和控制图设计的经济生产批量模型[J].计算机集成制造系统，2011,7(11):2224-2230.

[6]李巧良. 可靠性工程师手册 [M]. 北京: 中国人民大学出版社，2012.

[7]张鹏, 王守相. 电力系统可靠性经济评估的区间分析方法[J]. 中国电机工程学报, 2004， 24(2) : 71-77.

[8]张根保，唐贤进，许智，等．数控机床基于状态监测的视情维修决策研究[J]．机械科学与技术，2012，31(2)：182-185.

[9]曾照辉，郭云健，焦国太.熵理论在正态分布零件模糊可靠性设计上的应用[J].煤矿机械.2010,31(1)：32-34.

[10]李进才,甘德文，梁忠权，等. 复杂机电产品关键装配工序物料质量损失评估及预警方法[J]. 计算机集成制造系统, 2014, 20(6): 1432-1442.