基于最小二乘法的电主轴回转精度评价*
2018-03-20王立平张彬彬
王立平 张彬彬 吴 军
(清华大学机械工程系,北京100084)
高速、高精度、高可靠性是当代数控机床的发展方向[1-4]。电主轴作为高档数控机床的核心部件,其回转精度直接影响机床的加工精度、性能稳定性,因此需要深入研究电主轴回转精度的测量和评定方法,分析电主轴的运动状态和判断误差产生的原因,为提高电主轴的回转精度奠定基础。根据机床检验通则第7部分:回转轴线的几何精度[5-6],评定电主轴的回转精度首先要找到电主轴高速转动下径向位移信号的最小二乘圆圆心,才能实现电主轴的回转精度评定。但基于最小二乘法的电主轴回转精度计算方法不存在解析解,因此,在面对大量数据的情况下,只能采用假设近似解或者迭代算法实现,其存在计算精度低或者计算时间长等问题。
本文以应用于五轴加工中心上的高速电主轴为研究对象,研究基于最小二乘法的电主轴回转精度评定。首先建立电主轴工作状态下的几何误差模型,对电主轴的常量信号、偏心信号等相关信号进行研究和分离。其次采用标准球、高精密电容位移传感器、高速采集卡等器件搭建电主轴回转精度测量系统,并采集电主轴高速转动下的径向位移信号。接着分别采用最小二乘牛顿迭代算法、最小二乘近似算法和平均值算法对信号进行处理与分析,并验证了3种算法的有效性。最后在分析对比3种算法结果后,设计了一种不同应用背景下的电主轴回转精度评价策略,并提出了一种兼顾计算精度和计算效率的电主轴回转精度快速评价算法。
1 电主轴几何误差建模
首先对电主轴回转几何误差进行建模,电主轴检测装置如图1所示,其原理为在电主轴前端安装标准球,并在球的两侧安装两个相互垂直的位移传感器,来采集电主轴径向运动信号。
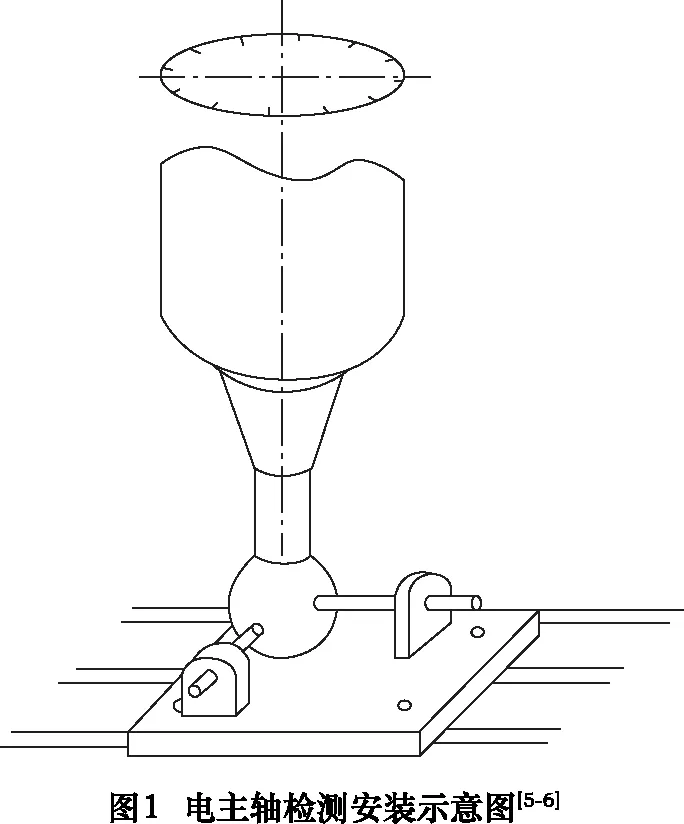
将电主轴旋转运动进行建模,并将电主轴与检测装置沿着回转中心轴方向进行投影,可得到如图2所示的原理图。图中o点表示电主轴旋转中心,O点表示标准球球心。一般来说,电主轴旋转都存在偏心现象,因此在图2中电主轴的旋转中心点o和标准球心点O不重合。以o点为原点,位移传感器1和位移传感器2检测的光线方向分别为x轴和y轴,建立坐标系o-xy。
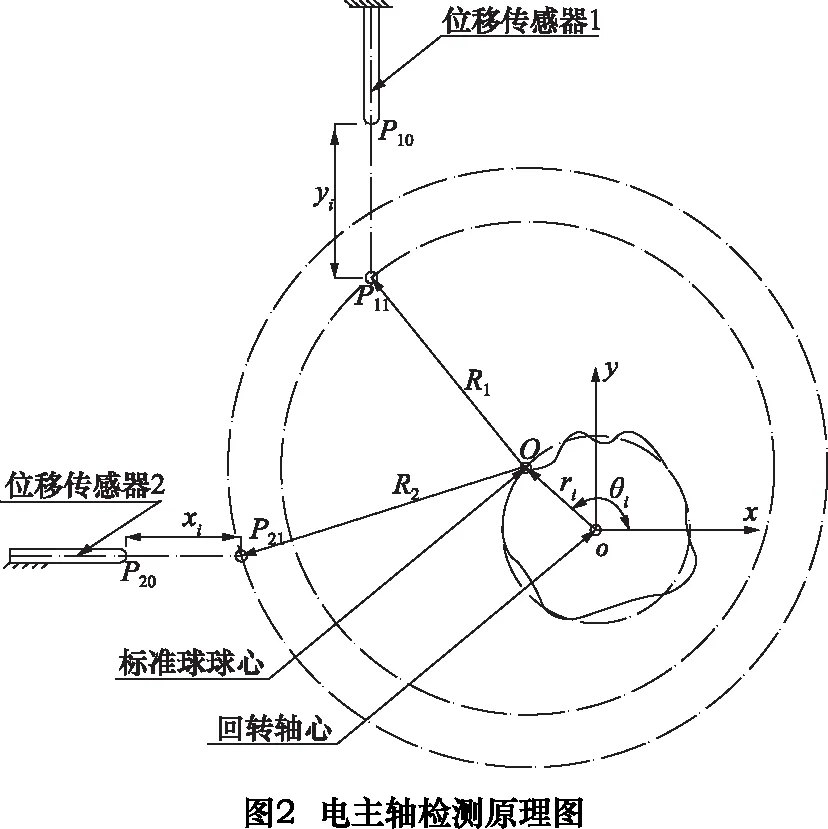
由勾股定理得到各点之间的位置关系:
yi=|P10y|-risinθi-
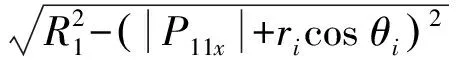
(1)
(2)
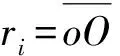
为了便于说明,设:
(3)
(4)
由式(1)~(4)得,yi是偏置信号|P10y|、正弦信号-risinθi以及余弦信号-C1i的叠加。对于高精密电主轴,|P11x|和ri基本为几十微米,检测标准球的半径R1为几厘米,即:
(5)
通过不等式分析可以得到C1i的峰峰值:
C1max-C1min≪2ri
(6)
因此,余弦信号-C1i相对于正弦信号-risinθi来说,基本上为一恒定常值,则yi可改写为:
yi=C3-risinθi
(7)
其中C3表示恒值,即:
C3=|P10y|-C1i
(8)
同理可得到:
xi=C4-ricosθi
(9)
其中C4表示恒值,即:
C4=|P20x|-C2i
(10)
通过上式,可以发现xi和yi是两个正弦信号。但由于电主轴在转动的过程中,实际转速不一定与指令转速恒等,而是一个在设定转速上下波动的变量,无法直接求解转速与旋转角度θi。因此可以转换为如下求解方式:
(11)
(12)
综合式(11)和(12)可得到主轴径向回转曲线:
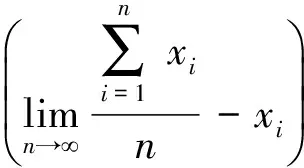
(13)
2 电主轴回转精度常用评定算法分析
参考国标,电主轴回转精度一般采用最小二乘圆评定方法进行评定,其原理图如图3所示。

最小二乘圆计算公式为:
(14)
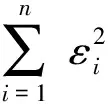
但由于最小二乘圆计算方法无解析解,若要获得精确解,一般需要采用迭代算法。下面将对最小二乘牛顿迭代算法、最小二乘近似算法和平均值算法分别展开进行分析。
2.1 最小二乘牛顿迭代算法
首先采用牛顿迭代法求解最小二乘圆。为了方便计算,不妨设:
(15)
对f(x0,y0,rlms)求偏导得到:
(16)
再对f(X)′求偏导,可得到Jacobi矩阵:
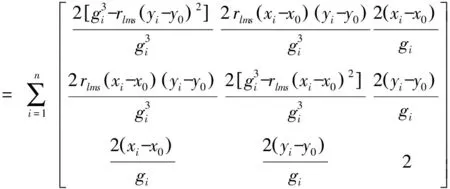
(17)
因此得到牛顿欧拉迭代函数:
X(k+1)=X(k)-[J(X(k))]-1f(X(k))
(18)
其初值设置可设置为平均值,即:
(19)
2.2 最小二乘近似算法
由于最小二乘法无法得到解析解来直接求解精度,因此可对最小二乘法进行一定的近似,采用近似函数来进行求解。该近似函数为:
(20)
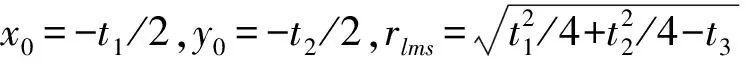
由于H的最大值是无穷大,因此当H的梯度为0时,H为最小值,即:
(21)
将t3消去后,可得到:
(22)
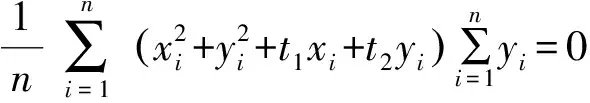
(23)
化简后可得到:
A1+A2t1+A3t2=0
(24)
A4+A3t1+A5t2=0
(25)
其中:
(26)
(27)
(28)
(29)
(30)
联立式(24)~(30)可得到:
(31)
(32)
将式(31)和(32)代入式(21)可得到:
(33)
最终得到x0、y0和rlms的近似解,即:
(34)
(35)
(36)
2.3 平均值算法
最后给定一种最常见的平均值计算方法,即直接求平均值作为最小二乘圆,即
(37)
(38)
(39)
3 电主轴回转精度信号采集与分析
电主轴回转精度检测试验台如图4所示,主轴采用博特精工的JSZD170C-12/15XJ型号电主轴,通过在主轴前端夹持一个标准球,并同时在标准球的XYZ三方向上分别放置3个高精密电容位移传感器,用于检测电主轴的径向跳动和轴向跳动。

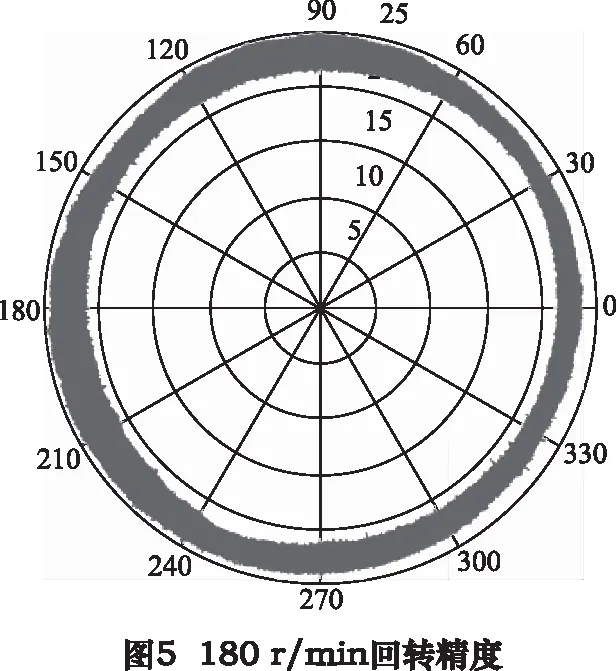
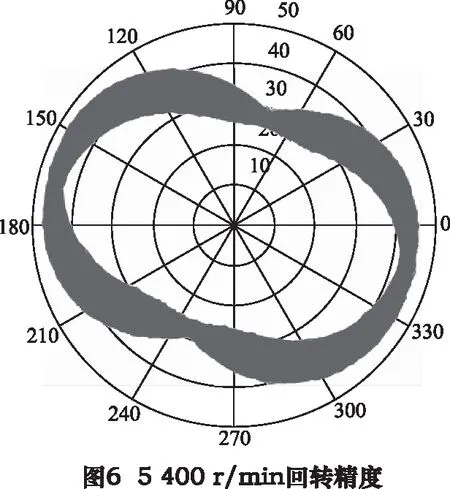
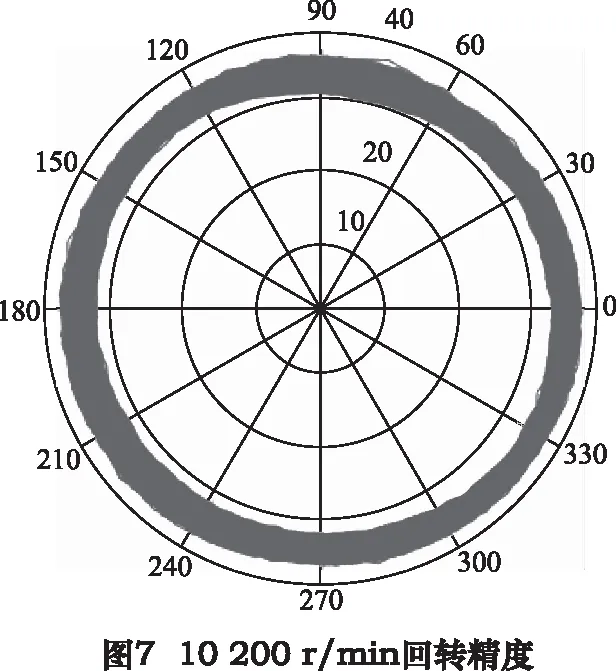
由于电主轴在低转速下,容易出现过流报警而无法转动,因此首先通过实验的方法,找到电主轴的最低转速180 r/min。接着从600 r/min转速开始,依次以600 r/min的幅值增加电主轴转速,直至达到最高转速10 200 r/min。保持每种转速下工作3 min,用NI采集卡以8 kHz的采样频率对径向位移信号进行采集,记录下18组采集数据。选取其中典型的3组信号,画出径向运动轨迹图,如图5~7所示。由图可得,主轴在低转速(180 r/min)和高转速(10 200 r/min)下,其运动轨迹是规则圆形,当处于中间转速(5 400 r/min)时,其运动轨迹发生突变。

通过对比可以发现,最小二乘牛顿迭代算法的最小二乘圆与各点的距离之和最小,即计算精度最高,但所需计算时间远大于最小二乘近似算法和平均值算法的计算时间。比对各组转速的结果后,最小二乘近似算法和平均值算法在低转速时,精度差距不大,当转速升高后,最小二乘近似算法精度高于平均值算法,与最小二乘牛顿迭代法精度差不多。
表1 3种算法计算精度和计算时间对比
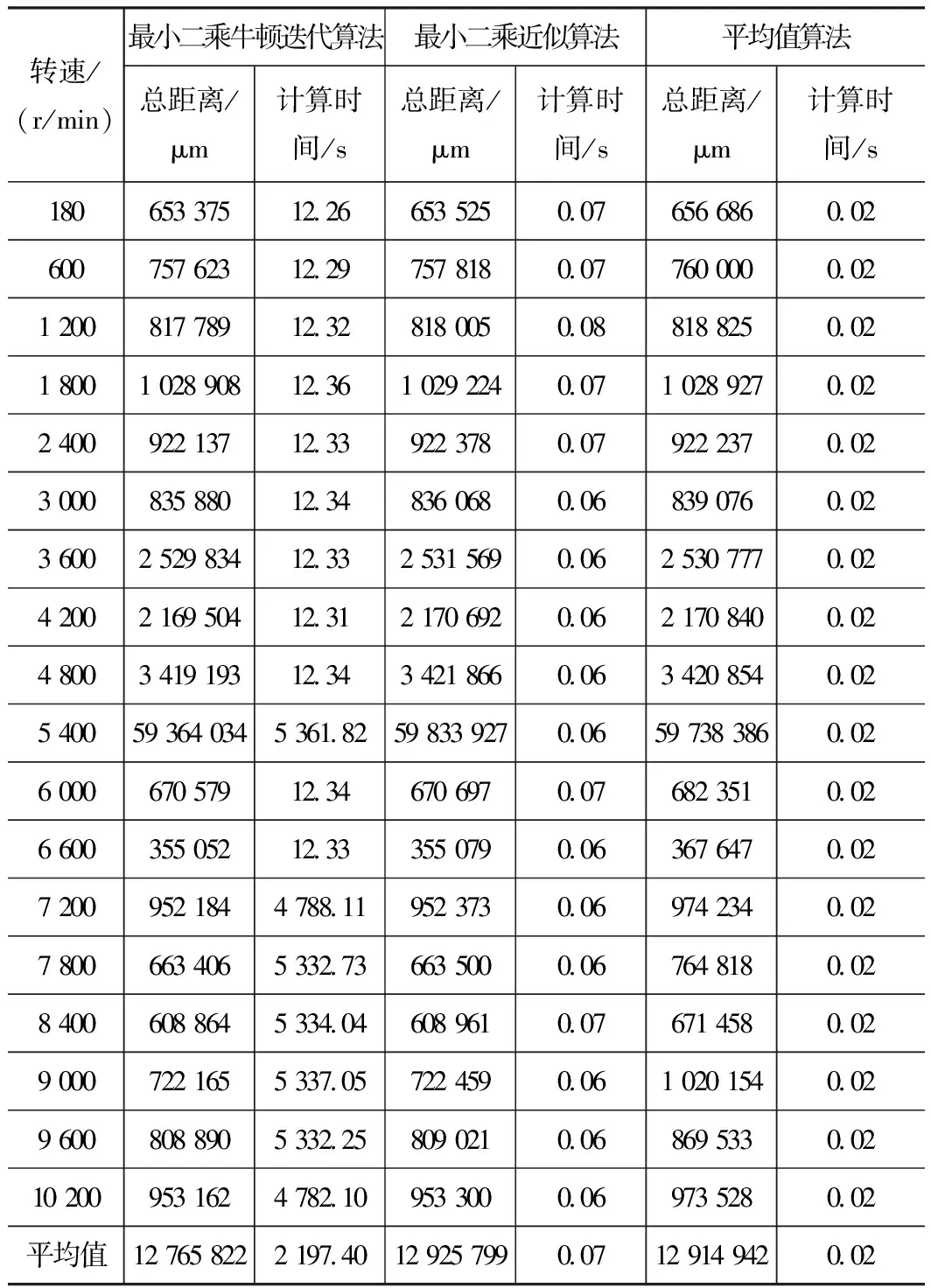
转速/(r/min)最小二乘牛顿迭代算法最小二乘近似算法平均值算法总距离/μm计算时间/s总距离/μm计算时间/s总距离/μm计算时间/s18065337512266535250076566860026007576231229757818007760000002120081778912328180050088188250021800102890812361029224007102892700224009221371233922378007922237002300083588012348360680068390760023600252983412332531569006253077700242002169504123121706920062170840002480034191931234342186600634208540025400593640345361825983392700659738386002600067057912346706970076823510026600355052123335507900636764700272009521844788119523730069742340027800663406533273663500006764818002840060886453340460896100767145800290007221655337057224590061020154002960080889053322580902100686953300210200953162478210953300006973528002平均值127658222197401292579900712914942002
根据3种算法得到不同转速下的主轴回转精度,如表2所示。以最小二乘迭代算法结果为基准,最小二乘近似算法结果和迭代算法结果基本一致。在有些转速下,平均值算法略优于近似算法。在实际应用中可综合最小二乘近似算法和平均值算法,根据表1中的总距离指标,选用相应的算法对电主轴的回转精度进行评价。
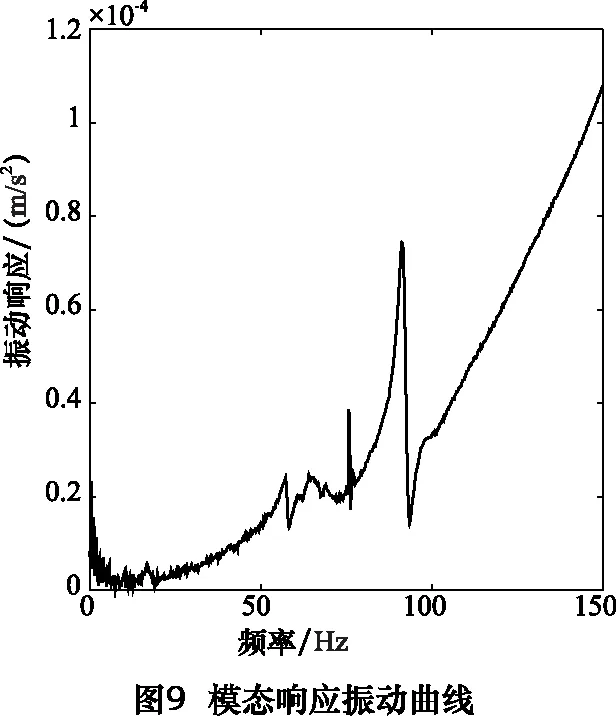
由表2可得在5 400 r/min转速,其精度发生突变。通过对电主轴进行模态试验,可得到图8、9所示模态试验响应图。由图可得,当频率处于92 Hz时,相位180°反向,且振动响应出现尖锋,即92 Hz为电主轴一阶固有频率,换算成电主轴转速即为5 520 r/min。可证明本实验数据处理算法的准确性,并可采用本检测方法来检测机构的低阶固有频率。

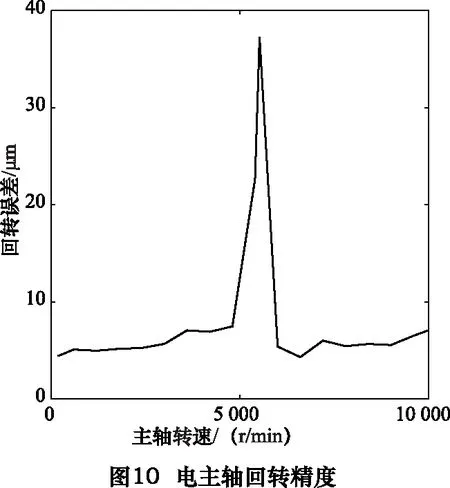
最后采集5 520 r/min转速下的误差信号,并综合最小二乘近似算法和平均值算法分析,得到最终的电主轴回转误差曲线,如图10所示。
4 结论
通过本文分析,在不考虑时间成本的情况下,可直接采用最小二乘牛顿迭代算法计算主轴回转精度,其计算精度高,但计算时间长。
在需要考虑时间成本的情况下,可选用下面两种计算方法:
(1)直接采用最小二乘近似算法评估主轴回转精度。该方法计算时间短,精度较高。
(2)采用最小二乘近似算法和平均值算法分别评估主轴回转精度,若结果一致,则选用任意一种评价结果。反之,则比较两种算法的最小二乘圆精度,选用更高精度最小二乘圆下的计算结果。该方法计算精度较上一种更高,计算时间略长。其相对于迭代算法,计算精度相差不大,但计算时间远小于迭代算法,是一种兼顾计算精度和效率的快速评价算法。
表2 三种算法回转精度对比
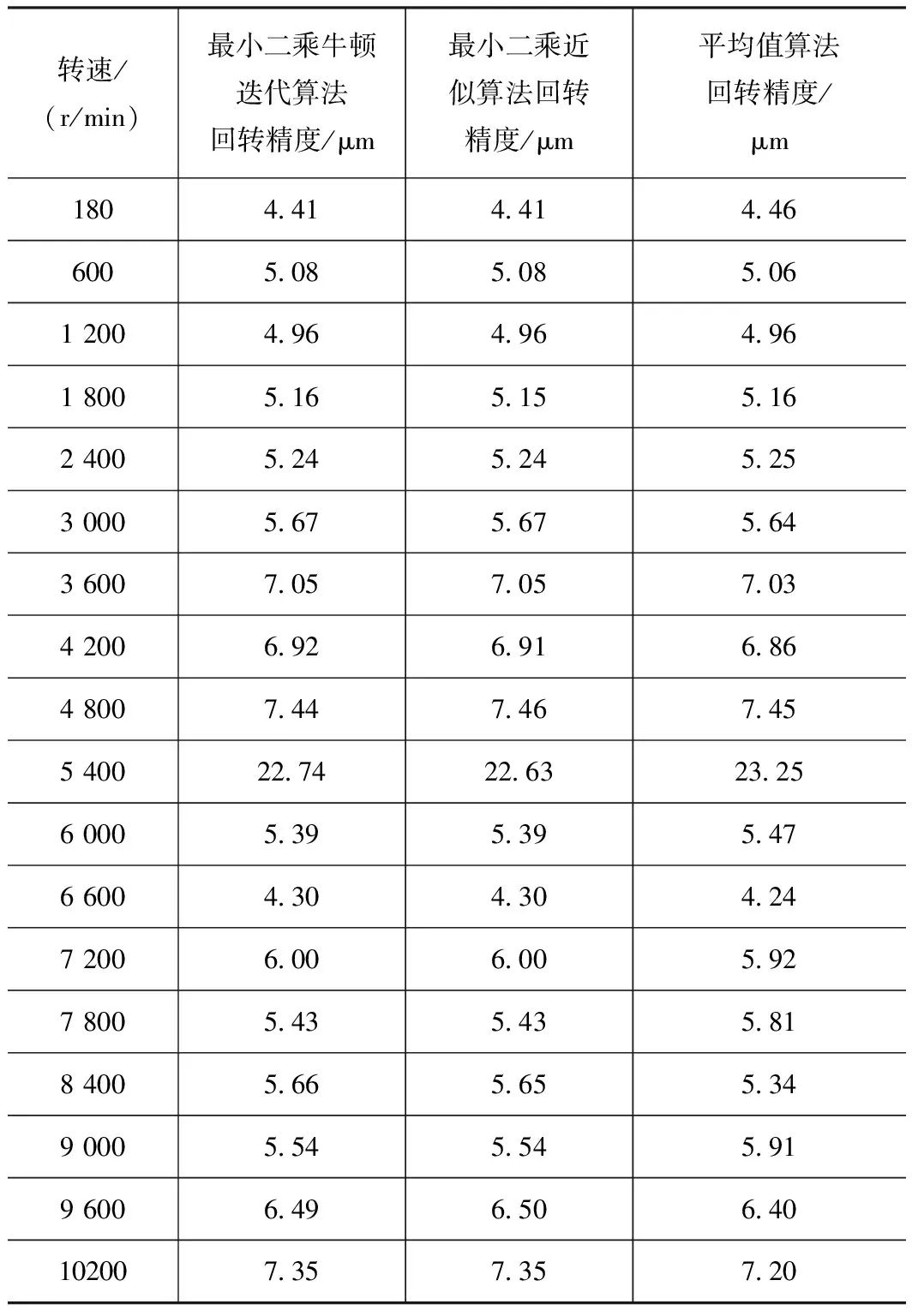
转速/(r/min)最小二乘牛顿迭代算法回转精度/μm最小二乘近似算法回转精度/μm平均值算法回转精度/μm18044144144660050850850612004964964961800516515516240052452452530005675675643600705705703420069269168648007447467455400227422632325600053953954766004304304247200600600592780054354358184005665655349000554554591960064965064010200735735720
[1]王立平. 数控机床先进技术浅谈[J]. 航空制造技术, 2010(10): 49-52.
[2]赵钦志, 王立平, 王军见. 数控机床可靠性试验和评估技术分析与研究[J]. 制造技术与机床, 2017(11): 17-21.
[3] 张根保, 王立平. 国产数控机床可靠性技术综述[J]. 航空制造技术, 2013(5): 26-31.
[4] 张彬彬, 王立平, 吴军. 3自由度并联机构的动力学各向同性评价方法[J]. 清华大学学报:自然科学版, 2017, 57(8): 803-809.
[5]GB/T 17421.7—2016,全国金属切削机床标准化技术委员会.机床检验通则 第7部分:回转轴线的几何精度[S]. 北京:中国标准出版社, 2016.
[6]Test code for machine tools -- Part 7: Geometric accuracy of axes of rotation: ISO 230-7:2006 [S/OL].https://www.iso.org/standard/56624.html,2015-05-15.
