基于三值光计算机的细胞自动机计算系统

李 梅

(西安工业大学 计算机科学与工程学院，陕西 西安 710021)

0 引 言

三值光计算机[1-3]，经过几次大的理论突破，现已发展成为能够并行处理百位量级三值逻辑运算的实验系统[4-8]。文中在此实验系统上实现大规模二维三值细胞自动机的演化计算，把细胞自动机的天然并行性和三值光计算机的数据位巨并行性结合起来，极大地简化了运算过程的时间复杂性；同时，发挥三值光计算机的运算器可重构性[9]，极大地扩充了细胞自动机演化规律的灵活性和多样性，为细胞自动机的应用创造了更好的条件。

1 三值光计算机的相关特点

三值光计算机是一种光电混合并行数字计算机，通过控制液晶改变光的偏振性完成运算，一次运算可以处理整屏数据，因此三值光计算机拥有巨大的数据位数。同时，依据降值设计理论和方法[9]设计的三值光学逻辑处理器可以规范地为各种二元三值逻辑运算构建专门的运算器单元，具有逻辑运算器的重构性。

2 细胞自动机

细胞自动机是一种具有时间、空间和状态离散性的动力学系统[10-11]，可表示为CA=(Ld,S,N,f)。其中，L为细胞空间，d为细胞空间维数；S为细胞的有限状态集；N表示邻域细胞的组合，可以采用(S1,S2,…,S|N|)表示，|N|是此组合邻域细胞的个数；f表示将(S1,S2,…,S|N|)映射到S的一个状态转换函数。

目前实现细胞自动机有两种方法，用VLSI实现[12]和软件模拟[13]。用VLSI实现，虽然运算速度快、结构简单，但细胞单元之间的局部状态转换规则一旦确定就很难改变。用软件模拟需要逐个计算每个细胞的演化函数，属于串行过程，当规模巨大时效率急剧降低。

3 三值光计算机上实现细胞自动机

3.1 三值逻辑运算

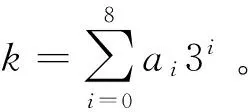
表1 二元三值逻辑函数真值表

有了上面的运算编号，就可以给三值光计算机完成的特殊运算Θ给予定义：

定义1：设A，B是大小为m×n的矩阵，其中矩阵元素ai,j,bi,j∈{0,1,2}，i∈{0,1,…,m-1},j∈{0,1,…,n-1}。运算Ψ1,Ψ2,…,Ψm×n∈M，AΘB是矩阵对应元素做三值逻辑运算，并且矩阵每位的运算方式都可不同，如下所示：

三值光计算机可以在一个时钟周期内完成两个大规模矩阵的AΘB运算。

3.2 实现三值逻辑运算的器件

基于降值设计理论(decreased-radix design principle，DRDP)设计实现的三值逻辑光学处理器是三值光计算机的核心器件，能够完成任意二元三值逻辑运算。

3.2.1 理论的主要内容

降值设计规律可以表述为：在选择用来表示N值信息的N个物理状态中，如果包含一个特殊的物理状态—D状态，则迭合n×n×(n-1)个运算基元中不超过n×(n-1)个运算基元就可以构造出任一个N值逻辑运算器(共有n(n×n)个)。

从降值设计规律中抽取出降值设计理论，该理论的核心内容为：“D”是一个特殊物理状态，它与任何其他状态A相遇后结果仍是状态A；如果用来表示信息的物理状态中包含一个状态“D”，则n(n×n)个n值逻辑运算器中的任一个都可以按照规范的降值构造步骤，组合n×n×(n-1)个运算基元中的几个而成。

3.2.2 通用降值设计规范

(1)写出待设计的逻辑运算器的真值表；

(2)确定元素d的值，通常就是逻辑运算真值表的C列中出现次数最多的那个逻辑值，并确定集合W与集合F的元素为一一对应关系(其中d与D对应)；

(3)写出与真值表对应的物理状态迁移表；

(4)对物理状态迁移表应用分解定理，得到若干个基元表；进而得到对应的运算基元的编号，即标准设计组件的编号；

(5)用迭合器实现各运算基元的迭合操作，实现逻辑运算器。

3.2.3 运算器件构造

图1是实现的三值逻辑运算的一种基元的光学硬件结构。其中，a和b为光输入端，c为光输出端；h1和h2为水平偏振片，它能吸收垂直线偏振光V透过水平线偏振光H；v1为垂直偏振片，它能吸收水平线偏振光H透过垂直线偏振光V；矩形框Lc为光控液晶单元，虚线是它的光控端，当其光控端有光时，Lc能控制穿过它的光束的偏振方向旋转90度，而当其光控端无光时，穿过它的光束的偏振方向保持不变。

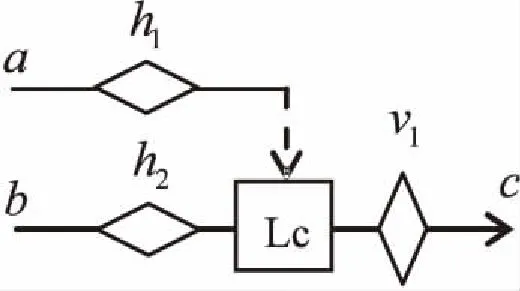
图1 某处理基元的光学硬件结构

此光路的工作原理为：h2、v1和Lc构成了一路光阀，当a是无光态(W)或垂直线偏振光(V)时，由于水平偏振片h1的作用，Lc的光控端无光，于是光阀关闭，此时无论b是什么状态，输出端c均为无光态(W)；当a是水平线偏振光(H)时，水平线偏振光能透过h1到达Lc的光控端，即光阀打开，此时，如果b是水平线偏振光(H)，则它透过h2，再经Lc的旋光后成为了垂直线偏振光(V)，之后透过v1后到达输出端c，即c为垂直线偏振光(V)，而当b是无光态(W)或垂直线偏振光(V)时，由于水平偏振片h2的作用，输出端c均为无光态(W)。其他的光学运算基元均可以用类似的硬件结构实现。

总结运算器的18种运算基元的光路结构，它们具有相似的结构—两个偏振片加一个液晶像素。其差别在于偏振片的偏振方向和液晶的静态旋光性。基于处理基元光路结构的运算器结构如图2所示。根据液晶阵列左右所贴偏振片的偏振方向的不同，划分为四个相等的区域：即V-V区、V-H区、H-H区和H-V区。

图2 运算器结构

3.3 二维三值细胞自动机的数学建模

运算器是三值逻辑光学处理器的关键部件，它由众多光学运算基元构成，这些基元共有18(3×3×(3-1))种。下面以18种光学运算基元中的某一种为例，说明其硬件结构。

在三值光计算机平台上实现的细胞自动机是二维三值细胞自动机，其参数d=2，S={0,1,2}。根据三值光计算机计算平台的特点，需要重新定义N和f的表示方法。

首先确定N，如图3所示，把被关注的细胞标为0，然后从0号细胞开始顺时针旋转，从而可以对细胞自动机的任意一个细胞的邻域细胞进行编号。例如向量N(0，3，7)表示图3中间的细胞周围与其有关系的细胞有三个，分别是自己、右邻域细胞、左邻域细胞。

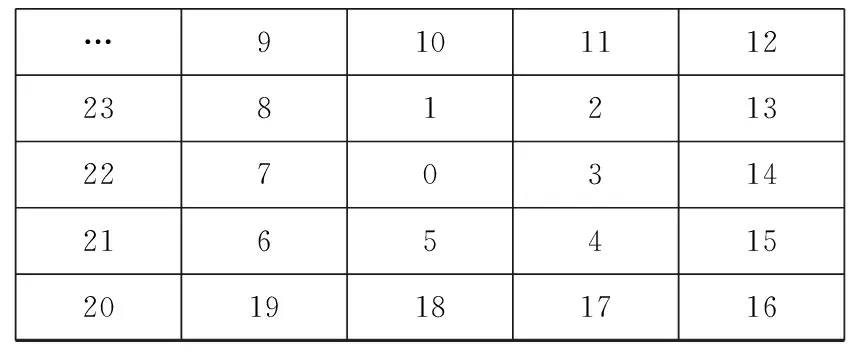
…91011122381213227031421654152019181716

图3 邻域细胞的编号规则

至此，(N：F)就可以唯一地表示一种细胞自动机变换规则。例如(N：F)=((0，3，7)：(243，19062))，表示细胞自动机的一个细胞的状态转换函数为：此细胞与右邻域细胞做243号运算，结果再与左邻域细胞做19062号运算。需要强调的是，构建的细胞自动机的每个细胞的邻域细胞组合N必须相同，F可以不同，通过F的不同可以体现细胞自动机的高可控性。

图4是一个改进后的细胞自动机的例子，每个细胞的转化规则都不同。图中就是一个由16个细胞组成的二维三值细胞阵列，每个细胞的状态转化函数由填写在细胞处的两个向量表示。如第一行第一列的细胞((0,1,3):(15471,17421))表示此细胞下一时刻状态由此细胞分别和上、右邻域细胞做15471号、17421号逻辑运算所得的结果决定。此细胞的右邻域细胞是第一行第二列，上邻域细胞有两种选择，零边界时直接是0，循环边界是第四行第一列。

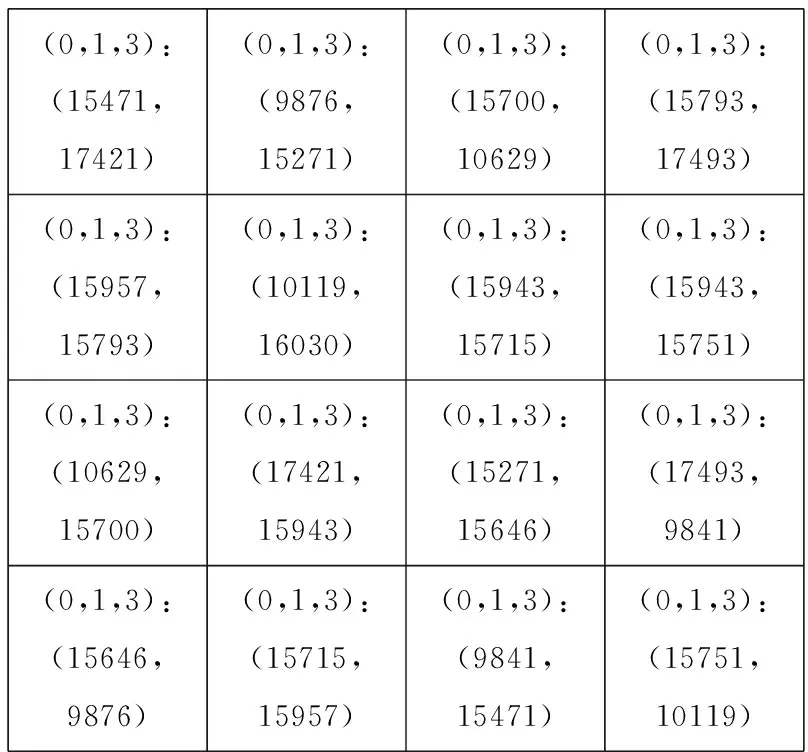
(0,1,3):(15471,17421)(0,1,3):(9876,15271)(0,1,3):(15700,10629)(0,1,3):(15793,17493)(0,1,3):(15957,15793)(0,1,3):(10119,16030)(0,1,3):(15943,15715)(0,1,3):(15943,15751)(0,1,3):(10629,15700)(0,1,3):(17421,15943)(0,1,3):(15271,15646)(0,1,3):(17493,9841)(0,1,3):(15646,9876)(0,1,3):(15715,15957)(0,1,3):(9841,15471)(0,1,3):(15751,10119)

图4 改进后的三值二维细胞自动机

3.4 错位叠加运算

三值逻辑光学处理器的解码器能够读出每一条信号光线携带的信息，根据在V-V区、V-H区、H-H区和H-V区(如图2所示)的相应位置通过判断有无光而非光强大小，即可精确解码，将光信号数据转换成电子信号数据输出显示。

例如，要计算一个大小为m×n的细胞自动机CA=(L2,{0,1,2},N,f)，每个细胞的变化规则是(N:Fi)，0

下面是错位叠加计算的具体方法。用矩阵A表示二维三值细胞阵列，每一个细胞的状态由ai,j表示。如图5所示，把矩阵A的所有数据循环左移一个单位构成矩阵B。AΘB的运算结果矩阵C就是细胞阵列A的所有细胞与其右邻域细胞做逻辑运算的结果；再把矩阵A的所有数据循环下移一个单位构成矩阵D，DΘC的运算结果形成矩阵E，也就是细胞阵列A的所有细胞与其上邻域细胞做逻辑运算的结果。这样细胞阵列A与右邻域细胞以及上邻域细胞所做的逻辑运算的结果分别获取成功。

图5 用三值光计算机完成细胞自动机的状态转移

由于建立的细胞自动机计算模型的N相同，也就是每个细胞的状态转化规则的邻域细胞组合相同，而运算规则不同。利用三值光计算机做AΘB运算，每位运算规则都有不同的特点，可以并行完成所有细胞与周围细胞做逻辑运算(N:Fi)，至此一次细胞自动机的迭代计算完成，实现了二维三值细胞自动机的并行演化计算。

4 实验验证

在三值光计算机平台上实现细胞自动机计算系统，完成细胞自动机的演化计算的时间复杂度与细胞自动机的细胞数目无关，只与细胞自动机所选状态转换函数的|N|有关，而且每个细胞的运算规则都是可控的。

目前，已经实现的百位量级三值逻辑运算的实验系统可以完成由42个细胞组成的细胞自动机的演化计算。以图4中规定的转化规则对4×4的二维细胞自动机进行零边界演化计算，结果如图6所示。

该实验系统采用的是市面上常见的串行控制显示器液晶屏，虽然目前还无法充分体现系统的并行优势，但是目前全像素并行控制的液晶模块已经设计定做完成，而且增加数据宽度在理论上已经趋于完善，可实用的三值光计算机指日可待。

图6 实现细胞自动机一次演化计算

5 结束语

实现的高速大规模可控细胞自动机计算系统提高了细胞自动机的演化计算速度和复杂度，为细胞自动机在密码学[14-17]、伪随机序列生成[18-19]、复杂系统模拟[20-21]等领域的应用开辟了一条新的途径。

[1] 金 翊，何华灿，吕养天.Ternary optical computer principle[J].Science In China:Information Sciences,2003,46(2):145-150.

[2] JIN Yi,HE Huacan,LÜ Yangtian.Ternary optical computer architecture[J].Physic Scripta,2005,118:98-101.

[3] JIN Yi,HE Huacan,AI Lirong.Lane of parallel through carry in ternary optical adder[J].Science in China:Series F,2005,48(1):107-116.

[4] 包九龙,金 翊,蔡 超.三值光计算机百位量级编码器的实现[J].计算机技术与发展,2007,17(2):19-22.

[5] 黄伟刚,金 翊,艾丽蓉,等.三值光计算机百位编码器的设计与构造[J].计算机工程与科学,2006,28(4):139-142.

[6] 金 翊.三值光计算机高数据宽度的管理策略[J].上海大学学报:自然科学版,2007,13(5):519-523.

[7] 詹小奇，彭俊杰，金 翊，等.三值光计算机数据位资源的静态分配策略[J].上海大学学报:自然科学版,2009,15(5):528-533.

[8] 张赵云,金 翊,严军勇,等.三值光计算机远程交互系统

设计与实现[J].计算机工程与设计,2009,30(10):2411-2413.

[9] YAN Junyong,JIN Yi,ZUO Kaizhong.Decrease-radix design priciple for carrying/borrowing free multi-valued and application in ternary optical computer[J].Science in China:Series F,2008,51(10):1415-1426.

[10] WOLFRAM S. Statistical mechanics of cellular automata[J].Reviews of Modern Physics,1983,55(3):601-644.

[11] WOLFRAM S.Theory and applications of cellular automata[J].World Scientific,1986,43(12):1346-1357.

[12] 王 颖,陈 禾.细胞自动机在VLSI测试中的应用[J].北京理工大学学报,2007,27(5):432-435.

[13] 吕晓阳,孔令江,刘慕仁.细胞自动机的演化与计算理论[J].华南师范大学学报:自然科学版,1996(2):43-49.

[14] 韩建飞.基于细胞自动机的流密码的设计与应用研究[D].西安:西安电子科技大学,2014.

[15] 张文涛,卿斯汉,吴文玲.对一个基于细胞自动机的分组密码变形的分析[J].软件学报,2004,15(5):767-771.

[16] 王晓东,王丽丹,段书凯.基于忆阻细胞自动机的图像像素值置换加密技术[J].计算机科学,2013,40(9):133-135.

[17] 夏学文,李元香,曾 辉.基于耦合触发细胞自动机的图像加密算法[J].计算机科学,2009,36(2):214-219.

[18] 张传武.细胞自动机组合伪随机序列发生器[J].电子科技大学学报,2008,37(5):716-719.

[19] 赵建林,方 勇,杨 玲,等.基于2-by-n细胞自动机的伪随机序列发生方法研究[J].成都信息工程学院学报,2008,23(1):73-77.

[20] 时宁国,解亚萍.基于细胞自动机的城市用地仿真研究[J].系统仿真技术,2010,6(3):192-196.

[21] 于乃功,阮晓钢.细胞自动机及其在复杂系统研究中的应用[J].计算机工程与应用,2004,40(12):25-28.