基于片段的企业信任网络演化图聚类算法
2018-03-20卢志刚解婉婷
卢志刚,解婉婷
(上海海事大学 经济管理学院,上海 201306)(*通信作者电子邮箱575246242@qq.com)
0 引言
在大规模、开放的网络环境中,企业由于业务行为而产生信任关系,企业间的信任关系可构成一个信任网络。由于企业信任关系是高度动态的,因此信任网络也随时间而演变。研究企业信任网络结构随时间的演变、发现网络中的隐式社区[1]、找到内部信任关系稳固的信任联盟、检测联盟解散或合并的时间节点,可帮助企业直观、准确了解自身所处的动态联盟,通过协同合作取得规模效益,保持竞争活力。
早期关于信任网络的研究主要集中在静态网络的联盟发现,也涌现出大量方法(基于模块度优化方法[2-3]、基于谱分析方法[4]、基于信息论的模拟退火算法[5]等)。
近些年,关于信任网络的研究集中于动态网络的社区演化,主要分为以下两类。第一类是基于时空独立评价的方法[6-7],这种方法将网络结构划分和演化评价区分开,用静态网络发现算法识别单时间快照上的网络结构,再对相邻时间的网络结构变化进行对比分析,得到网络演变信息。另一类是基于时空集成评价的方法,利用短时平滑性假设,以相邻时间的网络结构差异度最小为优化目标,设计动态网络划分算法,包括扩展静态社区评价体系的方法[8-9]、基于进化聚类的方法[10]、基于隐空间的动态网络划分方法[11]等。
以往对动态信任网络的研究基于短时平滑性假设,优化目标通常是发现核心联盟,无法及时发现由外部环境或是网络内部引发的联盟突变等。本文统筹考虑网络演化的短时平滑性和结构突变的可能,提出基于片段的企业信任网络图聚类(Graph Clustering, GC)算法,以期发现一段时间内网络演化的稳定结构和结构突变的时间异常点,从而高效发现联盟和跟踪网络。
1 企业信任网络演化
在开放环境中,处于远离平衡态的企业信任网络在随机因素扰动(即系统的涨落)的诱发下,自发从不稳定态跃迁至一个新的稳定态[12]。涨落是企业信任网络达到有序状态的根本原因,导致信任网络演化重大涨落的因素称为关键事件。研究企业信任网络演化,就是识别企业交互过程中关键事件发生的时间点,发现不同时间段下信任网络的稳态结构。现采用图的形式来描述企业信任网络演化,具体如下。
在企业实体交互过程中,通常一方为求信方,一方为获信方,它们之间的信任关系可形成一个信任网络图。企业实体为网络中的顶点,其集合记为V;企业间信任关系为网络中的边,其集合记为E。设企业信任网络顶点集V可分割为两个子集{I,J|I∩J=∅,I∪J=V},子集I为求信企业集合,子集J为获信企业集合,则企业信任网络可表示为图G=(I,J,E)。记企业实体ai与bj间的信任关系为eij,∀eij∈E,有ai∈I,bj∈J,故G满足二分图结构。
将信任网络G转化为二分图表示,并考虑网络演化的时间信息。设T={1,2,…,t,…}为时间戳集合,t是企业信任网络在时间轴上的唯一标识,则信任网络的演化可表示为如图1所示。时间戳集合为T={t,t+1,t+2,t+3,t+4},求信企业集合为I={a1,a2,a3,a4},获信企业集合为J={b1,b2,b3},企业节点集合I和J不随时间变化,信任关系集合E动态变化,则信任网络G随时间演化。为反映信任网络随时间的演化过程,给出如下定义。
定义1 信任网络流。设时间戳t下的信任网络为Gt,则不同时间戳下企业信任网络的集合称为信任网络流,记为F={G1,G2,…,Gt,…}。
如图1所示,信任网络流为F={Gt,Gt+1,Gt+2,Gt+3,Gt+4}。
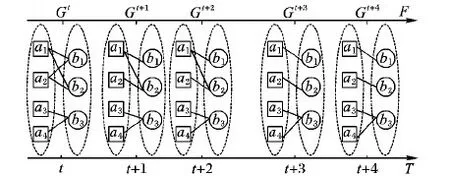
图1 信任网络的二分图描述
为进一步描述信任网络结构随时间的演变,用编码图代替二分图描述信任网络,黑色方块代表企业间具有信任关系,白色方块代表企业间不具有信任关系,如图2所示。对信任网络流进行结构划分,将类型相同的企业节点划分到一个分组里,结构相同的信任网络划分到一个片段里,现给出如下定义。
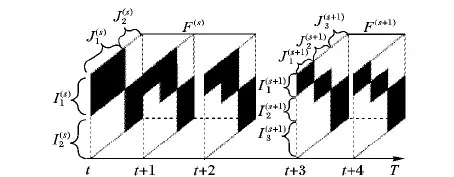
图2 信任网络编码示意图

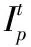
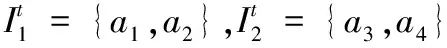
定义5 信任网络片段。设T(s)={ts,ts+1,…,ts+1-1}为第s个时间片段,T(s)所对应的信任网络集合为F(s)={Gts,Gts+1,…,Gts+1-1},若∀t≠t′∈T(s),在Gt和Gt′中,有It=It′,Jt=Jt′,即F(s)中每个信任网络的求信企业分组集合和获信企业分组集合相同,则称F(s)为第s个信任网络片段,ts为关键事件点。记F(s)中求信企业分组集合为I(s),获信企业分组集合为J(s),信任联盟集合为TR(s)。
如图2所示,信任网络流F中有2个信任网络片段,分别是:F(s)={Gt,Gt+1,Gt+2},F(s+1)={Gt+3,Gt+4},t+3为关键事件点。
为了考察企业信任联盟演变机制,研究企业信任网络演化。通过研究信任网络流F的演化结构,识别关键事件点ts和不同时间片段下的企业信任联盟的TR(s),发现企业信任联盟的稳定结构及其变化情况,帮助企业及时调整合作战略,达到联盟企业信息共享、资源互补,实现规模经济,最终取得市场、增强竞争优势。
企业信任网络演化问题的研究思路如图3所示。问题的求解类似于NP-hard问题的求解过程,对诸多可能解所构成的网络演化模型进行编码,通过图聚类算法搜索最优解,以达到发现企业信任联盟演变机制的目的。
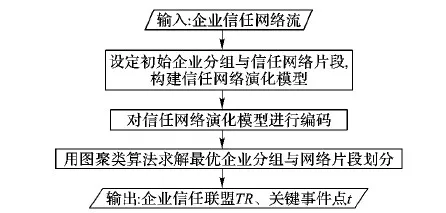
图3 企业信任网络演化问题研究思路
2 企业信任网络编码
将企业信任网络流转化为二进制串对其编码,构建编码成本函数以体现网络结构的复杂程度。通过对企业进行分组来划分信任网络,将结构相同的信任网络组成片段,从而压缩编码,使编码成本达到最小,发现不同时间段下信任联盟的稳定结构。
2.1 信任网络编码与编码成本
2.1.1 信任网络编码
编码信任网络,即将一个含有m个求信企业和n个获信企业信任网络转化为二进制串来描述。如图1中,信任网络Gt含4个求信企业与3个获信企业,其信任关系描述为:
其中:“1”表示求信企业与获信企业之间存在信任关系,“0”表示不具有信任关系,则该信任网络可编码为110 110 001 001(以行排列)。
由于实际中,m与n数值可能较大,直接编码会占用大量存储空间,可采用哈夫曼编码等标准化无损压缩方案来编码,以节约存储空间。由此,信任网络的编码长度可用变为mnH(G),其中H(G)是编码熵,是对矩阵中每个元素最小编码长度的估计:
H(G)=-∑p(x) lbp(x);x∈{0,1}
其中:p(1)=|R|/(mn),表示信任关系的密度,|R|为信任关系总数(矩阵中1的个数)。p(0)=1-p(1)。当矩阵中元素全为1或全为0时,信任网络结构统一,编码熵为0。
2.1.2 编码成本
为了体现信任网络结构的耗散程度,可构建编码成本函数Cg:
Cg=log*|R|+log*m+log*n+mnH(G)
其中,log*表示将整数转化成二进制的通用编码长度。有log*x≈lbx+lb lbx+…,每一项分式只保留正整数位。
编码成本越大,说明信任网络结构越发散;反之,信任网络越统一。
2.2 信任网络企业分组
对信任网络G,可通过对其m个求信企业和n个获信企业进行排列组合,将同类型的求信(获信)企业组织到同一个求信(获信)分组中,把信任网络转化成低熵、均匀的网络结构,以降低编码成本。
为此,引入交叉熵的概念来计算企业节点分配到分组的成本[13]。通过比对不同分配成本来确定企业的分组归属。
以划分求信企业为例,假定某一求信企业ai与l个获信分组中的企业可能有信任关系。ai与获信企业分组的信任关系服从二项分布P。P为真实分布,Pq(1)(1≤q≤l)表示ai与第q个获信企业分组的信任关系密度,则Pq(0)=1-Pq(1)为不信任的关系密度。
将ai所在的求信企业分组与获信企业分组的信任关系定义为非真实分布Q,Q为二项分布,Qq(1)表示该求信企业分组与第q个获信企业分组之间信任关系的密度。
则交叉熵反映了该求信企业与其所在分组内其他求信企业信任关系分布的相似程度,有:
H(Pq,Qq)=∑Pq(x) lbQq(x);x∈{0,1}
H(Pq,Qq)越小,说明信任关系分布越相似,表明它们信任同类型的获信企业,可分配到同一个求信分组。
则ai分配到求信分组的编码成本为:
(1)
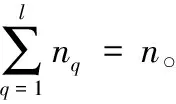
同理,对获信企业执行类似操作,可得获信企业分组。由此,信任网络可以根据求信和获信企业的分组情况重新排列,形成新的网络结构。如图2所示,不同时间戳下的网络根据分组情况划分出各自的网络结构分区。
2.3 信任网络片段编码
对信任网络流F,可以考察其中不同时间戳下的信任网络结构来发现信任联盟关系的演变。将时间相邻且结构相似的信任网络分配到同一个信任网络片段中,则认为联盟结构较为恒定。由此,通过将信任网络划分到不同信任网络片段,可以了解信任网络结构随时间的变化。
对网络片段F(s)={Gt,Gt+1,…,Gtt+1-1}进行编码,成本函数由式(2)给出:
C(s)=Be+Bp+Bl+mH(M)+nH(N)+∑Cg
(2)
式(2)相关函数项的考虑如下。
1)Be考虑求信企业和获信企业的个数m和n。
Be=log*m+log*n
2)Bp考虑求信企业分组个数和获信企业分组个数k和l。
Bp=log*k+log*l
3)Bl考虑信任网络片段中的网络个数ts+1-ts。
Bl=log*(ts+1-ts)
4)H(M)和H(N)考虑求信企业分组分配和获信企业分组分配编码熵。
H(M)是求信企业分组的编码熵,M是概率为mp/m的多元随机变量,mp表示信任网络片段下第p个求信企业分组的大小,1≤p≤k。同样,H(N)是获信企业分组的编码熵,N为概率为nq/n的多元随机变量,nq为第q个获信企业分组的大小,1≤q≤l。
5)∑Cg考虑信任网络片段中不同时间戳下的信任网络编码总成本。
其中:|Rp,q|表示Fp,q中信任关系的总数,|Fp,q|=mpnq(ts+1-ts),是信任分区片段的大小。H(Fp,q)是Fp,q中信任关系的编码熵,定义如下:
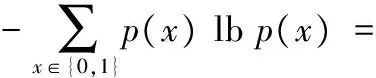
-[γp,qlbγp,q+(1-γp,q) lb (1-γp,q)]
(3)
其中:γp,q=|Rp,q|/|Fp,q|是Fp,q中信任关系的密度,H(Fp,q)量化了Fp,q结构的耗散程度。编码熵越小,说明分区内信任关系越统一;反之,则说明分区内信息关系越混乱。
2.4 信任网络流编码成本
连续的信任网络片段组成了信任网络流,将不同时间段下的信任网络片段编码成本进行累加,得到信任网络流的编码成本C为:
(4)
其中:C(s)是第s个信任网络片段的编码成本,W为网络片段的总数。
编码信任网络流,通过最小化编码成本,试图将信任网络分解成同质的分区,即要么接近完全连接(完全信任),要么完全断开连接(不存在信任关系),从而发现信任网络中关系稳固的信任联盟。将信任联盟稳固的网络置于同一片段中,如果联盟结构突变,则开始新的片段。对网络流编码的目标是在支持足够简单分解的前提下,充分捕捉信任网络结构随时间的变化。
3 图聚类算法
已知信任网络流F,通过企业分组可以重排网络结构,找出信任网络潜在的分区,发现信任关系密集的信任联盟。再将结构相似的网络归入一个片段中,从而识别结构异常的关键事件点。
为发现信任联盟的稳定结构,识别网络演化中的关键事件点并自动划分时间窗口,提出图聚类算法。算法一共有两步:
1)企业分组。给定网络片段F(s),将企业分组至求信企业分组集合I(s)和获信企业分组集合J(s)。
2)网络流分割。分割信任网络流F,识别关键事件点ts。
3.1 初始化
开始一个新的信任网络片段,需要初始化分组数量和分组内的企业分配。针对不同的情况,提出两种初始化方案:
1)全新开始,即处理企业信任网络流中第一个信任网络的初始化。通常做法是将求信企业分组和获信企业分组个数k和l的初始值设为m和n,即一个企业节点构成一个分组集合,第一个信任网络构成初始信任网络片段,再执行算法1进行最优分组搜索。
2)重新开始,即重新开始一个新信任网络片段时的初始化。时间连续的演化网络在结构上具有相似性,在搜索过程中利用这种相似性,即开始一个新片段时,令求信(获信)企业分组数量为上一个片段下的求信(获信)企业分组数量,即k(s+1)=k(s),l(s+1)=l(s)。同样,也依据求信企业分组集合I(s)和获信企业分组集合J(s)对下一个片段的I(s+1)和J(s+1)进行初始化。
3.2 企业分组
已知信任网络片段F(s),对求信企业和获信企业进行分组。核心思想是遍历初始分组分配,在调整分组数量k和l的同时,更新求信企业分组和获信企业分组内。具体来说,交替执行以下两个步骤,直到编码成本达到最小:
1)更新求信企业分组。对于每个求信企业,将其分配给产生最小分组成本的求信企业分组。
2)更新获信企业分组。对于每个获信企业,将其分配给产生最小分组成本的获信企业分组。
算法1 企业分组算法。
Input:信任网络片段F(s),初始企业分组划分集合I(s)、J(s)。
Output:更新后的分组划分集合I(s)、J(s),信任联盟集合TR(s)。
//合并
1)找到求信企业分组(Ip,Ip′),满足Ip,Ip′合并后产生更小的编码成本。
2)根据式(2)计算片段编码成本,如果总编码成本下降,则将Ip,Ip′合并。
3)重复1)~2)步骤,直至结果不再变化。
//分离
4)遍历所有求信企业分组,根据式(3)找到具有最大平均熵的分组。
5)对该分组的每个求信企业执行以下步骤:如果没有该企业,分组的平均熵减少,则将该企业标记为分组转移企业。
//更新
6)对于每个分组转移企业,将其分别归入到k个求信分组里,根据式(1)分别计算分组分配成本,将其分配给产生最小分组分配成本的求信企业分组。
7)重复4)~6)步骤,直至结果不再变化。
8)以同样的方法搜索获信企业分组,直至结果不再变化。
//寻找信任联盟
9)在求得最佳信任分组划分方案后,执行以下步骤:
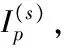
11)对于没有合并的获信企业分组,执行上述步骤。
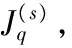
13)对于没有合并的求信企业分组,再执行上述步骤。
14)重复步骤9)~13),直至所有的求信企业分组和获信企业分组都被分配到信任联盟中。
15)输出信任联盟划分集合TR(s)。
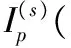
3.3 网络流分割
当新的信任网络到达时间轴,通过构建信任网络片段的增量网络来计算编码成本。如果新的信任网络加入当前网络片段后会产生较大的压缩效益,则算法会将新的信任网络与当前信任网络片段进行压缩编码;否则开始一个新的信任网络片段。具体算法如下。
算法2 网络流分割算法。
Input:信任网络片段F(s)及其编码成本c0,新的信任网络Gt。
Output:更新后的网络片段,新的信任分组分配方案I(s)、J(s)。
1)计算新的信任网络Gt归入片段F(s)后新编码成本cn。
2)将Gt作为一个新的网络片段,计算Gt的编码成本c。
//检查是否有编码益处
3)如果c+c0>cn,则将Gt归于片段F(s)。
4)对于更新后的片段F(s)执行算法1,重新搜索k,l。
5)如果c+c0 6)对于新的片段F(s+1)执行算法1,搜索k,l。 设企业信任网络流包含100个求信企业,100个获信企业,105个时间戳。企业节点个数不随时间改变,企业间信任关系随时间动态变化。为了方便后续实验,对求信企业节点使用1~100进行唯一编号,对每个获信企业使用101~200进行唯一编号。使用R语言ggplot2包中的Tile plot图来展现求信企业和获信企业之间的信任关系,横坐标表示求信企业节点,纵坐标表示获信企业节点,黑色方块表示求信企业与获信企业之间存在信任关系。初始时刻企业间信任关系如图4所示。 图4 企业初始信任网络 在模拟数据集上运行GC算法。表1是GC算法对于企业信任网络流中信任网络片段分割和信任联盟的发现结果。 表1 GC算法运行结果 在表1中,s为对信任网络片段的编号,GC算法将105个信任网络划分到9个网络片段中。ave_trust为每个信任网络片段中平均每个信任网络含有信任关系的数量,num_graph为每个信任网络片段中信任网络的个数,num_TR为每个信任网络片段中信任联盟的个数。 对于每张信任网络,GC算法都能挖掘出网络图的隐藏结构,划分求信企业分组和获信企业分组,找出信任联盟。第一个信任网络片段的信任联盟划分如下: TR1={1,6,11,12,33,40,43,46,47,52,70,72,79,86,101,104,109,110,124,125,142,149,155,156,158,168,169,173,175,176,177,185,196,197,198} TR2={2,20,23,24,30,31,32,35,53,59,67,73,87,90,92,103,108,113,114,132,143,145,147,150,151,152,162,165,167,172,174,178,184,186,191} TR3={3,17,25,26,28,51,55,58,78,80,84,91,93,94,105,123,126,135,141,154,188,193,195} TR4={4,34,38,39,44,54,68,74,75,102,107,171,179,182,200} TR5={5,9,10,19,27,36,37,41,56,61,62,63,64,66,69,88,98,106,130,138,153,161,189,192} TR6={7,18,48,57,60,76,95,96,97,100,111,112,115,116,117,119,122,129,136,137,144,146,160,164,180,181,187,190,199} TR7={8,13,14,42,82,83,131,133,136,140,148,157,159,163,183,194} TR8={15,16,21,22,29,45,49,50,65,71,77,81,85,89,99,118,120,121,127,128,134,139,166,170} 为了能在Tile plot图上清晰展示信任联盟的结构,对企业节点重新标号,具体算法如下:在区分求信企业和获信企业的基础上,根据求信企业分组中企业节点的最小标号对信任联盟进行排序,按信任联盟的顺序对求信企业依次重新标号,要求同一个求信企业分组内的企业节点拥有相邻标号。再对获信企业分组中的企业节点用相同方法重新标号。对第一个信任网络片段中的企业节点执行上述操作,重新标号后,联盟划分如下: TR1={1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120} TR2={16,17,18,19,20,21,22,23,24,25,26,27,28,29,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168} TR3={30,31,32,33,34,35,36,37,38,39,40,41,42,43,121,122,123,124,125,126,127,128,129} TR4={44,45,46,47,48,49,50,51,52,53,54,185,186,187,188,189,190} TR5={55,56,57,58,59,60,61,62,63,64,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147} TR6={65,66,67,68,69,70,191,192,193,194,195,196,197,198,199,200} TR7={71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,176,177,178,179,180,181,182,183,184} TR8={86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,167,168,169,170,171,172,173,174,175} 使用企业节点重新标号后的信任网络来绘图,结果如图5所示,企业信任网络结构变得非常清晰。 若采用第一个信任网络片段中的标号方案,绘制第9个信任网络片段中的信任网络,结果如图6(a)所示,发现信任网络的结构已经变得非常混乱,之前信任联盟的边界变得非常模糊。根据第9个信任网络片段中信任联盟划分方案对企业节点进行标号,重新绘制信任网络,如图6(b)所示。对比两个信任网络,可发现企业信任联盟随着时间演变,不断经历着解散、重组与合并。 将GC算法与GN(Girvan-Newman)算法、FN(Fast Newman)算法这两种经典算法进行对比。实验均由Dev-C++实现,硬件环境为Intel Core i5- 3230 CPU 2.60 GHz,操作系统为Windows 10。实验通过在模拟数据集上运行这3种算法,采用6种经典评价指标来衡量聚类结果的优劣这6种指标分别为:纯度(purity)、精准率、召回率、F值、兰德指数(Rand Index, RI)、标准化互信息(Normalized Mutual Information, NMI)。 图5 重编码后的信任网络 图6 信任网络编码前后对比 纯度的计算公式为: purity=cor_num/num 其中:cor_num为正确聚类企业的个数,num为聚类企业总数。 精准率(P)、召回率(R)、F值和兰德指数(Rand Index, RI)均采用排列组合原理去评价聚类结果,计算公式分别式(5)~(8)所示: (5) (6) (7) (8) 其中:TP(True Positive)指被聚在一类的两个企业被正确聚类了,TN(True Negative)指不应该被聚在一类的两个企业被正确分开了,FP(False Positive)指不应该被聚在一类的企业被错误地聚在了一类,FN(False Negative)指不应该分开的企业被错误的分开,β为权重系数,在下面的实验中,β取值为1。 标准化互信息(NMI)是信息论中的一种度量[15],通过熵的形式来衡量聚实验结果和标准结果的重合程度,计算公式如式(9)所示: (9) 其中:C和C′分别表示真实联盟标签和算法聚类结果;H(C)和H(C′)分别表示联盟标签和聚类结果簇大小分布的熵;MI(Mutual Information)为C和C′的交互信息,如式(10)所示: (10) 上述指标从多种角度来衡量实验结果与标准结果之间的差距,取值都在[0,1]区间,取值越大说明聚类效果越好。若实验结果接近标准结果,则指标值接近1;若实验结果与标准结果差之甚远,则指标值接近0。 用以上6种指标综合衡量3种算法对企业信任网络的聚类结果的准确性,指标值对比表2所示。 表2 3种算法准确度对比 通过观察比较,发现GC算法的准确度高于其他算法,说明GC算法的聚类结果更加接近于企业真实信任联盟分布情况。 采用人工数据集进行算法性能对比。每个时间戳的人工网络包含50个企业节点、200条左右的企业信任关系,第一个时间片段包含第一个时间戳的企业信任关系数据,第二个时间片段包含前两个时间戳的企业信任关系数据,以此类推。 用3种算法处理这8个时间片段,分别记录不同算法处理每个时间片段所用的时长,来比较算法在计算效率上的性能优劣。实验结果如图7所示。 图7 3种算法计算时间对比 结果发现,随着信任网络快照的更新,GN算法与FN算法均采用“全新处理”的方式,无法通过相邻网络结构的相似性实现快速处理,因此,在小规模网络中,这两种算法的处理时间与数据量成正比,运算效率均低于GC算法。而GC算法基于信息论计算,时间复杂度减小,从而缩短计算时间。除此之外,GC算法利用相邻网络结构的相似性,实现算法性能上的增益。如图7所示,随着数据量的增多,GC算法的处理时间并没有显著上升。当第6个网络快照到达的时候,GC算法检测出信任网络结构的突变,重新计算企业信任分组,处理时间增多,将第6个时间戳标记为一个关键事件点,与预期相符。 该实验说明在处理随时间动态变化的信任网络流时,GC算法更具有性能上的优势,可以快速识别信任联盟和检测网络结构突变的关键事件点。 发现企业信任联盟的稳定结构及其变化,揭示企业信任联盟演变机制,是企业联盟合作的核心问题。本文对信任网络流进行编码,构建编码成本函数来反映网络流结构复杂度,通过图聚类(GC)算法搜索最优结构划分方案以划分时间片段和信任分区,从而找到不同时间段下的信任联盟。不同于其他算法,GC算法不需要用户定义的任何参数,是完全自动的。而且,该算法适用于动态流式环境,随着不断到达的信任网络快照,GC算法可以高效跟踪动态信任网络,自动识别信任联盟的稳定结构和联盟结构突变的时间戳,发现企业信任联盟的演变过程。最后,通过对电商信任网络模拟数据集进行实验,发现GC算法能自动挖掘出有意义的信任联盟,并识别出网络结构突变的关键事件点。在与经典社区发现算法进行性能对比时,发现GC算法的准确性和运行效率方面均优于经典算法。 References) [1] 王莉,程学旗.在线社会网络的动态社区发现及演化[J].计算机学报,2015,38(2):219-237.(WANG L, CHENG X Q. Dynamic community in online social networks [J]. Chinese Journal of Computers, 2015, 38(2): 219-237.) [2] BLONDEL V D, GUILLAUME J L, LAMBIOTTE R, et al. Fast unfolding of communities in large networks [J]. Journal of Statistical Mechanics Theory & Experiment, 2008(10): 155-168. [3] KARRER B, NEWMAN M E J. Stochastic blockmodels and community structure in networks [J]. Physical Review E: Statistical Nonlinear & Soft Matter Physics, 2010, 83(2): 016107. [4] CAPOCCI A, SERVEDIO V D P, CALDARELLI G, et al. Detecting communities in large networks [J]. Physica A: Statistical Mechanics & Its Applications, 2005, 352(2/3/4): 669-676. [5] LANCICHINETTI A, FORTUNATO S. Community detection algorithms: a comparative analysis [J]. Physical Review E: Statistical Nonlinear & Soft Matter Physics, 2009, 80(5): 056117. [6] CSHEN H, CHENG X, CAI K, et al. Detect overlapping and hierarchical community structure in networks [J]. Physica A: Statistical Mechanics & Its Applications, 2009, 388(8): 1706-1712. [7] 张学武,沈浩东,赵沛然,等.基于事件框架的社区进化预测研究[J].计算机学报,2017,40(3):729-742.(ZHANG X W, SHEN H D, ZHAO P R, et al. Research on community evolution prediction based on event-based frameworks [J]. Chinese Journal of Computers, 2017, 40(3): 729-742.) [8] BASSETT D S, PORTER M A, WYMBS N F, et al. Robust detection of dynamic community structure in networks [J]. Chaos, 2013, 23(1): 013142. [9] MUCHA P J, RICHARDSON T, MACON K, et al. Community structure in time-dependent, multiscale, and multiplex networks [J]. Science, 2010, 328(5980): 876-878. [10] LIN Y, CHI Y, ZHU S, et al. FacetNet: a framework for analyzing communities and their evolutions in dynamic networks [C]// Proceedings of the 17th International Conference on World Wide Web. New York: ACM, 2008: 685-694. [11] SARKAR P, MOORE A W. Dynamic social network analysis using latent space models [J]. ACM SIGKDD Explorations Newsletter, 2005, 7(2): 31-40. [12] 成全,焦玉英,陆泉,等.基于耗散结构理论的Wiki社区交流动力机制研究[J].图书情报工作,2008,52(11):62-65.(CHENG Q, JIAO Y Y, LU Q, et al. Dynamic mechanisms of communication in Wiki community based on the dissipative structure theory [J]. Library and Information Service, 2008, 52(11): 62-65.) [13] 查日军,张德平,聂长海,等.组合测试数据生成的交叉熵与粒子群算法及比较[J].计算机学报,2010,33(10):1896-1908.(ZHA R J, ZHANG D P, NIE C H, et al. Test data generation algorithms of combinatorial testing and comparison based on cross-entropy and particle swarm optimization method [J]. Chinese Journal of Computers, 2010, 33(10): 1896-1908.) [14] 冯健,丁媛媛.基于重叠社区和结构洞度的社会网络结构洞识别算法[J].计算机工程与科学,2016,38(5):898-904.(FENG J, DING Y Y. A structural hole identification algorithm in social networks based on overlapping communities and structural hole degree [J]. Computer Engineering and Science, 2016, 38(5): 898-904.) [15] WU J, XIONG H, CHEN J. Adapting the right measures forK-means clustering [C]// Proceedings of the 2009 ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York: ACM, 2009: 877-886. This work is partially supported by the Basic Research Project of Shanghai (15590501800). LUZhigang, born in 1973, Ph. D., professor. His research interests include business intelligence, supply chain optimization. XIEWanting, born in 1994, M. S. candidate. Her research interests include information management, e-commerce.4 实验仿真
4.1 数据集
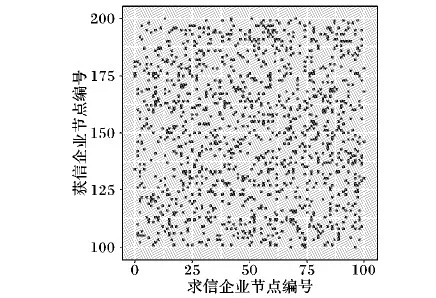
4.2 实验结果
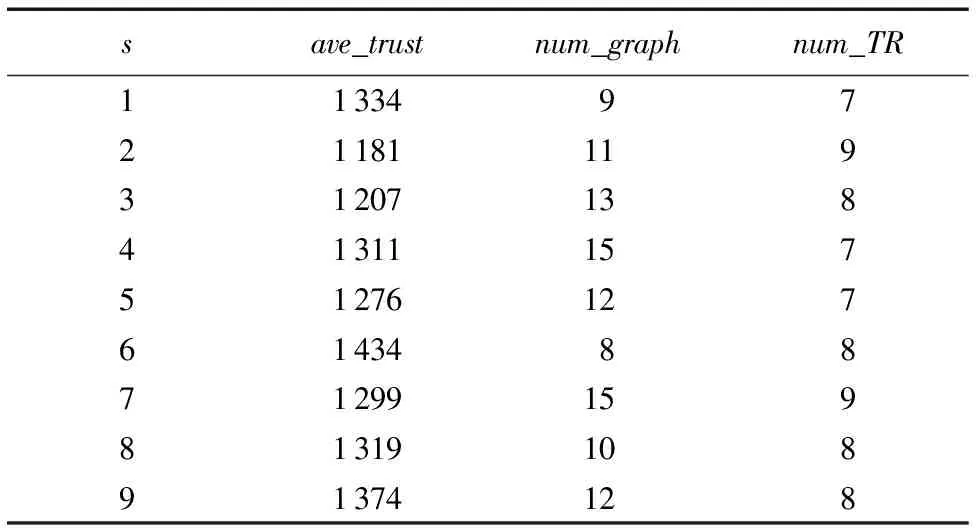
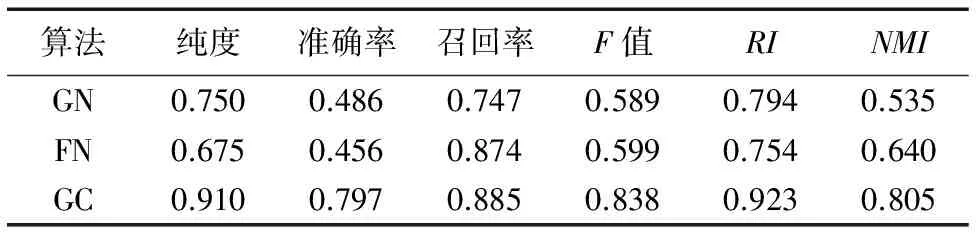
4.3 算法有效性对比

4.4 算法效率分析

5 结语
