具有普适性的改进非负矩阵分解图像特征提取方法
2018-03-20孙福明李豪杰曹玉东
贾 旭,孙福明,李豪杰,曹玉东
(1.辽宁工业大学 电子与信息工程学院,辽宁 锦州 121001; 2.大连理工大学 软件学院,辽宁 大连 116024)(*通信作者电子邮箱gbjdjiaxu@163.com)
0 引言
特征提取是模式识别的关键问题之一,其提取特征的有效性将对识别效果产生重要影响。一般来说,直接对图像进行特征提取后将得到较高维度的特征向量,而通常这些高维特征向量存在较大的冗余,并且很难知道该特征是否有利于识别与分类,从而影响识别的效率与普适性,因此,关于如何获得一种低维有效并具有普适性的图像特征的研究具有重要意义。
目前,特征降维可分为无监督降维方法和有监督降维方法。其中,无监督降维方法包括主成分分析法(Principal Component Analysis, PCA)、局部保持投影法(Locality Preserving Projection, LPP)、稀疏表示法(Sparse Representation, SP)等[1];而有监督降维方法包括离散判别分析(Linear Discriminant Analysis, LDA)、最大边缘准则法(Maximum Margin Criterion, MMC)等[2]。在图像特征提取过程中,基于以上方法可以获得新的特征基与分解系数,而分解系数将作为新的图像特征。从数学的角度来说,新的特征基与分解系数可以是负值,也可以是正值或0,但对于一些特定的应用背景,负值将很难被赋予实际的意义,如图像像素值都是非负的,因此分解得到的基图像中的负值难以被解释和表达。1999年,Lee等[3]提出了一种非负矩阵分解(Nonnegative Matrix Factorization, NMF)的数据降维方法,从而使降维后数据的意义得到了更好的诠释。而后,一些学者将其进行了改进,并应用在了图像识别或分类上,其中包括:从特征的稀疏性考虑,提出了稀疏约束的NMF[4-5];从特征基的相关性考虑,提出了正交约束的NMF[6-7];从不同类别特征的区分性考虑,提出了离散判别约束的NMF[8-9];从特征的非线性特性考虑,提出了流形约束的NMF[10];从特征匹配策略考虑,提出了匹配测量约束的NMF[11-12];从特征向量结构考虑,提出了图正则化约束的NMF[13]等。以上方法分别从不同的角度考虑,采用了不同的约束条件进行非负矩阵分解,从而获得满足各自需求的新的特征基与特征向量。
特征提取与分类器设计是模式识别的两个关键问题,提取出有效的图像特征将会大幅度降低分类器的分类压力。现有的算法虽然可以取得一定的分类效果,但并未针对特征提取方法的普适性进行分析,为此,本文提出了一种具有普适性的基于改进NMF的图像特征提取方法。该方法同时考虑了图像特征的低维性、稀疏性、类间区分性,在原始NMF模型基础上,加入了稀疏正则项与聚类属性正则项,形成了改进的NMF模型,并通过梯度下降法对其进行求解,从而获得新的图像特征。实验表明,在几种常用分类器下,提出的算法获得的图像特征更有利于图像的正确识别或分类。
1 改进NMF模型的建立
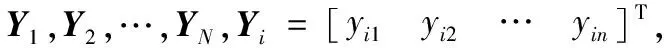
Y≈UV
s.t.uij,vjk≥0
(1)
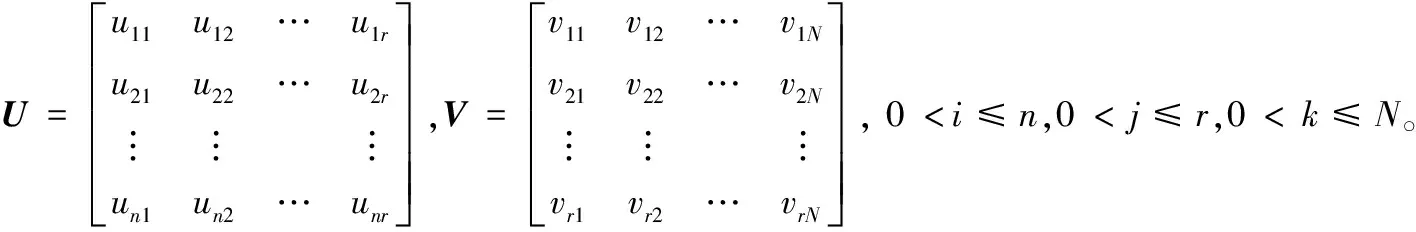
然而,若想获得有效的图像特征,仅仅满足基向量与系数向量非负性是不够的,应对NMF模型增加约束条件,使获得的新的特征向量,即系数向量更有利于图像的分类或识别。以下将从两方面对模型约束条件进行分析:
1)稀疏性。信号稀疏表示的目的就是在超完备字典中用尽可能少的原子来表示信号,获得信号更为简洁的表示方式[14]。而在基于NMF的图像特征提取过程中,则希望在NMF分解得到的基图像中用尽可能少的组合来表示原始图像,从而更容易地获取图像中所蕴含的信息,因此,NMF模型需增加稀疏性约束,如式(2)所示:
(2)
其中α为平衡因子。
根据压缩感知理论,求解V的0范数是一个NP难问题,为求解方便,可以将求解V的0范数转化为求解2范数,如式(3)所示:
(3)
2)聚类属性。对图像进行特征提取时,好的图像特征应满足以下属性,即不同类的图像特征应具有较大的可区分性,这样的特征将更利于正确识别或分类。这里,选用欧氏距离作为特征间相似性的测度函数,那么特征类间区分性可分别用式(4)来表示:
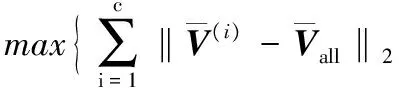
(4)
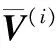
因此,需对NMF模型作进一步的改进,即添加聚类属性约束项,如式(5)所示:

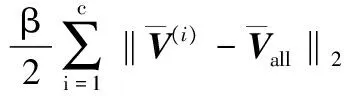
(5)
其中:β为平衡因子。
为方便模型求解,需将式(4)转化为矩阵表达形式。
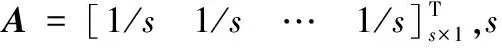
(6)
(7)
这里
再将类间平均特征向量差异转化为矩阵形式。
令
可得式(8):
(8)
(9)
另外,稀疏约束项可由式(10)表示:
‖V‖2=tr(VTV)
(10)
至此,改进的NMF模型可转化为式(11):
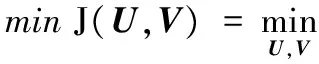
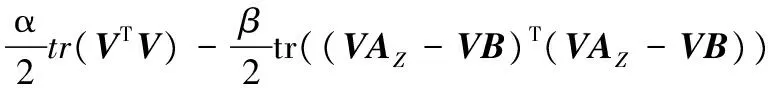
(11)
2 基于梯度下降的模型求解
建立模型后,将采用梯度下降法对该模型进行优化求解,最终求得全局或局部极小值。
经过化简,目标函数式(11)可以转化为式(12):
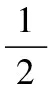
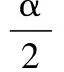
(12)
根据tr(PQ)=tr(QP),式(12)可转化为式(13):
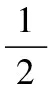
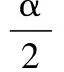
(13)
而后,求解式(13)对U与V的偏导数,如式(14)、式(15):
(14)
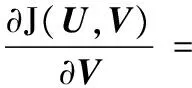
βVAZBT+βVBAZT-βVBBT
(15)
给定U与V的初始值后,将按照以下迭代规则式(16)与式(17)迭代,直至满足停止条件。
(16)
vij,(t+1)←vij,(t)·
(17)
梯度下降具体计算过程如下。
输入量:初始特征矩阵Y,平衡因子α与β。
步骤1 给定初始化矩阵U(0)与V(0),矩阵所有元素均在0与1之间,设置最大迭代次数nmax,迭代误差阈值e,计数器初始化t=0。
步骤2 计数器自增t=t+1。
步骤3 求解式(12)的值J(U(t),V(t))。
如果J(U(t),V(t))
步骤4 对U与V中所有元素按以下规则进行迭代;
vij,(t+1)←vij,(t)·
迭代后进入步骤2。
步骤5 迭代结束,得到最优解U(t)与V(t)。
3 收敛性证明
为证明式(16)与式(17)收敛性,需要引入一个辅助函数。
定义1 如式(18)与式(19)成立,定义G(h,h′)是F(h)辅助函数:
G(h,h′)≥F(h)
(18)
G(h,h)=F(h)
(19)
引理1 如果G是一个辅助函数,则函数F在式(20)迭代更新规则是非增的:
(20)
证明F(ht+1)≤G(ht+1,ht)≤G(ht,ht)=F(ht)。
(21)
因此,通过定义辅助函数,可证明式(16)与式(17)收敛性。
对于目标函数式(11),假设U为独立的变量,可得:
(22)
(23)
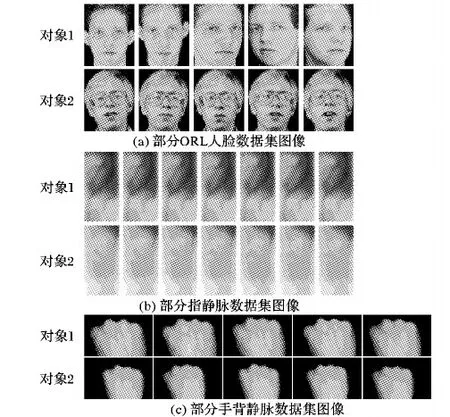
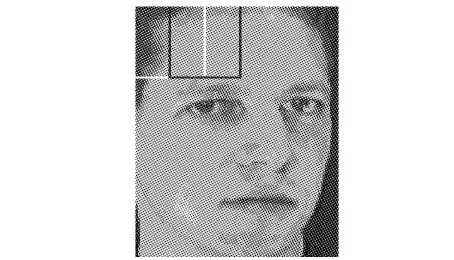
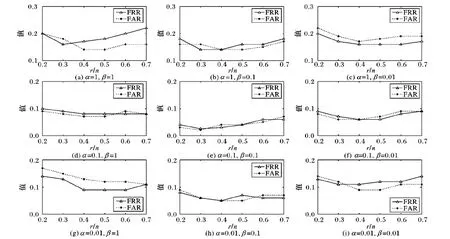
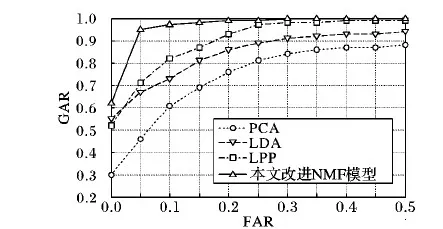
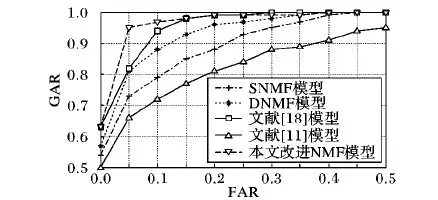
这里,F(u)=J(u),0 引理2 假设U为独立变量,可定义式(24)为辅助函数: (24) 证明 由G(u,u)=F(u),只需证明G(u,uij)≥F(uij)。 将目标函数(11)进行泰勒级数展开,得到式(25): (25) uij(VVT)jj≥uij(VVT)jj (26) 因此,引理2证毕。 对于目标函数式(11),假设V为独立的变量,可得: βVAZBT+βVBAZT-βVBBT)ij (27) (28) 这里,F(u)=J(u),0 引理3 假设V为独立变量时,可定义式(29)为辅助函数: G(v,vij)=F(vij)+F′(vij)(v-vij)+ (29) 证明 由G(v,v)=F(v),只需证明G(v,vij)≥F(vij)。 将目标函数(11)进行泰勒级数展开,得到式(30): (30) (UTU)iivij≥(UTU)iivij (31) (αV)ij=αvij (32) BAZT)jj>vij(AZBT+BAZT-AZAZT-BBT)jj (33) 因此,引理3证毕。 本实验选择3个数据库,即人脸数据集[15]、指静脉数据库[16]、手背静脉数据库[17],其中部分样本图像如图1所示。 图1 部分实验样本示意图 人脸数据库中包含有40个对象,每个对象有10幅图像,共计400幅图像;指静脉数据库包含64个对象,每个对象有10幅图像,共计640幅图像;手背静脉数据库包含38个对象,每个对象包含5至10幅图像不等,共计245幅图像。 此外,实验软件环境为Windows 7操作系统,Matlab 2014b编程工具;硬件为PC,其中,处理器为Intel Core i5- 4460 3.2 GHz,8 GB内存。 改进的NMF模型中共包含3个可调参数,分别为降维后特征维数r、平衡因子α与β。这里,将分别在不同参数组合的条件下进行实验,从而选择最优的模型参数。本实验首先将图像进行分块处理,即每个图像块的大小为32×32像素,而相邻子图像块重叠16像素,并将其作为窗口逐行逐列进行滑动,如图2所示。 图2 样本图像分块示意图 提取每一子图像8个方向的直方图(Histogram of Oriented Gradient, HOG)特征[18],而后逐行逐列融合所有子图像的特征,从而形成图像的初始特征。 当调整模型的参数时,最优的模型参数将可以获得最优的识别结果。这里,令平衡因子α与β分别依次取值1,0.1,0.01;特征维数的取值分别为原特征维数的30%至70%;识别时采用最近邻分类器;样本进行5次交叉检验,使得每一个的图像都有机会成为训练样本和测试样本;并利用错误接受率(False Accept Rate, FAR)与错误拒绝率(False Reject Rate, FRR)作为衡量识别效果的标准。 对于人脸图像数据库,当采用不同模型参数时,实验所得到的FAR值与FRR值分布如图3所示。 图3中的FAR与FRR值是针对不同数据集实验后加权求和得到的,如式(34)与式(35)所示: (34) (35) 由图3可知,对于选择的3种数据集,当平衡因子α=0.1,β=0.1时,FAR值为0.021,FRR值为0.025,进而在该参数下可获得最低的FAR+FRR值,即可获得最优的识别效果,因此,将改进的NMF模型中参数设定为α=0.1,β=0.1。 同样针对应用的3种样本数据库,对图像按4.2节中方法进行初始特征提取,识别时采用最近邻分类器,通过FAR-GAR曲线来对改进的NMF特征降维方法与其他降维方法的性能进行比较,其中GAR(Genuine Accept Rate)为真实接受率。 首先,不考虑降维后图像特征的实际意义,仅仅从数学分析的角度出发,将提出的算法与几类经典的数据降维方法进行比较,即PCA、LDA、LPP降维方法,比较结果如图4所示。 由图4可以看出,当FAR为0.05时,提出的改进NMF模型在识别过程中达到0.96的真实接受率(GAR),高于其他算法GAR值0.21以上;此外,提出的改进NMF模型的FAR-GAR识别性能曲线整体上在其他降维方法的FAR-GAR曲线之上,可说明提出的改进的NMF模型相对于PCA、LDA、LPP可获得更好的识别效果。 然后,考虑降维后图像特征的实际意义,即降维后特征具有非负性特点,将提出的算法与几类常用的NMF降维方法进行比较,这些NMF模型分别从不同的角度出发,对降维后特征分别赋予不同的约束条件,即SNMF(Sparse Nonnegative Matrix Factorization)模型、DNMF(Discriminate Nonnegative Matrix Factorization)模型、匹配测量约束的NMF模型[11]、半监督稀疏约束的NMF模型[18],比较结果如图5所示。 同样,由图5可以看出,当FAR为0.05时,提出的改进NMF模型的GAR值高于其他算法0.14以上;此外,从不同方法的FAR-GAR曲线的位置来看,提出的改进NMF模型的FAR-GAR曲线明显高于SNMF模型、DNMF模型、半监督SNMF模型,略高于匹配测量约束的NMF模型,亦可说明改进的NMF模型在识别效果上的优势。 图3 不同参数下识别效果比较 图4 本文模型与经典降维算法识别性能比较 图5 多种改进NMF算法识别性能比较 本文通过对NMF模型进行分析与改进,提出了一种更具普适性的特征降维与优化方法,其创新点在于考虑新特征稀疏特性的同时,将特征的聚类属性也作为NMF的另一约束项,通过实验验证,提出的算法降维得到的特征更有利于图像的分类或识别。在取得一定效果的同时,仍存在一些问题有待解决,如选择的样本库种类及样本数还需增加,从而进一步提高方法的普适性。 References) [1] SHAN H, ZHANG J, KRUGER U. Learning linear representation of sparse partitioning trees based on unsupervised kernel dimension reduction [J]. IEEE Transaction on Cybernetics, 2016, 46(12): 3427-3438. [2] VLASSIS N, MOTOMURA Y, KROSE B. Supervised dimension reduction of intrinsically low-dimensional data [J]. Neural Computation, 2014, 14(1): 191-215. [3] LEE D D, SEUNG H S. Learning the parts of objects by non-negative matrix factorization [J]. Nature, 1999, 401(6755): 788-791. [4] HAN H, LIU S J, GAN L. Non-negativity and dependence constrained sparse coding for image classification [J]. Journal of Visual Communication and Image Representation, 2015, 26: 247-254. [5] WEN J H, TIAN Z, LIU X Z, et al. Neighborhood preserving orthogonal PNMF feature extraction for hyperspectral image classification [J]. IEEE Journal of Selected Topic in Applied Earth Observations and Remote Sensing, 2013, 6(2): 759-768. [6] POMPILI F, GILLIS N, ABSIL P A, et al. Two algorithms for orthogonal nonnegative matrix factorization with application to clustering [J]. Neurocomputing, 2014, 141(2): 15-25. [7] KOTSIA I, ZAFEIRIOU S, PITAS I. A novel discriminant non-negative matrix factorization algorithm with applications to facial image characterization problems [J]. IEEE Transactions on Information Forensics and Security, 2007, 2(3): 588-595. [8] ZDUNEK R, PHAN A H, CICHOCKI A. Image classification with nonnegative matrix factorization based on spectral projected gradient [J]. Artificial Neural Networks, 2015, 4: 31-50. [9] JI Z, PANG Y, LI X. Relevance preserving projection and ranking based on one-class classification for Web image [J]. IEEE Transactions on Image Processing, 2015, 24(11): 4137-4147. [10] 汪金涛,曹玉东,孙福明.稀疏约束图正则非负矩阵分解的增量学习算法[J].计算机应用,2017,37(4):1071-1074.(WANG J T, CAO Y D, SUN F M. Incremental learning algorithm based on graph regularized non-negative matrix factorization with sparseness constraints [J]. Journal of Computer Applications, 2017, 37(4): 1071-1074.) [11] JIA X, SUN F M, LI H J, et al. Image multi-label annotation based on supervised nonnegative matrix factorization with new matching measurement [J]. Neurocomputing, 2017, 219(C): 518-525. [12] LIU H, WU Z, CAI D, et al. Constrained nonnegative matrix factorization for image representation [J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2012, 34(7): 1299-1311. [13] CAI D, HE X, HAN J, et al. Graph regularized nonnegative matrix factorization for data representation [J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2011, 33(8): 1548-1560. [14] LIU Q. Kernel local sparse representation based classifier [J]. Neural Processing Letters, 2016, 60(1): 1684-1695. [15] YIN Y L, LIU L L, SUN X W. SDUMLA-HMT: a multimodal biometric database [C]// Proceedings of the 6th Chinese Conference on Biometric Recognition. Beijing: [s.n.], 2011: 260-268. [16] CHUA T S, TANG J, HONG R, et al. NUSWIDE: a real-world Web image database from National University of Singapore [C]// Proceedings of the 2009 ACM International Conference on Image and Video Retrieval. New York: ACM, 2009: 48. [17] 苑玮琦,王爇,孙书会.基于2DFLD的手背静脉识别算法[J].计算机应用,2010,30(3):646-649.(YUAN W Q, WANG R, SUN S H. Palm-dorsa vein recognition based on two-dimensional Fisher linear discriminant [J]. Journal of Computer Applications, 2010, 30(3): 646-649.) [18] 胡学考,孙福明,李豪杰.基于稀疏约束的半监督非负矩阵分解算法[J].计算机科学,2015,42(7):280-284.(HU X K, SUN F M, LI H J. Constrained nonnegative matrix factorization with sparseness for image representation [J]. Computer Science, 2015, 42(7): 280-284.) This work is partially supported by the National Natural Science Foundation of China (61502216, 61572244). JIAXu, born in 1983, Ph. D., associate professor. His research interests include pattern recognition, machine learning. SUNFuming, born in 1972, Ph. D., professor. His research interests include multimedia processing, machine learning. LIHaojie, born in 1973, Ph. D., professor. His research interests include multimedia processing, computer vision. CAOYudong, born in 1971, Ph. D., associate professor. His research interests include pattern recognition, image processing.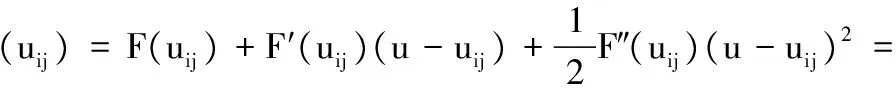
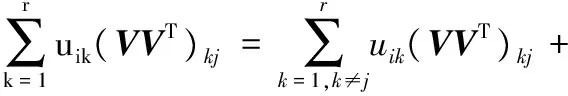
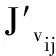

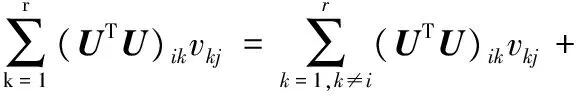
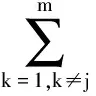
4 实验结果及分析
4.1 实验样本库及实验环境
4.2 参数设定
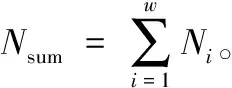
4.3 方法比较及分析
5 结语
