基于残差神经网络的图像超分辨率改进算法

王一宁，秦品乐，李传朋，崔雨豪

(中北大学 大数据学院，太原 030051)(*通信作者电子邮箱qpl@nuc.edu.cn)

0 引言

在成像、传输、转换、存储等过程中往往由于受到成像设备、外部环境等不利因素的影响使得人们获取到的图像通常是降质图像。降质意味着图像中有用信息的丢失，图像超分辨率(Super Resolution， SR)技术将低分辨率(Low Resolution, LR)图像重建出高分辨率(High Resolution, HR)图像，在医学成像、卫星成像、面部识别和监视[1-5]等领域有着广泛的应用。

目前图像超分辨率方法大致可分为3种：1)基于插值的方法。如最近邻插值(bilinear)[6]和双三次插值法(bicubic)[7]。最近邻插值法由于插值规律过于简单，易出现方块效应和边缘锯齿效应。双三次插值法比最近邻插值法运算复杂度稍高，但图像边缘的平滑度得到了提升。这两种方法的共同优点是算法简单易于实现而且运算速度快，缺点是仅仅用到局部的像素点计算得到插值点的像素值，因此无法修复图像的高频细节，得到的超分辨率图像清晰度有限。2)基于重建的方法。该类方法又分为频域法和空域法两大类。频域法通常通过消除频谱混叠现象以提升图像的分辨率，但可用到的先验知识有限。空域法具有很强的空域先验约束的能力，比较代表性的是凸集投影法(Projection Onto Convex Set, POCS)[8]、迭代反投影法(Iterative Back Projection, IBP)、最大后验概率估计法(Maximum A Posterior, MAP)、混合MAP/POCS法等。3)基于学习的方法，是近年来研究的热点。它通过学习大量的高分辨率图像得到学习模型，然后对低分辨率图像进行重建时，通过将模型中的先验知识充分结合到低分辨率图像上，从而得到具有丰富高频信息的重建图像。在现有的基于学习方法中基于邻居嵌入的方法[9-11]和稀疏表示的方法均可以得到比较好的超分辨率性能。基于邻居嵌入的单幅图像超分辨率重建(Single Image Super Resolution, SISR)方法通过使用HR图像块和LR图像块之间的几何相似度来了解它们之间的回归或映射关系。在基于稀疏表示的SISR方法中，利用稀疏编码理论将LR图像块和对应的HR图像块分别表示为相应的词典，通过机器学习方法建立词典之间的映射关系，利用学习的映射关系生成给定的单帧图像的HR图像。模型的建立和训练集合的选取是基于学习的超分辨率重建算法的核心问题。Yang等[12-13]假设输入的低分辨率图像块可以由训练样本集稀疏线性表达。Wang等[14]提出从训练样本集中学习得到一个更有效的过完备字典，适用于快速多级超分辨率图像重建任务。近年来，深度学习在图像处理领域取得了显著的研究成果。在大量的任务中，深度学习得到的特征被证实比传统方法构造的特征具有更强的表征能力[15]。Dong等[16]提出了基于卷积神经网络的图像超分辨率(Super Resolution using Convolutional Neural Network， SRCNN)算法，并将该算法应用到图像超分辨率重建领域中。此网络结构简单，超分辨率重建效果优良，但它的卷积核尺寸较大且使用了传统的双三次插值进行上采样，这些结构特点严重影响了网络的运行速度。随后，Dong等[17]又在SRCNN的基础上提出了加速的超分辨率卷积神经网络(Fast Super Resolution Convolutional Neural Network， FSRCNN)，FSRCNN结构相对比SRCNN层数加深，而且用反卷积代替了双三次插值。FSRCNN比SRCNN速度上有了很大的提升，图像的超分辨率效果也有了改进，FSRCNN在图像的超分辨率重建中取得了成功。

单图超分辨率重建任务是一个固有的病态问题，因为一个低分辨率图像有可能对应着多种高分辨率的图像。对于更大的超分辨率倍数(×4)，LR图像可能丢失大量的高频细节，因此本文在FSRCNN的基础上提出了一种新的基于残差和跳层网络的多任务损失图像超分辨率算法。整个模型分为两个阶段：第一阶段是2倍超分辨率的学习；第二阶段是4倍超分辨率图像的学习。第一阶段与第二阶段皆使用残差层和跳层结构预测出高分辨率空间的纹理信息，由反卷积层分别重建出2倍与4倍大小的超分辨率图像，并分别与相同大小的原图像作像素损失。残差层与跳层结构结合主要具有两个优点。首先，让特征直接传递到下层，从而优化梯度消失问题，使网络更容易提升训练的性能。其次，残差层能比普通堆叠卷积能更好地学习图像的边缘信息与纹理信息，这有益于构建超分辨率图像。同时，多任务损失不仅提高了网络的训练速度，而且确保了4倍超分辨率的过程中学习的准确性。2倍超分辨率输出与原图作损失调整参数，确保了网络使用反卷积将图像提升为2倍时的准确性；再使用经过调整过的网络参数继续学习4倍的超分辨率重建过程，第一阶段的2倍超分辨率学习对第二阶段的重建起到了指导的作用。该算法以任意大小的彩色图像作为输入，使用残差层和跳层结构来预测出高分辨率空间的纹理信息，并以多任务损失加强网络学习中的监督指导。实验结果显示，本文网络结果与最近邻插值、双三次插值、SRCNN和FSRCNN超分辨率重建算法相比，视觉和定量评价方面都取得了更优的结果。

1 相关理论

1.1 SRCNN算法

SRCNN是一种基于学习的SISR算法。该算法使用卷积神经网络直接学习低分辨率图像到高分辨率图像的映射关系。SRCNN的网络结构(如图1)包含三层：第一层用9×9的卷积核提取图像块的特征；第二层用1×1的卷积核作非线性映射；第三层用5×5的卷积核作HR图像块的重组。

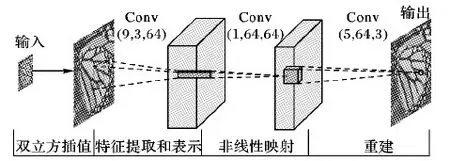
图1 SRCNN结构

SRCNN使用的是3层神经网络模型对图像的3通道进行端到端的超分辨率重建。训练过程是将91图像取步长为14的碎片，将碎片下采样到所需比例大小输入网络。网络先将输入的图像进行双三次插值将图像上采样到目标大小，再对图像进行三层卷积细化特征，卷积核大小分别是9×9、1×1、5×5，通道数依次是3到64、64到32、32到3，每个卷积层的padding参数都为0，基于卷积后得到Output图像与原图构造均方差(Mean Square Error, MSE)损失函数，以优化参数。训练用到的数据集有两个：一个是91张图片，一个是ImageNet。使用ImageNet训练的网络要比91张训练的效果更好。

此网络有两个不足之处：第一是网络的层次结构太浅，不能提取到图片更深层次的语义特征；第二是用了传统的双三次插值进行上采样，双三次插值上采样本身就有不确定性，而且运行起来速度也较慢，在后期已经逐渐被反卷积以及其他卷积方法来替代。

1.2 FSRCNN算法

FSRCNN也是基于学习的SISR算法。FSRCNN针对SRCNN作出了改进，结构相对比SRCNN层数加深，而且用反卷积代替了双三次插值。不仅效果超越了SRCNN，速度上更是有了很大的提升。FSRCNN的网络结构(如图2)包含8层：第1层用5×5的卷积核来提取图像块的特征；第2层用1×1的卷积核将特征图的数量收缩；第3～6层用3×3的卷积核作非线性映射；第7层用1×1的卷积核再将特征图扩展变大；第8层用9×9反卷积将LR图像块上采样到HR图像块，并将HR图像块重组。

训练过程是首先将91幅训练图像进行缩放、旋转并以步长12取碎片，再按照所需的比例下采样。将得到的LR图像输入8层卷积神经网络，最后在原图与输出的HR图像间作MSE损失。

此网络的不足之处：网络层数仍然较浅，很难提取到图片更深层次的语义信息；仅使用一个反卷积层重建HR图像，不适合大倍数(4倍)的图像超分辨率重建。

2 多阶段级联残差卷积神经网络

2.1 改进思想

影响网络效果的两个重要因素是网络的宽度和深度。SRCNN和FSRCNN的共性是网络架构不够深，一个是3层网络，一个是8层网络，本文基于这两点对SRCNN和FSRCNN进行了改进。考虑到过深的网络结构虽然可以将图片的特征得到更好的拟合，学习到更高层次的纹理信息，但同时也可能由于层数的过多而带来梯度弥散、特征丢失等问题。基于此类问题，本文选择了残差块和跳层结构来进行改善，使网络更快更好地达到收敛。同时，本文提出了在残差和跳层结构的基础上加入多任务损失进行调节网络参数，从而提高网络训练时的收敛速度，并进一步提高网络的精确度。最终本文提出了38层的基于残差卷积神经网络的多阶段级联超分辨率改进算法。

图2 FSRCNN结构

2.2 网络结构

多阶段残差卷积神经网络(Multi-section Cascade Residual Convolution Neural Network, MCRCNN)的设计充分考虑降质图像与超分辨率图像的关系，即网络实际是一种由降质图像到超分辨率图像的非线性映射关系。图3是本文构建的一种多阶段级联残差网络，主要分为两个子网路MULTI_A和MULTI_B，如图4～5所示。3通道的LR输入图像从输入层输入网络，先通过5×5的卷积核Conv1_1使通道数增加到64个，然后输入到MULTI_A子网络。一方面通过3×3的Conv2_2输出一个宽高皆为输入图像2倍大小的二维超分辨率图像(3通道)，计算像素损失；另一方面通过5×5大小的Conv4_1、MULTI_B得到宽高皆为输入图像4倍大小的2维超分辨率图像(3通道)。其中2倍的输出图像会和原始的图像作损失以此来调节以及指导4倍超分辨率图像的输出，因此本文的网络是将LR图像分阶段进行超分辨率重建的。

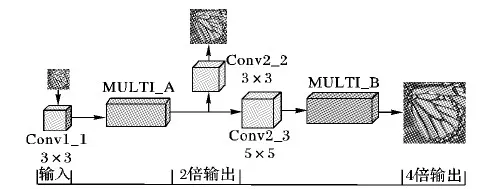
图3 多阶段级联残差卷积神经网络结构

MCRCNN输入为24×24的3通道图像，进入MULTI_A子网络(如图4)后，使用Conv2_1、Residual Block、BN2_1、DeConv2_1作为2倍超分辨率重建的特征层。图像使用5×5的卷积核Conv1对图像进行卷积，步长为1，padding为2，增加特征图数量到64个大小24×24的特征图。Residual Block由Conv、批量正则化层(Batch Normalization Layer, BN)、ReLU、Conv、BN组成，残差块中的Conv大小都是3×3，步长为1，padding为2，经过10个残差块输出64个24×24的特征图，此时特征图中的语义信息更加丰富。Conv2_1为3×3，步长为1，padding为2，输出64个24×24的特征图。Conv2_1到BN2_1的跳层连接是64个特征图的相加，这样就解决了经过残差块图像部分原始特征丢失的问题。使用大小为9×9的转置卷积DeConv2_1对图像进行上采样，步长为1，特征图增加到256个48×48的特征图。最后通过3×3大小的Conv2_2，步长为1，padding为2，输出1个48×48的3通道升2倍HR图像。

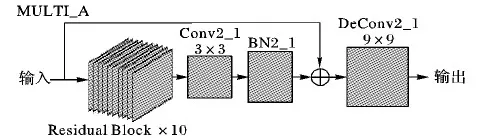
图4 MULTI_A结构

MULTI_B(如图5)与MULTI_A网络架构几乎一致，包含卷积层、6个残差块、跳层结构以及反卷积结构。MULTI_A中进行Deconv2_1后的256个48×48的特征图输入到5×5大小的Conv4_1,，步长为1，padding为2，输出64个48×48的特征图，接着输入到MULTI_B中，经过6个Residual Block输出64个48×48的特征图，再输入到3×3大小的Conv4_2，步长为1，padding为2，输出64个48×48的特征图。最后使用9×9大小的转置卷积DeConv4_1对图像进行上采样，步长为1，输出1个96×96的3通道HR图像。

图5 MULTI_B结构

由于本文所提出的结构较深，低层的特征图与高层的特征图之间特征分布差异较大，使用跳层结构直接将低层特征与高层特征融合会造成网络难以学习，因此本文在残差块以及跳层结构中加入了BN[18]对数据作归一化操作。在BN层后，使用具有单侧抑制且稀疏激活的ReLU[19]激活函数来提高网络的非线性建模能力。

2.3 残差和跳层

本文网络设计的灵感来自He等[20]和Johnson等[21]。He等[20]提出了152层的ResNet网络，其不仅在层数上面创下记录，在ImageNet数据集上也将top5错误率降低到了3.6%。残差网络近来已被证明在许多图像生成任务中取得优异的成果。残差结构是在标准的前馈卷积网络上加一个跳跃绕过一些层的连接，每绕过一层就产生一个残差块(Residual Block)。

训练非常深的网络，残差块比堆叠卷积-BN-ReLU更有利于收敛。普通的深度前馈网络难以优化，网络结构的加深使得训练和验证的错误率增加，即使用了BN也是如此。残差神经网络由于存在快捷连接，网络间的数据传输更为顺畅，也改善了因梯度消失而形成的欠拟合现象。虽然组成本文网络的主要部分的残差块仅仅负责添加残差信息，但是此结构有助于在训练期间使训练更加稳定并减少输出中的颜色偏移。本文的每个残差块包含两个3×3的卷积层，3×3的使用是受VGG架构[22]的启发。残差块的定义如图6所示。

图6 残差块

y=F(x)+x

(1)

其中：x和y分别表示残差块的输入和输出向量；函数F(x)表示残差映射。本文的残差块中除了卷积层，还有BN层和ReLU层。BN层用来对某一个层网络的输入数据进行归一化处理，也就是使得每一维特征均值为0，标准差为1，如式(2)所示：

(2)

其中：E[x(k)]指每一批训练数据神经元x(k)的平均值；分母是每一批数据神经元x(k)的标准差，但此公式仅对网络某层的输出数据作归一化，会影响到本层网络所学习到的特征，强制把本层的数据归一化处理，标准差也限制在1，破坏掉了本层网络学习到的特征。于是引入可学习参数γ、β，如式(3)所示：

(3)

修正线性单元ReLU有单侧抑制和稀疏激活性，数学表达式如(4)所示。把BN放在激活函数之前，这是因为wx+b具有更加一致和非稀疏的分布。

f(x)=max(0,x)

(4)

同样跳层结构也已经被研究了很长的时间。在训练多层感知器(Multi-Layer Perceptron， MLP)网络的早期实践中，跳层从网络的输入直接连到输出[23]。后来，一些中间的层被直接连到附加的网络层来解决梯度消失或者梯度爆炸问题[24]。在文献[25-26]中也都用到了跳层结构来解决梯度和传播误差。本文的跳层结构有两个，分别是MULTI_A中由输入连接到BN2_1和MULTI_A中由输入连接到BN4_1，解决了图像经过残差块学习后部分原始特征丢失的问题。

本文网络就是残差结构和跳层结构结合的一个全新的网络。训练样本和LR图像包含类似的信息，本文通过残差结构学习出训练样本图像中的高频信息，然后通过跳层结构将残差结构学到的高频信息与LR图像的原始信息进行叠加，最后以反卷积重建出HR图像。

2.4 多任务损失

网络结构由两部分组成：一部分是MULTI_A负责2倍HR图像的特征提取；一部分是MULTI_B负责4倍HR图像的特征提取。综合考虑2倍超分辨率图像和4倍超分辨率图像重建的均方差，构建多任务损失函数,如式(5)～(7):

LMCR=min[LS1(S1(PLR),PHR2)+

LS2(S2(S1(PLR)),PHR4)]

(5)

(6)

S2(S1(PLR(i,j))))2)

(7)

其中：PLR为网络的输入图像；S1(PHR2)为图像经过Conv2_2后训练输出的2倍HR图像；S2(S1(PHR))为经过MULTI_B训练输出的4倍HR图像；PHR2、PHR4为供参考的2、4倍原始高清图像；PHR2(i,j)-S1(PLR(i,j))和PHR4(i,j)-S2(S1(PLR(i,j)))都表示残差；LS1表示S1(PHR2)与PHR2像素之间的损失；LS2表示S2(S1(PHR))与PHR4像素之间的损失；n表示每个训练批次的样本数，本文n=16，H、W分别为图像的高度和宽度。网络训练的目标是最小化均方差损失函数。

SRCNN和FSRCNN都是在网络的最后一层作一次损失，属于单任务损失。经过实验Multi-Section-Residual与FSRCNN-Residual的对比，验证了子网络、反卷积1、子网络、反卷积2的多阶段学习提升超分辨率效果比子网络、反卷积1、反卷积2的单阶段学习好。而在MULTI_A末尾和MULTI_B末尾一起或分别作损失比仅在网络最后作一次损失来更迭参数能取得更好的效果。任意选取实验Multi-Section-Residual中网络结构对应本文MCRCNN-together结构中MULTI_A中的DeConv1输出的6张特征图与本文MCRCNN-together网络的DeConv1输出的6张特征图的对比如图7所示。图7(a)～(f)为实验Multi-Section-Residual中DeConv1输出的随机的6张特征图，图7(g)～(l)为实验MCRCNN-together的DeConv1输出的随机的6张特征图(91张图片作为数据集)。

显然本文多任务损失结构下DeConv1输出得到的特征图纹理细节、图像的亮度信息以及语义信息更加丰富，相当于在网络的训练过程中加了约束项，从而有效地指导了在4倍超分辨率的过程中网络的学习训练情况。

除此之外，多任务损失可以大幅度提高网络的训练速度。相同的网络结构用两个损失函数同时对网络进行参数的调节，使得网络训练时可以提升接近一倍的速度，大幅度提高了网络的学习效率。

2.5 评价标准

本文选择用公共数据集Set5[27]、Set14[28]进行测试，并选用峰值信噪比(Peak Signal-to-Noise Ratio, PSNR)和平均结构相似性(Mean Structural SIMilarity, MSSIM)作为图像质量的参考评价指标。PSNR如式(8)所示，指的是基于像素点之间的误差，是基于误差敏感的图像质量评价。n为每像素的比特数，本文用的RGB通道，所以n取8，即像素的灰阶数为256。PSNR单位为dB，数值越大失真越小。

PSNR=10 lg ((2n-1)2/MSE)

(8)

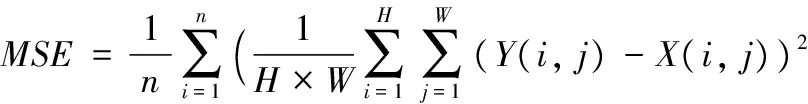
SSIM分别从亮度、对比度、结构三方面来衡量图像结构的完整性，取值范围为[0,1]，值越大表示图像的失真效果越小。

SSIM(X,Y)=l(X,Y)·c(X,Y)·s(X,Y)

(9)

(10)

(11)

(12)

其中：X为降质图像经过网络训练输出的超分辨率图像；Y为供参考的原始高清图像；μX、μY分别表示图像X、Y的均值；σX、σY分别表示图像X和Y的方差；σXY表示图像X、Y的协方差。

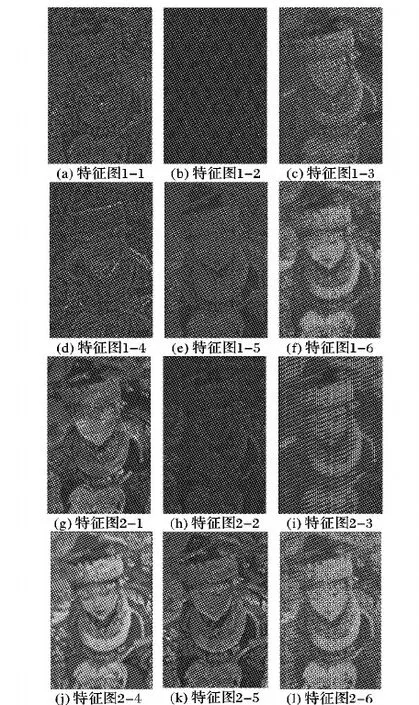
图7 特征图对比

(13)

(14)

μY))

(15)

其中：C1、C2、C3为常数，为了避免分母为0的情况，通常取C1=(K1×L)2，C2=(K2×L)2，C3=C2/2，一般地K1=0.01，K2=0.02，L=255。MSSIM如式(16)所示：

(16)

其中：N表示N张图片，使用Set5测试时，N=5；使用Set14测试时，N=14。

3 实验与结果分析

3.1 数据集预处理

训练数据集：为验证本文所提MCRCNN算法的有效性，本文将在91张数据集和ILSVRC 2014 ImageNet数据集[16]上训练网络模型，并与SRCNN、FSRCNN及其他超分辨率方法进行对比分析。

91张数据集被广泛用作基于学习的SR方法的训练集[16-17]。由于深度模型通常受益于大数据，而91张图像不足以将深度模型推向最佳性能。为了充分利用数据集，本文采用了数据扩增。本文以两种方式增加数据：1)比例缩放。每张图像都分别按照0.9,0.8,0.7和0.6的比例进行缩放。2)旋转。每张图像旋转90°，180°和270°，以此获得了5×4-1=19倍的图像进行训练。制作数据集时，首先对原始训练图像采用高斯滤波(δ=1.5)和双立方插值下采样4倍来得到LR图像，然后以步长12将LR训练图像裁剪成一组96×96像素子图像，最后得到72 118张图像。相应地，HR子图像也从原图像中剪切出来。对于×2和×4，本文将LR/HR子图像的大小分别设置为24/48和24/96，这些LR/HR子图像对就是用来作为训练的数据。在卷积需进行填充时，由于填充与否对输入或输出映射对最终性能影响不大，因此，本文根据滤波器尺寸在所有层中采用0进行填充，以此来使网络训练出的图片是真正地提升了4倍大小，从24×24提升到96×96。对于网络中参数的初始化，都是从零均值和标准偏差0.001的高斯分布中随机绘制生成，网络的初始学习速率初始设置为10-4，采用Adam优化方法来使网络可以在确定范围内自动调节学习率，使得参数学习比较平稳，无dropout，运用Mini-batch训练方式batch-size=16，训练了10万次。

考虑到本文网络的层数较深，使用91张数据集在训练过程中易出现过拟合，于是针对本文提出的一系列网络实验模型使用了数据量为127万的ILSVRC 2014 ImageNets数据集进行了第二次训练。由于127万数据过于庞大，于是每间隔两张图片取一张，直到取到105万张时终止，从而获取了35万张的图片，并将获取到的图片统一压缩为256×256的图像进行保存。最后将256×256的图像都以随机位置取96×96的碎片，得到本文需要的原图HR标签。制作24×24的LR标签时，对96×96的原图像采用高斯滤波(δ=1.5)和AREA下采样2倍和4倍来得到LR图像，以此组成了24/48和24/96的LR/HR图像对，其余与91张训练训练集的制作相同。

3.2 实验设计

为验证本文提出的多阶段级联残差卷积神经网络结构的正确性及有效性，本文设计如下5个实验(如表1)。

图8 MCRCNN-fast结构

1) FSRCNN-Residual。按照FSRCNN的网络结构，第一层仍用5×5的卷积提取特征，将最后一层反卷积换成两层9×9和9×9的反卷积进行上采样操作，中间的层将普通堆叠卷积换成了16个残差块(图3)与跳层结合的结构。本实验会与FSRCNN进行对比，以此验证残差块+跳层结构的有效性。

2)Multi-Section-Residual。将实验1)中的连续进行两次的反卷积上采样改为第一次反卷积前采用10层残差层+跳层结构，第二次反卷积前同样通过6层残差块+跳层结构来学习细化纹理特征，增强了模型的拟合能力。本实验为多阶段的网络，第一次反卷积重建为2倍HR图像，第二次反卷积重建为4倍HR图像。本实验会与实验1)进行对比，验证多阶段级联残差网络提取特征的有效性。

3)MCRCNN-apart。本实验与实验2)进行对比，验证多任务损失的有效性。

4)MCRCNN-together。本实验与实验3)的差异就是损失的调参不同，与实验3)在图片效果与训练速度上进行对比。

5)MCRCNN-fast。为了提高MCRCNN-together的运行速度，实时地输出4倍HR图像，选用了网络层数更少的单任务损失以及较小的卷积核和反卷积核。网络结构如图8所示。

3.3 实验结果分析

为了验证本文所提出的基于残差神经网络的图像超分辨率改进算法的有效性，本文分别使用处理过的91张图片数据集和ImageNet数据集[16]统一对各网络结构进行4倍的超分辨率训练，网络模型的迭代次数都为10万次。选用公共测试集Set5[25]和Set14[26]进行仿真实验，以平均PSNR、MSSIM以及平均耗时的方式比较各网络模型对超分辨率的效果，并将本文网络的超分辨率结果与现有的性能优越的算法进行对比。首先，本文的算法与传统的bilinear、bicubic进行比较，接着与2种基于学习SR算法进行比较，即SRCNN、FSRCNN。这些方法都是基于bilinear、bicubic、SRCNN和FSRCNN模型，在GPU为NVIDIA Tesla M40，Tensorflow V1.01的实验环境下运用Python3.5进行仿真的结果。由于与提出SRCNN和FSRCNN模型的原论文[16-17]的实验环境以及训练迭代次数的不同，实验结果与原论文会略有不同，但仍能反映主要的趋势。91张图片训练出来的模型测试结果如图9所示，实验测试指标如表2所示。图9中，图(a)～(d)第一行从左到右依次为4种经典模型的4倍超分辨率效果图，图(e)～(i)都是本文的实验测试结果，图(j)为原图。

表1 本文提出的实验模型

PSNR和SSIM作为评价超分辨率质量的传统指标，两者仅依赖于像素间低层次的差别，不能完全代表人类的视觉质量(文献[27]同样提出了这种观点)，所以本文在使用PSNR和SSIM作为评价标准的前提下，综合使用肉眼来感官上判别一张图像质量的好坏。表2中，虽然本文网络的评价指标并不高，但从肉眼感官可判断，图9(f)、(g)、(h)、(i)的蝴蝶放大后的细节中，蝴蝶纹理的边缘更加清晰和平滑。本文的网络的质量明显优于nearest、bicubic、SRCNN和FSRCNN。

由表2可看出，FSRCNN-Residual精度高于FSRCNN，验证了对于本文的较深层的网络，残差块和跳层结构比堆叠卷积更适合，因为16层残差网络更深而且与跳层结构结合，可以学到更深高层次的纹理信息。同时Multi-Section-Residual精度高于FSRCNN-Residual，先将LR图像通过反卷积提升到2倍，再将2倍HR图像进行特征提取，最后进行反卷积升到4倍HR，验证了分阶段提升分辨率比一次性提升更合适。MCRCNN-apart精度高于Multi-Section-Residual，验证了多任务损失中2倍超分辨率作损失确实对4倍的超分辨率过程有指导意义，效果优于单任务损失。MCRCN-together精度与MCRCNN-apart不相上下，但MCRCN-together训练模型时的速度却远高于MCRCNN-apart。所以综合考虑后，本文选择MCRCNN-together作为本文的最终结构。最后为了提高本文网络的速度，提出了MCRCNN-fast网络。跳层连接用了卷积核大小为1×1、3×3、1×1的结构，1×1的使用可以提高网络的运行速度。尤其在MCRCNN2-fast网络模型中，使用了2个3×3的反卷积代替了FSRCNN中的9×9的1个反卷积，这样大幅度提高了整个网络的速度，虽然精度略逊色于MCRCNN，但在精度与速度上达到了一个平衡。

图9 各方法对比图1(Butterfly)

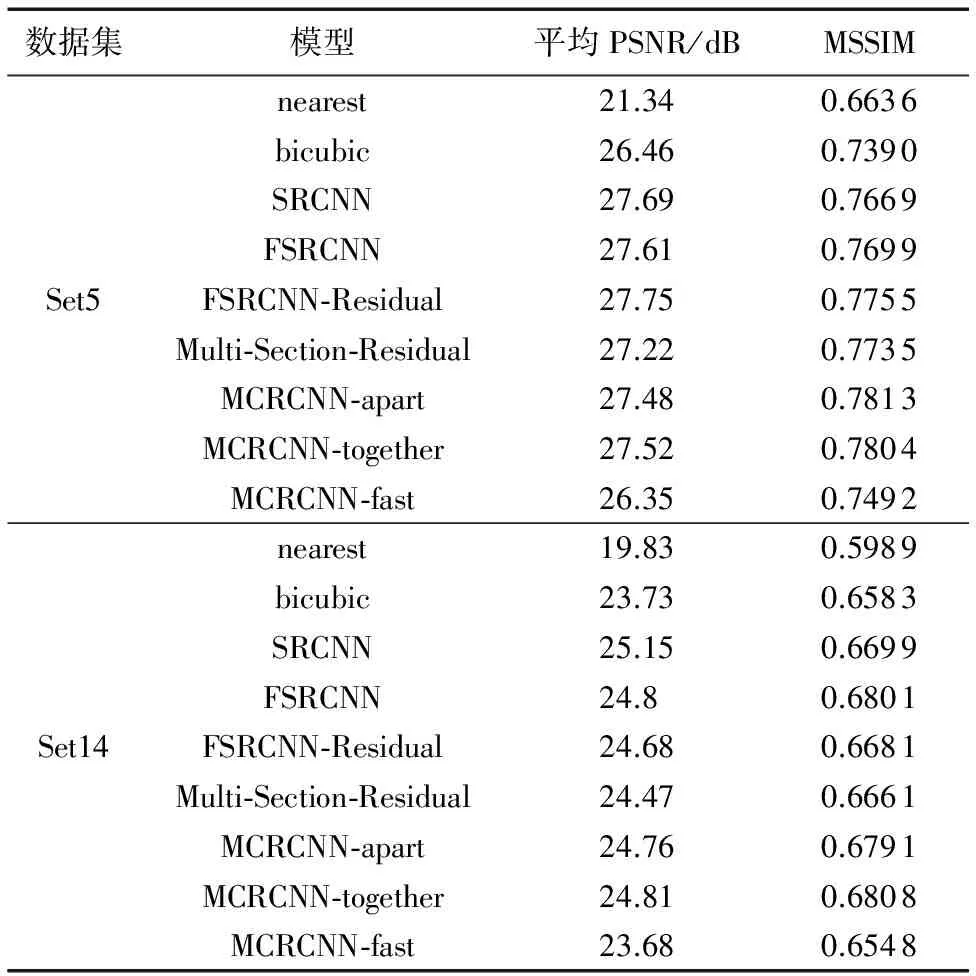
表2 各实验模型在两个数据集上的超分辨率结果对比(用91张图片数据集训练)

由于本文网络架构较深，所以使用ImageNet数据集训练MCRCNN会达到更好的效果。由于FSRCNN原网络中并没有使用ImageNet作为训练集，此处仅与nearest、bicubic、SRCNN进行对比，测试结果如图10所示，实验测试指标如表3所示。图10中，图(a)～(c)为3种经典模型的4倍超分辨率效果图，图(d)～(g)都是本文的实验测试结果，图(h)为原图。

从表3可以看出：SRCNN在Set5与Set14上平均PSNR分别为28.50和25.72，MSSIM分别为0.784 1和0.692 9；而本文的MCRCNN-together平均PSNR达到了29.95和26.78，MSSIM分别为0.817 6和0.722 8。从图11可以明显看出，图中越靠近左上方位置的模型耗时越短、精度越高。本文提出的MCRCNN在图像分辨率精确度上优于nearest、bicubic以及SRCNN这几种有代表性的超分辨率方法，MCRCNN-fast更是从速度和精确度上都优于SRCNN。

表3 各实验模型在两种数据集上的超分辨率结果对比(用ImageNet数据集训练)

相比较于其他的方法，本文用特征重建训练的模型得到了很好的×4倍超分辨率重建的结果，尤其是在锋锐的边缘和纹理很丰富的图像区域，比如图9中每张图片左下角中展示的放大的蝴蝶纹理细节以及图10中小女孩的眼睛睫毛细节。

4 结语

本文提出了一种基于残差神经网络的图像超分辨率改进算法，该网络由输入层、卷积子网、残差子网络、跳层子网络、反卷积子网和输出层构成。输入层直接将二维的低分辨率图像输入到神经网络，卷积子网、残差子网络、跳层子网络负责学习提取出更多的特征，反卷积子网负责整合图像特征从而重建超分辨率图像信息，并由输出层输出HR图像，整个网络构成了一种由LR图像到HR图像的非线性映射。

图10 各方法对比图2(Comic)

图11 各实验模型超分辨率结果对比

通过实验对比，本文的网络模型对纹理的细节有较大的提升，并且本文还提出了一个运行速度与精度都不低于FSRCNN的网络MULTI-fast，充分说明了本文改进方法的有效性。在未来的工作中，将寻求更好的优化策略，尝试扩展网络结构的宽度，进一步提高超分辨率图像重建的精度；同时，医学图像的超分辨率重建也将是下一步的研究方向。

References)

[1] PELED S, YESHURUN Y. Superresolution in MRI: application to human white matter fiber tract visualization by diffusion tensor imaging [J]. Magnetic Resonance in Medicine Official Journal of the Society of Magnetic Resonance in Medicine, 2001, 45(1): 29.

[2] SHI W, CABALLERO J, LEDIG C, et al. Cardiac image super-resolution with global correspondence using multi-atlas patchmatch [C]// MICCAI 2013: Proceedings of the 2013 International Conference on Medical Image Computing and Computer-Assisted Intervention. Berlin: Springer, 2013: 9-16.

[3] THORNTON M W, ATKINSON P M, HOLLAND D A. Sub-pixel mapping of rural land cover objects from fine spatial resolution satellite sensor imagery using super‐resolution pixel-swapping [J]. International Journal of Remote Sensing, 2006, 27(3): 473-491.

[4] GUNTURK B K, BATUR A U, ALTUNBASAK Y, et al. Eigenface-domain super-resolution for face recognition [J]. IEEE Transactions on Image Processing, 2003, 12(5): 597-606.

[5] ZHANG L, ZHANG H, SHEN H, et al. A super-resolution reconstruction algorithm for surveillance images [J]. Signal Processing, 2010, 90(3): 848-859.

[6] 苏衡,周杰,张志浩.超分辨率图像重建方法综述[J].自动化学报,2013,39(8):1202-1213.(SU H, ZHOU J, ZHANG Z H. A summary of super-resolution image reconstruction methods [J]. Acta Automatica Sinica, 2013, 39(8): 1202-1213.)

[7] KEYS R. Cubic convolution interpolation for digital image processing [J]. IEEE Transactions on Acoustics Speech & Signal Processing, 1981, 29(6): 1153-1160.

[8] 袁琪,荆树旭.改进的序列图像超分辨率重建方法[J].计算机应用,2009,29(12):3310-3313.(YUAN Q, JIN S X. Improved sequence image super-resolution reconstruction method [J]. Journal of Computer Applications, 2009, 29(12): 3310-3313.)

[9] TIMOFTE R, DE V, GOOL L V. Anchored neighborhood regression for fast example-based super-resolution [C]// Proceedings of the 2013 IEEE International Conference on Computer Vision. Piscataway, NJ： IEEE, 2013: 1920-1927.

[10] TIMOFTE R, SMET V D, GOOL L V. A+: adjusted anchored neighborhood regression for fast super-resolution [C]// Proceedings of the 2014 Asian Conference on Computer Vision. Berlin: Springer, 2014: 111-126.

[11] YANG C Y, YANG M H. Fast direct super-resolution by simple functions [C]// Proceedings of the 2013 IEEE International Conference on Computer Vision. Washington, DC: IEEE Computer Society, 2013: 561-568.

[12] YANG J, WRIGHT J, HUANG T, et al. Image super-resolution as sparse representation of raw image patches [C]// CVPR 2008: Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition. Washington, DC: IEEE Computer Society, 2008: 1-8.

[13] YANG J, WRIGHT J, HUANG T S, et al. Image super-resolution via sparse representation [J]. IEEE Transactions on Image Processing, 2010, 19(11): 2861-2873.

[14] WANG J, ZHU S, GONG Y. Resolution enhancement based on learning the sparse association of image patches [J]. Pattern Recognition Letters, 2010, 31(1): 1-10.

[15] KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks [C]// Proceedings of the 2012 International Conference on Neural Information Processing Systems. West Chester, OH: Curran Associates Inc., 2012: 1097-1105.

[16] DONG C, CHEN C L, HE K, et al. Learning a deep convolutional network for image super-resolution [C]// ECCV 2014: Proceedings of the 2014 European Conference on Computer Vision. Berlin: Springer, 2014: 184-199.

[17] DONG C, CHEN C L, TANG X. Accelerating the super-resolution convolutional neural network [C]// ECCV 2016: Proceedings of the 2016 European Conference on Computer Vision. Berlin: Springer, 2016: 391-407.

[18] SUN J, SHUM H Y. Image super-resolution using gradient profile prior: US9064476 [P]. 2015- 06- 23.

[19] NAIR V, HINTON G E. Rectified linear units improve restricted boltzmann machines [C]// Proceedings of the 2010 International Conference on International Conference on Machine Learning. Madison, WI: Omnipress, 2010: 807-814.

[20] HE K, ZHANG X, REN S, et al. Deep residual learning for image recognition [C]// CVPR 2016: Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Washington, DC: IEEE Computer Society, 2016: 770-778.

[21] JOHNSON J, ALAHI A, LI F F. Perceptual losses for real-time style transfer and super-resolution [C]// Proceedings of the 2016 European Conference on Computer Vision. Berlin: Springer, 2016: 694-711.

[22] SIMONYAN K, ZISSERMAN A. Very deep convolutional networks for large-scale image recognition [EB/OL]. [2017- 03- 21]. https://arxiv.org/abs/1409.1556.

[23] REN S, HE K, GIRSHICK R, et al. Object detection networks on convolutional feature maps [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(7): 1476-1481.

[24] SRIVASTAVA R K, GREFF K, SCHMIDHUBER J. Training very deep networks [EB/OL]. [2017- 03- 20]. https://arxiv.org/abs/1507.06228.

[25] SAXE A M, MCCLELLAND J L, GANGULI S. Exact solutions to the nonlinear dynamics of learning in deep linear neural networks [EB/OL]. [2017- 03- 12]. http://arxiv.org/abs/1312.6120.

[26] SIMONYAN K, ZISSERMAN A. Very deep convolutional networks for large-scale image recognition [EB/OL]. [2017- 03- 10]. https://arxiv.org/abs/1409.1556.

[27] BEVILACQUA M, ROUMY A, GUILLEMOT C, et al. Low-complexity single-image super-resolution based on nonnegative neighbor embedding [C]// Proceedings of the 2012 British Machine Vision Conference. [S.l.]: BMVC Press, 2012: 135- 1-135- 10.

[28] ZEYDE R, ELAD M, PROTTER M. On single image scale-up using sparse-representations [C]// Proceedings of the 2010 International Conference on Curves and Surfaces. Berlin: Springer, 2010: 711-730.

[29] JOHNSON J, ALAHI A, LI F F. Perceptual losses for real-time style transfer and super-resolution [C]// Proceedings of the 2016 European Conference on Computer Vision. Berlin: Springer, 2016: 694-711.

This work is partially supported by the Natural Science Foundation of Shanxi Province (2015011045).

WANGYining, born in 1992, M. S. candidate. Her research interests include deep learning, machine vision, digital image processing.

QINPinle, born in 1978, Ph. D., associate professor. His research interests include big data, machine vision, three-dimensional reconstruction.

LIChuanpeng, born in 1991, M. S. candidate. His research interests include deep learning, machine vision, digital image processing.

CUIYuhao, born in 1996. His research interests include deep learning, digital image processing.