基于云计算和改进K-means算法的海量用电数据分析方法
2018-03-20张承畅张华誉罗建昌
张承畅,张华誉,罗建昌,何 丰
(1.重庆邮电大学 光电工程学院,重庆 400065; 2.重庆邮电大学 通信与信息工程学院,重庆 400065)(*通信作者电子邮箱15923180953@139.com)
0 引言
近年来,随着化石能源的日益枯竭,社会对环境保护、节能减排和可持续发展的要求日益提高,未来的电网必须是“绿色”的电网,未来的小区也必须是“绿色”的小区。在此背景下,居民用电行为逐步智能化,电网和用户实现用电信息的双向交互成为必然趋势。由于智能小区在不断建设和发展过程中积累了大量的基础用电数据,这些数据不仅具有海量、高频、分散等特点,而且数据之间存在关联性和相似性[1-2]。对智能小区用户的用电数据采用大数据分析方法进行挖掘并研究用户类型,可以帮助电网公司了解用户消费习惯,为用户提供个性化、差异化的服务需求,从而帮助电网公司进一步拓展服务的深度和广度,为未来的电力需求响应政策的制定提供数据支撑。同时,电网公司将小区用电数据及居民用电情况及时反馈给用户,让用户清楚自身用电信息,规范用电行为,挖掘节能潜力,为低碳环保作贡献[3-5]。
聚类分析[6]是数据挖掘领域的一种经典方法,能够以较高的效率挖掘出海量数据中的隐含信息。聚类分析方法也逐步应用到智能电网领域。文献[7]提出了一种应用于电力系统短期负荷预测方法,采用双向比较法对电力数据预处理后,并用K-means算法对数据进行聚类分析,使具有相似特征属性的数据归为一类,达到降低数据维度的目的。文献[8]中提出基于改进K-means的电力负荷曲线聚类方法,采用了基于核方法的聚类算法实现负荷曲线的聚类分析,提高了聚类的准确率。文献[9]提出了一种基于K-means算法台区线损率计算方法,通过K-means算法对样本数据的聚类,解决数据分散的问题,从而提高了线损率计算的准确性。文献[10]中提出了一种基于优化K-means算法的电力客户划分方法,采用一种将Canopy算法与K-means算法相结合的方法,解决传统K-means的初始中心点选择的问题,提高了聚类的稳定性。然而,以上的聚类方法面对海量智能用电数据时,存在效率低、计算量大的瓶颈,无法对海量数据进行高效挖掘。
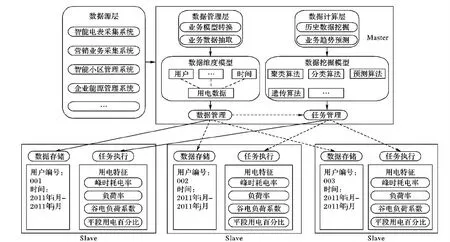
图1 基于云计算的海量用电数据分析模型架构
针对智能电网中海量数据集的存储与计算问题,相关学者利用云计算技术进行了研究与探索,并且取得了一定的成果。文献[11]提出了基于聚类算法和云计算的居民用电行为分析模型,通过K-means算法将用电行为相似的用户进行聚类,并分析出用户的特征,同时基于云计算技术实现算法的并行化,提高了聚类的效率,然而针对K-means算法中初始中心和K值的确定问题并没有给出解决方法。文献[12]中提出了一种基于云计算的智能电网数据挖掘的方法,文中针对传统K-means算法存在的初始中心和K值问题,采用Canopy算法对数据进行预聚类,并将结果作为K-means的输入参数,但Canopy算法中存在阈值T1和T2难确定的问题,并且阈值的选择对聚类结果的影响很大。
本文针对智能电网中海量用电数据的处理,提出了一种基于云计算和改进K-means算法的用电数据分析方法。通过改进的K-means算法,提高了算法聚类的准确度,并基于MapReduce模型实现其并行化,提高了算法的效率。文中以海量的用电数据为基础,通过改进的算法挖掘出数据中潜在的价值信息,实现用户用电行为的分析,从而为电网公司制定最优的用电策略提供了重要的依据。
1 海量用电数据分析模型架构
本文采用云计算主/从(Master/Slave, M/S)架构实现海量用户用电数据的存储和分布式计算[13],通过数据挖掘算法对数据进行分析,提取数据中隐含的有价值的信息。图1是基于云计算的海量用电数据分析模型架构。
基于云计算的海量用电数据分析模型架构主要由云计算主服务器(Master)和云计算从服务器(Slave)组成。数据源端将采集到的用电数据传到云计算主服务器(Master)进行数据管理和计算任务。数据管理层负责对源数据进行业务模型转换和数据抽取,建立用电数据维度模型;数据计算层负责对历史用电数据的挖掘分析和业务趋势预测,建立数据挖掘模型。云计算从服务器(Slave)根据主服务器的任务管理机制,主要负责数据存储和计算任务的执行。主服务器(Master)将接收到的用电数据经过处理后分配到各个从服务器(Slave)分布式存储,同时管理相应任务的执行,实现海量用电数据的分析,快速、高效地获取数据中有价值的信息。
2 海量用电数据分析方法
2.1 Hadoop云计算平台
Hadoop是一个使用MapReduce编程模型对大数据集进行分布式存储和处理的开源软件架构,它是一个更容易开发和并行处理大数据集的云计算平台,具有扩容能力强、成本低、效率高以及高可靠性等优点。Hadoop平台由以下两个部分组成:Hadoop分布式文件存储系统和MapReduce计算模型[14]。Hadoop分布式文件系统(Hadoop Distributed File System,HDFS)采用的是主从架构,一个HDFS集群包含一个管理节点(NameNode)和若干数据节点(DataNode),每个节点相当于一台计算机(Personal Computer,PC)。而MapReduce则完成数据的计算和高效分析任务。
2.2 改进的K-means算法
2.2.1 传统K-means算法
K-means是一种基于划分的聚类方法[15],具有简单、高效和可扩展性强的特点,在各个领域被广泛应用。K-means算法通常采用两样本间的欧氏距离作为衡量相似性的指标,其基本思想是:在数据集D中,随机选取K个初始聚类中心,计算余下样本数据到初始中心的欧氏距离,根据最小距离原则将各个样本归入到相应的聚类中心所在的类,然后计算每个类的所有样本的平均距离,并更新为该类的新的聚类中心,直到误差平方和函数稳定在最小值。
设数据集集合D={x1,x2,…,xn},xi=(xi1,xi2,…,xir),xj=(xj1,xj2,…,xjr),则样本xi与样本xj之间的欧氏距离为:
d(xi,xj)=
(1)
误差平方和函数如下:
(2)
其中:K为聚类类别数,ri为第i类中样本的个数,ni是第i类中样本的平均值。
2.2.2 对传统K-means算法的改进
传统K-means聚类算法中,是随机选取初始聚类中心,而这种随机性会对结果造成很大的影响。为了解决最佳K值的确定和初始聚类中心选择的问题,提出了一种加入密度参数的改进算法。改进算法将数据集的密度考虑到初始中心点的选取上,在样本密度更大的数据集合中选取聚类中心,相比传统K-means算法随机选取聚类中心的方法,可减少这种随机性对聚类结果带来的影响。
按照式(1)计算两个样本之间的欧氏距离d(xi,xj);
按照式(3)计算数据集D中所有样本间的平均距离MeanDis(D):
(3)
按照式(4)计算数据集中样本i的密度:
(4)
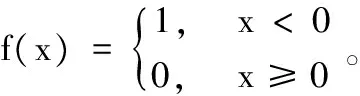
由式(4)可知,ρ(i)为满足与样本i的距离小于MeanDis(D)的样本元素数目。所有满足条件的样本元素构成一个簇,定义簇内样本的平均距离为:
(5)
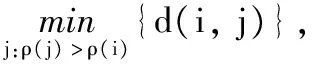
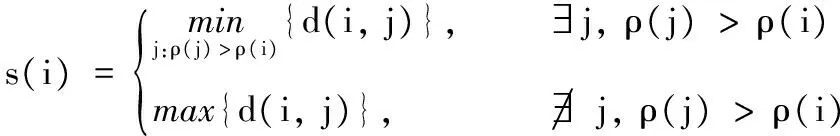
(6)
定义数据集的样本密度ρ(i)、簇内样本平均距离的倒数1/a(i)和簇间距离s(i)的乘积为权值积,即:
(7)
传统K-means算法是随机选择初始聚类中心,这种随机性会对聚类结果造成很大的影响。本文提出样本密度最大权值法,可以降低这种随机性对聚类结果造成的不稳定,同时提升准确率。最大权值积法介绍如下。
首先根据式(4)计算样本元素的密度,找出密度值最大元素作为第一个聚类中心,将所有满足式(3)中样本与初始聚类中心的距离小于MeanDis(D)条件的样本元素加入当前簇,同时将这些样本点从集合D中去除;按照式(4)~(7)计算余下元素权值积w,找出最大值,并选取对应样本元素作为第二个聚类中心,重复进行,直到集合D为空集。其中,ρ(i)越大,代表样本点i周围元素点越多,元素越集中;a(i)越小,1/a(i)越大,表示簇中元素越密集;s(i)越大,说明两簇之间距离越远,其相异度就越大。因而,通过最大权值法可以求出最佳聚类中心,同时,密度参数的引入,使得初始中心的选取更具有客观性。
2.3 基于云计算和改进K-means算法的海量用电数据分析
2.3.1 用电数据预处理
在海量的居民用电数据挖掘中,为了提高算法的执行效率,需要对数据进行预处理,如图2所示。

图2 数据预处理步骤
Fig. 2 Procedure of data preprocessing
1)数据过滤。
在原始居民用电数据中,可能存在某个用户某一时刻的用电信息数据被重复记录,或者被分成多条用电信息进行记录。针对重复记录的数据采用直接过滤删除的方法,而对于后者,可以提取出用户编号后,将用电信息进行叠加合并,整合成一条数据进行记录。此外,用户的某一条数据也可能存在若干缺失值。针对这类情况,可以事先设定一个缺失值个数阈值,当超过阈值时,直接把该条记录删除;反之,则只过滤掉该缺失值。
2)数据填充。
针对缺失值采取的处理方法是:选取缺失值的相邻两负荷值的平均值作为相应的填充值。若邻值也为空值,则相应向前或向后查找下一个非空负荷值,若不存在非空负荷值,则以0值填充。
3)特征提取。
在负荷数据中,存在一些电压值、电流值以及一些名称和时间值,这些数据对于用电分析作用不大,因而可以不予考虑。本文选用的特征包括:峰时耗电率、负荷率、谷电负荷系数以及平段用电量百分比。
①峰时耗电率。用户在高峰时段的用电量与总的用电量之间的比值。
②负荷率。用户在一定时间端内的平均负荷与最大负荷之间的比值。
③谷电负荷系数。用户在低谷时段的用电量与总的用电量之间的比值。
④平段用电量百分比。除去高峰和低谷时段之后的用电量与总的用电量之间的比值。
提取以上用电特征,对用户对象进行评价描述,并将每一个对象写成一个矩阵:X=[x1x2…xp]。
4)特征规范化。
在原始数据中,提取相关用户特征后,不同特征值可能具有不同的值域。值域较大的特征值对整体矩阵的影响将大于值域较小的特征值,从而削弱了数值小的特征的作用,因此需要对特征进行规范化处理。
文中采用的是区间规范化方法对特征值矩阵X=[x1x2…xp]进行处理,计算出特征矩阵中特征值的最大值max(xi)和最小值min(xi),根据式(8)将各个特征值值域规范化到区间[0,1],得到一组规范化的矩阵V=[v1v2…vp]。
vi=[xi-min(xi)]/[max(xi)-min(xi)]
(8)
其中vi∈[0,1],i=1,2,…,p。
采用规范化处理后得到矩阵V=[v1v2…vp],最终基于该矩阵完成居民用电数据集的聚类任务。
2.3.2 基于改进K-means算法的用电数据并行挖掘
用电信息数据集按行存储在Hadoop分布式文件系统中,并将数据集分成各个切片形成子数据集,MapReduce计算架构读取每一个切片数据完成计算任务。首先通过并行模型计算出K-means算法的输入参数:初始聚类中心和最优K值,然后将计算任务再分配给Map任务节点,完成数据集的并行聚类任务。
并行K-means的MapReduce计算任务执行步骤如下。
步骤1 对存储在分布式文件系统(HDFS)中的智能用电数据集进行初始化操作,产生〈Key,Value〉键值对,其中Key定义为用户编号UserID,Value定义为用户用电信息UserInfo,即〈UserID,UserInfo〉。
步骤2 Map任务节点分别计算每一个数据块中各个样本密度,并根据最大权值积法得到若干个簇集,计算出每一个簇集元素的均值作为该簇的键值Key,Reduce节点根据键值将具有相同Key值的簇集进行数据合并。
步骤3 计算出每一个簇集数据的均值作为该簇的聚类中心,并将Value更新为该簇的中心向量,同时将Key值依次进行编号,即为该簇的簇号。
步骤4 通过Map函数计算Value中特征向量与K个初始聚类中心的欧氏距离,根据距离最小原则,找出其距离最小对应簇的簇号,从而得到更新的键值对〈Key1,Value1〉,其中Key1为距离最近簇的簇号,Value1为用电信息UserInfo。
步骤5 为了减少计算过程中的I/O通信代价,Map阶段之后,需要对每个分区具有相同Key值的信息进行合并merge。在此过程中,MapReduce模型对其合并后将得到新的键值对〈Key2,List1〈Info〉〉,其中Info={UserInfo1,UserInfo2,…,UserInfom},m为归入同一簇集内的用户数,Key2为该簇的簇号。
步骤6 定义分区函数Partition,将〈Key2,List1〈Info〉〉键值对信息按照Key2进行哈希分区,划分成r个不同的分区,并将每个分区送到相应的Reduce函数。Reduce函数将每个分区中具有相同Key值的信息进行最后的合并,得到键值结果〈Key3,List〈List1,List2,…,Lists〉〉,同时计算List中各个信息的累加均值作为更新为对应簇的中心。
步骤7 重复步骤4到步骤6,直到最终聚类结果的误差平方和达到稳定状态,并输出最终K个簇的相应信息。
改进的K-means并行数据挖掘算法流程如图3所示。
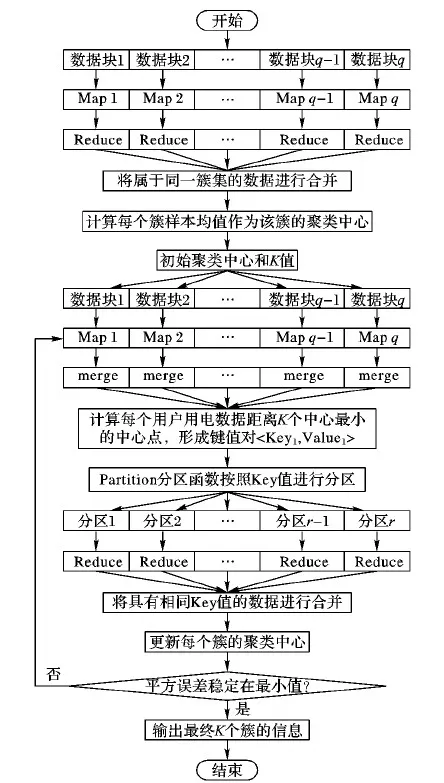
图3 改进的K-means并行数据挖掘算法流程
3 实验设计与结果分析
3.1 实验环境与数据来源
实验环境:实验使用Ubuntu12.04作为系统环境,搭建了基于Hadoop 1.0.4的6个节点的集群,包括1个Master节点和5个Slave节点。
数据来源:
1)实验一的数据来源于UCI机器学习网站,选用6类常用的测试数据集:Soybean-small、Iris、Wine、Segmentation、Ionoshpere、Pima Indians Diabetes。数据集的相关参数如表1所示。
2)实验二和实验三数据来源于北京某小区2010年4月至2010年9月400户居民的用电信息。用电信息包含:用户编号、用电属性、行业分类、电价、用电量以及用电时间等。每户居民用电情况每15 min按用电时间段被记录成一条数据,并按行存储在文件中,每一行数据占10 B。原始用电数据经过数据预处理得到规范化的特征矩阵,包括用户编号、峰时耗电率、负荷率、谷电负荷系数以及平段用电量百分比,以此建立用户用电分析的数据维度模型。
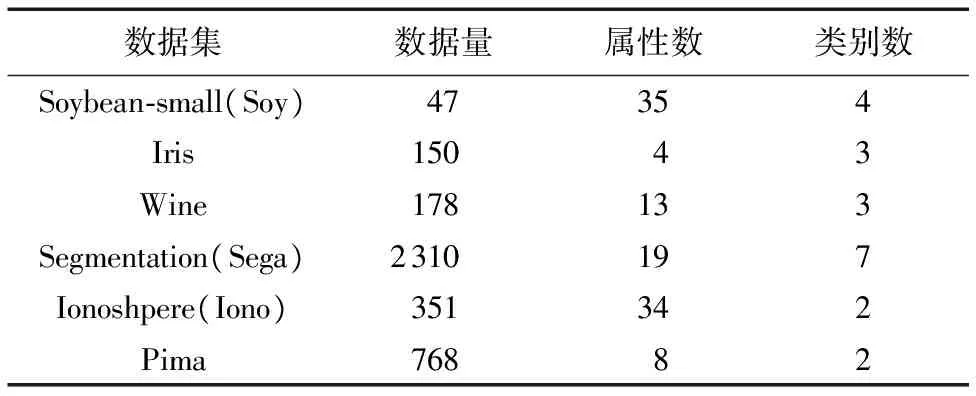
表1 UCI数据集的相关参数
3.2 实验结果分析
本文基于Hadoop平台和改进K-means算法的居民用电数据的分析,完成以下几个实验。
1)实验一。为了验证改进的K-means聚类算法的有效性,选用了UCI网站的部分数据集,分别采用传统K-means、文献[12]中的算法以及本文改进的算法进行对比实验。聚类结果通过以下参数进行衡量比较:Adjust Rand Index、聚类准确率。
图4中的聚类结果的参数比较表明:本文改进算法的Adjust Rand Index参数是最优的,准确率也最高,且聚类准确率比传统K-means算法平均高31个百分点,比文献[12]中算法高18个百分点。
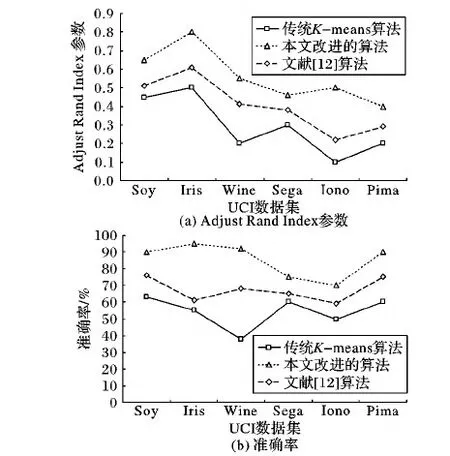
图4 不同算法对UCI数据集的聚类结果
2)实验二。选用不同大小的居民用电数据量,分别进行单机模型下的数据聚类和MapReduce并行模型下的数据聚类实验,并计算出完成聚类的时间。MapReduce并行数据聚类模型下设置1个从节点、2个从节点和4个从节点进行对比实验。
单机模型和MapReduce并行模型下的数据聚类耗时对比如图5所示。
图5中的聚类时间对比曲线表明:当处理小规模数据时(5 000 000、10 000 000),MapReduce模型下多节点和单机模型相比,聚类耗时没有明显提升。由于在此时的并行模型下,K-means算法聚类时间较短,主要耗时集中在并行节点的任务启动和任务分配上,因而并没有体现出并行处理的高效性;当数据量达到一定规模时(数据量大于100 000 000),MapReduce模型下多节点处理数据是的聚类耗时要明显优于单机模型,并且MapReduce模型下节点数越多,其聚类效率越高,说明提出的并行挖掘算法能够高效处理海量用电数据。

图5 单机模型和MapReduce并行模型下的数据聚类耗时对比
3)实验三。基于Hadoop平台和改进的K-means算法,根据用电信息完成用户的聚类任务。根据数据预处理后得到的用户用电信息特征向量,将用电信息相似的用户进行聚类,同时绘出此类用户的用电负荷曲线。
每一类用户的用电负荷曲线如图6所示。
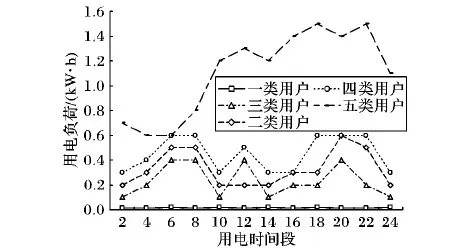
图6 各类用户用电负荷曲线
由图6可知:用户类型最终分为五类,每一类用户类型具有不同的行为特征。针对一类用户:全时段用电量很低,其耗电来源于线损,主要为闲置房居民用户。二类用户:全天有两个高峰用电时段,分别在7:00以及20:00,主要为上班族用户。三类用户:全天有三个高峰时段,分别在7:00、12:00以及20:00,主要为退休老人族用户。四类用户:与三类用户相似,具有三个高峰时段,但峰时用电量要高于三类,主要为二类与三类的混合用户,即上班族+退休老人族用户。五类用户:全时段处于高用电量状态,主要为商业用户。
根据图5中分析出的用户类型,未来电网公司可以针对不同类型的用户制定相应的用电策略,指导居民科学合理用电。同时,用户的用电行为分析对于电网公司制定合理的阶梯电价也具有一定的指导意义。
4 结语
本文以海量用电数据为基础,研究了居民用电数据分析模型架构,并提出了一种基于云计算和改进K-means算法的用电数据分析方法。具体包括以下几个方面的工作:
1)传统K-means聚类算法中存在初始聚类中心和最优K值难确定的问题。本文提出了一种加入密度参数的改进方法,在选取初始聚类中心时考虑数据集中样本密度,定义了样本密度、簇内样本平均距离的倒数以及簇间距离三者的乘积为权值积,通过最大权值积来依次确定初始中心和K值,提高了聚类的准确率。
2)提出了一种基于云计算和改进K-means算法的用电数据分析方法。首先通过对用户用电数据的预处理,提取用电数据中各个用户的峰时耗电率、负荷率、谷电负荷系数以及平段用电量百分比等特征,建立数据向量维度;然后用改进的K-means算法对数据进行聚类分析,并以MapReduce模型实现算法的并行化;最后根据聚类结果对用户的用电行为进行分析,提取每一类用户的特征。实验结果表明,提出的分析方法稳定、高效、可靠。
通过提出的一种基于云计算和改进K-means算法的海量用电数据分析方法,挖掘出用电数据中有价值信息,分析用户用电行为,对电力调度以及电价机制的制定具有重要的指导性意义。下一步,结合分析模型的用户聚类结果,针对每一类用户进行电力短期负荷预测方面的研究。
References)
[1] 张东霞,苗新,刘丽平,等.智能电网大数据技术发展研究[J].中国电机工程学报,2015,35(1):2-12.(ZHANG D X, MIAO X, LIU L P, et al. Research on development strategy for smart grid big data [J]. Proceedings of the CSEE, 2015, 35(1): 2-12.)
[2] 彭小圣,邓迪元,程时杰,等.面向智能电网应用的电力大数据关键技术[J].中国电机工程学报,2015,35(3):503-511.(PENG X S, DENG D Y, CHENG S J, et al. Key technologies of electric power big data and its application prospects in smart grid [J]. Proceedings of the CSEE, 2015, 35(3): 503-511.)
[3] 沈玉玲,吕燕,陈瑞峰,等.基于大数据技术的电力用户行为分析及应用现状[J].电气自动化,2016,38(3):50-52.(SHEN Y J, LYU Y, CHEN R F, et al. Power user behavior analysis and application status based on big data technology [J]. Power System & Automation, 2016, 38(3): 50-52.)
[4] 王德文,孙志伟.电力用户侧大数据分析与并行负荷预测[J].中国电机工程学报,2015,35(3):527-537.(WAND D W, SUN Z W. Big data analysis and parallel load forecasting of electric power user side [J]. Proceedings of the CSEE, 2015, 35(3): 527-537.)
[5] 孙志伟.大数据环境下用电行为分析的研究[D].北京:华北电力大学,2015.(SUN Z W. Study on behavior analysis of electricity in big data environment [D]. Beijing: North China Electric Power University, 2015.)
[6] 孙吉贵,刘杰,赵连宇.聚类算法研究[J].软件学报,2008,19(1):48-61.(SUN J G, LIU J, ZHAO L Y. Clustering algorithms research [J]. Journal of Software, 2008, 19(1): 48-61.)
[7] 王惠中,刘轲,周佳,等.电力系统短期负荷预测建模仿真研究[J].计算机仿真,2016,33(2):175-179.(WANG H Z, LIU K, ZHOU J, et al. Pretreatment of short-term load forecasting based onK-means clustering algorithm [J]. Computer Simulation, 2016, 33(2): 175-179.)
[8] 赵文清,龚亚强.基于KernelK-means的负荷曲线聚类[J].电力自动化设备,2016,36(6):203-207.(ZHAO W Q, GONG Y Q. Load curve clustering based on KernelK-means [J]. Electric Power Automation Equipment, 2016, 36(6): 203-207.)
[9] 李亚,刘丽平,李柏青,等.基于改进K-means聚类和BP神经网络的台区线损率计算方法[J].中国电机工程学报,2016,36(17):4543-4551.(LI Y, LIU L P, LI B Q, et al. Calculation of line loss rate in transformer district based on improvedK-means clustering algorithm and BP neural network [J]. Proceedings of the CSEE, 2016, 36(17): 4543-4551.)
[10] 许元斌,李国辉,郭昆,等.基于改进的并行K-means算法的电力负荷聚类研究[J]. 计算机工程与应用,2017,53(17):260-265.(XU Y B, LI G H, GUO K, et al. Research on parallel clustering of power load based on improvedK-means algorithm [J]. Computer Engineering and Applications, 2017, 53(17): 260-265.)
[11] 张素香,刘建明,赵丙镇,等.基于云计算的居民用电行为分析模型研究[J].电网技术,2013,37(6):1542-1546.(ZHANG S X, LIU J M, ZHAO B Z, et al. Cloud computing-based analysis on residential electricity consumption behavior [J]. Power System Technology, 2013, 37(6): 1542-1546.)
[12] 程艳柳.基于云计算的智能电网数据挖掘的研究[D].北京:华北电力大学,2013.(CHENG Y L. Research on smart grid data mining based on cloud computing [D]. Beijing: North China Electric Power University, 2013.)
[13] SHVACHKO K, KUANG H, RADIA S, et al. The Hadoop distributed file system [C]// Proceedings of the 2010 IEEE Symposium on MASS Storage Systems and Technologies. Washington, DC: IEEE Computer Society, 2010: 1-10.
[14] DEAN J, GHEMAWAT S. MapReduce: simplified data processing on large clusters [C]// Proceedings of the 2004 Conference on Symposium on Operating Systems Design & Implementation. Berkeley, CA: USENIX Association, 2004: 10-10.
[15] 黄韬,刘胜辉,谭艳娜.基于K-means聚类算法的研究[J].计算机技术与发展,2011,21(7):54-57.(HUANG T, LIU S H, TAN Y N. Research of clustering algorithm based onK-means [J]. Computer Technology and Development, 2011, 21(7): 54-57.)
This work is partially supported by the Technology Foundation of China Electric Power Research Institute (XXB51201603155), the Technology Foundation of State Grid Economic and Technological Research Institute (15JS191).
ZHANGChengchang, born in 1975, Ph. D., associate professor. His research interests include energy Internet, power big data, data mining, cyber-physical systems.
ZHANGHuayu, born in 1990, M. S. candidate. His research interests include data mining.
LUOJianchang, born in 1990, M. S. candidate. His research interests include cyber-physical systems, big data.
HEFeng, born in 1962, professor. His research interests include big data, communication technology.
