动态混沌蚁群系统及其在机器人路径规划中的应用

李 娟，游晓明，刘 升，陈 佳

(1.上海工程技术大学 电子电气工程学院，上海 201600； 2.上海工程技术大学 管理学院，上海 201600)(*通信作者电子邮箱yxm6301@163.com)

0 引言

移动机器人路径规划问题是机器人的研究热点之一。目前机器人路径规划主要解决3个问题：1)使机器人从起始点到达目标点；2)能绕过障碍物；3)在解决以上问题的前提下，机器人的运动轨迹要尽量优化[1]。从路径规划的环境感知角度的划分有：基于环境模型的规划方法、基于事例学习的规划方法和基于行为的规划方法；从目标范围划分有：全局路径规划和局部路径规划；从随着时间的变化规划环境是否变化的划分有：静态和动态路径规划。路径规划问题通常采用的算法包括：栅格法、可视图法、遗传算法(Genetic Algorithm, GA)等[2]。

群智能优化算法是人们通过观察自然环境中的群体，将其复杂的行为分解成一个个数学模型，其易于实现、鲁棒性强等特点，使得群智能优化算法成为一种热门的进化算法。这种算法包括蚁群优化(Ant Colony Optimization, ACO)算法、遗传算法、粒子群优化(Particle Swarm Optimization, PSO)算法等，其中蚁群算法是1991年由Dorigo等[3]提出的一种新型模拟进化算法，蚁群算法是受到真实蚂蚁行为特别是其觅食行为的启发，利用正反馈、自组织和分布式协作来寻找最优路径，它有强鲁棒性、并行分布式计算、全局搜索能力强、易与其他问题结合等优点，使得其成功运用到机器人路径规划、旅行商问题(Traveling Salesman Problem， TSP)、图像识别等领域[4]。

蚁群算法的主要特点是正反馈和分布式计算，但是对于大规模机器人路径规划的问题，解的质量不高。针对蚁群算法收敛速度慢的不足，文献[5]提出了最优最差蚂蚁系统(Best-Worst Ant System, BWAS)，BWAS的基本思想是增强迭代过程中较优路径的信息素并减弱较差路径的信息素，使得蚂蚁向较优路径靠近，以提高算法的收敛速度；但文献[6]指出这种做法可能会使算法陷入局部最优从而无法找到全局最优解。Ghumman等[7]提出了最大最小蚂蚁系统(Max Min Ant System, MMAS)，该算法通过限定信息素值的范围来避免某条路径上的信息素浓度过大或者过小，并以此来增加种群多样性，扩大解的范围，避免了算法早熟、陷入局部最优解的现象；但是，MMAS的收敛速度比较慢，搜索时间也比较长。Boussaid等[8]提出了蚁群系统(Ant Colony System, ACS)，ACS的种群多样性好，不过其搜索效率较低，收敛速度比较慢。

近年来，非线性动力学的研究发展迅速，科学家将其应用到群智能算法中，特别是混沌在优化算法方面取得的进展，引起了学者们的关注。Gandomi等[9]提出了将混沌算子引入蝙蝠算法(Bat Algorithm, BA)中，混沌蝙蝠算法可以提高全局最优的可靠性和结果的质量。Javidi等[10]提出混沌遗传算法(Chaos Genetic Algorithm, CGA)，使用Tent混沌映射和Logistic混沌映射来生成混沌值，可以避免算法局部收敛，实验结果表明CGA减少了优化过程中的迭代次数，并显著提高了GA的性能。Wang[11]在2009年提出了将混沌蚁群算法应用到基于QoS(Quality of Service)的网络服务组合中，用混沌变量来克服蚁群算法效率低、易陷入局部最优的不足，且蚁群算法的正反馈性也降低了混沌搜索的盲目性，两者相互改进，实验表明混沌蚁群算法是高效的。

为了提高ACS算法的收敛速度、增加种群多样性，本文对ACS算法引入动态混沌算子，以增加种群多样性、避免陷入局部最优、提高解的质量，在迭代后期则将混沌算子去除以提高其收敛速度，来平衡ACS算法的收敛速度和种群多样性的关系。本文将其应用到基于环境模型的静态全局路径规划中，实验结果表明所提算法是可行且有效的。

1 相关工作

1.1 蚁群系统

受自然界中蚂蚁群体的觅食行为的启发，Dorigo等[3]提出了ACO。蚂蚁个体之间是通过信息素(pheromone)来传递信息的，蚂蚁通过路径后会在路径上留下信息素，同时可以感知其他蚂蚁留下的信息素。在觅食过程中，某条路径通过的蚂蚁越多，信息素浓度越高，其他蚂蚁就越倾向于选择该条路径，这种行为就是一种信息正反馈现象。在相同的时间之内，路径越短，则走过的蚂蚁数目越多，信息素浓度也就越强。蚂蚁之间就是通过这种信息交流的方式来找到巢穴与食物源之间的最短路径，并由此提出了蚁群算法。

针对基本蚁群算法的缺陷，科学家提出了各种改进算法，Dorigo等[3]提出了精英蚁群系统(Elitist Ant colony System, EAS)，EAS的提出是基于遗传算法的，其将迭代过程中拥有较优路径的蚂蚁保留到下一代，以提高算法的收敛速度；但是，当精英蚂蚁的数量选择不当时，算法将很快聚集在局部路径导致算法早熟，陷入局部最优解[12-13]。Bullnheimer等[14]提出了基于排序的蚂蚁系统(rank-based Ant System, ASrank),ASrank中每只蚂蚁根据其所经路径长度进行排序，其释放的信息素值根据它们各自的等级高低来决定。ACS是一种经典的改进算法[8]。在状态转移过程中，蚂蚁利用伪随机概率选择下一个节点:

(1)

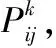
(2)

其中s是蚂蚁k在当前迭代中未游历的所有候选解。

蚂蚁从节点i到j之后，进行局部信息素更新，如式(3)所示：

τij=(1-λ)τij+λτ0

(3)

其中：λ为局部信息素残留因子；τ0表示路径信息素初始值，文献[3]中说明了该值的3种可能取值，实验结果表明，τ0直接为给定值时实验结果最好，故本文将τ0设为定值。信息素更新是为了给更短的路径分配更多的信息素，反映了ACS的正反馈性。

在一次迭代之后，仅对当前循环最短的路径应用全局信息素更新规则即式(4)，这在一定程度上可以提高算法的收敛速度。

τij=(1-ρ)τij+ρΔτij

(4)

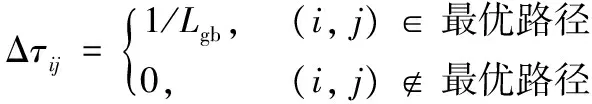
(5)

其中：ρ为全局信息素残留因子；Lgb表示在一次循环中最优蚂蚁k走过的总长度即当代最短路径。信息素更新公式(3)～(4)包含了蚂蚁走过路径后信息素的增量和信息素挥发，是为了模拟信息素强度的变化。

1.2 移动机器人的路径规划

路径规划一般分为三个环节：环境建模、路径搜索和路径平滑(本文不考虑路径平滑这一环节，在搜索范围内，默认路径可行)。环境建模的方法有：可视图法、自由空间法、Maklink图法、栅格法、Voronoi图法等。由于栅格法具有精度高、易于实现等优点，本文将采用最经典的栅格法。

栅格法的原理是：假设机器人的工作空间是在二维平面上的有限区域，而且工作空间中分布的障碍物是静态的、有限个且位置及大小都是已知的。将工作区域划分为单位大小的栅格，若栅格内无障碍物则称为自由栅格，用白色表示，记为0；否则称为障碍栅格，用黑色表示，记为1。当机器人四周无障碍且不处于边缘栅格时，有8个方向可以移动到相邻栅格，分别是右、右上、右下、左、左上、左下、正上、正下。可以根据机器人的起始点、目标点和障碍物，建立一个栅格坐标系。

1.3 混沌优化算法

混沌不同于随机、混乱，它对初始条件非常敏感。混沌理论通常被说明为由Lorenz[15]描述的所谓的“蝴蝶效应”，是一种发生在确定性非线性系统中的有界动态行为。混沌序列有三个主要的属性：遍历性、随机性、初值敏感性，混沌优化就是利用混沌序列进行的优化搜索。混沌的遍历性质可以确保混沌变量在一定范围内不重复地遍历所有状态，这可以作为一种优化机制，避免算法落入局部最优解[16]，因此，这样的群体不仅能得到最短路径，而且能保证种群多样性。目前，有10余种常用的混沌映射，本文在表1中给出了5种经典的混沌映射表达式，并在图1中给出了不同混沌映射的混沌图形[11，17]。

表1 混沌映射表达式

图1 混沌映射的曲线

由图1可知，这几种混沌映射的混沌性都很好，但是Logistic混沌映射简单易实行，则本文选用典型的Logistic混沌映射,迭代公式如下：

zi+1=μzi(1-zi);

i=0,1,2,…,z0∈[0,1],μ∈(2,4]

(6)

通过式(6)，可以得到一系列相应的值z1,z2,…。

当Logistic混沌映射参数μ值满足参数范围时，改变初始值，可以得到混沌状态，故本文选用经典的μ=4。

通过讨论μ与z0的值，可以得出结论：1)μ=4时，改变初值z0的值(z0≠0,0.25,0.5,0.75,1)，系统一直为混沌状态，如图2；2)z0=0,0.25,0.75,1，μ=4时，系统的动态形态都是只有一个周期点，如图3。

实验结果表明，当μ=4，z0≠0,0.25,0.5,0.75,1时，系统为完全混沌状态：

当μ=4，z0=0,1时，zi=0恒成立；

当μ=4，z0=0.25时，zi=0.75(i≥1)恒成立；

当μ=4，z0=0.5时，z1=1,zi=0(i=2,3,…)恒成立；

当μ=4，z0=0.75时，zi=0.75(i≥0)恒成立；

因此本文的参数将设置为μ=4，z0=0.1。下面是使用Matlab仿真Logistic映射，绘制改变μ的值时对应z的值，让初始系统的值z0=0.1，迭代次数为200次。μ是控制参数，当μ=4，Logistic映射处于完全混沌状态。

图2 不同初始值时的Logistic混沌图

图3 异常初始值参数的Logistic混沌图

2 改进的混沌蚁群系统

针对ACS的不足，本文提出了在蚁群系统中引入动态混沌算子，用动态混沌算子来改变信息素的更新方式，以提高算法收敛速度、避免落入局部最优、增加种群多样性。

2.1 动态混沌算子

基于ACS的种群多样性差、收敛速度慢、易陷入局部最优解的不足，本文的改进措施是引入动态混沌算子，在迭代前期加入混沌算子，以调整路径中的信息素值，来增加算法的种群多样性，在迭代后期去除混沌扰动来提高算法的收敛速度。全局信息素更新式(4)修改为式(7)：

τij(t+1)=(1-ρ)τij(t)+ρΔτij(t)+R

(7)

(8)

其中：zij为混沌变量，是由Logistics混沌映射式(6)迭代得到的；p为系数以调整混沌算子的值使其适应ACS算法全局信息素的值；NC为算法的当前迭代次数，NC0为迭代阈值，本文通过实验证明当NC0为20时，动态混沌蚁群系统所得结果将更优、更稳定，如表2。

当ACS初始化时，每条路径上的信息素都是相同的，使得蚂蚁难以从选择概率相同的路径中快速找到更好的路径，从而导致算法易陷入局部最优且收敛速度较慢，动态混沌蚁群系统加入混沌算子可以很好地解决这一问题。动态混沌蚁群系统在迭代初期利用混沌算子增加全局路径信息素值，以增加种群多样性，使算法避免陷入最优解，并得到较好的最优解；在迭代后期将去除混沌算子，使算法的全局信息素增长减缓，以提高算法的收敛速度。

利用混沌算子的遍历性可以增加原始ACS的种群多样性，利用ACS的正反馈性也可以降低混沌变量的随机性、盲目性，两者相互改进，故使用混沌序列是必要的。通过本文的实验结果，表明引入动态混沌算子后，动态混沌蚁群系统所得全局最优解更优，与传统蚁群系统相比能够更好地平衡收敛速度和种群多样性之间的关系。

2.2 改进的混沌蚁群系统

本文改进算法的流程如图4所示。

图4 动态混沌蚁群系统流程

本文提出的改进算法的伪代码如下：

Begin

初始化参数(蚂蚁数目M、禁忌表Tabu、路径信息素值τ0、最大迭代次数NCmax、当前最优解Lbest等)

While 迭代次数NC<最大迭代次数NCmax

do 将M只蚂蚁随机放到起始点i上，并将该起始点i放入禁忌表Tabu中

While 有蚂蚁未完成一次循环

do 根据伪随机概率公式(式(1))选择下一个节点j，再将节点j放入禁忌表Tabu中

对路径进行局部信息素τij更新(式(3))

end

记录第k只蚂蚁的路径长度Lk

if 当前最优解Lbest>Lk

thenLbest←Lk

引入动态混沌算子对当前最短路径进行全局信息素τ更新(式(7))

NC←NC+1

end

Output:当前蚁群中的最短路径，即为最优路径

End

3 仿真实验结果及分析

为了验证动态混沌蚁群系统的可行性与有效性，本文在Matlab环境下将对以下5种地图进行仿真，并与传统蚁群系统(ACS)、基于精英策略的蚂蚁算法(EAS)、基于排序的蚂蚁算法(ASrank)进行比较。

本文引入动态混沌算子以平衡算法的种群多样性与收敛速度之间的关系，在迭代前期引入混沌算子来增加算法的种群多样性，在迭代后期去除混沌算子来提升算法的收敛速度。本文通过实验表明，动态混沌算子的迭代阈值NC0为20时，算法结果更优，如表2所示。

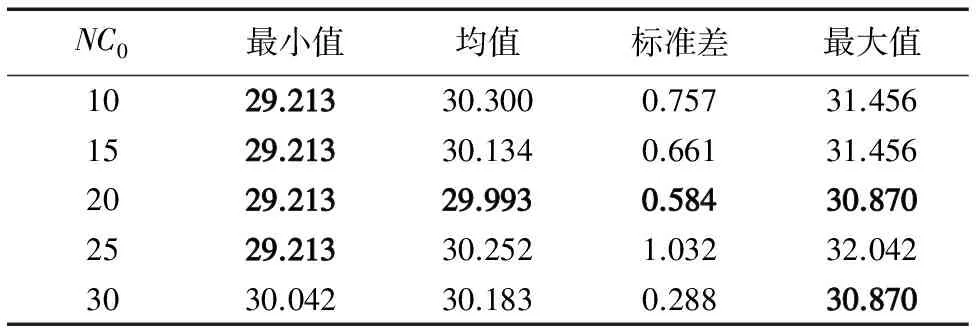
表2 动态混沌蚁群系统中不同参数NC0所得的解

表2为动态混沌蚁群系统在同一路径规划环境下运行10次，改变动态混沌算子的参数NC0的值，其他参数不变的实验数据。由表2可知，当动态混沌算子的参数NC0为10，15，20，25时，运行10次动态混沌蚁群系统所得解的最小值都为29.213 2，即参数NC0为10，15，20，25时，动态混沌蚁群系统都有可能得到最优解，但是当NC0为20次时，动态混沌蚁群系统的均值、标准差都为最小，故此时动态混沌蚁群系统所得解的质量更稳定。由此，动态混沌蚁群系统的动态混沌算子的参数NC0设为20次。

本文实验中所用参数设置如表3所示。

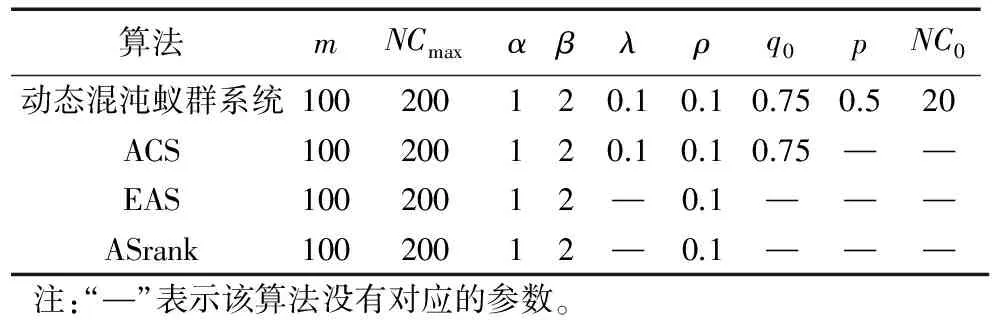
表3 各算法实验参数设置

对于20×20的障碍图(如图5所示)，由全局最优路径比较可以看出，动态混沌蚁群系统的路径结果(实线)优于ACS算法的路径结果(虚线)，迭代情况比较图中动态混沌蚁群系统的最短路径明显优于ACS、EAS、ASrank。对于复杂情形下50×50的障碍图(如图6)，动态混沌蚁群系统的结果同样优于ACS、EAS、ASrank，且收敛代数也较少。

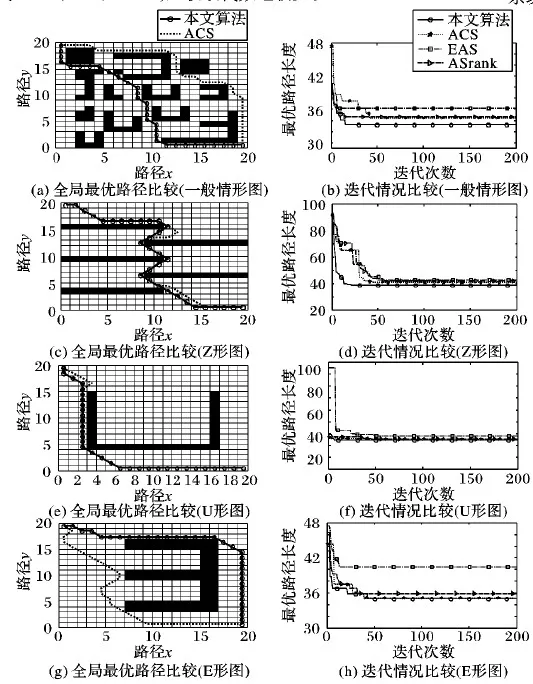
图5 20×20环境中不同情形下的迭代情况对比

Tab. 4 Performance comparison of four algorithms under different environments

图5(a)为动态混沌蚁群系统与ACS算法全局最优路径的对比，由该图可以看出，对于简单环境下的路径规划问题，动态混沌蚁群系统与ACS算法都可以找到最优路径，但是由图5(b)的迭代情况对比可以看出,动态混沌蚁群系统的最优路径(33.313 7)比ACS算法(34.485 3)更短，且得到最优路径所需迭代次数也更少(如表4)。动态混沌蚁群系统与EAS、ASrank相比，虽然动态混沌蚁群系统的寻优迭代次数比EAS多一些，但是最优路径是更好的，详细数据如表4。动态混沌蚁群系统引入动态混沌算子，来平衡种群多样性与收敛速度的关系，在迭代前期引入混沌算子，使得算法的种群多样性增加，所以与ACS、EAS、ASrank相比可以得到较优的最优路径，在迭代后期则去除混沌算子，来提高收敛速度，因此动态混沌蚁群系统在得到较优的最短路径的同时，收敛速度也较快。

从图5(c)可以看出，对于特殊环境下的较小规模路径规划问题，动态混沌蚁群系统与ACS算法相比，动态混沌蚁群系统的最优路径更优。由于动态混沌蚁群系统能够平衡种群多样性与收敛速度的关系，动态混沌蚁群系统与ACS、EAS、ASrank相比(如图5(d))，最优路径质量相差不多，其中动态混沌蚁群系统路径是最短的，值为38.870，ACS、EAS和ASrank分别为40.870，42.870和42.041 6，但是动态混沌蚁群系统收敛速度更快。

图5(e)～(f)中的路径规划问题是较小规模下的一种特殊环境，从图5(e)可以看出，动态混沌蚁群系统能够较优地避开陷阱，从而得到较好的最优解；从图5(f)的迭代情况比较可以看到，动态混沌蚁群系统较其他3种算法的结果也更好，动态混沌蚁群系统的路径为34.485 3，比ACS、EAS和ASrank的路径都短，且收敛速度最快(如表4)，故动态混沌蚁群系统能够在找到最优解的同时，提高收敛速度。

图5(g)～(h)中的特殊环境下的路径规划问题易导致结果陷入局部最优，如图5(g)中的ACS算法，但是由于动态混沌蚁群系统前期的种群多样性较好，因此动态混沌蚁群系统能够很好的找到最优解；图5(h)中可以看出，动态混沌蚁群系统的最优解较好，收敛速度也较优，能够较好地平衡种群多样性与收敛速度的关系。

图6是较大规模的路径规划问题，由于动态混沌蚁群系统在迭代前期引入混沌算子，使得种群多样性增加，解的质量也更好，而且动态混沌蚁群系统在迭代后期去除混沌算子，以提高收敛速度，因此，对于大规模的路径规划问题，动态混沌蚁群系统解的质量与收敛速度都优于ACS、EAS和ASrank，动态混沌蚁群系统同样能够较好地平衡种群多样性与收敛速度的关系。

表4为本文算法(动态混沌蚁群系统)、ACS、EAS和ASrank四种算法的最优路径长度和达到最优路径时迭代次数的具体实验数据，由表4可以看出动态混沌蚁群系统解的质量更高，且收敛速度也较快。表4中：Lb为最优路径长度；NCb为达到最优路径时的迭代次数，T为达到收敛时所用时间(单位：s)。

由表4可以看出，对于图5(c)～(h)，动态混沌蚁群系统达到收敛时的路径长度、迭代次数和运行时间与ACS、EAS和ASrank相比，都是最优的。对于图5(a)、(b)，本文改进算法比ACS和ASrank的收敛速度、最优路径长度都优秀，因此本文算法与ACS和ASrank相比，解的质量最优；图5(a)、(b)中本文改进算法与EAS的收敛时间分别为4.92 s和4.34 s，但是本文改进算法与EAS的最优路径长度分别为33.313和36.142，本文改进算法最优路径长度比EAS大幅度减少，因此本文改进算法能够很好地平衡最优路径长度与收敛速度的关系，解的质量更优。图5(g)、(h)的情况与图5(a)、(b)相似，因此，动态混沌蚁群系统对ACS引入动态混沌算子，可以平衡算法的收敛速度和最优路径长度之间的关系，提高解的质量。

图6 50×50环境迭代情况对比

4 结语

传统蚁群系统存在种群多样性不佳、解的质量不高等不足，仅仅依赖传统的信息素更新方式将难以找到最优解，且容易陷入局部最优，因此本文提出了在迭代前期对ACS的全局信息素更新方式引入Logistic混沌算子，避免了算法陷入局部最优解，且收敛速度也较快，在迭代后期则去除Logistic混沌算子，以提高收敛速度，避免因为种群多样性的增加而引起收敛速度的降低。仿真结果表明，动态混沌蚁群系统与传统算法相比，对于简单环境下的路径规划问题(20×20环境)，动态混沌蚁群系统解的质量更高、种群多样性更好，并且对于复杂环境下的路径规划问题(50×50环境)，动态混沌蚁群系统可以避免陷入局部最优且解的质量更好。动态混沌蚁群系统虽然能够很好地找到最优解，但是其收敛速度还不能保证每种类型的路径规划问题都能达到最优。下一步将进一步研究混沌算子模型，用于改进蚁群算法，从而进一步提高解的质量。

References)

[1] 朱大奇,颜明重.移动机器人路径规划技术综述[J].控制与决策,2010,25(7):961-967.(ZHU D Q, YAN M Z. Summary of mobile robot path planning technology [J]. Control and Decision, 2010, 25(7): 961-967.)

[2] 许亚.基于改进的人工势能场的移动机器人路径规划研究[J].科技展望,2016,26(33):77-78.(XU Y. Research on mobile robot path planning based on improved artificial potential field [J]. Science and Technology, 2016, 26(33): 77-78.)

[3] DORIGO M, MANIEZZO V, COLORNI A. The ant system: optimization by a colony of cooperating Agents [J]. IEEE Transactions on Systems, Man, and Cybernetics—Part B, 1996, 26(1): 1-13.

[4] 夏小云,周育人.蚁群优化算法的理论研究进展[J].智能系统学报,2016,11(1):27-36.(XIA X Y, ZHOU Y R. Theoretical research progress of ant colony optimization algorithm [J]. Journal of Intelligent Systems, 2016, 11(1): 27-36.)

[5] 李士勇.蚁群算法及其应用[M].哈尔滨:哈尔滨工业大学出版社,2004:112-126.(LI S Y. Ant Colony Algorithm and Its Application [M]. Harbin: Harbin Institute of Technology Press, 2004: 112-126.)

[6] THEPPHAKORN T, PONGCHAROEN P, HICKS C. An ant colony based timetabling tool [J]. International Journal of Production Economics, 2014, 149(3): 131-144.

[7] GHUMMAN N S, KAUR R. Dynamic combination of improved max-min and ant colony algorithm for load balancing in cloud system [C]// Proceedings of the 6th International Conference on Computing, Communication and Networking Technologies. Piscataway, NJ: IEEE, 2015: 1-5.

[8] BOUSSAID I, LEPAGNOT J, SIARRY P. A survey on optimization metaheuristics [J]. Information Science,2013, 237(19): 82-117.

[9] GANDOMI A H, YANG X-S. Chaotic bat algorithm [J]. Journal of Computational Science, 2014, 5(2): 224-232.

[10] JAVIDI M, HOSSEINPOURFARD R. Chaos genetic algorithm instead genetic algorithm [J]. The International Arab Journal of Information Technology, 2015, 12(2): 163-168.

[11] WANG Y. Application of chaos ant colony algorithm in Web service composition based on QoS [J]. International Forum on Information Technology and Applications, 2009, 172(2):25-227.

[12] TAO W Q, YANG G, ZHANG J Y. Fault section locating for distribution network with DG based on improved ant colony algorithm [C]// Proceedings of the 2016 Power Electronics and Motion Control Conference. Piscataway, NJ: IEEE, 2016: 1985-1989.

[13] PRAKASAM A, SAVARIMUTHU N. Metaheuristic algorithms and probabilistic behaviour: a comprehensive analysis of ant colony optimization and its variants [J]. Artificial Intelligence Review, 2016, 45(1): 97-130.

[14] BULLNHEIMER B, HARTL R F, STRAUB C. A new rank based version of ant system — a computational study [J]. Central European Journal of Operations Research, 1999, 7(1): 25-38.

[15] LORENZ N. Deterministic non periodic flow [J]. AMS Journal, 1963, 20(2): 130-141.

[16] WANG Y, YAO M.A new hybrid genetic algorithm based on chaos and PSO [C]// Proceedings of the 2009 IEEE International Conference on Intelligent Computing and Intelligent Systems. Piscataway, NJ: IEEE, 2009: 699-703.

[17] SHAHRZAD S, SEYEDALI M, ANDREW L. Biogeography-based optimisation with chaos [J]. Neural Computing and Applications, 2014, 25(5): 1077-1097.

This work is partially supported by the National Natural Science Foundation of China (61673258, 61075115, 61403249, 61603242).

LIJuan, born in 1991, M. S. candidate. Her research interests include embedded control system, intelligent algorithm, robot system.

YOUXiaoming, born in 1963, Ph. D., professor. Her research interests include intelligent information processing, pattern recognition, artificial intelligence, distributed parallel intelligent processing.

LIUSheng, born in 1966, Ph. D., professor. His research interests include intelligent information processing.

CHENJia, born in 1993, M. S. candidate. Her research interests include embedded control system, intelligent algorithm, robot system.