基于动态选择启发值的改进TD-FTT算法
2018-03-20李佳佳刘晓静刘向宇夏秀峰
李佳佳,刘晓静,刘向宇,夏秀峰,朱 睿
(沈阳航空航天大学 计算机学院,沈阳 110136)(*通信作者电子邮箱lijiajia@sau.edu.cn)
0 引言
目前,关于静态路网K近邻查询研究已经相当成熟[1-3],代表性算法有基于Voronoi图的VN3(Voronoi-based Network Nearest Neighbor)算法[4];利用欧氏距离与路网距离结合的IER(Incremental Euclidean Restriction)、INE(Incremental Network Expansion)[5]算法;通过范围扩展的“岛”算法[6]等,但静态路网以行驶距离作为边的权值,在时间依赖路网中,边的权值为行驶时间。如图1所示,汽车1寻找最快到达的加油站,在图1(a)发起查询时刻为早上8:00,加油站1为返回结果,如果在早上6:00发起查询如图1(b)所示,加油站2则是离汽车1最近的加油站。由于发起查询时刻不同,返回的结果集不同,因此静态路网中求解K近邻查询的算法并不适用于时间依赖路网中,需要探索新的方法。
关于时间依赖路网K近邻查询存在一定研究[7-9]但相关研究还很不完善。Demiryurek等[10]提出TE(Time-Expanded)和TD-NE(Time-DependentKnearest neighbor with Network Expansion)算法,Cruz等[11]通过启发函数和剪枝技术提出TD-NE-A*(Time Dependent Network Expansion with A*search)算法。TE算法将边的权值离散化,无法保证权值在所有时刻取得实际值,因此造成误差并不断积累,最终可能导致结果集的错误;TD-NE算法查询中盲目扩展所有节点的邻接点,计算代价大;TD-NE-A*算法剪枝策略的设定,会漏掉查找的兴趣点,或者使到达兴趣点的代价增大,并且由于时间依赖路网中权值在高峰期和低峰期相差较大,TD-NE-A*在高峰期用全天最小值作启发值与实际值相差较大,启发效果差,因此Komai等[12]提出TD-FTT(Time Dependent Fast Travel Time)算法,该算法将总体时间分为n个时段。预处理阶段,取每个时段边的最小值构成静态路网Gmin,在Gmin中计算所有节点的C近邻。查询发起时,确定查询发起时刻位于的时段,利用该时段节点到达C近邻的最小值作启发值,因此启发值更接近实际值,启发更高效,有效解决了TD-NE算法[10]盲目扩展带来的计算量大和TD-NE-A*算法[11]启发效果差的问题。
TD-FTT算法[12]在查询阶段,由于用查询时刻所在时段的Gmin中节点到达最近邻的时间作启发值,因此必须保证查询扩展过程中节点到达下一节点的时间和到达K近邻的时间与查询发起时刻在同一时段,使实际应用受限。例如,图2中将T=60以20为间隔平均划分为三个时段,v1在ts=15时发起查询求最近邻。当扩展第一个节点v2时,到达v2的时间为25,已经跨过当前时段[0,20]。在预处理阶段,求解静态路网Gmin中的C近邻时C值和时段个数不易确定,且需计算每个时段Gmin中所有节点的C近邻,计算量大,但在查询K近邻过程中,仅利用节点最近邻的预处理信息,即C>1时,C近邻的计算没有意义,预处理信息利用率低。
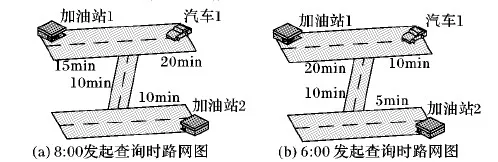
图1 时间依赖路网1近邻查询
本文针对TD-FTT算法在预处理阶段存在的计算量大、信息利用率低和查询阶段不能跨时段查询的问题,提出改进的TD-FTT(Improved TD-FTT, ITD-FTT)算法。具体改进策略如下:在预处理阶段采用网络泰森图(Network Voronoi Diagram, NVD)在静态路网Gmin中并行计算所有节点的最近邻及到达最近邻的时间,以减少计算量;在查询阶段根据查询过程节点的到达时间动态选择启发值,不受用查询时刻所在时段的最小值作启发值所带来的时段限制问题,使查询不受限。
1 时间依赖路网模型
定义1 时间依赖路网。时间依赖路网GT由集合V,E和C组成,记为GT=(V,E,C),其中V={v1,v2,…,vn}是顶点的有限集合,E={(vi,vj)|vi,vj∈V,i≠j}是连接V中两个不同顶点(顶点对)的边的有限集合,C={c(vi,vj)(t)|(vi,vj)∈E},c(vi,vj)(t):[0,T]→R+,表示在t时刻从vi到vj所耗时间,其中t∈[0,T],T为时间周期。如图2(a)为一个时间依赖路网,图2(b)~图2(f)为各边的权值函数。
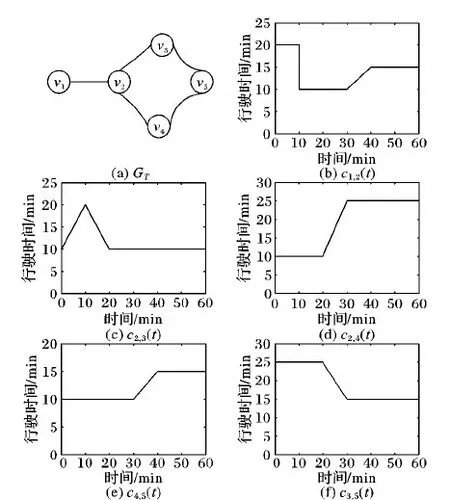
图2 时间依赖路网GT及某1 h内各边权值函数
时间依赖路网模型分为先进先出(First-In First-Out, FIFO)模型和非先进先出模型,即对于边,如果边权值函数c(vi,vj)(t)连续且处处可微,对任意t满足c(vi,vj)(t)≤t1+c(vi,vj)(t+t1);或者当边的时间函数c(vi,vj)(t)为离散值时,对任意s,t满足下列不等式s+c(vi,vj)(s)≤t+c(vi,vj)(t);具有该性质的边为FIFO边。若路网中所有边都为FIFO边,则这样的路网称为FIFO路网模型,不具有这样性质的边为非FIFO边,若路网中存在一条非FIFO边,则路网称为非FIFO路网模型。时间依赖网络中,需要满足FIFO性质;否则产生NP(Non-deterministic Polynomial)难问题[13]。目前所有关于时间依赖路网的研究都以满足FIFO性质为前提。本文所研究时间依赖路网同样满足FIFO性质。
定义2 到达时间。对于时间依赖路网GT=(V,E,C),在t时刻从vi通过边(vi,vj)到达vj的到达时间定义为AT(vi,vj,t)=t+c(vi,vj)(t) modT。

定义4 时间依赖最快路径。对于时间依赖路网GT=(V,E,C),存在u,v∈V,P(u,v)表示在t时刻出发,从u到v的所有路径的集合,如果p∈P(u,v)且对于其他所有p′∈P(u,v)满足TT(p,t)≤TT(p′,t),则p为时间依赖最快路径,定义为p=TDFP(u,v,t)。例如,在图2,在t=5时发起查询,v1到v5的时间依赖最短路径TDFT(v1,v5,5)={v1,v2,v3,v5};当t=10时,v1到v5的时间依赖最短路径TDFT(v1,v5,10)={v1,v2,v4,v5}。同一查询,查询时间不同,返回的最短路径不同。
定义5 时间依赖的K近邻查询。对于时间依赖路网GT=(V,E,C)和兴趣点集合POI⊆V,存在查询点q,查询发起时间t和目标兴趣点个数k(k>0),时间依赖路网K近邻查询返回的结果集R={vr1,vr2,…,vrk}⊆POI且对任意v属于集合POIR满足,TDFP(q,vri,t)≤TDFP(q,v,t)。
2 TD-FTT算法
TD-FTT算法是为解决时间依赖路网中利用A*查询K近邻时启发函数与实际值相差较大问题而提出的算法。
2.1 TD-FTT算法描述
TD-FTT算法分为预处理和查询两个阶段。算法将整体时间tb根据需要分割成不同时段[0,t1],(t1,t2],…,(tb-1,tb]。在预处理阶段,对每个时段(ti,ti+1]进行如下操作:1)所有边权值取当前时段权值函数最小值minc(vi,vj),构成静态路网Gmin;2)在静态路网Gmin用INE算法[5],查询所有节点的C近邻(C常值)和到达C近邻的代价TT(ti-1,ti],保存结果集,构建索引。在查询阶段,查询点q在时刻t发起查询,首先判断t所属的时段(ti+1,ti],计算q到邻接点vi的通行时间c(q,vi,t),利用预处理构建的索引查找在时间段(ti+1,ti]中vi的C近邻,取代价TT(ti-1,ti]最小的近邻,即TT(ti-1,ti]=min(TT(ti-1,ti]),令L=c(q,vi,t)+TT(ti-1,tt]作为评价函数,选取L最小的节点vi继续扩展,找到K近邻为止。
2.2 TD-FTT算法实例
以图3和表1为例,说明TD-FTT算法执行过程及TD-FTT存在的预处理阶段信息利用率低和查询阶段受时段限制的问题。在3.3节中仍使用该图和表为例,说明ITD-FTT算法执行过程及在执行过程中如何解决以上问题。
图3和表1为时间依赖路网GT及相应边的权值函数,将整体时间T=20平均分割为两个时间段[0,10],(10,20]并令C=2。由边权值函数,得到每个时段内边的最小值,构成静态路网GMIN[0,10]和GMIN(10,20],在静态路网中得到所有节点(除兴趣点外)的两个近邻poi1、poi2及到达近邻所需时间time1、time2,结果如表2所示。令查询点q=a,查询时间t=1,K=2。首先,判断查询时刻所在的时段,因为t∈[0,10],因此选择GMIN[0,10]的预处理信息;然后,遍历查询点a的邻接点{b,p2,c}并将a加入到队列VP-label,加入VP-label中的节点不再扩展;最后,分别计算各节点的AT、TT、L值,并加入到优先队列VT-label中,例如对于节点b,通过a到b的权值函数得TTb=c(a,b,1)=2.3,ATb=t+TTb=3.3。由表2可知,b的最近邻为p1且time1=1,所以评价值L=TTb+time1=3.3。p2和c各值的计算类似b,最终得到的VT-label集合如下:
VT-label={(TTb=2.3,ATb=3.3,Lb=3.3),(TTp2=3.8,ATp2=4.8,Lp2=3.8),(TTc=2.4,ATc=3.4,Lc=4.4)}。选择评价值L最小的节点继续扩展,因此在VT-label中对节点b进行出队列操作同时将b加入到队列VP-label中。与节点b相连的节点为p1,操作如上,得到VP-label={a,b},VT-label如下:{(TTc=2.4,ATc=3.4,Lc=4.4),(TTp2=3.8,ATp2=4.8,Lp2=3.8),(TTp1=6.6,ATp1=7.6,Lp1=6.6)},其中节点p2的L值最小,因此选择p2进行遍历。当选择的节点为兴趣点且TT=L,则该兴趣点为查找的目标节点,因此将p2加入到结果集NN中。重复以上操作,得到结果集NN={p1,p2},且到达目标节点的时间在时段[0,10]区间。
当查询时间t=8时,t∈[0,10],选择GMIN[0,10]的预处理信息,当扩展a的邻接点{b,c,p2}时,到达节点的时间超出时段[0,10],则到达目标节点的时间必然在该时段外。
TD-FTT算法查询点q必须在查询时刻t所属的时段t∈(ti-1,ti]内到达K近邻,当查询时间t与时段上限ti接近时,不能保证q到达K近邻的时间与查询发起时刻在同一时段。另外,在预处理阶段,计算每个时段(ti,ti+1]内所有节点在静态路网中的C近邻和到达C近邻的时间来构建索引。如上例在查询阶段,仅利用节点到达最近所需的时间min(TT(ti,ti+1]),因此当C>1时,C近邻的计算没有意义。本文针对以上问题,预处理阶段改进索引结构,在查询阶段动态选择启发值解决不能跨时段查询的问题。
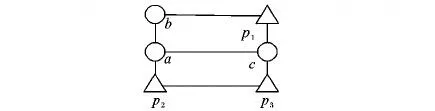
图3 时间依赖路网GT

Tab. 1 Time function of each edge

表2 两个区间的预处理信息
3 ITD-FTT算法
ITD-FTT在预处理阶段和查询阶段对TD-FTT算法进行改进。由于NVD[14]单元具有在其范围内的节点,都以该NVD单元的中心点为最近邻的性质。因此,在预处理阶段,首先计算各时段的静态路网Gmin,然后利用NVD单元上述性质,并行计算每个Gmin中所有节点vi∈V(i=1,2,…,n)的最近邻及达最近邻所需的时间TT(ti-1,ti]。查询阶段,根据节点vi到达时间AT(vi,vi+1,tk)所在的时段,动态选择相应时段的Gmin中节点到达最近邻所需的时间TT(ti-1,ti]作为启发值,解决了以查询时刻所在时段对应的Gmin中节点到达最近邻值作启发值带来的时段限制问题。
3.1 预处理阶段
介绍预处理阶段之前,对NVD及相关性质进行描述:

性质1 NVD单元范围内的所有节点,以NVD的中心点为最近邻[14]。
在预处理阶段,将整个周期T根据实际路网权值变化规律,分割为n个互不相交的时段,对每个时段进行如下操作:
1)边权值取时段内时间函数的最小值,构成静态路网称为Gmin,边权值满足E={|(vi,vj)|=minc(vi,vj)(ti-1,ti]}。
2)在时段内,将所有兴趣点作为NVD的中心点,构建NVD单元,得到每个节点在时段内的最近邻及到达最近邻的代价[11]。用Vgene(vi)表示vi的最近发起点集合,Vpred(vi)表示vi的前驱集合,dgene(vi)表示vi到当前最近发起点的最短路径,Vadja(vmin)表示vmin的邻接点集合,dS(vmin,vk)表示vmin到vk的距离,利用NVD计算节点最近邻如算法1所示。
算法1 NVD并行计算最近邻算法。
输入:静态路网Gmin,兴趣点集合POI。
输出:NVD,得到节点最近邻及到达最近邻的时间。
1)
对所有中心点及非中心点进行初始化
2)
for 对每个中心点pi∈POI及每个节点vido
3)
Vgene(pi)={pi},Vpred(pi)={p0},dgene(vi)=0
4)
将pi插入优先队列VT-label中
5)
Vgene(vi)={v∞},Vpred(vi)={v0},dgene(vi)=∞
6)
end for
7)
VP-label=∅
8)
whileVT-label≠∅ do
9)
【英国《国际核工程》网站2018年10月2日报道】 俄罗斯核燃料产供集团(TVEL)主管科技工作的副总裁亚历山大·乌格尔耶莫夫2018年9月27日宣布,产供集团计划与俄罗斯原子能工业公司(Rosenergoatom)达成协议,近期在VVER-1000反应堆中对耐事故燃料元件进行辐照试验。但没有指明具体将对哪种耐事故燃料进行辐照试验。
得到VT-label中最小顶点vmin,将vmin加入到VP-label
10)
将vmin从优先队列VT-label中去掉
11)
forvk∈Vadja(vmin) do
12)
D=dgene(vmin)+dS(vmin,vk)
13)
ifdgene(vk)=∞ do
Vgene(vk)={vmin},Vpred(vk)={vmin},dgene(vk)=D
15)
将vk插入优先队列VT-label中
16)
end if
17)
ifdgene(vk)>D对vk更新 do
18)
Vgene(vk)={vmin},Vpred(vk)={vmin},dgene(vk)=D
19)
将vk插入优先队列VT-label中
20)
end if
21)
ifdgene(vk)=D对vk更新do
22)
Vgene(vk)=Vgene(vk)∪Vgene(vmin)
23)
Vpred(vk)=Vpred(vk)∪{vmin},dgene(vk)=D
24)
将vk插入优先队列VT-label中
25)
end if
26)
end for
27)
end while
3.2 查询阶段
根据查询过程中节点vi到达时间AT(vpi,vpi+1,ti),动态选择AT(vpi,vpi+1,ti)所在时段对应的Gmin中节点vi的最近邻和到达最近邻的代价minc(vi,vj)作启发值。当查询点q在t时刻发起查询,假设t∈(ti,ti+1]。计算q到邻接点vi的到达时间AT(q,vi,t),确定AT(q,vi,t)所在的时段,假设AT(q,vi,t)∈(ti+1,ti+2],利用时段(ti+1,ti+2]所构建的Gmin在预处理阶段得到vi的最近邻及到达最近邻的代价min(TT(ti+1,ti+2]),令L=c(q,vi,t)+min(TT(ti+1,tt+2])作为评价函数,选取L值最小的节点vj继续扩展vj的邻接点,直到找到K近邻,ITD-FTT查询算法如算法2所示。
算法2 ITD-FTT查询算法。
输入:查找的近邻个数K,发起查询时间starttime,查询点q。
输出:含有K个最近邻的结果集NN。
1)
for 查询点q的邻接点vkdo
2)
TT(vk)=c(q,vk,starttime),
AT(vk)=TT(vk)+starttime
3)
匹配AT(vk)所在时段,根据所在时段对应的Gmin中预计算得到的vk最近邻及到达最近邻所需的时间:MinTime=Match(AT(vk))
4)
计算L=TT(vk)+MinTime
5)
在优先队列TList中加入vk
6)
end for
7)
while 结果集列表NN长度小于Kdo
8)
从TList中得到L值最小的节点vmin
9)
forvmin的邻接点vtdo
10)
TT(vi)=c(q,vi),AT(vi)=TT(vi)+TT(vmin)
11)
匹配AT(vi)所在时段,根据所在时段,根据所在时段对应的Gmin中预计算得到vi最近邻及到达最近邻所需的时间MinTime=Match(AT(vi))
12)
计算启发值L=TT(vi)+MinTime
13)
如果vi在TList中,且L值小于原有L值,则更新vi,并将更新后的vi加入到TList
14)
IfTT(vi)=L且vi为兴趣点
15)
将vi加入到结果集NN中
16)
end if
17)
end for
18)
end while
19)
returnNN
3.3 ITD-FTT算法实例说明
如图3,当t=8时,TD-FTT算法无法求解,下面利用ITD-FTT算法给出求解过程。令查询点q=a,查询时间t=8,K=2。遍历查询点a的邻接点{b,p2,c}并将a加入到队列VP-label。分别计算各节点的AT、TT、L值,并将节点加入到优先队列VT-label中。例如对于节点b,通过a到b的权值函数得TTb=c(a,b,8)=4.4,ATb=t+TTb=12.4,根据节点的到达时间判断节点所选择的预处理信息。因为ATb∈(10,20],因此选择GMIN(10,20],即表2的信息。由表2可知b的最近邻为p1且time1=6.5,所以启发值L=TTb+time1=10.9。得到的VT-label集合如下:{(TTb=4.4,ATb=12.4,Lb=10.9),(TTp2=9.4,ATp2=17.4,Lp2=9.4),(TTc=5.2,ATc=13.2,Lc=9.4)},选择启发值L最小的节点继续扩展,因此在VT-label中对节点c进行出队列操作同时在VP-label中加入c。与节点c相连的节点为p1,p3,操作如上,得到VP-label={a,c},VT-label集合如下:{(TTp2=9.4,ATp2=17.4,Lp2=9.4),(TTp3=9.84,ATp3=17.84,Lp3=9.84),(TTb=4.4,ATb=12.4,Lb=10.9),(TTp1=12.8,ATp1=20.8,Lp1=12.8)},接下来遍历L值最小的节点p2,因为p2为兴趣点且TT=L,该兴趣点为查找的目标节点。p2邻接点为p3,此时TTp3=14.7>9.84,因此,不更新p3的值。得到VP-label={a,p2,c},VT-label如下:{(TTp3=9.84,ATp3=17.84,Lp3=9.84),(TTb=4.4,ATb=12.4,Lb=10.9),(TTp1=12.8,ATp1=20.8,Lp1=12.8)},遍历节点p3,因为p3为兴趣点且TT=L,则该兴趣点为查找的目标节点,得到结果集NN={p3,p2}。在以上查询过程中启发值不受限于查询时刻所在的时段。
4 实验
4.1 实验参数
用德国奥尔登堡的路网图进行仿真实验,地图含节点6 105个,边7 035条。电脑配置处理器Inter Core i5- 3470 CPU @3.20 GHz,内存4 GB。根据实际路网变化规律。本文将全天分为5个时段,[22:00,7:00),[7:00,9:00),[9:00,17:00),[17:00,19:00),[19:00,22:00);每隔5 min对边赋权值,得到边的288个权值,根据边的权值拟合为分段线性函数。本文首先对TD-FTT和ITD-FTT算法在预处理阶段计算量进行对比实验。在查询阶段,将ITD-FTT算法同TD-INE(Time Dependent Incremental Network Expansion)算法[10],和将全天最小值作为启发值的TD-A(Time Dependent A star)算法进行对比验证其效率。
4.2 实验结果
4.2.1 预处理阶段实验
由于改进的算法只需求时段内静态路网中节点的最近邻,为与TD-FTT算发预处理阶段进行比较,因此令C=1,即假设TD-FTT算法在预处理过程中仅求解节点的最近邻。TD-FTT算法计算所有时段的平均预处理时间为3 052 ms,在ITD-FTT算法中利用NVD计算所有时段的最近邻所需时间为912 ms,时间减少了70.12%。因为,利用NVD可以并行计算所有节点的最近邻,因此,计算时间会大幅减少,并且,TD-FTT算法在计算过程中C>1,计算时间比C=1时增加,因此预处理阶段的改进使计算量大幅减少,改进效果明显。
4.2.2 查询阶段实验
对于查询处理阶段,实验对比不同算法的K值和兴趣点密度(Point Of Interest, POI)密度对查询响应时间和查询遍历节点的影响。令K的默认值为20,POI密度默认值设为0.1。
令K∈{1,5,10,15,20,25,30},对不同K值,随机进行30次查询。图4(a)比较了3种算法随K值增加查询响应时间的平均值对比曲线。图4(b)显示随K值增加查询遍历节点数的平均值对比曲线。可以看出,响应时间和遍历节点数随着K值的增加而增加,这是由于查询目标节点增加,需要扩展更多节点得到目标节点,而扩展节点的增加同时带来响应时间的增加。
ITD-FTT和TD-A算法比TD-INE算法平均遍历节点个数分别减少46.52%、35.73%,因为ITD-FTT和TD-A算法为启发式搜索算法,因此遍历节点个数比盲目扩展的TD-INE算法少。ITD-FTT比TD-A算法遍历节点个数减少了约16.63%,因为在同为启发搜索算法的前提下,ITD-FTT的启发值比TD-A更接近实际值,因此遍历节点个数更少,算法更高效。
ITD-FTT和TD-A算法的平均响应时间比TD-INE分别减少47.46%和35.73%,ITD-FTT比TD-A的响应时间减少约18.24%。因为响应时间的不同主要由遍历节点个数不同引起,因此响应时间随K值的变化趋势与遍历节点随K值的变化趋势相同。当K=1时,遍历的节点太少,所有算法的响应时间差距较小。
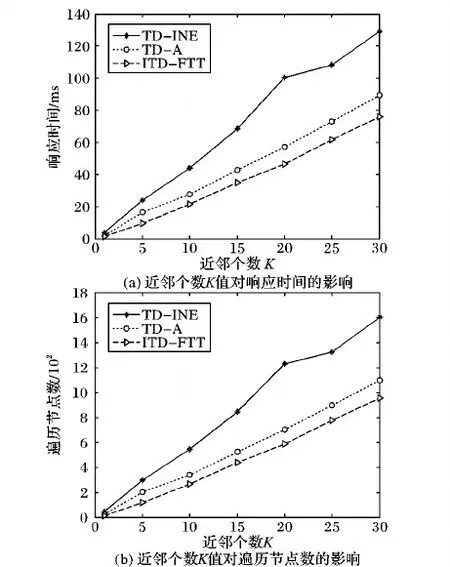
图4 K值对查询的影响
将POI的密度设置为5%、10%、15%、20%,在不同密度下,令K=20随机进行30次查询。图5(a)表示随POI密度的增加,查询响应时间的变化趋势。由图5(a)可知,随着密度的增加,3种算法的响应时间均在减少,但ITD-FTT算法的响应时间最少。图5(b)表示,随POI密度增加,查询遍历节点的变化规律。在图5(b)中,遍历节点的个数也随着密度的增大而减少,并且ITD-FTT算法所需遍历的节点数最少。
当查询目标节点个数K一定时,POI的密度增大,节点作为目标节点的概率增大,因此,随POI密度增大,遍历节点个数减少。又因为ITD-FTT和TD-A算法为启发式搜索算法,因此比盲目扩展的TD-INE算法遍历节点个数少,ITD-FTT、TD-A算法在同为启发搜索算法的前提下,ITD-FTT的启发值比TD-A更接近实际值,因此遍历节点个数减少,算法更高效。在3种算法中,ITD-FTT算法遍历的节点个数最少。由于响应时间由遍历节点个数决定且成同样趋势,因此,由遍历节点个数变化规律可知,响应时间也同样随POI密度增加而减少。
由以上分析结果可知,本文所提的ITD-FTT算法在响应时间和遍历节点个数上相比其他两种算法均有优势,并且在密度相同的情况下,响应时间和遍历节点个数的值均为最小。
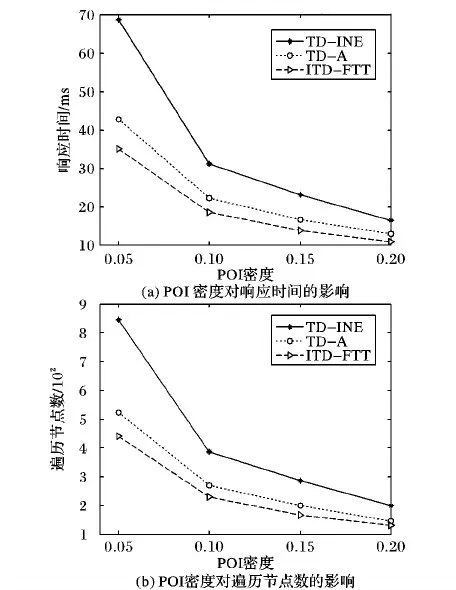
图5 POI密度对查询的影响
5 结语
与静态路网相比,时间依赖路网在位置广告、智能导航、紧急救援更具有现实意义。本文在不改变TD-FTT算法效率的前提下,在预处理阶段利用NVD并行计算节点的最近邻,减少预计算的计算量;在查询阶段根据节点到达时间所在的时段,动态选择启发值,避免利用查询时刻所在时段的最小值作启发值带来的不能跨时段查询的问题。通过仿真实验表明,ITD-FTT算法在预处理阶段计算量大幅度减少且查询阶段在响应时间和遍历节点个数上优于TD-INE算法和TD-A算法。将该方法利用在时间依赖路网的连续K近邻查询算法中,可作为进一步研究工作。
References)
[1] 廖巍,吴晓平,胡卫,等.基于最短路径的道路网络K近邻查询处理[J].计算机科学,2010,37(11):180-183.(LIAO W, WU X P, HU W, et al. Processing ofKnearest neighbor queries based on shortest path in road networks [J]. Computer Science, 2010, 37(11): 180-183.)
[2] 刘德高,李晓宇.基于路网的连续K近邻查询算法[J].计算机应用,2013,33(7):1964-1968.(LIU D G, LI X Y. ContinuousKnearest neighbor query algorithm based on road network [J]. Journal of Computer Applications, 2013, 33(7): 1964-1968.)
[3] 赵亮,陈荦,景宁,等.道路网中的移动对象连续K近邻查询[J].计算机学报,2010,33(8):1396-1404.(ZHAO L, CHEN L, JING N, et al. ContinuousKneighbor queriers of moving objects in road networks [J]. Chinese Journal of Computers, 2010, 33(8): 1396-1404.)
[4] KOLAHDOUZAN M, SHAHABI C. Voronoi-basedknearest neighbor search for spatial network databases [C]// VLDB 2004: Proceedings of the Thirtieth International Conference on Very Large Data Bases. San Francisco, CA: Morgan Kaufmann, 2004: 840-851.
[5] PAPADIAS D, ZHANG J, MAMOULIS N, et al. Query processing in spatial network databases [C]// VLDB 2003: Proceedings of the 29th International Conference on Very Large Data Bases. San Francisco, CA: Morgan Kaufmann, 2003: 802-813.
[6] HUANG X, JENSEN CS,ALTENIS S. The islands approach to nearest neighbor querying in spatial networks [C]// SSTD 2005: Proceedings of the 2005 International Symposium on Spatial and Temporal Databases. Berlin: Springer, 2005: 73-90
[7] ZHANG D, CHOW C-Y, LI Q, et al. SMashQ: spatial mashup framework fork-NN queries in time-dependent road networks [J]. Distributed and Parallel Databases, 2013, 31(2): 259-287.
[8] COSTA C F, NASCIMENTO M A, DEMACDO J A F, et al. A*-based solutions forkNN queries with operating time constraints in time-dependent road networks [C]// MDM 2014: Proceedings of the 2014 IEEE 15th International Conference on Mobile Data Management. Piscataway, NJ: IEEE, 2014: 23-32.
[9] ABEYWICKRAMA T, CHEEMA M A. Efficient landmark-based candidate generation forkNN queries on road networks [C]// DASFAA 2017: Proceedings of the 22nd Internation Conference on Database Systems for Advanced Applications. Berlin: Springer, 2017: 425-440.
[10] DEMIRYUREK U, BANAEI-KASHANI F, SHAHABI C. Efficientk-nearest neighbor search in time-dependent spatial networks [C]// DEXA 2010: Proceedings of the 2010 International Conference on Database and Expert Systems Applications. Berlin: Springer, 2010: 432-449.
[11] CRUZ L A, NASCIMENTO M A, MACEDO J A F.k-nearest neighbors queries in time-dependent road networks [J]. Journal of Information & Data Management, 2012, 3(3): 211-216.
[12] KOMAI Y, NGUYEN D H, HARA T, et al.kNN search utilizing index of the minimum road travel time in time-dependent road networks [J]. Information Sciences, 2014, 255(1): 135-154.
[13] 谭国真,高文.时间依赖的网络中最小时间路径算法[J].计算机学报,2002,25(2):165-172.(TAN G Z, GAO W. Shortest path algorithm in time-dependent networks [J]. Chinese Journal of Computers, 2002, 25(2): 165-172.)
[14] OKABE A, SATOH T, FURUTA T, et al. Generalized network Voronoi diagrams: concepts, computational methods, and applications [J]. International Journal of Geographical Information Science, 2008, 22(9): 965-994.
This work is partially supported by National Natural Science Foundation of China (61502317).
LIJiajia, born in 1987, Ph. D., lecturer. Her research interests include temporal data management, intelligent transportation.
LIUXiaojing, born in 1991, M. S. candidate. Her research interests include temporal data management.
LIUXiangyu, born in 1981, Ph. D., lecturer. His research interests include social network, privacy preserving.
XIAXiufeng, born in 1964, Ph. D., professor. His research interests include data warehouse, NoSQL database.
ZHURui, born in 1982, Ph. D., lecturer. His research interests include data stream management, spatiotemporal crowdsourcing.
