基于随机游走的多目标A*算法的改进

刘浩翰，郭晶晶，李建伏，贺怀清

(中国民航大学 计算机科学与技术学院，天津 300300)(*通信作者电子邮箱peony_g@163.com)

0 引言

目前很多研究领域的问题都可以归结为多目标最短路径问题，例如，车道规划、城市交通网络、机器人监控、卫星定位、路由通信网络等。

多目标最短路径问题是根据多个目标在图中找到起始节点到一个目的节点(一对一问题)或图中的多个节点(一对多问题)的所有帕累托(Pareto)最优解的集合。学者们提出了几种解决该问题的方法，包括枚举方法(标签设置[1]和标签校正[2])、排序算法[3]和两阶段算法[4]。在大规模图中，寻找任意给定的起始节点和目的节点间的最短路径(一对一的问题，例如路线图中的导航查询)，标签设置算法通常是最佳的选择。通常情况下，多目标标签设置算法是在单目标算法，如Dijkstra算法和A*算法[5]基础上改进的。在一对一问题中A*算法作为Dijkstra算法的变体，通过使用启发函数来提高搜索效率。如果启发函数值满足下界条件，则A*算法是一种精确的算法，即它总是返回一个最优解。极端情况下，如果启发函数值等于0，A*算法等同于Dijkstra算法。

1 相关知识

1.1 多目标A*算法

多目标A*算法描述如下：G=(N,A,c)用于表示描述搜索空间的有向图。其中：N表示节点，A表示两节点之间的有向弧，c表示标志有向弧的多目标代价向量，每一维代表一个目标。在G上任意指定起始节点s∈N，目的节点t∈N，寻找两节点间的非支配路径P=(n1,n2,…,nk)，代价向量c(P)可以通过路径的子部分的代价向量求和得到。多目标A*算法用到的部分重要定义如下。

定义1 支配()或帕累托最优偏序的定义如下：

∀y′,y∈Rqyy′ ⟺ ∀

其中，q是多目标问题中目标的个数。

定义2 词典顺序(L)的定义如下：

∀y′,y∈RqyLy′ ⟺ ∃∀

定义3 给定一个向量v=(v1,v2,…,vn)，它的截断向量t(v)为删除头元素的向量t(v)=(v2,v3,…,vn)。

定义4 给定一组向量X，关于它的截断向量为T(X)=nd({t(x)|x∈X})，T(X)里仅包括非支配向量。

1)初始化。起始节点s的标签Gop(s)={(0)}、Gcl(s)=∅，OPEN={(s,0,hs)}，COSTS=∅，两个截断向量集合T(Gcl(s))=∅和T(COSTS)=∅。

2)判断终止。如果OPEN为空，那么从当前节点回溯到起始节点，然后返回完整的路径，并且从COSTS中得到路径代价。

3)路径选择。如果OPEN不为空，从OPEN中选择一个标签(n,gn,fn)，其中的fn必须为f中非支配的，即∀(n′,gn′,fn′)∈OPEN，不存在fn′fn，并从OPEN中删除标签(n,gn,fn)，将gn从Gop(n)移入Gcl(n)，将t(gn)加入T(Gop(n))并更新T(Gcl(n))。如果Pareto过滤fn，则重复步骤3)。

4)路径(解)记录。如果节点n是目标节点，则将gn放入集合COSTS中，并将t(gn)放入T(COSTS)并且更新T(COSTS)。转向步骤3)。

5)扩展路径。如果节点n不是目标节点，则对节点n的所有子节点m进行如下操作。

①计算到节点m的路径的代价和其下限，gm=gn+c(n,m)和fm=gm+hm。

②如果不Pareto过滤fm：

如果m是被扩展出的新节点，则Gop(m)={(gm)}并且将(m,gm,fm)放入OPEN表中，并添加从n到m的指针；

如果g(m)等于Gop(m)∪Gop(m)中某向量，则添加从n到m的指针；

如果不进行Pareto修剪：从Gop(m)中删除所有被gm支配的gm′(gmgm′)，并在OPEN中删除相应的标签(m′,gm′,fm′)，将标签(m,gm,fm)放入OPEN表中，gm放入Gop(m)中并添加从n到m的指针。

③返回步骤3)。

1.2 随机游走策略

蒙特卡罗随机游走搜索使用随机游走策略跳跃搜索当前状态的一个邻接状态，重复循环直到搜索到目标状态。如果在经过m次这样的跳跃搜索后，所有状态的最小启发函数值仍然没有减小，或者遇到终端状态，蒙特卡罗随机游走会回到初始状态重新开始搜索。

随机游走搜索每次从一个状态开始搜索其邻接状态空间，试图找到一个具有更小启发式函数值的状态。在最多n次的循环中，每次搜索一条路径，计算每条路径末尾状态的启发式函数值，如果其值小于已搜索路径的最小值，则更新节点和节点的启发式函数值；最后返回具有最小启发式函数值的状态。

2.2 算法描述

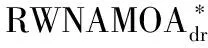
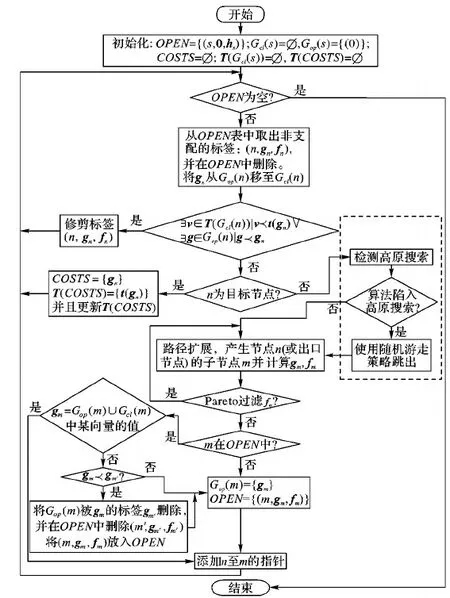
图算法流程

1)在扩展从OPEN表中选出的非支配标签之前，检测该标签是否属于高原搜索，若属于则退回至前m步的标签(s,gs,fs)。

2)从标签(s,gs,fs)开始，随机搜索t次，即算法不管是否找到一个更好的标签都将在有限的时间内返回一个标签。

3)每次随机搜索标签(s,gs,fs)的邻近长度为l的路径，并在n条路径中选择一条最好的路径(末尾标签的启发值h不被当前标签的启发值支配)，返回其末尾的标签；否则，该标签作为下一次游走的起始标签。在搜索过程中，当找到一个出口立刻返回，无需将n条路径全部搜索完后再结束。

3 实验分析

3.1 实验平台及环境

随机网格是评测多目标搜索算法的标准测试平台[20]。本文使用的随机网格允许解的长度控制算法性能的评估，具体是一张具有10 000个节点和39 800条弧的二维正方形网格图，并且其每个节点具有4个邻居节点。实验环境配置为：硬件环境为Intel Core i7- 6700 CPU@3.40 GHz,4 GB；操作系统为Windows 7 旗舰64位；编程软件为Lisp Works Professional 6.01；其他软件为Matlab 8.3。

实验将起始节点设置在网格的中心位置(50，50)。目的节点放置在中心节点至右下角节点的对角线上，使用解的长度d(20到100)表示目的节点的坐标(50+d/2，50+d/2)。网格中每条弧的代价向量c(i,j)=(c1,c2,c3)是使用均匀分布在1至10范围内产生的3个数。

3.2 实验结果与对比分析

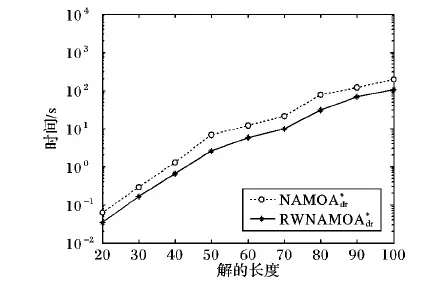
图2 多目标搜索算法的平均运行时间

鉴于此，可将其应用到空铁联运路径搜索问题中。空铁联运是指航空运输与铁路运输之间协作的一种联合运输方式，参与者包括民航机场、航空公司、铁路系统等。该算法可搜索出满足旅客出行多种需求的路线，例如，距离最短、花费最少或者时间最短等，对进一步提高提供给旅客的服务质量，实现民航业客源的增长具有重要的意义。

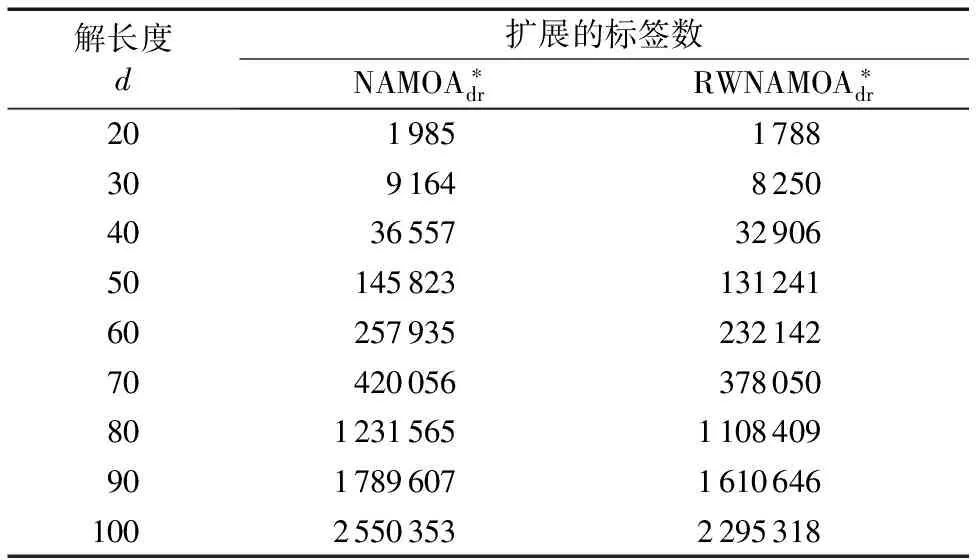
表1 两种算法的扩展标签平均数

4 结语

本文的研究和尝试仅仅是在多目标搜索问题的经典测试平台(随机网格)上进行的，后续工作还需要在真实的空铁联运网络中进行实验，以发现算法的适应性和局限性。另外，因为算法本质上是启发式搜索算法，启发函数对搜索起决定作用，算法应用于空铁联运时需要具体研究启发函数的设计和实现。

References)

[1] MANDOW L, PÉREZ de la CRUZ J. Path recovery in frontier search for multi-objective shortest path problems [J]. Journal of Intelligent Manufacturing, 2008, 21(1): 89-99.

[4] MOTE J, MURTHY I, OLSON D L. A parametric approach to solving bicriterion shortest path problems [J]. European Journal of Operational Research, 1991, 53(1): 81-92.

[5] HART P, NILSSON N, RAPHAEL B. A formal basis for the heuristic determination of minimum cost paths [J]. IEEE Transactions on Systems Science and Cybernetics, 1968, 4(2): 100-107.

[6] HANSEN P. Bicriterion path problems [C]// Proceedings of the Third Conference on Multiple Criteria Decision Making Theory and Application. Berlin: Springer, 1980: 109-127.

[7] STEWART B S, WHITE C C. Multi-objective A*[J]. Journal of the ACM, 1991, 38(4): 775-814.

[8] MANDOW L, PÉREZ de la CRUZ J L. Multi-objective A*search with consistent heuristics [J]. Journal of the ACM, 2010, 57(5): Article No. 27.

[9] PULIDO F J, MANDOW L, PÉREZ de la CRUZ J L. Dimensionality reduction in multi-objective shortest path search [J]. Computers & Operations Research, 2015, 64: 60-70.

[10] HAMPSON S, KIBLER D. Plateaus and plateau search in boolean satisfiability problems: when to give up searching and start again [C]// Proceedings of the 2nd DIMACS (Center for Discrete Mathematics and Theoretical Computer Science) Implementation Challenge, Cliques, Coloring and Satisfiability. Providence, RI: American Mathematical Society, 1993: 437-456.

[11] FRANK J D, CHEESEMAN P, STUTZ J. When gravity fails: local search topology [J]. Journal of Artificial Intelligence Research, 1997, 7(1): 249-281.

[12] HOFFMANN J. Local search topology in planning benchmarks: an empirical analysis [C]// IJCAI’01: Proceedings of the 17th International Joint Conference on Artificial Intelligence. San Francisco, CA: Morgan Kaufmann, 2001: 453-458.

[13] HOFFMANN J. Local search topology in planning benchmarks: a theoretical analysis [C]// Proceedings of the 2002 International Conference on AI Planning and Scheduling. Menlo Park, CA: AAAI Press, 2002: 92-100.

[14] BENTON J, TALAMADUPULA K, EYERICH P, et al. G-value plateaus: challenge for planning [C]// Proceedings of the Twentieth International Conference on Automated Planning and Scheduling. Menlo Park, CA: AAAI Press, 2010: 259-262.

[15] GOVER F, LAGUNA M. Tabu Search*[M]. Norwell, MA: Kluwer Academic Publishers, 2013: 3261-3362.

[16] KAUTZ H, SELMAN B. Pushing the envelope: planning, propositional logic, and stochastic search [C]// AAAI’96: Proceedings of the Thirteenth National Conference on Artificial Intelligence. Menlo Park, CA: AAAI Press, 1996: 1194-1201.

[17] NAKHOST H, MÜLLER M. Monte-Carlo exploration for deterministic planning [C]// Proceedings of the Twenty-First International Joint Conference on Artificial Intelligence. Menlo Park, CA: AAAI Press, 2009: 1766-1771.

[18] NAKHOST H, HOFFMANN J, MÜLLER M. Resource-constrained planning: a Monte Carlo random walk approach [C]// Proceedings of the Twenty-Second International Conference on Automated Planning and Scheduling. Menlo Park, CA: AAAI Press, 2012: 181-189.

[19] 吕强.面向高性能和强表达力的自动规划[D].合肥：中国科学技术大学，2012:29-45.(LYU Q. Towards enhanced efficiency and expressiveness of automated planning [D]. Hefei: University of Science and Technology of China, 2012: 29-45.)

[20] MACHUCA E, MANDOW L, PÉREZ de la CRUZ J L, et al. A comparison of heuristic best-first algorithms for bicriterion shortest path problems [J]. European Journal of Operational Research, 2012, 217(1): 44-53.

This work is partially supported by the Tianjin Research Program of Application Foundation and Advanced Technology (14JCZDJC32500).

LIUHaohan, born in 1966, M. S., associate professor. His research interests include intelligent processing of civil aviation information.

GUOJingjing, born in 1988, M. S. candidate. Her research interests include intelligent processing of civil aviation information.

LIJianfu, born in 1979, Ph. D., associate professor. Her research interests include civil aviation information system, artificial intelligence.

HEHuaiqing, born in 1969, Ph. D., professor. Her research interests include data mining, graphic, image and visual analysis.